High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Addition and subtraction Place value Decimals Fractions Simplifying fractions Mixed number to improper fractionMultiplication
Here you will learn about multiplication, including multiplying multi-digit whole numbers, properties of multiplication, multiplying decimals, multiplying fractions, and multiplying integers.
Students will first learn about multiplication as part of operations and algebraic thinking in third grade.
What is multiplication?
Multiplication is a mathematical operation that involves combining groups of numbers together to find their total. For example, "3 \times 4" means 3 groups of 4, which equals 12. The numbers that are multiplied together are called factors and the answer is called the product.
When you write a multiplication equation, the first factor is called the multiplicand and the second factor is called the multiplier.
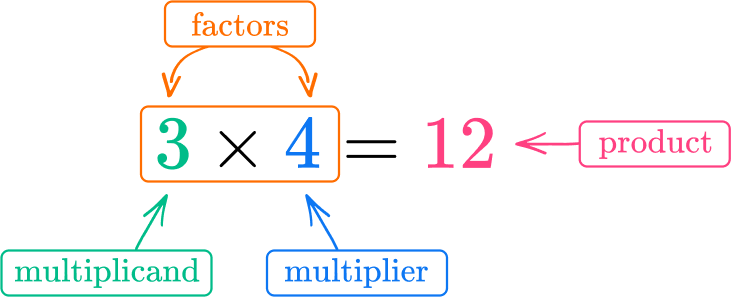
Multiplication can be thought of as a shortcut for repeated addition. Instead of adding a number to itself a certain number of times, we can use multiplication to find the total. For example, "3 \times 4" is the same as saying "4 + 4 + 4", which equals 12.
Look at the equal groups of triangles below.
There are 8 groups of triangles with 4 triangles in each group.
Instead of counting the number of triangles or adding 4 to itself 8 times, we can multiply to find the total more quickly.
8 groups of 4 = \; ?
8 \times 4=32There are 32 triangles altogether.

![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)
![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4th, 5th and 7th grade multiplication and division topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)
![[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)](https://thirdspacelearning.com/wp-content/uploads/2023/11/Multiplication-and-Division-Check-for-Understanding-listing-image.png)
Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4th, 5th and 7th grade multiplication and division topics to identify areas of strength and support!
DOWNLOAD FREEProperties of multiplication
The properties of multiplication are rules that always apply when multiplying numbers.
The 5 properties of multiplication are:
Commutative property of multiplication: This property says that the order of the factors in a multiplication equation does not change the product.
For any two numbers, a \times b=b \times a
Associative property of multiplication: This property says that the grouping of factors does not affect the product. In other words, when multiplying three or more numbers, you can regroup them in any way, and the result will remain the same.
For any three numbers, (a \times b) \times c=a \times(b \times c)
Distributive property of multiplication: This property says that when you multiply a number by a sum (or difference) of two numbers, you can distribute the multiplication across the terms inside the parentheses.
For any three numbers, a \times(b+c)=(a \times b)+(a \times c) \, or \, a \times(b-c)=(a \times b)-(a \times c)
Identity property of multiplication: This property says that any number multiplied by 1 equals the original number. For any number, a \times 1=a
Zero property of multiplication: This property says that any number multiplied by 0 equals 0. For any number, a \times 0=0
Multiplying multi-digit whole numbers
To multiply multi-digit whole numbers, you can use the area model or the standard algorithm, which is taught in 5 th grade.
- Area model: A rectangular model used to solve a multiplication problem where each factor is broken down by place value to make up the length and width of the rectangle.
Example: 42 \times 16 = \; ?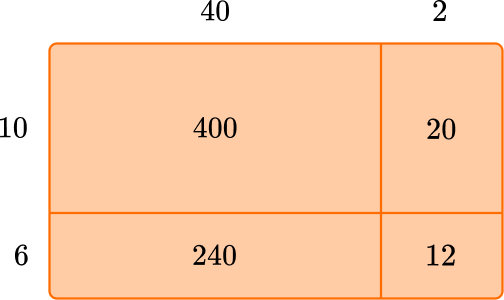
After multiplying the length and width of each section, you add up the partial products.
400 + 240 + 20 + 12 = 672
So 42 \times 16=672
- Standard algorithm: A step-by-step process used to multiply multi-digit numbers by breaking them down into smaller parts and then multiplying those parts separately.
You can multiply the same numbers using the standard algorithm.
42 \times 16 = \; ?
Using this method, the second number (16) is broken up and multiplied by the top number in parts. First, 6 is multiplied by 42, which gives a partial product of 252.
Then 10 is multiplied by 42 which gives a partial product of 420. The partial products are added together to get 672.
So 42 \times 16=672.
Multiplying decimals
Decimals can also be multiplied using the area model and the standard algorithm.
Example: 3.75 \times 9.8
- Area model
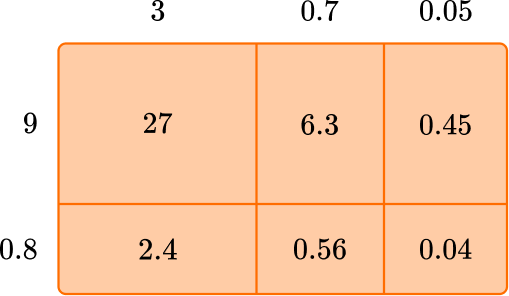
Then add up the partial products. To avoid a calculation error, add the top row, then the bottom row. Then add those totals together.
\begin{aligned} & 27+6.3+0.45=33.75 \\\\ & 2.4+0.56+0.04=3 \end{aligned}
33.75+3=36.75
So 3.75 \times 9.8=36.75.
- Standard algorithm:
When multiplying decimals using the standard algorithm, ignore the decimal points and set up the numbers as you would whole numbers. Unlike adding decimals, you do not line up the decimal points.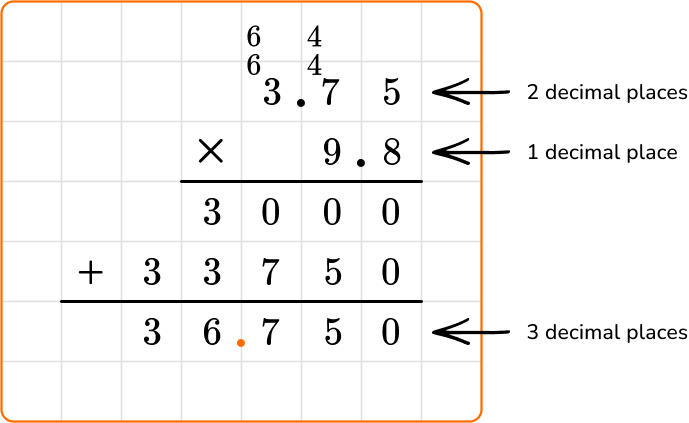
To determine where to put the decimal point in the product, add up the total number of decimal places (digits after the decimal point) between the two factors.
The first factor has 2 decimal places and the second factor has 1, giving a total of 3 decimal places. So the product will have 3 decimal places (3 digits after the decimal point ).
Multiplying fractions
To multiply fractions, multiply the numerators together and the denominators together.
Example: \cfrac{4}{5} \times \cfrac{1}{3}=\cfrac{4}{15}
To multiply mixed numbers, convert to an improper fraction first, then multiply the numerators and denominators together. Then simplify your answer.
Example:
\begin{aligned} & 1 \cfrac{2}{3} \times 2 \cfrac{1}{4} \\\\ & \; \downarrow \quad \, \downarrow \\\\ & \; \cfrac{5}{3} \times \cfrac{9}{4}=\frac{45}{12} \end{aligned}
\cfrac{45}{12} simplifies to \cfrac{15}{4} , then finally to 3 \cfrac{3}{4} .
So 1 \cfrac{2}{3} \times 2 \cfrac{1}{4}=3 \cfrac{3}{4} .
Multiplying integers
Positive integer \times negative integer
- Multiplying a positive integer by a negative integer will always result in a negative integer
- Example: 5 \times(-3)=-15
Positive integer \times positive integer
- Multiplying a positive integer by a positive integer will always result in a positive integer
- Example: 5 \times 3=15
Negative integer \times negative integer
- Multiplying a negative integer by a negative integer will always result in a negative integer
- Example: (-5) \times(-3)=15
What is multiplication?

Common Core State Standards
How does this relate to 3 rd grade math through 7 th grade math?
- Grade 3 – Operations and Algebraic Thinking (3.OA.A.1)
Interpret products of whole numbers, e.g., interpret 5 \times 7 as the total number of objects in 5 groups of 7 objects each. For example, describe a context in which a total number of objects can be expressed as 5 \times 7.
- Grade 3 – Operations and Algebraic Thinking (3.OA.A.3)
Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Grade 3 – Operations and Algebraic Thinking (3.OA.B.5)
Apply properties of operations as strategies to multiply and divide. Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication.)
3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication.)
Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property.)
- Grade 3 – Operations and Algebraic Thinking (3.OA.C.7)
Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division ( e.g., knowing that 8 \times 5 = 40, one knows 40 \div 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
- Grade 3 – Number and Operations in Base Ten (3.NBT.A.1)
Multiply one-digit whole numbers by multiples of 10 in the range 10–90 ( e.g., 9 \times 80, 5 \times 60) using strategies based on place value and properties of operations.
- Grade 4 – Operations and Algebraic Thinking (4.OA.A.1)
Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 \times 7 as a statement that 35 is 5 times as many as 7 and 7 times as many as 5. Represent verbal statements of multiplicative comparisons as multiplication equations.
- Grade 4 – Operations and Algebraic Thinking (4.OA.A.2)
Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
- Grade 4 – Number and Operations in Base Ten (4.NBT.B.5)
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
- Grade 4 – Number and Operations—Fractions (4.NF.B.4)
Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
- Grade 5 – Number and Operations in Base Ten (5.NBT.B.5)
Fluently multiply multi-digit whole numbers using the standard algorithm.
- Grade 5 – Number and Operations in Base Ten (5.NBT.B.7)
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
- Grade 5 – Number and Operations—Fractions (5.NF.B.4)
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
- Grade 5 – Number and Operations—Fractions (5.NF.B.6)
Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
- Grade 6 – The Number System (6.NS.B.3)
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
- Grade 7 – The Number System (7.NS.A.2)
Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers.
How to multiply
In order to use multiplication to find the total number of objects in equal groups:
- Count the number of groups.
- Count the number of objects in each group.
- Multiply the two numbers.
In order to use multiply multi-digit whole numbers and decimals:
- Write the multiplication equation.
- Choose a strategy to solve.
- Solve the equation.
In order to use multiply fractions:
- If either fraction is a mixed number, convert it to an improper fraction.
- Multiply the numerators.
- Multiply the denominators.
- Simplify if possible.
In order to use multiply integers:
- Multiply the two numbers and look at their signs. If the integers have the same sign, the product is positive. If not, go to step \bf{2}.
- If the integers have different signs, the product is negative.
- Write the correct sign on the product.
Multiplication examples
Example 1: equal groups
Find the total number of circles.
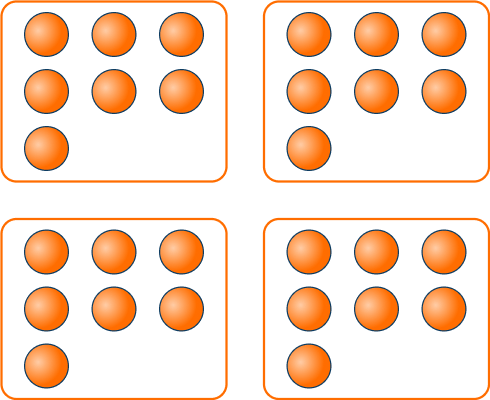
- Count the number of groups.
There are 4 groups.
2Count the number of objects in each group.
There are 7 circles in each group.
3Multiply the two numbers.
4 \times 7=28There are a total of 28 circles.
Example 2: area model (whole numbers)
Solve 25 \times 19.
Write the multiplication equation.
Choose a strategy to solve.
You can use the area model to solve. To set it up, draw a rectangle and split it into 2 rows and 2 columns since you need to multiply two 2- digit numbers.
Then decompose each number into tens and ones as shown below.
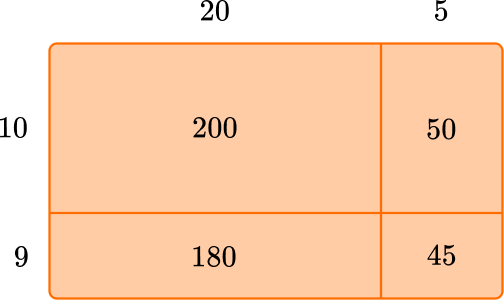
After multiplying each part, add up the partial products:
200 + 50 + 180 + 45 = 475
Solve the equation.
Example 3: standard algorithm (whole numbers)
Solve 3,198 \times 14.
Write the multiplication equation.
Choose a strategy to solve.
Larger numbers are typically multiplied using the standard algorithm.
To set it up, stack the numbers with the larger number on top and, since they are whole numbers, you can align the place values.
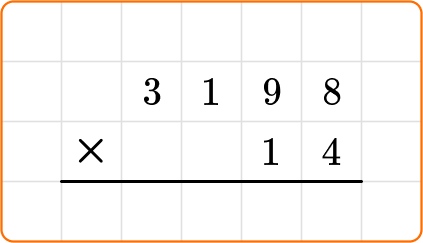
Then begin the process by multiplying one part at a time.

Solve the equation.
Example 4: area model (decimals)
Solve 8.5 \times 0.32
Write the multiplication equation.
Choose a strategy to solve.
The area model (similar to the area model used above for whole numbers) can be used to break apart each number and multiply it in parts.
To set it up, draw a rectangle and split it into 1 row and 3 columns since you need to multiply a 1- digit number by a 3- digit number.
Then decompose each number into its place values, as shown below.

After multiplying each part, add up the partial products:
54 + 3.6 + 0.72 = 58.32
Solve the equation.
Example 5: standard algorithm (decimals)
Solve 85 \times 2.97 = \; ?
Write the multiplication equation.
Choose a strategy to solve.
You can use the standard algorithm to solve. Stack the numbers the same way you would if they were whole numbers, but this time the number with the most digits (not necessarily the larger number) will go on top.
You will not align place values or the decimal point.
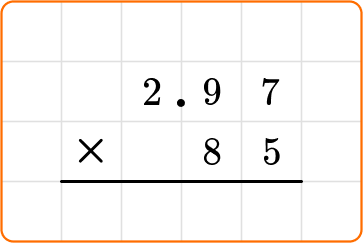
Then you can begin the multiplication process.
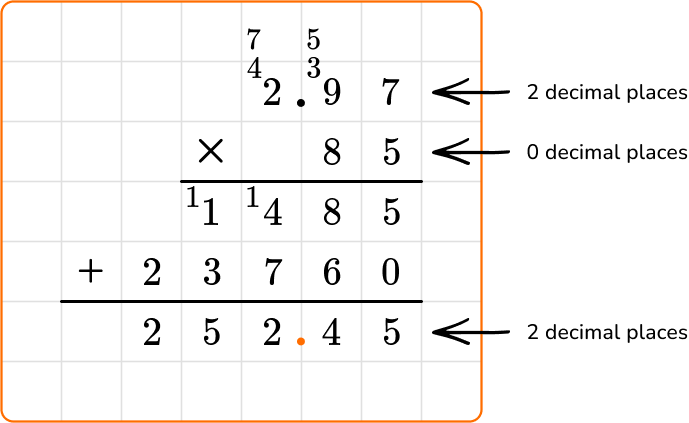
Count the number of decimal places in the factors. Since there are 2 altogether, there will be 2 decimal places in the product.
Solve the equation.
Example 6: fractions
Solve \cfrac{5}{8} \times \cfrac{3}{4}=
If either fraction is a mixed number, convert it to an improper fraction.
Neither of the fractions is a mixed number.
Multiply the numerators.
Multiply the denominators.
Simplify if possible.
\cfrac{15}{32} is in simplest form.
Example 7: mixed numbers
Solve 2 \cfrac{1}{6} \times \cfrac{2}{3}=
If either fraction is a mixed number, convert it to an improper fraction.
So the new equation is \cfrac{13}{6} \times \cfrac{2}{3}=
Multiply the numerators.
Multiply the denominators.
Simplify if possible.
\cfrac{26}{18} can be simplified to \cfrac{13}{9} and then further simplified to 1 \cfrac{4}{9}.
Example 8: integers
Solve -8 \times 7 .
Multiply the two numbers and look at their signs. If the integers have the same sign, the product is positive. If not, go to step \bf{2}.
Recalling your multiplication facts, you should know that 8 \times 7=56.
In the equation -8 \times 7, the numbers have different signs. –8 is a negative number and 7 is a positive number.
If the integers have different signs, the product is negative.
In the equation -8 \times 7, the numbers have different signs.
Write the correct sign on the product.
The product is –56.
Teaching tips for multiplication
- Practice multiplication tables regularly. Encourage learners to memorize multiplication facts through drills and multiplication games and not just on worksheets. Flashcards and interactive apps can also be helpful tools.
- Incorporate visual aids such as arrays, diagrams, number lines, or manipulatives like counting blocks or beads to help students visualize basic multiplication as combining equal groups.
- Integrate math games and puzzles into your lessons to make learning multiplication more fun and engaging.
- Allow students to build a foundational understanding of basic multiplication before introducing strategies to use for multi-digit multiplication.
Easy mistakes to make
- Memorizing without understanding
Students can have their multiplication facts memorized, but without the foundational understanding of multiplication, these are meaningless.
- Errors in carrying or regrouping
When using the standard algorithm for multiplication, students may make mistakes in carrying over or regrouping digits, especially with larger numbers.
- Forgetting the properties of multiplication
Each property can assist students when solving multiplication equations. If students forget these, it can lead to mistakes in calculations or unnecessary extra steps.
Related multiplication and division lessons
Practice multiplication questions
1. Which multiplication equation represents the total number of stars?





There are 9 groups with 5 starts in each group. This can be written as 9 \times 5 which equals 45.
2. Solve 652 \times 31 using any strategy.




Students can multiply multi-digit whole numbers using any strategy, such as an area model or the standard algorithm.
Here is an example of this equation being solved via the standard algorithm:
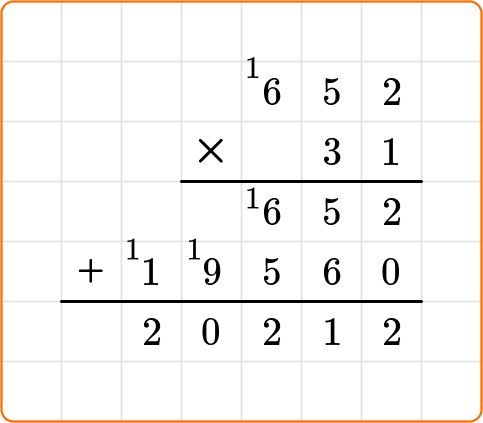
3. Solve 91.2 \times 0.7 using any strategy.




Students can multiply decimals using any strategy, such as an area model or the standard algorithm.
Here is an example of this equation being solved via the area model:

63+0.7+0.14=63.84
4. Solve \cfrac{9}{10} \times \cfrac{3}{5} and simplify your answer.




To solve, simply multiply the two numerators, then multiply the two denominators.
\cfrac{9}{10} \times \cfrac{3}{5}=\cfrac{27}{50}
Since 27 and 50 have no common factors, this fraction is in its simplest form.
5. Solve 5 \cfrac{2}{7} \times 3 \cfrac{1}{2} and simplify your answer.




To multiply mixed numbers, first the mixed numbers need to be converted to improper fractions. Then you can multiply the numerators and multiply the denominators before simplifying your answer.
\begin{aligned} & 5 \cfrac{2}{7} \times 3 \cfrac{1}{2}= \\\\ & \; \downarrow \quad \, \downarrow \\\\ & \cfrac{37}{7} \times \frac{7}{2}=\cfrac{259}{14} \end{aligned}
\cfrac{259}{14} simplifies to \cfrac{37}{2} then again to 18 \cfrac{1}{2}.
6. (-6) \times(-7) = \; ?




The product of 2 negative numbers is always positive.
So (–6) × (–7) = 42
Multiplication FAQs
Multiplication is one of the four basic arithmetic operations. It involves combining or adding a number multiple times.
Times tables are a set of numbers arranged in a grid or chart that shows the results of multiplying numbers from 1 to 10 (or more) together. They help us quickly find the answers to multiplication problems.
The standard algorithm for multiplication is a step-by-step process used to multiply multi-digit numbers. It involves breaking down the multiplication problem into smaller, easier-to-solve parts and then combining the results (the partial products) to find the final answer.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!