High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Adding decimals Subtracting decimals Multiplying decimals Dividing decimalsMoney word problems
Here you will learn about money word problems, including the values of the coins in our money system and solving a variety of money word problems.
Students will first learn about money word problems as part of measurement and data in 2nd grade and continue to build on this knowledge as they learn how to operate with decimals as a part of numbers and operations in base 10 in 5th grade.
What are money word problems?
Money word problems use US money in cents (¢) and dollars (\$).
To solve money word problems, you need to know the names and values of the coins and bills in our money system.

There are also bills for different dollar amounts. The first four bills are…
\$1.00 (one dollar) | \$5.00 (five dollar) |
\$10.00 (ten dollar) | \$20.00 (twenty dollar) |
For example,
Solving in cents \textbf{(¢)} :
Jesse has 4 pennies, 3 nickels and 2 dimes. How many cents does Jesse have in total?
4 pennies = 4¢
3 nickels = 15¢
2 dimes = 20¢
4 + 15 + 20 = 39So Jesse has 39¢.
Solving in dollars \bf{(\$)} :
A pair of shoes costs \$22.45. Joe buys 3 pairs of them, how much will the 3 pairs cost?
\$22.45 \times 3 = \$22.45 + \$22.45 + \$22.45= 66 wholes, 12 tenths, and 15 hundredths.
= \$67.35The 3 pairs cost \$67.35.
What are money word problems?
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
[FREE] Arithmetic Worksheet (Grade 4 to 6)
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of arithmetic. 10+ questions with answers covering a range of 4th, 5th and 6th grade arithmetic topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
[FREE] Arithmetic Worksheet (Grade 4 to 6)
![[FREE] Arithmetic Worksheet (Grade 4 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Arithmetic-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 4 to 6 students’ understanding of arithmetic. 10+ questions with answers covering a range of 4th, 5th and 6th grade arithmetic topics to identify areas of strength and support!
DOWNLOAD FREECommon Core State Standards
How does this relate to 2nd grade math and 5th grade math?
- Grade 2 – Measurement and Data (2.MD.C.8)
Solve word problems involving dollar bills, quarters, dimes, nickels, and pennies, using \$ and ¢ symbols appropriately. Example: If you have 2 dimes and 3 pennies, how many cents do you have?
- Grade 5 – Numbers and Operations in Base 10 (5.NBT.B.7)
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
How to solve money word problems
In order to solve money word problems in cents:
- Recall the value of each coin.
- Find the total for each type of coin.
- Add all total coin values.
- Write a sentence answering the money word problem question.
In order to solve money word problems in dollars:
- Read the question carefully and decide which operation(s) to use.
- Use what you know about decimals to solve.
- Write a sentence answering the money word problem question.
Money word problems examples
Example 1: whole number word problem – adding coins
Mark has 12 pennies and 5 nickels. How many cents does he have?
- Recall the value of each coin.
Each penny is 1¢. Each nickel is 5¢.
2Find the total for each type of coin.
12 pennies = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 12¢
5 nickels = 5 + 5 + 5 + 5 + 5 = 25¢
3Add all total coin values.
12¢ + 25¢ = 37¢4Write a sentence answering the money word problem question.
Mark has 37¢.
Example 2: whole number word problem – adding coins
A pencil costs 3 dimes and 2 quarters. How many cents does the fancy pencil cost?
Each dime is 10¢. Each quarter is 25¢.
3 dimes = 10 + 10 + 10 = 30¢
2 quarters = 25 + 25 = 50¢
A fancy pencil costs 80¢.
Example 3: whole number word problem – subtracting coins
Kia has 3 quarters. A piece of gum costs 6 nickels. If Kia buys one piece of gum, how many cents will she have left?
Each nickel is 5¢. Each quarter is 25¢.
6 nickels = 5 + 5 + 5 + 5 + 5 + 5 = 30¢
3 quarters = 25 + 25 + 25 = 75¢
Kia will have 45¢ after buying one piece of gum.
Example 4: decimal word problem – one step addition
Hank buys a bottle of water for \$1.95 and a sandwich for \$4.56. How much did he pay in total?
You need to add to find the total of the water and the sandwich together.
1.95 + 4.56 =
One way to solve with decimals is to use what you know about fraction addition.
1.95=1 \cfrac{95}{100} \quad and \quad 4.56=4 \cfrac{56}{100}
\begin{aligned}
& 1 \cfrac{95}{100}+4 \cfrac{56}{100} \\\\
& = 5+\cfrac{151}{100} \\\\
& = 5+\cfrac{100}{100}+\cfrac{51}{100} \\\\
& = 5+1+\cfrac{51}{100} \\\\
& = 6 \cfrac{51}{100} \\\\
& = 6.51
\end{aligned}
Hank paid \$6.51 for the bottle of water and sandwich.
Example 5: decimal word problem – one step division
Two boxes of markers cost \$8.28. If each box costs the same, how much does one box of markers cost?
You need to take the total cost and divide it between the two boxes.
8.28 \div 2=
One way to solve with decimals is by breaking up the decimal into each place value.
8.28 \div 2=(8+0.2+0.08) \div 2=

8 \div 2=4
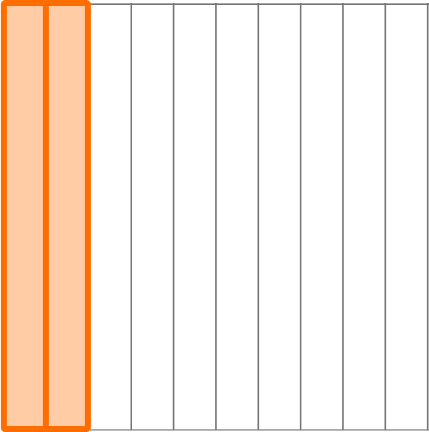
0.2 \div 2=0.1
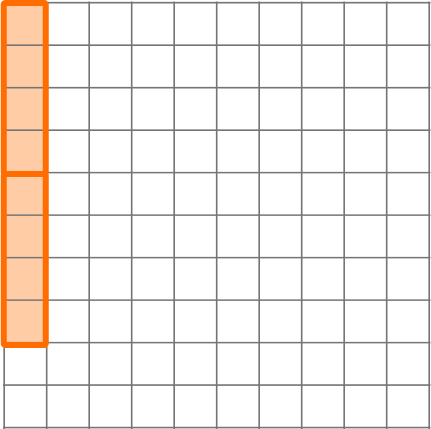
0.08 \div 2=0.04
Add the partial quotients:
4 + 0.1 + 0.04 = 4.14
Each box of markers cost \$4.14.
Example 6: decimal word problem – one step multiplication
Sara is saving to buy a science kit. She saves \$11.25 each week. How much money will she have saved after 5 weeks?
You need to multiply since she saved the same amount each week.
11.25 \times 5=
One way to solve with decimals is by breaking up the decimal into friendly numbers.
11.25 \times 5=(11+0.25) \times 5=
11 \times 5=55

Add the partial products:
55 + 1.25 = 56.25
After 5 weeks, Sara will have saved \$56.25.
Teaching tips for money word problems
- When first introducing 2nd graders to the money system, give them plenty of opportunities to use real life coins. This will help them memorize the value of each coin and also encourage solving by skip counting.
- Give 2nd graders experiences representing the same amount of money in different ways. For example, ask them, “How many different ways can you show 45 cents with coins?” This gives students practice memorizing the coin values and also encourages them to look for patterns.
- Solving money word problems can be difficult for students who have a lower reading comprehension. Provide visuals or phonics support to any student who may need it, so that their reading comprehension is not a barrier for this skill.
- Math worksheets, including money word problem worksheets, can be a good way for students to practice, but they should not be the only way that students learn this skill. Set up real-world scenarios in the classroom that involve solving with money, such as budgeting, to give students real life experiences connected to this skill.
- While you may introduce them separately, at some point it is necessary to combine practice with subtraction word problems and addition word problems so that students can practice figuring out which operation to use.
Easy mistakes to make
- Confusing the penny, dime and nickel coins
Without much experience using the coins, it is easy for students to confuse the values based on the size of the coin. The penny has the smallest value, but the dime coin is smaller in size. The dime coin is also smaller than the nickel, though the dime has more value.
For example, the first three coins from least to greatest value is (1¢, 5¢, 10¢) :

- Use two decimals places to record money in dollars
Always use two decimal places when writing the final amount of money in dollars.
For example, if your answer is 3.4, write it as \$3.40, using two decimal places to represent all the money positions.
- Subtracting from \bf{\$5, \$10} and so on
Finding the change from whole dollars can be tricky because of the zeros involved. You may wish to use a number line instead and count on.
For example, finding the change from \$10 for a \$3.72 shopping bill.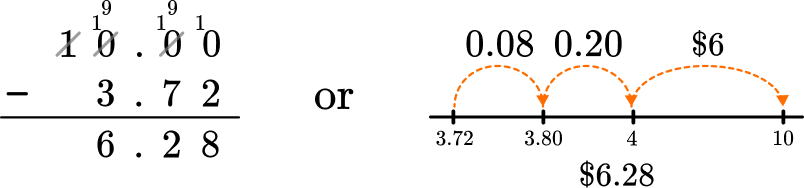
Related lessons on arithmetic
Practice money word problems questions
1. There are 3 dimes, 6 pennies and 4 nickels. How many cents are there?




Each penny is 1¢. Each nickel is 5¢. Each dime is 10¢.
6 pennies = 1 + 1 + 1 + 1 + 1 + 1 = 6¢
4 nickels = 5 + 5 + 5 + 5 = 20¢
3 dimes = 10 + 10 + 10 = 30¢
Add all total coin values.
6¢ + 20¢ + 30¢= 56¢
There is 56¢.
2. A bag of chips costs 75¢. Mark has 3 quarters and 17 pennies. If he buys a bag of chips, how many cents will he have left?




Each penny is 1¢. Each nickel is 25¢.
17 pennies = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 17¢
3 quarters = 25 + 25 + 25 = 75¢
Add all total coin values.
17¢ + 25¢ = 92¢
Subtract to find the cents he will have left.
92¢-75¢ = 17¢
Mark will have 17¢ left.
3. Maryam has 5 dimes and 3 pennies. Then she finds 2 nickels. How many cents does Maryam have now?




Each penny is 1¢. Each nickel is 5¢. Each dime is 10¢.
3 pennies = 1 + 1 + 1 = 3¢
2 nickels = 5 + 5 = 10¢
5 dimes = 10 + 10 + 10 + 10 + 10 = 50¢
Add all total coin values.
3¢ + 10¢ + 50¢= 63¢
Maryam now has 63¢.
4. Daniel buys a new pair of headphones for \$34.99. If he pays the cashier \$50, how much change will Daniel get back?




You need to subtract to find the difference between the money he gave the cashier and the cost of the headphones.
50.00-34.99 =
One way to solve with decimals is to use a number line.
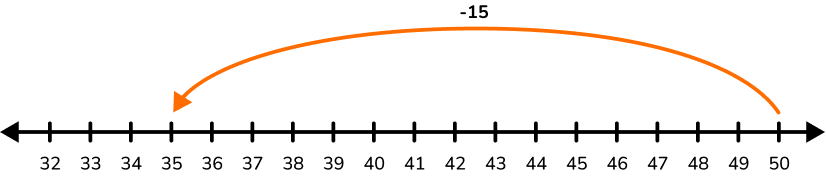
50-35= 15
From 35 to 34.99 is subtracting 0.01 more, so 50-34.99 = 15.01.
Daniel will get \$15.01 back.
5. A website charges \$9.99 a month to watch tv shows and movies. How much will 4 months cost?




You need to multiply to find the total price since each month is the same price.
9.99 \times 4 =
One way to solve with decimals is by breaking up the decimal into place values.
9.99 \times 4=(9+0.9+0.09) \times 4=
9 \times 4=36

0.9 \times 4=3.6

0.09 \times 4=0.36
Then combine each place value.
Whole numbers: 36 + 3 = 39
Tenths: 0.6 + 0.3 = 0.9
Hundredths: 0.06
Four months will cost \$39.96.
6. Maria had \$13.45 saved and then she was given \$23.50 on her birthday. How much money does she have now?




You need to combine the money she has saved and the money she was given, so add the numbers.
13.45 + 23.50 =
One way to solve with decimals is to use what you know about fraction addition.
13.45=13 \cfrac{45}{100} \quad and \quad 23.50=23 \cfrac{50}{100}
\begin{aligned} & 13 \cfrac{45}{100}+23 \cfrac{50}{100} \\\\ & =36+\cfrac{95}{100} \\\\ & =36 \cfrac{95}{100} \\\\ & =36.95 \end{aligned}
Maria has \$36.95 now.
Money word problems FAQs
In 5th grade, students operate with decimals using their own strategies based on place value understanding and the connection to whole number and fraction operations. 6th grade is when students learn the standard algorithm for decimal operations.
Because coins have the value of 1, 5, 10, and 25, learning to operate with the coins builds student understanding of not only the operations but of patterns in our Base 10 system. When students begin to solve in dollars, they deepen their understanding of operating with decimals.
Learning how to use the money system is an important life skill. As students get older they will encounter situations like calculating the total of a bill or making change, so it is important that they have classroom experiences that promote the understanding of our money system.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!