2. Which graph represents the graph of a system with no solution?

Systems of Equations - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Linear graphs Linear equations

Rearranging equations

Math resources Algebra

Systems of equations

Here is everything you need to know about systems of equations. You will learn what systems of equations are and how to solve them graphically as well as algebraically.

Students first learn about systems of equations in grade $8$ and expand their knowledge as they progress through high school mathematics.

What are systems of equations?

Systems of equations are two or more algebraic equations that are solved together. They share variables such as $x$ and $y,$ also called unknowns.

For example, the two linear equations below make up a system of equations.

x+y=6

-3x+y=2

The solution to this system would be the point that is common to both equations. If you graph both of the equations, look for their point of intersection.

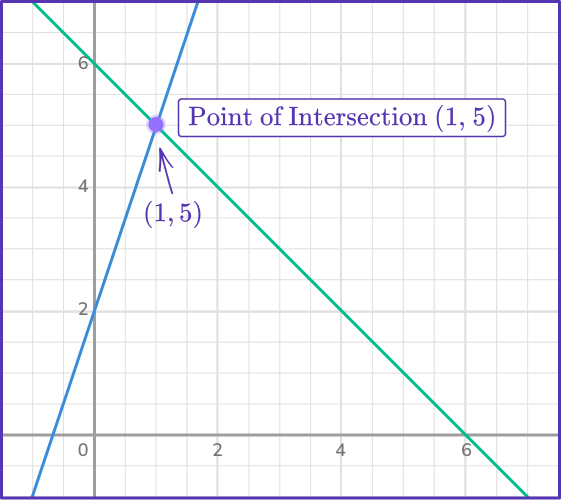
The point of intersection is $(1,5)$ which means that $x=1$ and $y=5$ is the solution to the system. You can substitute $1$ in for $x$ and $5$ in for $y$ into the equations to see that they are the solution.

x+y=6\rightarrow1+5=6\ \checkmark

-3x+y=2\rightarrow-3(1)+5=2\ \checkmark

When solving a system of linear equations there are three possible outcomes.

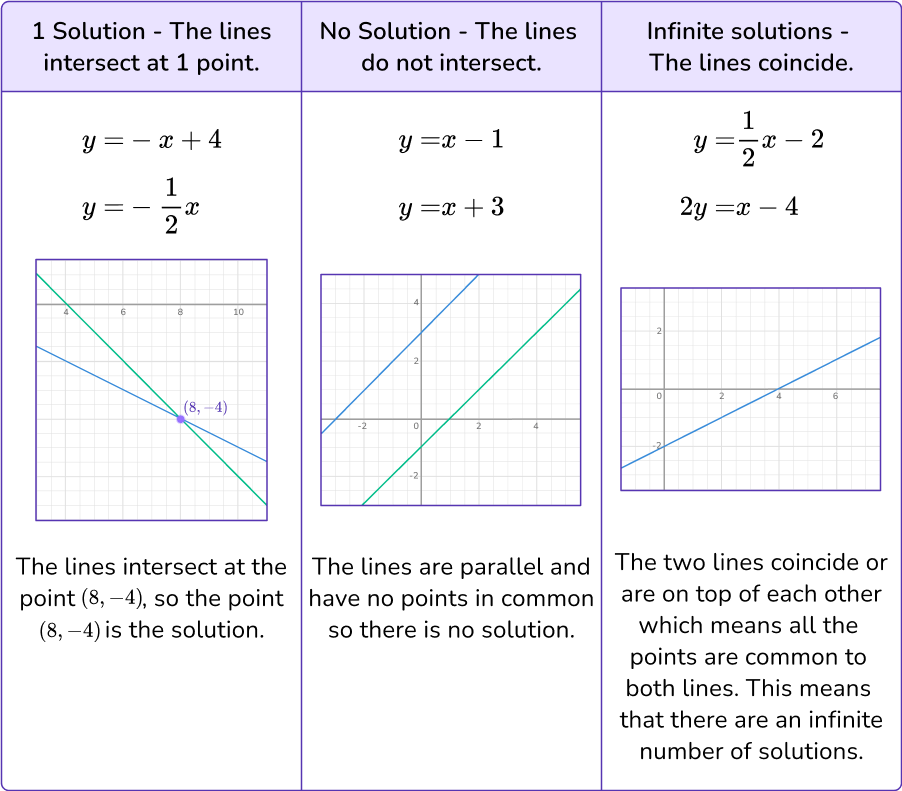
Step-by-step guide: Solving systems of equations by graphing

Step-by-step guide: Intersecting lines

There are two other ways to solve a system of linear equations algebraically.

Substitution method
Elimination method

Substitution method

Let’s solve the system using the substitution method. In order to use substitution, make sure one of the variables is isolated. Then substitute that variable into the other equation and solve.

y=3x+4

y=-2x-6

You can see that the $y’$ s are isolated, so you can substitute $3x+4$ into the second equation for $y.$

\begin{aligned}y&=3x+4 \\\\ y&=-2x-6\end{aligned}

3x+4=-2x-6

This has isolated the $x$ variable so you can now solve for $x.$

\begin{aligned}&3x+4=-2x-6 \\\\ & 3x+2x+4=-2x+2x-6 \\\\ & 5x+4=-6 \\\\ & 5x+4-4=-6-4 \\\\ & 5x=-10\\\\ & \cfrac{5x}{5}=\cfrac{-10}{5}\\\\ & x=-2 \end{aligned}

Now take that value of $x$ and substitute it back into the original equation to find $y.$

\begin{aligned}y&=3(-2)+4\\\\ y&=-6+4 \\\\ y&=-2 \end{aligned}

The solution to the system is $(-2,-2).$

Elimination method

Let’s solve the system using the elimination method (sometimes called the addition method). In order to use this method, you will need to cancel out either the $x$ terms or the $y$ terms.

\begin{aligned}6x+y&=18 \\\\ 4x+y&=14 \end{aligned}

If you were to add the two equations together, neither of the terms would cancel out. The $y$ -terms both have a coefficient of $1.$ If we were to change one of them to have a coefficient of $-1,$ the $y$ -term will cancel out.

So, multiply the top equation by $-1.$

-1(6x+y=18)=-6x-y=-18

Take the new equation and add it to the second equation.

\begin{array}{rcl}-6x&-y&=-18 \\\\ 4x&+y&=14 \\\\ \hline-2x&&=-4 \end{array}

Now, you can solve for $x.$

\begin{aligned}-2x&=-4 \\\\ \cfrac{-2x}{-2}&=\cfrac{-4}{-2}\\\\ x&=2 \end{aligned}

To find $y,$ substitute $2$ for $x$ in one of the original equations.

\begin{aligned}&6x+y=18 \\\\ & 6(2)+y=18 \\\\ & 12+y=18 \\\\ & 12-12+y=18-12 \\\\ & y=6 \end{aligned}

The solution to the system is $(2, 6).$

Solving a system of nonlinear equations

Systems of equations do not always have to be linear. For example, let’s solve the nonlinear system below.

\begin{aligned}y&=x^{2}-4 \\\\ y&=2x-1 \end{aligned}

Using the strategy of substitution, replace $y$ with $2x-1.$

2x-1=x^2-4

It’s a quadratic, so bring everything to one side first so that the quadratic is equal to $0.$ As $x^2$ is positive on the right hand side of the equals sign, move each term onto this side.

\begin{aligned}& 2x-1+1=x^{2}-4+1 \\\\ & 2x=x^{2}-3 \\\\ & 2x-2x=x^{2}-3-2x \\\\ & 0=x^{2}-3-2x \end{aligned}

x^{2}-2x-3=0

Solve by factoring.

\begin{aligned}& x^{2}-2x-3=0 \\\\ & (x-3)(x+1)=0 \\\\ & x=3\text{ or }x=-1 \end{aligned}

Notice how there are two values for $x.$ This means there might be two values for $y.$

Substitute $x=3$ into one of the original equations and then the same for $x=-1.$

\begin{aligned}y&=x^{2}-4 \\\\ y&=(3)^{2}-4 \\\\ y&=9-4 \\\\ y&=5 \end{aligned}

The first ordered pair is $(3,5).$

\begin{aligned}y&=x^{2}-4 \\\\ y&=(-1)^{2}-4 \\\\ y&=1-4 \\\\ y&=-3 \end{aligned}

The second ordered pair is $(-1,-3).$

Graphing the system on the coordinate plane demonstrates how there are two points of intersection which means two solutions.

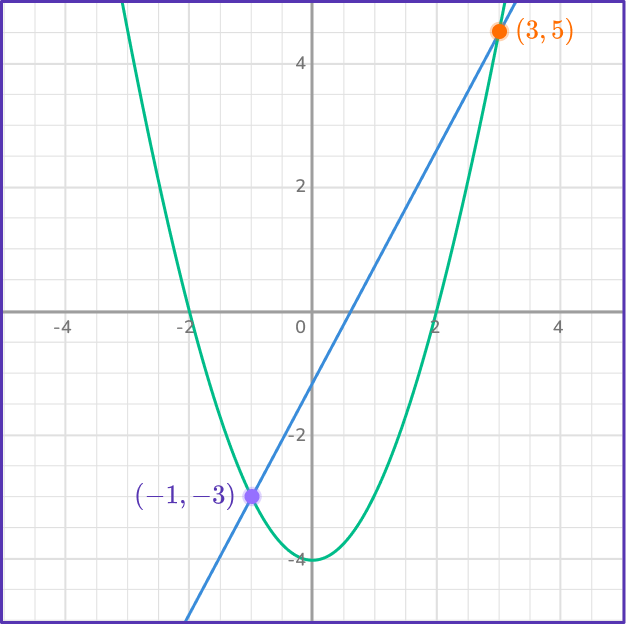
Step-by-step guide: nonlinear systems of equations

What are Systems of equations?

Common Core State Standards

How does this relate to $8$ th grade math and high school math?

Grade 8 Math – Expressions and equations (8.EE.C.8a)
Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.

Grade 8 Math – Expressions and equations (8.EE.C.8b)
Solve systems of two linear equations in two variables algebraically, and estimate solutions by graphing the equations.

High School Algebra – Creating Equations (HSA-CED.A.2)
Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales.

[FREE] Algebra Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 – grade 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th to 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

DOWNLOAD FREE

How to solve systems of equations

In order to solve a system of linear equations using substitution:

Solve one of the equations for either variable.
Substitute the expression from Step $\bf{1}$ into the other equation.
Solve the resulting equation.
Find the other variable.
Write the solution as an ordered pair.

Systems of equations examples

Example 1: substitution

Solve the system using substitution.

\begin{aligned}6x+3y&=48 \\\\ 6x+y&=26 \end{aligned}

Solve one of the equations for either variable.

Using the second equation, solve it for $y.$

\begin{aligned}6x+y&=26 \\\\ 6x-6x+y&=26-6x \\\\ y&=26-6x \end{aligned}

2Substitute the expression from Step $\bf{1}$ into the other equation.

Using the equation that was solved for $y, (y=26-6x)$ substitute into the other equation.

\begin{aligned} 6x+3y&=48 \\\\ 6x+3(26-6x)&=48 \end{aligned}

3Solve the resulting equation.

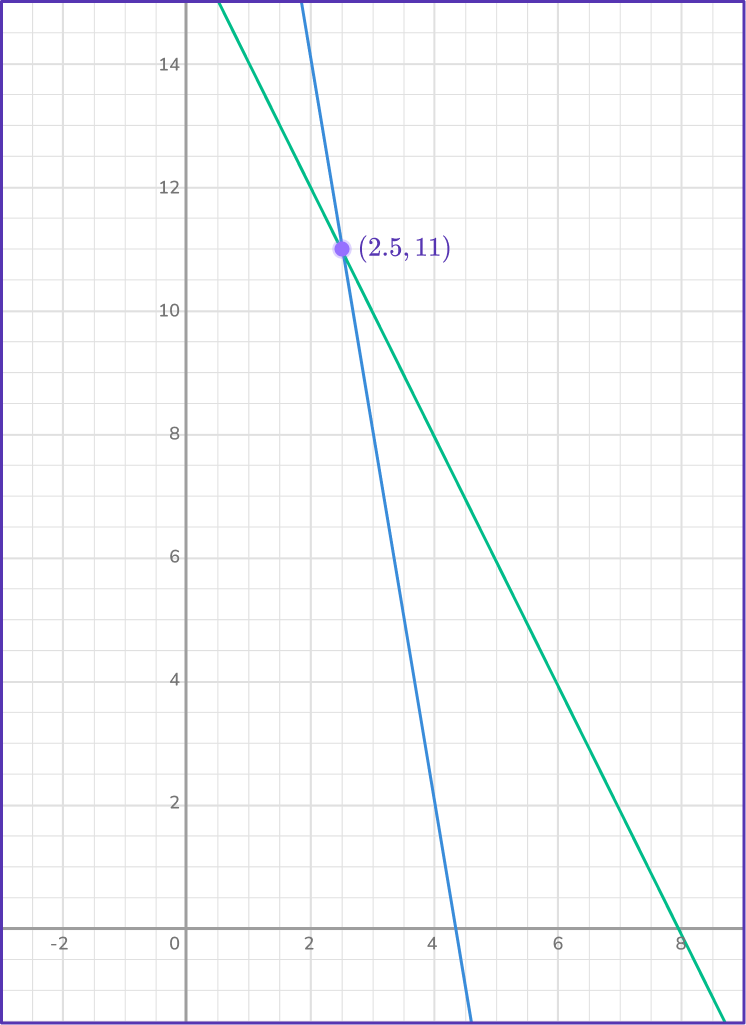
\begin{aligned}6x+3(26-6x)&=48 \\\\ 6x+78-18x&=48 \\\\ -12x+78&=48 \\\\ -12x+78-78&=48-78 \\\\ -12x&=-30 \\\\ \cfrac{-12x}{-12}&=\cfrac{-30}{-12} \\\\ x&=2.5 \end{aligned}

4Find the other variable.

Take $x=2.5$ and substitute it into one of the original equations to find $y.$

\begin{aligned} 6x+3y&=48\\\\ 6(2.5)+3y&=48\\\\ 15+3y&=48\\\\ 15+3y-15&=48-15\\\\ 3y&=33\\\\ y&=11 \end{aligned}

5Write the solution as an ordered pair.

$x=2.5$ and $y=11.$

So, the ordered pair is $(2.5, 11)$ which is the solution of the system.

Example 2: substitution

Solve the system using substitution.

\begin{aligned} y&=\cfrac{1}{2}x \\\\ x-6y&=-8 \end{aligned}

Solve one of the equations for either variable.

The top equation is already solved for $y.$

$y=\cfrac{1}{2}x$

Substitute the expression from Step $\bf{1}$ into the other equation.

Take that equation and substitute it into the second equation.

$\begin{aligned}x-6y&=-8 \\\\ x-6\left(\cfrac{1}{2}x\right)&=-8 \end{aligned}$

Solve the resulting equation.

\begin{aligned}x-6\left(\cfrac{1}{2}x\right)&=-8 \\\\ x-3x&=-8 \\\\ -2x& =-8 \\\\ \cfrac{-2x}{-2}&=\cfrac{-8}{-2} \\\\ x&=4 \end{aligned}

Find the other variable.

Substitute $x=4$ into one of the original equations to find $y.$

$\begin{aligned}& y=\cfrac{1}{2}x \\\\ & y=\cfrac{1}{2}(4) \\\\ & y=2 \end{aligned}$

Write the solution as an ordered pair.

$x=4$ and $y=2$ , so the ordered pair is $(4, 2),$ which is the solution of the system.

Example 3: substitution

Solve the system using substitution.

\begin{aligned}&2x+4y=14 \\\\ & 4x-4y=4 \end{aligned}

Solve one of the equations for either variable.

Using the second equation, solve for $x.$

$\begin{aligned}4x-4y&=4 \\\\ 4x-4y+4y&=4+4y \\\\ 4x&=4+4y \\\\ \cfrac{4x}{4}&=\cfrac{4}{4}+\cfrac{4y}{4} \\\\ x &=1+y \end{aligned}$

Substitute the expression from Step $\bf{1}$ into the other equation.

Substitute into the first equation.

$\begin{aligned}2x+4y&=14 \\\\ 2(1+y)+4y&=14 \end{aligned}$

Solve the resulting equation.

\begin{aligned}2(1+y)+4y&=14 \\\\ 2+2y+4y&=14 \\\\ 6y&=12 \\\\ y&=2 \end{aligned}

Find the other variable.

Substitute $y=2$ into one of the original equations to find $x.$

$\begin{aligned}2x+4y&=14 \\\\ 2x+4(2)&=14 \\\\ 2x+8&=14 \\\\ 2x+8-8&=14-8 \\\\ 2x&=6 \\\\ \cfrac{2x}{2}&=\cfrac{6}{2} \\\\ x&=3 \end{aligned}$

Write the solution as an ordered pair.

$y=2$ and $x=3,$ so the ordered pair is $(3, 2),$ which is the solution of the system.

How to solve systems of equations

In order to solve a system of equations using elimination:

Make the coefficients of the variable opposites.
Add the equations to eliminate that variable.
Solve for the remaining variable.
Substitute the solved variable into the original equation to find the eliminated variable.
Write the answer as an ordered pair.

Example 4: elimination

Solve the system using elimination.

\begin{aligned} 6a+b&=18 \\\\ 4a+b&=14\end{aligned}

Make the coefficients of the variable opposites.

To eliminate the $“b”$ variable, the coefficients have to be opposites. In this case, the coefficients should be $1$ and $-1.$

Multiplying the top equation by $-1,$ makes the coefficient $-1.$

$\begin{aligned} -1(6a+b&=18) \\\\ -6a-b&=-18 \end{aligned}$

Add the equations to eliminate that variable.

Using the new equation and the second equation, add the equations together.

\begin{array}{rcl}-6a&-b&=-18 \\\\ 4a&+b&=14 \\\\ \hline -2a&&=-4 \end{array}

Solve for the remaining variable.

\begin{aligned}-2a&=-4 \\\\ \cfrac{-2a}{-2}&=\cfrac{-4}{-2} \\\\ a&=2 \end{aligned}

Substitute the solved variable into the original equation to find the eliminated variable.

Substituting $a=2$ into one of the original equations, solve for $b.$

$\begin{aligned}6a+b&=18 \\\\ 6(2)+b&=18 \\\\ 12+b&=18 \\\\ b&=6 \end{aligned}$

Write the answer as an ordered pair.

$a=2$ and $b=6$ , so the ordered pair is $(2,6)$ , which is the solution of the system.

Example 5: elimination

Solve the system using elimination.

\begin{aligned}3x+2y&=8 \\\\ 2x+5y&=-2 \end{aligned}

Make the coefficients of the variable opposites.

In this case, let’s make the coefficients of the $x$ terms opposites. Make one $6$ and the other $-6.$

Multiply the top equation by $2$ and the bottom equation by $-3.$

$\begin{aligned}2(3x+2y=8)&\rightarrow6x+4y=16 \\\\ -3(2x+5y=-2)&\rightarrow-6x-15y=6 \end{aligned}$

Add the equations to eliminate that variable.

\begin{array}{rcl}6x&+4y&=16 \\\\ -6x&-15y&=6 \\\\ \hline &-11y&=22 \end{array}

Solve for the remaining variable.

\begin{aligned} -11y&=22 \\\\ \cfrac{-11y}{-11}&=\cfrac{22}{-11} \\\\ y&=-2 \end{aligned}

Substitute the solved variable into the original equation to find the eliminated variable.

Substitute $y=-2$ into one of the original equations to find $y.$

$\begin{aligned}3x+2y&=8 \\\\ 3x+2(-2)&=8 \\\\ 3x-4&=8 \\\\ 3x-4+4&=8+4 \\\\ 3x&=12 \\\\ \cfrac{3x}{3}&=\cfrac{12}{3} \\\\ x&=4 \end{aligned}$

Write the answer as an ordered pair.

$y=-2$ and $x=4$ , so the ordered pair is $(4,-2)$ , which is the solution of the system.

Example 6: elimination

Solve the system using elimination.

\begin{aligned}10x-9y&=46 \\\\ 2x-3y&=-10 \end{aligned}

Make the coefficients of the variable opposites.

In this case, let’s eliminate the $x$ variables. This means the coefficients have to be $10$ and $-10.$ The top equation already has a coefficient of $10.$ The bottom equation has to be multiplied by $-5.$

$-5(2x-3y=-10)\rightarrow-10x+15y=50$

Add the equations to eliminate that variable.

\begin{array}{rcl}10x&-9y&=46 \\\\ -10x&+15y&=50 \\\\ \hline &6y&=96 \end{array}

Solve for the remaining variable.

\begin{aligned}6y&=96 \\\\ \cfrac{6y}{6}&=\cfrac{96}{6} \\\\ y&=16 \end{aligned}

Substitute the solved variable into the original equation to find the eliminated variable.

Substitute $y=16$ into one of the original equations in order to find the value of $x.$

$\begin{aligned}10x-9y&=46 \\\\ 10x-9(16)&=46 \\\\ 10x-144&=46 \\\\ 10x-144+144&=46+144 \\\\ 10x&=190 \\\\ \cfrac{10x}{10}&=\cfrac{190}{10} \\\\ x&=19 \end{aligned}$

Write the answer as an ordered pair.

$y=16$ and $x=19$ , so the ordered pair is $(19,16)$ , which is the solution of the system.

Example 7: word problem

David buys $10$ apples and $6$ bananas at the farm. They cost $\$ 5.08$ in total.

At the same farm, Ellie buys $3$ apples and $1$ banana. She spends $\$ 1.42$ in total.

Find the cost of one apple and one banana.

Use the substitution method to solve.

Additional step: Create two equations from the given word problem.

Convert the word problem into equations.

$10$ apples and $6$ bananas for $\$ 5.08 \rightarrow10a+6b=5.08$

$3$ apples and $1$ banana for $\$ 1.42 \rightarrow3a+b=1.42$

Using substitution:

Solve one of the equations for either variable.

\begin{aligned}10a+6b&=5.08 \\\\ 3a+b&=1.42\end{aligned}

Using the second equation, solve it for $b.$

\begin{aligned}3a+b&=1.42 \\\\ 3a-3a+b&=1.42-3a \\\\ b&=1.42-3a \end{aligned}

Substitute the expression from Step $\bf{2}$ into the other equation.

\begin{aligned}&10a+6b=5.08 \\\\ &b=1.42-3a \end{aligned}

$10a+6(1.42-3a)=5.08$

Solve the resulting equation.

\begin{aligned}10a+6(1.42-3a)&=5.08 \\\\ 10a+8.52-18a&=5.08 \\\\ -8a+8.52&=5.08 \\\\ -8a+8.52-8.52&=5.08-8.52 \\\\ -8a&=-3.44 \\\\ \cfrac{-8a}{-8}&=\cfrac{-3.44}{-8} \\\\ a&=0.43 \end{aligned}

Find the other variable.

Substitute $a=0.43$ into one of the original equations to find the value of $b.$

$\begin{aligned}10a+6b&=5.08 \\\\ 10(0.43)+6b&=5.08 \\\\ 4.3+6b&=5.08 \\\\ 4.3+6b-4.3&=5.08-4.3 \\\\ 6b&=0.78 \\\\ \cfrac{6b}{6}&=\cfrac{0.78}{6} \\\\ b&=0.13 \end{aligned}$

Write the solution as an ordered pair.

$a=0.43$ , which means each apple costs $\$ 0.43$

$b=0.13$ , which means each banana costs $\$ 0.13.$

Teaching tips for systems of equations

Have students use digital platforms like Desmos to explore the different types of solutions for systems of equations.

Instead of practice worksheets, have students work in collaborative groups and practice problems on whiteboards.

Easy mistakes to make

Eliminating a variable incorrectly
Using addition to eliminate one variable when the coefficients are not opposites of each other.
For example,

$\begin{aligned}x+2y&=9 \\\\ x+y&=3 \end{aligned}$

Adding the equations together and eliminating $x$ when they are not eliminated.

$\begin{array}{rcl}x&+2y&=9 \\\\ x&+y&=3 \\\\ \hline 2x&+3y&=12 \end{array}$

Multiplying one of the equations by $-1$ makes the coefficients of the $x’$ s opposite.

$-1(x+2y=9)\rightarrow-x-2y=-9$

Not multiplying every term in the equation
For example,

$\begin{aligned}x+3y&=8 \\\\ x+y&=-9 \end{aligned}$

To use elimination, multiply the entire first equation by $-1.$

$-1(x+3y=8)$ ≠ $-x-3y=8$

$-1(x+3y=8)=-x-3y=-8 \; { \color{lightgreen} ✔ }$

Only finding the value of one variable and not the other
When solving a system, find the value of each variable. The solution is the point of intersection, so there needs to be two solutions so that you can express the answer as an ordered pair.

Practice system of equations questions

x=\cfrac{5}{2}=2.5, \; y=11

x=11, \; y=\cfrac{5}{2}=2.5

x=6, \; y=1

x=3, \; y=6

Using the substitution method, solve the second equation for $y.$

\begin{aligned}6x+y&=26 \\\\ 6x-6x+y&=26-6x \\\\ y&=26-6x \end{aligned}

Then take that and substitute it into the first equation for $y.$

\begin{aligned}6x+3y&=48 \\\\ 6x+3(26-6x)&=48 \\\\ 6x+78-18x&=48 \\\\ -12x+78&=48 \\\\ -12x+78-78&=48-78 \\\\ -12x&=-30 \\\\ \cfrac{-12x}{-12}&=\cfrac{-30}{-12} \\\\ x&=2.5 \end{aligned}

Substitute the value of $x=2.5$ into one of the original equations to find the value of $y.$

\begin{aligned}6x+3y&=48 \\\\ 6(2.5)+3y&=48 \\\\ 15+3y&=48 \\\\ 15-15+3y&=48-15 \\\\ 3y&=33 \\\\ \cfrac{3y}{3}&=\cfrac{33}{3} \\\\ y&=11 \end{aligned}

Since $x=2.5$ and $y=11,$ the ordered pair is $(2.5,11).$

Systems of Equations 4 US

Systems of Equations 4 US-1

Systems of Equations 5 US

Systems of Equations 6 US

No solution to a system means that there are no common points between the equations.

Parallel lines represent no solution because there are not any common points.

x=1, \; y=2

x=1, \; y=3

x=18, \; y=5

x=8, \; y=3

You can use elimination to solve the system by eliminating the $x$ variables by making the coefficients opposites. Multiply the top equation by $-1.$

-1(x-2y=8)=-x+2y=-8

Add the equations together to eliminate the $x.$

\begin{array}{rcl}-x&+2y&=-8 \\\\ x&-3y&=3 \\\\ \hline &-y&=-5 \end{array}

Solve for $y.$

\begin{aligned}-y&=-5 \\\\ \cfrac{-y}{-1}&=\cfrac{-5}{-1} \\\\ y&=5\\\end{aligned}

Take $y=5$ and substitute it into one of the original equations to find $x.$

\begin{aligned}x-2y&=8 \\\\ x-2(5)&=8 \\\\ x-10&=8 \\\\ x&=18 \end{aligned}

$x=18$ and $y=5,$ so the ordered pair is $(18,5)$

(4, \, 2)

(4, \, 9)

(3, \, 1)

(3, \,2)

Using the elimination strategy, multiply the bottom equation by $-2$ to eliminate the $y$ variables by making the coefficients opposites of each other.

-2(3x+y=21)=-6x-2y=-42

Add the equations together to eliminate the $y$ variables.

\begin{array}{rcl}-6x&-2y&=-42 \\\\ 4x&+2y&=34 \\\\ \hline -2x&&=-8 \end{array}

Solve for $x.$

\begin{aligned}-2x&=-8 \\\\ \cfrac{-2x}{-2}&=\cfrac{-8}{-2} \\\\ x&=4 \end{aligned}

Substitute $4$ in for $x$ into one of the original equations to find the value of $y.$

\begin{aligned}4x+2y&=34 \\\\ 4(4)+2y&=34 \\\\ 16+2y&=34 \\\\ 2y&=18 \\\\ \cfrac{2y}{2}&=\cfrac{18}{2} \\\\ y&=9 \end{aligned}

$x=4$ and $y=9$ , so the ordered pair is $(4,9).$

(6, \, 2)

(15, \, 4)

(5, \, 9)

(-6, \, -2)

Solving the system using the elimination method, multiply the bottom equation by $-3$ to eliminate the $x$ variables.

-3(5x-9y=12)=-15x+27y=-36

Add the equations together to eliminate the $x$ variables.

\begin{array}{rcl}15x&-4y&=82 \\\\ -15x&+27y&=-36 \\\\ \hline &23y&=46 \end{array}

Solve for $y.$

\begin{aligned}23y&=46 \\\\ \cfrac{23y}{23}&=\cfrac{46}{23} \\\\ y&=2 \end{aligned}

Substitute $2$ in for $y$ to find the value of $x.$

\begin{aligned}15x-4y&=82 \\\\ 15x-4(2)&=82 \\\\ 15x-8&=82 \\\\ 15x&=90 \\\\ x&=6 \end{aligned}

$x=6$ and $y=2$ , so the ordered pair is $(6,2).$

$5$ dimes and $7$ nickels

$6$ dimes and $6$ nickels

$8$ dimes and $4$ nickels

$5$ nickels and $7$ dimes

Translate the problem into algebraic equations.

$12$ coins total $\rightarrow{n}+d=12$

The coins total $\$ 0.95 \rightarrow 0.05n+0.1d=0.95$

Using substitution strategy, solve the first equation for $n.$

\begin{aligned}n+d&=12 \\\\ n&=12-d \end{aligned}

Substitute $n$ into the second equation.

\begin{aligned}0.05n+0.1d&=0.95 \\\\ 0.05(12-d)+0.1d&=0.95 \\\\ 0.6-0.05d+0.1d&=0.95 \\\\ 0.05d&=0.35 \\\\ d&=7 \end{aligned}

Substitute $7$ in for d into one of the original equations to find $n.$

\begin{aligned}n+d&=12 \\\\ n+7&=12 \\\\ n&=5 \end{aligned}

$7$ dimes and $5$ nickels.

System of equations FAQs

Are there other ways to solve systems of linear equations?

Yes, as noted on this webpage, you can use elimination method and substitution method, which are common strategies to solve linear systems in Algebra $1.$

However, you can also use matrices (rectangular arrangements of numbers) to solve linear equations. When you get into high school Algebra $2$ and Precalculus, you will learn how to solve linear systems using matrices and Cramer’s rule.

Can linear systems of equations have fractions as solutions?

Yes, the solutions to linear systems or any system can be any real number.

What are simultaneous equations?

Simultaneous equations is just different terminology for systems of equations.

Can you solve a system of linear inequalities?

Yes, graphing is the preferred method for solving a system of linear inequalities.

The next lessons are

Factorizing
Surds
Vectors

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.