Intersecting Lines - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Types of graphs

Straight line graphs

Rate of change

Math resources Algebra Systems of equations

Intersecting lines

Here you will learn about intersecting lines, including how to find the point of intersection of two straight lines and how to solve simultaneous equations graphically and algebraically.

Students will first learn about intersecting lines and other line segments in $4$ th and $5$ th grade as a part of geometry, and again in $8$ th grade and high school as a part of expressions and equations.

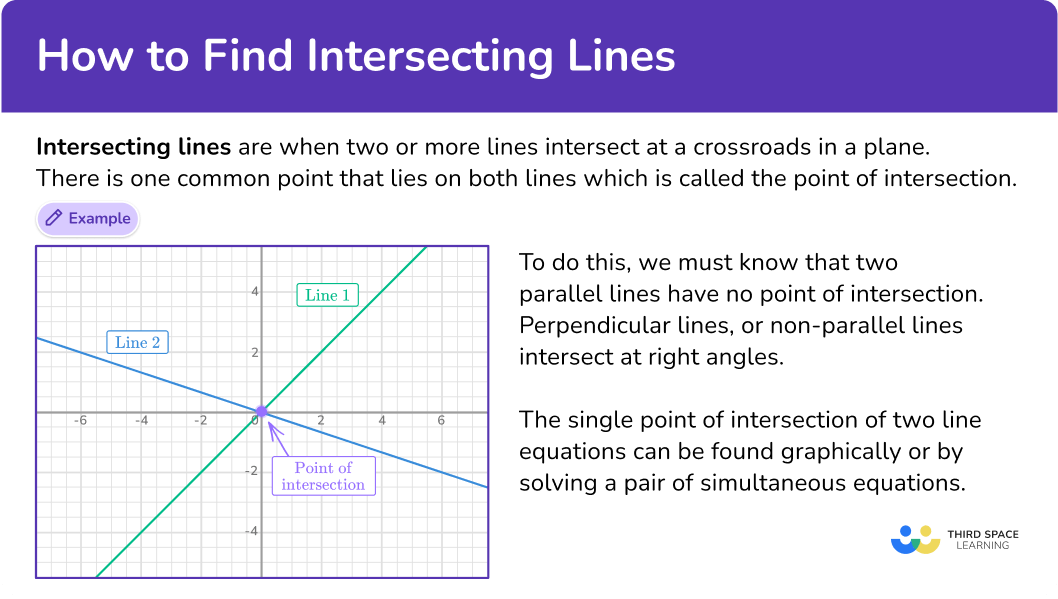
What are intersecting lines?

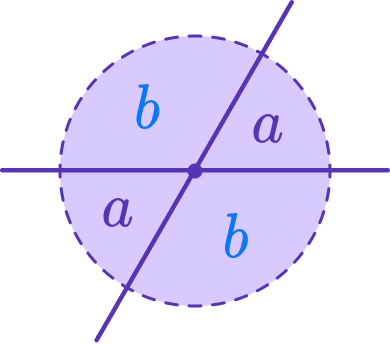
Intersecting lines are when two or more lines cross each other in a plane at a crossroads. There is one common point that lies on both lines, which is called the point of intersection.

Two straight intersecting lines meet and create pairs of vertically opposite angles (or vertical angles). One of the important properties of intersecting lines is that each pair of vertically opposite angles is equal.

Let’s look at examples of lines on the Cartesian coordinate plane.

In this example, the two given lines, Line $1$ and Line $2$ , have one intersection point.

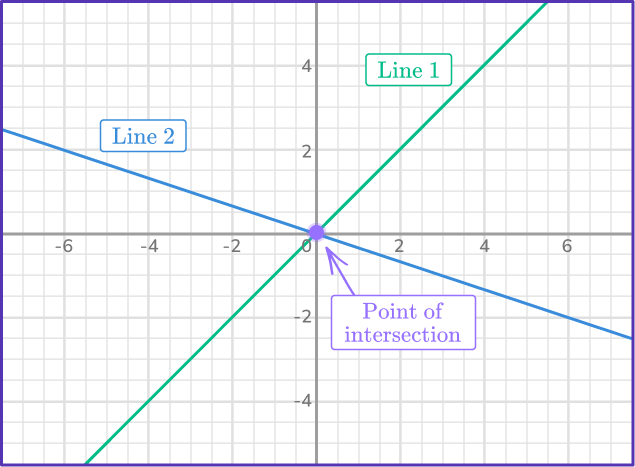
The equation of Line $1$ is $y=x$ and the equation of Line 2 is $y=-\cfrac{1}{3}$ . The point of intersection (common point) is the ordered pair $(0, 0).$

In this next example, the two lines on the coordinate plane do not have any common point of intersection. They are considered to be parallel lines which means they are non-intersecting lines.

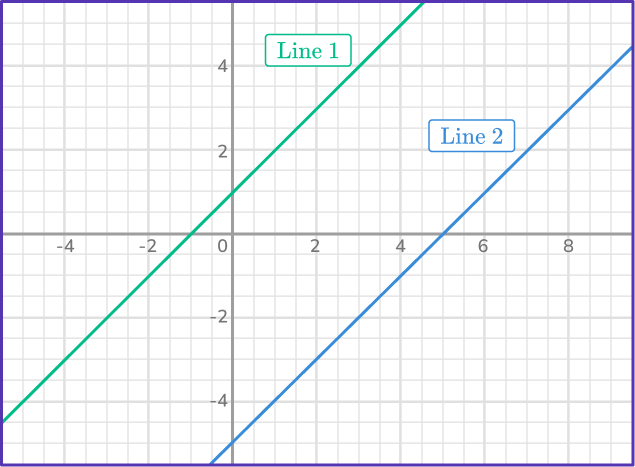
The equation of Line $1$ is $y=x+1$ and the equation of Line $2$ is $y=x-5.$

The slope of Line $1$ is $1$ and the slope of Line $2$ is $1.$ Notice how the slopes are the same. Parallel lines will always have the same slope because they will not intersect.

Let’s look at another example. Notice how the lines intersect on the coordinate plane. However, they have a special relationship with one another. They are considered to be perpendicular lines because they form a right angle at their point of intersection.

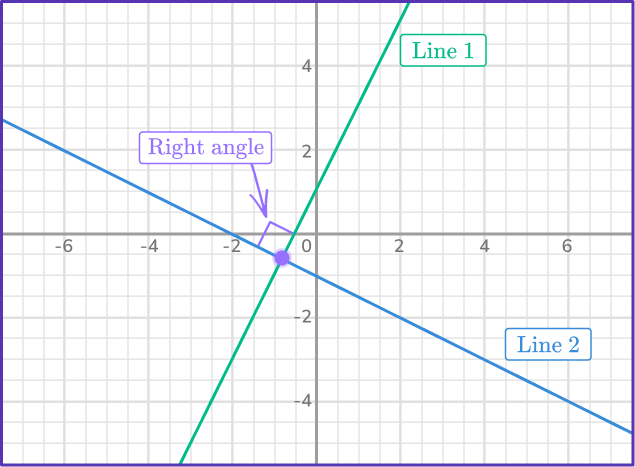
The equation of Line $1$ is $y=2x+1$ and the equation of Line $2$ is $y=-\cfrac{1}{2}-1$ .

The slope of Line $1$ is $2$ and the slope of Line $2$ is $-\cfrac{1}{2}$ . Notice how the slopes are opposite reciprocals of each other. Their product is also $-1.$

2 \times -\cfrac{1}{2} = -\cfrac{2}{2} = -1

Perpendicular lines will always have opposite reciprocal slopes which means the product of their slopes will always be $-1.$

This idea links the two concepts of coordinate geometry and algebra. If you are given the equations of two intersecting lines, or a graph of the two equations, the point of intersection of two line segments is the solution to that pair of linear simultaneous equations.

In three dimensions, it is possible to have two line segments which are not parallel but also not in the same plane – these are called skew lines, and will not have a common point of intersection or crossroads.

What are intersecting lines?

Common Core State Standards

How does this relate to $4$ th grade math and $5$ th grade math?

Grade 4 – Geometry (4.G.A.1)
Draw points, lines, line segments, rays, angles (right, acute, obtuse), and perpendicular and parallel lines. Identify these in two-dimensional figures.

Grade 5 – Geometry (5.G.A.1)
Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the $0$ on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates.

Understand that the first number indicates how far to travel from the origin in the direction of one axis, and the second number indicates how far to travel in the direction of the second axis, with the convention that the names of the two axes and the coordinates correspond (e.g., $x-$ axis and $x-$ coordinate, $y-$ axis and $y-$ coordinate).

Grade 8 – Expressions and Equations (8.EE.C.8a)
Understand that solutions to a system of two linear equations in two variables correspond to points of intersection of their graphs, because points of intersection satisfy both equations simultaneously.

High School Algebra – Reasoning with Equations and Inequalities (HSA.REI.C.6)
Solve systems of linear equations exactly and approximately (e.g., with graphs), focusing on pairs of linear equations in two variables.

[FREE] Intersecting Lines Worksheet (Grade 8 and High School)

Use this worksheet to check your 8th grade and high school students’ understanding of intersecting lines. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Intersecting Lines Worksheet (Grade 8 and High School)

Use this worksheet to check your 8th grade and high school students’ understanding of intersecting lines. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to use intersecting lines

In order to find the point of intersection using a graph:

Plot the graph of the first equation.
On the same set of axes, plot the graph of the second equation.
Write down the coordinates of the crossroads or point of intersection.

Point of intersection using a graph examples

Example 1: finding the point of intersection using a graph

Find the point of intersection of the lines $y=x+4$ and $y=2x-3.$

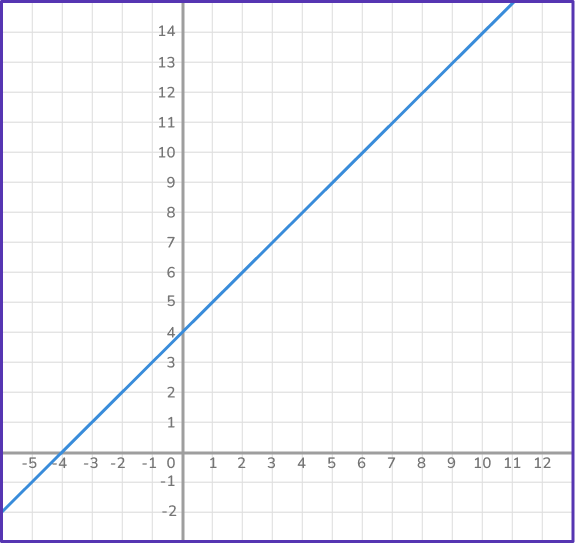
Plot the graph of the first equation.

First plot a graph of the equation $y=x+4.$

Draw a table of values $(3$ or $4$ points are sufficient $).$

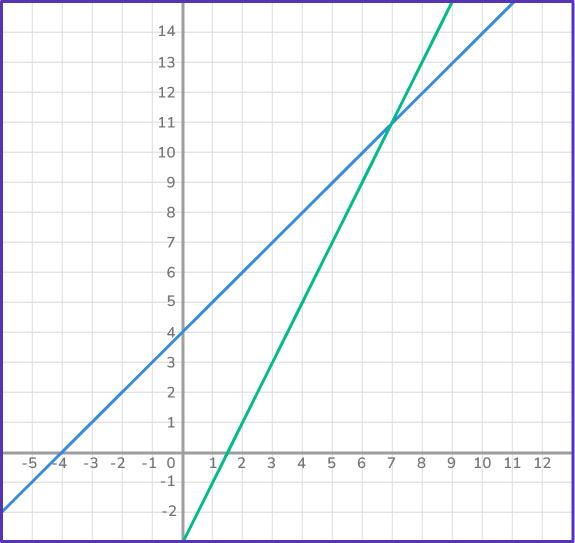
2On the same set of axes, plot the graph of the second equation.

Next, plot the graph of the second equation, $y=2x-3$ , on the same set of axes.

Draw a table of values $(3$ or $4$ points are sufficient $).$

3Write down the coordinates of the point of intersection.

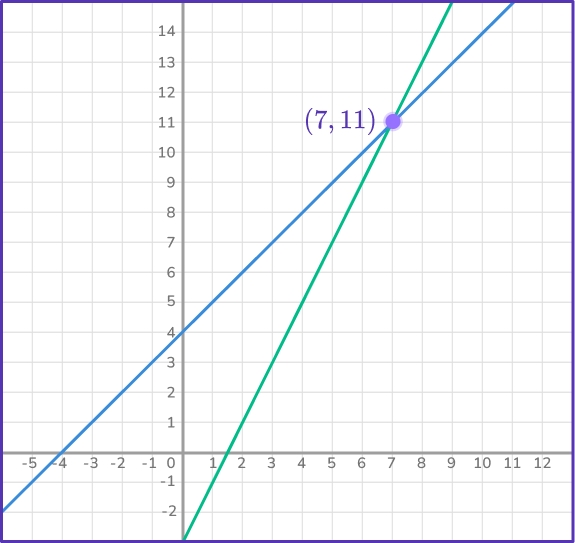
Simply read the coordinates from the graph – the point of intersection is $(7,11).$

Example 2: finding the point of intersection on a graph

Find the point of intersection of the lines $3x+4y=20$ and $2x-2y=4.$

Plot the graph of the first equation.

First plot a graph of the equation $3x+4y=20.$

Draw a table of values $(3$ or $4$ points are sufficient $).$

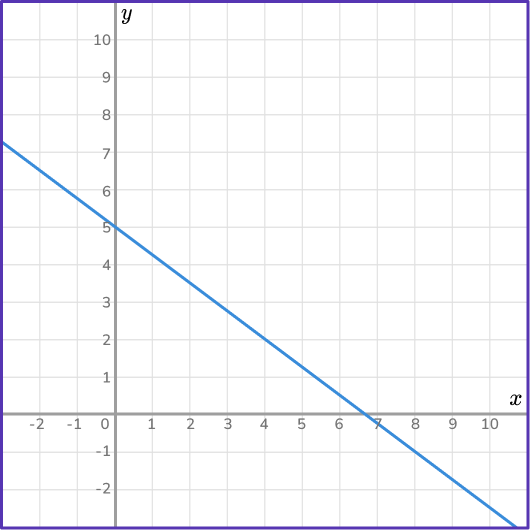
On the same set of axes, plot the graph of the second equation.

Next, plot the graph of the second equation, $2x-2y=4$ , on the same set of axes.

Draw a table of values $(3$ or $4$ points are sufficient).

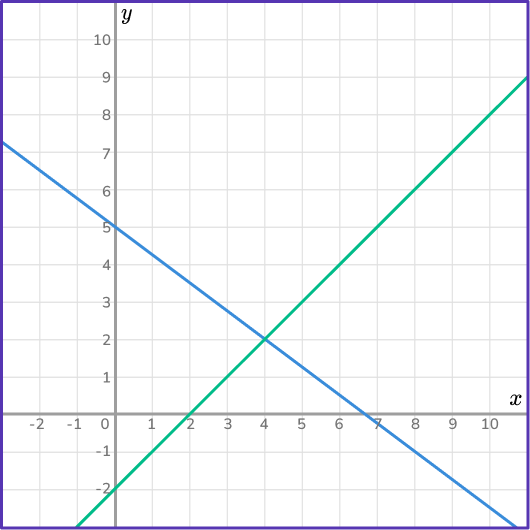
Write down the coordinates of the point of intersection.

Read the coordinates from the graph – the point of intersection is $(4,2).$

Finding the point of intersection algebraically

Sometimes the point of intersection is not easy to read from a graph (for example, if it is a fraction or decimal), and drawing a graph is quite a long process.

If you are working with two linear equations, you can solve them algebraically as a pair of simultaneous equations to find the point of intersection.

How to find the point of intersection algebraically

In order to find the point of intersection algebraically, you follow the steps for solving simultaneous linear equations:

Eliminate one variable.
Find the value of the other variable.
Find the value of the remaining variable via substitution.

Point of intersection using simultaneous equations examples

Example 3: finding the point of intersection algebraically

Find the point of intersection of the lines $3x+4y=20$ and $2x-2y=4.$

Note that this is the same pair of equations you considered in example $2$ above – here you will look at the algebraic method, which results in the same answer.

Eliminate one variable.

$(1) \; 3x+4y=20$

$(2) \; 2x-2y=4$

Multiply equation $(2)$ by $2$ to get,

$(1) \; 3x+4y=20$

$(2) \; 4x-4y=8$

Then add the two equations together to eliminate $y.$

$7x=28$

Find the value of the other variable.

$7x=28$

$x=4$

Find the value of the remaining variable via substitution.

You now know that $x=4,$ so you can find the value of $y$ by substituting this value of $x$ into either of the two original equations.

\begin{array}{r} 3 x+4 y=20 \\\\ 3(4)+4 y=20 \\\\ 12+4 y=20 \\\\ 4 y=8 \\\\ y=2 \end{array}

So the point of intersection is $(4, 2).$

Example 4: finding the point of intersection algebraically

Find the point of intersection of the lines $2x+3y=20$ and $y=x-5.$

Eliminate one variable.

Here you can substitute the expression $y=x-5$ into $2x+3y=20.$

\begin{array}{r} 2 x+3 y=20 \\\\ 2 x+3(x-5)=20 \\\\ 2 x+3 x-15=20 \\\\ 5 x-15=20 \end{array}

Find the value of the other variable.

\begin{aligned} 5 x-15 &=20 \\\\ 5 x &=35 \\\\ x &=7 \end{aligned}

Find the value of the remaining variable via substitution.

You now know that $x=7,$ so you can find the value of $y$ by substituting this value of $x$ into either of the two original equations.

\begin{aligned} 2 x+3 y &=20 \\\\ 2(7)+3 y &=20 \\\\ 14+3 y &=20 \\\\ 3 y &=6 \\\\ y &=2 \end{aligned}

So the point of intersection is $(7, 2).$

Showing that intersecting lines are parallel or perpendicular

Two lines are parallel if they have the same gradient.

Two lines are perpendicular if the product of their gradients is $-1.$

By considering the gradients of the two lines, you can decide whether they are parallel lines, perpendicular lines or neither.

How to show that lines are parallel or perpendicular

In order to decide whether two lines are parallel lines, perpendicular lines or neither:

Rearrange both equations to the form $\bf{\textbf{y}=\textbf{mx}+\textbf{b}}$ .
Compare the slopes to decide if they are parallel lines, perpendicular lines or neither.

Example 5: a pair of parallel lines

Show that the lines $y=3x+5$ and $6x-2y=24$ are parallel and do not have a point of intersection.

Rearrange both equations to the form $\bf{\textbf{y}=\textbf{mx}+\textbf{b}}$ .

The first equation is already in the correct form.

Rearrange the second equation.

\begin{aligned} 6 x-2 y &=24 \\\\ 6 x &=2 y+24 \\\\ 6 x-24 &=2 y \\\\ 3 x-12 &=y \end{aligned}

Compare the slopes to decide if they are parallel lines, perpendicular lines or neither.

The equations of the lines are,

$y=3x+5$

$y=3x-12$

The gradient of each equation is $3,$ hence the lines are parallel. Since they are parallel lines they do not intersect.

Example 6: a pair of perpendicular lines

Show that the lines $6x+2y=30$ and $3y-x=24$ are perpendicular and intersect at right angles.

Rearrange both equations to the form $\bf{\textbf{y}=\textbf{mx}+\textbf{b}}$ .

Rearrange the first equation.

$\begin{array}{r} 6 x+2 y=30 \\\\ 2 y=30-6 x \\\\ y=15-3 x \end{array}$

Rearrange the second equation.

\begin{aligned} 3 y-x &=24 \\\\ 3 y &=24+x \\\\ y &=8+\cfrac{1}{3} x \end{aligned}

Compare the slopes to decide if they are parallel lines, perpendicular lines or neither.

The equations of the lines are,

\begin{aligned} &y=15-3 x \\\\ &y=8+\cfrac{1}{3} x \end{aligned}

Multiplying the gradients together to find their product.

$-3 \times \cfrac{1}{3}=\cfrac{-3}{3}=-1.$

The product of the gradients is $-1,$ so the lines are perpendicular and intersect at $90$ degrees.

Teaching tips for how to find the intersecting lines

Make the words “parallel” and “intersecting” memorable by pointing out that the two $"l"$ letters in the word parallel are, in fact, just that – parallel. The letter $"t"$ in “intersecting” is also an example of lines that cross. This memory device should help children remember which word represents which kind of line relationship.

Help students locate physical and real world examples in door and window frames, floor tiles, ceiling beams, fences, parking lots, and road stripes to identify parallel and perpendicular lines. When identifying perpendicular lines, ask students to locate the point of intersection.

Have students use digital platforms such as Desmos so they can explore the relationship between parallel and perpendicular lines.

Easy mistakes to make

Concluding that two lines do not intersect because the point of intersection is not visible in the drawn range of the graph. For example, the lines $y=2x+4$ and $y=4x-5$ actually intersect at the point $(4.5, 13).$

Not rearranging to the form $y=mx+b$ when comparing gradients. For example, the equations $y=2x+7$ and $2y+2x=4$ are not parallel, even though the coefficient of $x$ is $2$ in each case. Here you would need to rearrange the second equation to $y=2-x.$ You can now see that the gradient is $-1$ and the lines are therefore not parallel.

Practice intersecting lines questions

(2, 3)

(1, 4)

(4, 1)

(3,8)

Draw a table of values for each equation and plot as below.

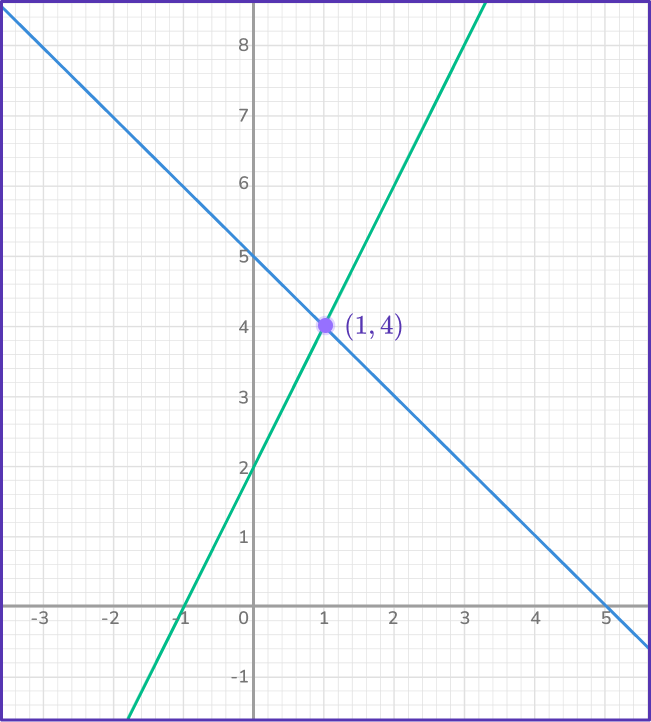
US Webpages_ Intersecting lines 15

Read the point of intersection from the graph $(1,4).$

(2, -4)

(10, 2)

(6, 8)

(5,5)

Draw a table of values for each equation and plot as below.

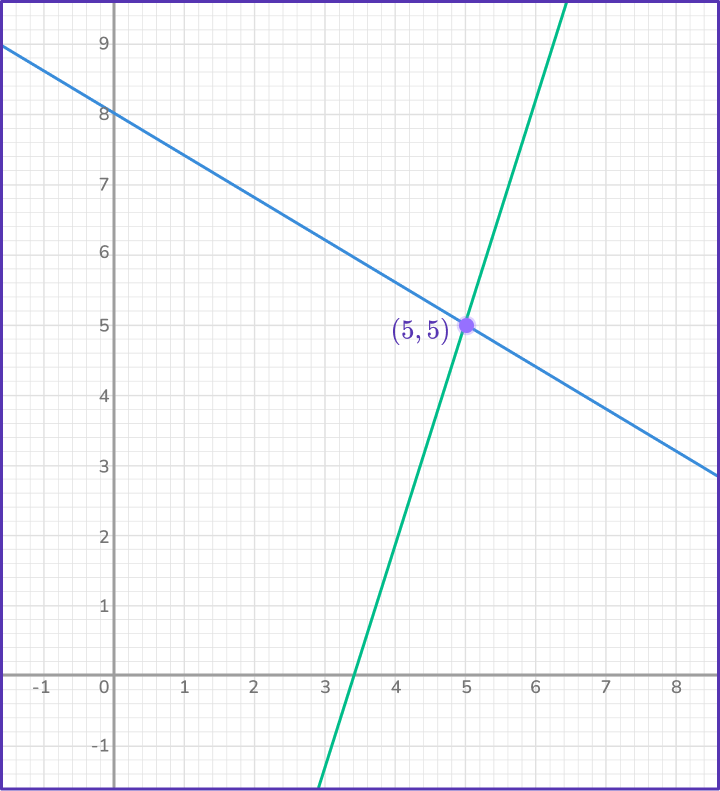
US Webpages_ Intersecting lines 16

Read the point of intersection from the graph $(5,5).$

(8, 2)

(20, 10)

(5, 5)

(2,8)

Add the two equations together to eliminate $y$ and get $5x=40.$

Solve to get $x=8.$

Then substitute $x=8$ into one of the original equations to get $y=2.$

(8, 5)

(3, 4)

(6, 10)

(3,10)

Substitute $y=2x-2$ into $5x+2y=50$ to get $5x+2(2x-2)=50.$

Expand the brackets and solve to get $x=6.$

Finally, substitute into one of the original equations to get $y=10.$

Parallel, no intersection

Perpendicular, the points intersect at $(4, 6)$

Neither, the points intersect at $(4, 6)$

Neither, the points intersect at $(2,0)$

Rearranging $12x-3y=24$ to $12x-24=3y$ and then dividing by $3$ gives the equation $y=4x-8.$

Both lines have the same gradient $(4),$ so they are parallel and do not intersect.

Parallel lines, no intersection

Perpendicular lines, the points intersect at $(2, 6)$

Neither, the points intersect at $(2, 6)$

Neither, the points intersect at $(4,5)$

Multiply the first equation by $2$ to get $2y=10x-8,$ then set this equal to the second equation to get $10x-8=3x+6.$

Solve the equation to get $x=2,$ and substitute into one of the original equations to get $y=6.$

Finally, check the slopes.

Dividing the equation $2y=3x+6$ by $2$ gives $y=\cfrac{3}{2} x+3.$

So the two gradients are $5$ and $\cfrac{3}{2}.$

These do not have a product of $-1,$ so the lines are not perpendicular.

How to find intersecting lines FAQs

What is the point of intersection?

The point of intersection is a unique point where two or more lines cross each other. In a two-dimensional coordinate system, this point has the same $x$ and $y$ coordinates on each of the intersecting lines.

In the context of geometry, the point of intersection holds significance as it represents the common ground shared by the intersecting lines, which can be useful in solving various mathematical problems.

Are perpendicular lines always intersecting lines?

Yes, perpendicular lines are always intersecting lines because they meet at a $90^{\circ}$ angle. By definition, perpendicular lines are two lines that cross each other to form a right angle. Since they cross, they must have a common point, which is known as the point of intersection.

In coordinate geometry, the slopes of two perpendicular lines are negative reciprocals of each other, ensuring that they will intersect at a single point.

How can I determine if two lines are intersecting or parallel?

To determine if two lines are intersecting or parallel, you need to examine their slopes and $y-$ intercepts.

If the slopes of the two lines are different, the lines are intersecting. They will cross each other at a single point, which can be found by solving the system of equations formed by the two lines.

If the slopes of the two lines are the same, but their $y-$ intercepts are different, the lines are parallel. They will never cross each other and will maintain the same distance between them.

If the slopes of the two lines are the same and their $y-$ intercepts are also the same, the lines are coincident, meaning they are the same line. In this case, they will have infinitely many points in common.

By analyzing the slopes and $y-$ intercepts of two lines, you can determine whether they are intersecting, parallel, or coincident.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.