Linear Equations - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Simplifying expressions Expanding expressions Combining like terms

Math resources Algebra Math equations

Linear equations

Here you will learn about linear equations, including how to graph linear equations and how to solve linear equations.

Students will first learn about linear equations as part of expression and equations in $8th$ grade math and will continue to use them throughout high school.

What is a linear equation?

A linear equation is an algebraic equation that contains variables that have an exponent that is not higher than one. A linear equation is called linear because when you plot the graph of the linear function, it will make a straight line graph.

Examples of equations

$3 x-5=7$
$2 x+5 y=15$

Nonlinear equations are a type of equations where terms can have variables raised to powers other than one, or terms that are multiplied or divided.

Examples of nonlinear equations:

$x^2+y^2=1$
$\cfrac{1}{x}+\cfrac{1}{y}=2$

All linear equations have an equal sign, this means that everything on the left-hand side of the sign is exactly the same as everything on the right-hand side.

The linear equation formula is the way of expressing a linear equation and can be done in various ways, depending on the number of variables present.

Standard form
Slope-intercept form of a linear equation
Point slope form of a linear equation

The standard form is $ax+by=c,$ where $a, b$ and $c$ are constants.

For example,

$\begin{aligned}& 2x-3y+4=0 \\\\ &3y-7x=8 \\\\ &4x=12 \end{aligned}$

Slope-intercept form

The slope-intercept form of a linear equation can be written as $y=mx+b,$ where $m$ is the slope of a line and $b$ is the $y$ -intercept.

Point slope form

The point slope form of a linear equation can be written as $y-y_1=m\left(x-x_1\right),$ where $m$ is the slope of the line and $\left(x_1, y_1\right)$ is a point on the line.

Graphing linear equations

Linear equations are related to coordinate grids, as they provide a way to graphically represent and solve linear equations.

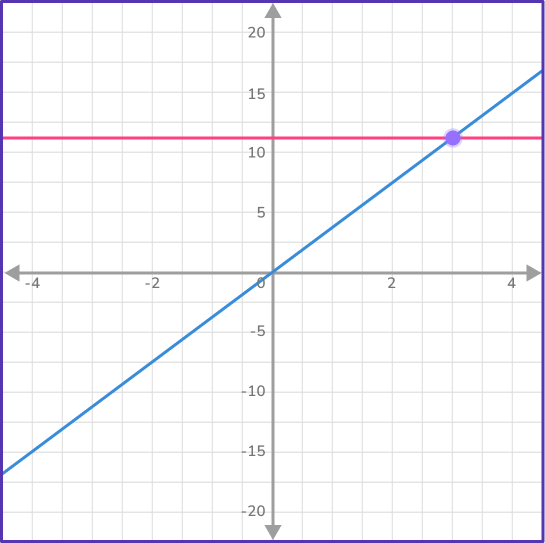
For example,

Given the equation

$\begin{aligned}&2x-3y+4=0 \\\\ &3y-7x=8 \\\\ &4x=12\end{aligned}$

we can graphically represent this equation on a coordinate grid

A one variable linear equation with the variable $x$ forms a vertical line that is parallel to the $y$ -axis.

For example,

Given the equation $x-4=0$

You need to isolate the variable by adding $4$ to both sides of the equation.

$\begin{aligned}& x-4=0 \\\\ & +4+4 \\\\ & x=4\end{aligned}$

To graph the line $x=4,$ you will draw a straight, vertical line through point $(4,0).$

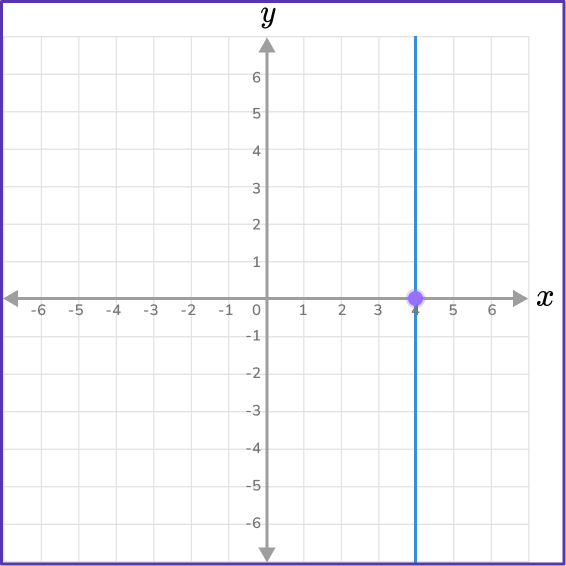
The slope in a vertical line is undefined.

A one variable linear equation with the variable $y$ forms a horizontal line that is parallel to the $y$ -axis.

For example,

Given the equation $y+6=0$

You need to isolate the variable by subtracting $6$ from both sides of the equation.

$\begin{gathered}y+6=0 \\\\ -6-6 \\\\ y=-6\end{gathered}$

To graph the line $y=-6,$ you will draw a straight, vertical line through point $(0,-6).$

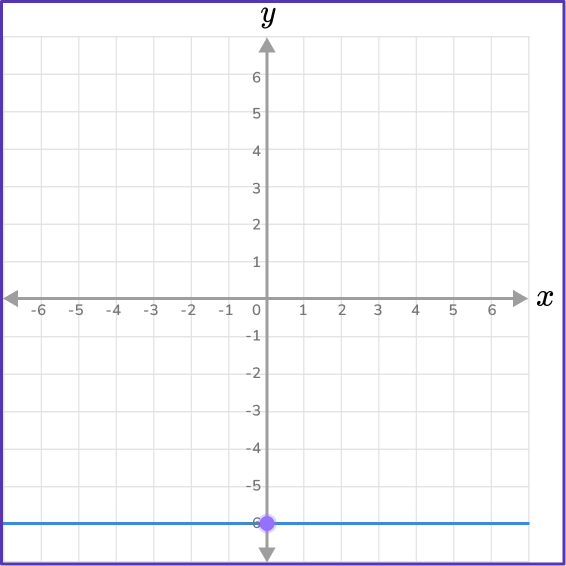
The slope in a horizontal line is $0.$

What is a linear equation?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8: Expressions and Equations (8.EE.C.7)
Solve linear equations in one variable.

a. Give examples of linear equations in one variable with one solution, infinitely many solutions, or no solutions. Show which of these possibilities is the case by successively transforming the given equation into simpler forms, until an equivalent equation of the form $x = a, a = a,$ or $a = b$ results (where $a$ and $b$ are different numbers).

b. Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.

High School: Algebra – Reasoning with Equations and Inequalities (HSA.REI.B.3)
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.

[FREE] Linear Equations Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of linear equations. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Linear Equations Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of linear equations. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to solve linear equations

In order to solve a linear equation, you will need to:

Simplify both sides of the equation.
Isolate the variable on one side of the equation.
Solve for the variable.

Linear equation examples

Example 1: linear equation with one unknown

Solve $3 x+6=18.$

Simplify both sides of the equation.

Both sides of the equation are simplified.

2Isolate the variable on one side of the equation.

Here, the opposite of $+6$ is $-6.$

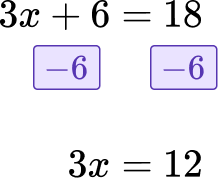
3Solve for the variable.

Here,

$3 x=3\times x,$ so divide by $3.$

$x=4$

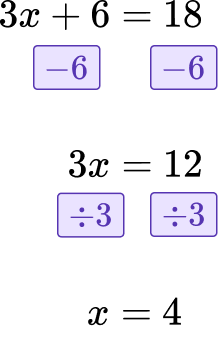
Example 2: linear equation with an unknown on both sides

Solve $5 x+6=2 x+9.$

Simplify both sides of the equation.

Here, $2x$ is smaller than $5x,$ so eliminate it by $-2x.$

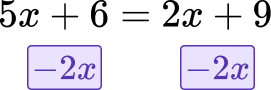
Isolate the variable on one side of the equation.

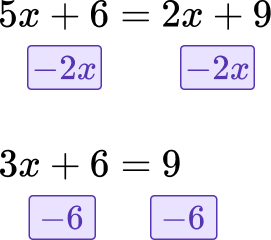
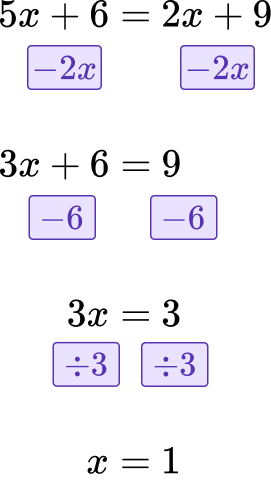
Solve for the variable.

Here,

$3x=3\times x,$ so we divide by $3.$

Example 3: linear equation with an unknown on both sides

Solve $-3 x-11=-12 x+16.$

Simplify both sides of the equation.

Here $-3x$ is smaller than $-12x,$ so eliminate it by adding $3x$ to both sides.

$\begin{aligned} -3 x-11&=-12 x+16 \\\\ +3 x \hspace{0.2cm} & \hspace{0.5cm}+3 x \\\\ -11&=-9 x+16\end{aligned}$

Isolate the variable on one side of the equation.

To isolate the variable, subtract $16$ from both sides of the equal sign.

$\begin{aligned} -11&=-9 x+16 \\\\ -16 & \hspace{0.5cm}-16 \\\\ -27&=-9 x\end{aligned}$

Solve for the variable.

To solve for the variable, divide each side by $-9.$

$\begin{aligned} -27&=-9 x \\\\ \div(-9) & \hspace{0.2cm} \div(-9) \\\\ x&=3\end{aligned}$

Example 4: solve a linear equation with parentheses

Solve $4(x-2)=12.$

Simplify both sides of the equation.

Start by distributing the $4$ to the factors within the parentheses.

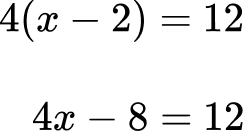
Isolate the variable on one side of the equation.

Here the opposite of $-8$ is $+8,$ so you will add $8$ to both sides.

$\begin{aligned}4 x-8&=12 \\\\ +8 & \hspace{0.3cm} +8 \\\\ 4 x&=20\end{aligned}$

Solve for the variable.

Because $4x=4\times x,$ divide by $4$ to solve for the variable.

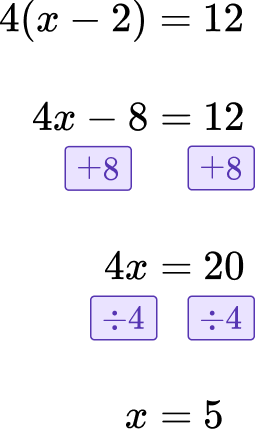
Example 5: linear equation with parentheses

Solve $-2(4 x+10)=12.$

Simplify both sides of the equation.

Start by distributing the $-2$ to the factors within the parentheses.

$\begin{aligned}& -2(4 x+10)=12 \\\\ & -8 x-20=12\end{aligned}$

Isolate the variable on one side of the equation.

The opposite of $-20$ is $+20,$ so you will add $20$ to both sides.

$\begin{aligned}-8 x-20&=12 \\\\ +20 & \hspace{0.2cm} +20 \\\\ -8 x&=32\end{aligned}$

Solve for the variable.

To solve for the variable, we will divide both sides of the equation by $-8.$

$\begin{aligned}-8 x& =32 \\\\ \div(-8) & \hspace{0.2cm} \div(-8) \\\\ x&=4\end{aligned}$

Example 6: linear equation with fractions

Solve $\cfrac{5 x-2}{4}=\cfrac{2 x+2}{2} \, .$

Simplify both sides of the equation.

Cross multiply, by multiplying each fraction by the denominator on the other side of the equal sign to get rid of the fractions.

$\begin{aligned}& (5 x-2) \times(2)=(2 x+2) \times(4) \\\\ & 10 x-4=8 x+8\end{aligned}$

Isolate the variable on one side of the equation.

Start by subtracting $8x$ from both sides of the equation.

$\begin{aligned} 10 x-4&=8 x+8 \\\\ - \, 8 x \hspace{0.1cm} & \hspace{0.2cm}-8 x \\\\ 2 x-4&=8\end{aligned}$

Then add $4$ to both sides of the equation.

$\begin{aligned}2 x-4&=8 \\\\ +4 \hspace{0.1cm} & \hspace{0.2cm} +4 \\\\ 2 x&=12\end{aligned}$

Solve for the variable.

Solve for $x$ by dividing both sides of the equation by $2.$

$\begin{aligned} 2 x & =12 \\\\ \div 2 & \hspace{0.2cm} \div 2 \\\\ x&=6\end{aligned}$

Teaching tips for linear equations

Ensure students have a solid understanding of contents, variables, coefficients and terms before beginning linear equations.

Use visual aids like graphs to help students understand the relationship between linear equations and lines. Show them how to plot linear equations on a coordinate plane and interpret the slope and $y$ -intercept.

Mistakes are opportunities to reinforce learning. Encourage students to make mistakes, as errors in problem solving can lead to class discussions about the mistakes and how to solve them.

Easy mistakes to make

Not simplifying both sides of the equations
Both sides of the equal sign $(=)$ must be simplified in order to solve the equation correctly. For example, in order to simplify the equation below, you would subtract two from both sides of the equal sign.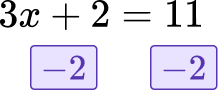

Making errors when using the distributive property
When distributing a number to multiple terms, make sure to multiply by all of the numbers within parenthesis. For example, $5(x+6),$ you would multiply the $5$ by both $x$ and $6.$

Math equations
Rearranging equations
How to find the equation of a line
Solving equations
Writing linear equations
Substitution
One step equations
Identity math
Solve equations with fractions

Practice linear equations problems

x=14

x=8

x=6

x=10

$2 x+8=20$

First, subtract $8$ from both sides.

$2 x=12$

Solve for the variable by dividing both sides by $2.$

$x=6$

x=5

x-8

x=-12

x=3

$5 x-3=12$

First, add $3$ to both sides.

$5 x=15$

Then divide both sides by $5.$

$x=3$

x=7

x=12

x=-7

x=4

$2 x-7=x+5$

First, subtract $x$ from both sides.

$x-7=5$

Then add $7$ to both sides to solve for the variable.

$x=12$

x=6

x=4

x=7

x=3

$7 x-3=4 x+15$

Start by subtracting $4x$ from both sides.

$3 x-3=15$

Then add $3$ to both sides.

$3 x=18$

To solve for the variable, divide both sides by $3.$

$x=6$

x=2

x=3

x=5

x=-3

$5(x-3)=10$

Start by dividing both sides by $5.$

$x-3=2$

Add $3$ to both sides of the equal sign to solve for $x.$

$x=5$

x=3

x=-13

x=-5

x=13

$3(x-3)=6(x+5)$

Start by distributing within the parenthesis.

$3 x-9=6 x+30$

Then, subtract $3x$ from both sides.

$-9=3 x+30$

Subtract $30$ from both sides.

$-39=3 x$

To solve for the variable, divide both sides by $3.$

$x=-13$

x=-2

x=2

x=-1

x=1

$\cfrac{3x+1}{2}+\cfrac{2x-2}{4}$

Cross multiply, by multiplying each fraction by the denominator on the other side of the equal sign to get rid of the fractions.

$(3 x+1) \times 2=(2 x-2) \times 4$

$12x+4=4x-4$

From both sides of the equation, subtract $4x$ .

$8x+4=-4$

and subtract $-4$

$8x=-8$

Finally divide by $8.$

$x=-1$

Linear equation FAQs

Can a linear equation have more than one solution?

Yes, a linear equation in two variables can have an infinite amount of solutions. The solutions are all of the points that lie on the line represented by the given equation.

What are simultaneous linear equations?

Simultaneous linear equations are a system of linear equations, two or more, with two or more variables. Solving such systems involves finding values for the variables that satisfy all the equations simultaneously.

See also: Systems of linear equations

How is the quadratic equation related to linear equations?

Quadratic equations are an extension of linear equations, representing a more complex relationship between variables. Linear equations create straight lines, while quadratic equations create a parabola, or a $U$ -shaped curve.

What is the general form of linear equations?

The general form of linear equations is another way to say “standard form”. The standard form, or general form, is $ax+by=c,$ where $a, b$ and $c$ are constants.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.