[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Independent and dependent variables
Interpreting graphs Linear graphHow to find the equation of a line
Here you will learn about how to find the equation of a line, including y=mx+b, recognizing the slope and y- intercept of a straight line, and finding the equation of a line given the graph.
Students will first learn about how to find the equation of a line as part of equations and expressions in 8 th grade and will expand on their knowledge in high school.
What is the equation of a line?
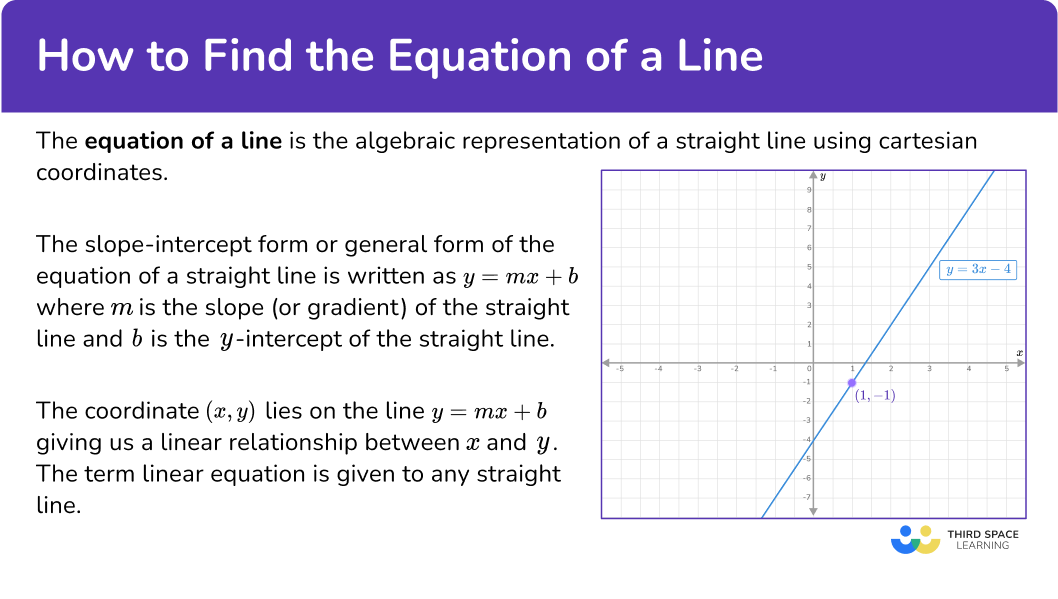
The equation of a line is the algebraic representation of a straight line using cartesian coordinates.
The slope-intercept form or general form of the equation of a straight line is written as y=mx+b where m is the slope (or gradient) of the straight line and b is the \textbf{y-} intercept of the straight line.
The slope represents the slant of the line and the y- intercept is the point where the line crosses the y- axis.
The coordinate (x,y) lies on the line y=mx+b giving us a linear relationship between x and y. The term linear equation is given to any straight line.
For example,
Look at the line y=3x-4.
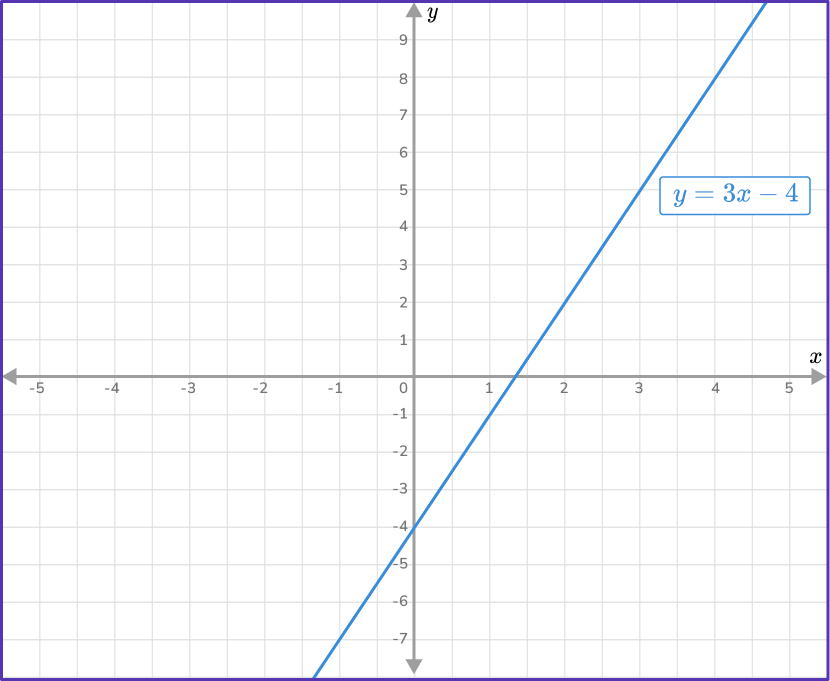
Here, you can find any y- coordinate given the value for x by substituting into the equation y=3x-4.
For example, when x=1,
\begin{aligned} y&=3\times{1}-4\\\\ y&=3-4\\\\ y&=-1 \end{aligned}When the x value is 1 and the y value is -1, this gives the coordinate (1,-1) which lies on the line as shown below.
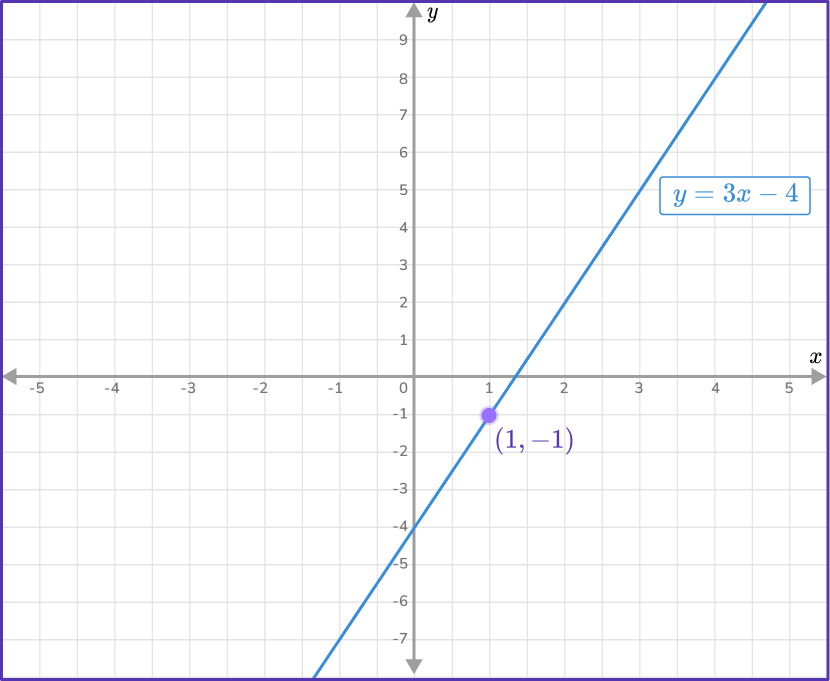
Not all straight lines will appear to be exactly in the form y=mx+b , so you need to understand how we determine the gradient (or slope of the line) m and the y- intercept of the line (the point where the line intersects the y- axis) b from equations that are not in the form y=mx+b.
Examples of linear equations not in the slope-intercept form of general form y=mx+b\text{:}
- y+17=6x
- 2y=10x+3
- x=6y-1
- y=-3 (a horizontal line)
- x=y
- x=0 (a vertical line)
All of the equations above can be graphed as straight lines but none are explicitly written in the slope-intercept form y=mx+b.
In order to easily determine m and b , we need to rearrange the equation to make y the subject.
For example,
Take the equation above of y+17=6x and make y the subject.
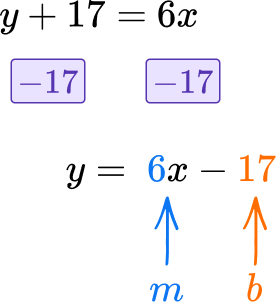
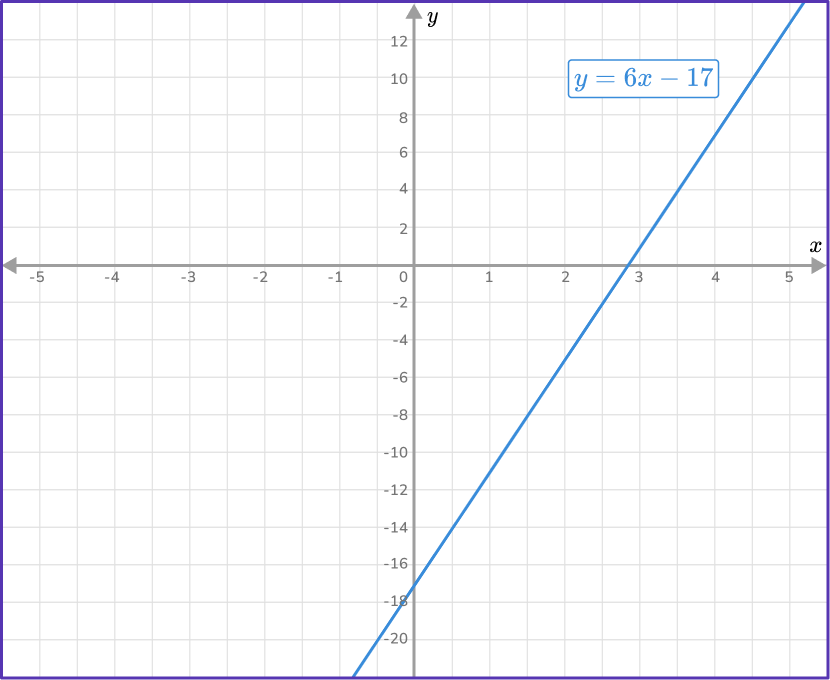
By rearranging the equation into the form y=mx+b, it clearly identifies the slope, m=6, and the y- intercept, b=-17.
From this information, you can sketch the straight line on the cartesian plane or the xy \, - plane.
What is the equation of a line?
Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8: Expressions and Equations (8.EE.B.5)
Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. For example, compare a distance-time graph to a distance-time equation to determine which of two moving objects has greater speed.
- Grade 8: Expressions and Equations (8.EE.B.6)
Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y=mx for a line through the origin and the equation y=mx+b for a line intercepting the vertical axis at b.
![[FREE] Math Equations Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Equations Worksheet (Grade 6 to 8)
![[FREE] Math Equations Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of math equations. 10+ questions with answers covering a range of 6th, 7th and 8th grade math equations topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Math Equations Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Equations Worksheet (Grade 6 to 8)
![[FREE] Math Equations Worksheet (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of math equations. 10+ questions with answers covering a range of 6th, 7th and 8th grade math equations topics to identify areas of strength and support!
DOWNLOAD FREEHow to find the equation of a line
In order to find the equation of a line:
- Find the slope of the line.
- State the \textbf{y-} intercept of the straight line.
- Write the equation of the line in the form \textbf{y = mx + b}.
How to find the equation of a line examples
Example 1: positive slope, positive y- intercept
Work out the equation of the straight line given in the diagram below.
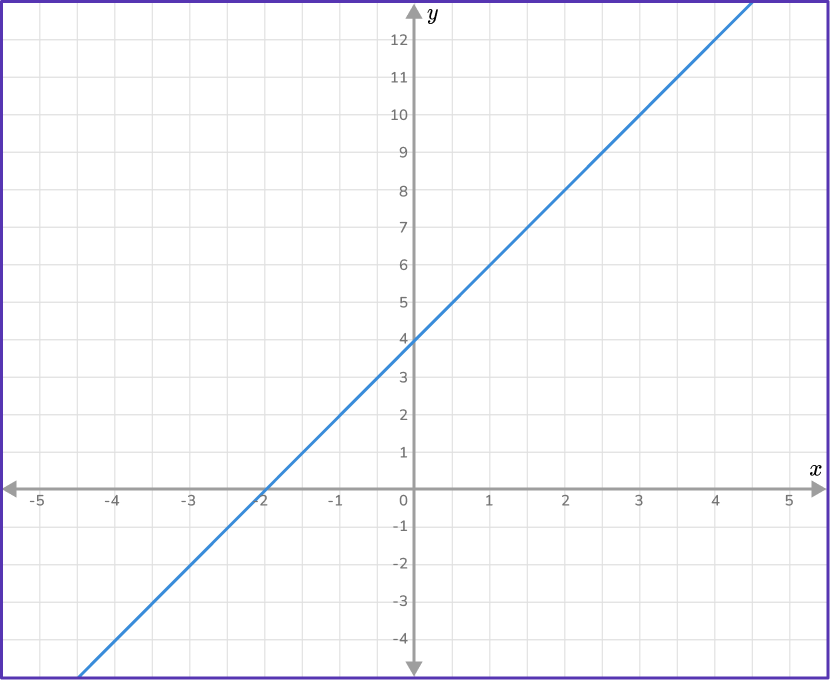
- Find the slope of the line.
Two points that lie on the line are: (0,4) and (2,8). The line passes through these two given points. As you are given two points on the line, use the slope formula to find m.
Slope formula: m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{8-4}{2-0}=\cfrac{4}{2}=2
m=2The slope of this line is 2.
2State the \textbf{y-} intercept of the straight line.
The y- intercept occurs when x=0. From the graph, you can see that when x=0, y=4.
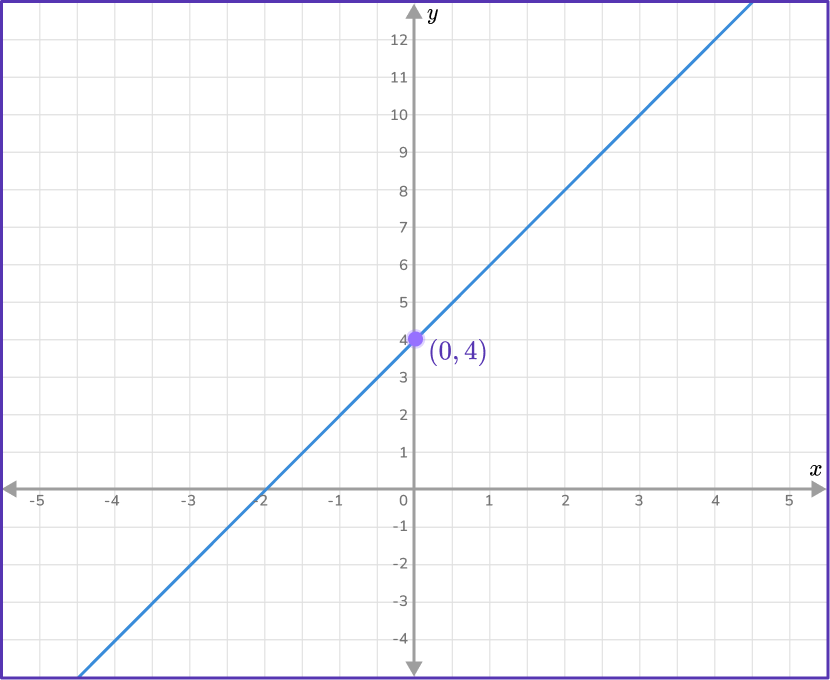
So, b=4.
3Write the equation of the line in the form \textbf{y = mx + b}.
Since the slope m=2 and y- intercept b=4, you can substitute 2 for m and 4 for b, y=2x+4.
Example 2: positive slope, negative y- intercept
Work out the equation of the straight line given in the diagram below.
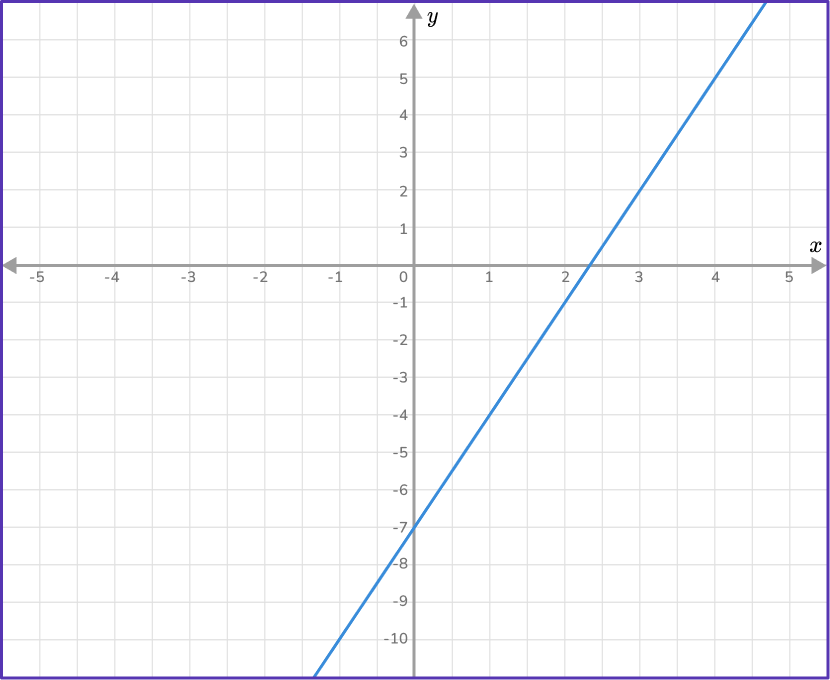
Find the slope of the line.
Two points that lie on the line are: (1,-4) and (3,2). As you are given two points on the line, use the slope formula to find m.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{2--4}{3-1}=\cfrac{6}{2}=3
m=3
State the \textbf{y-} intercept of the straight line.
The y- intercept is the point where x=0. From the graph, when x=0, you can see that y=-7. So, the y- intercept is -7, \, b=-7.
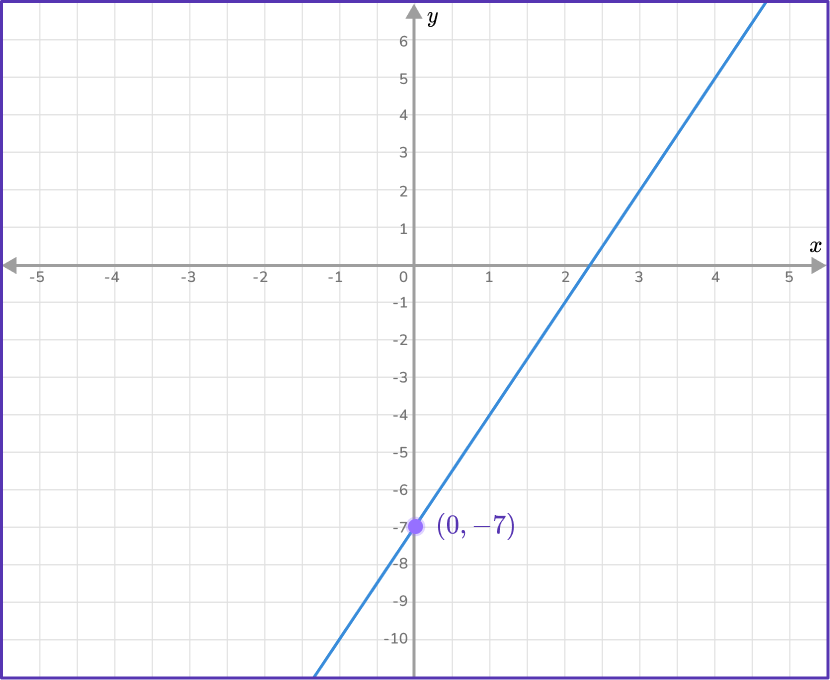
Write the equation of the line in the form \textbf{y = mx + b}.
Since, m=3 and b=-7, you can substitute 3 for m and -7 for b, \, y=3x-7.
Example 3: negative gradient, positive y- intercept
Work out the equation of the straight line given in the diagram below.
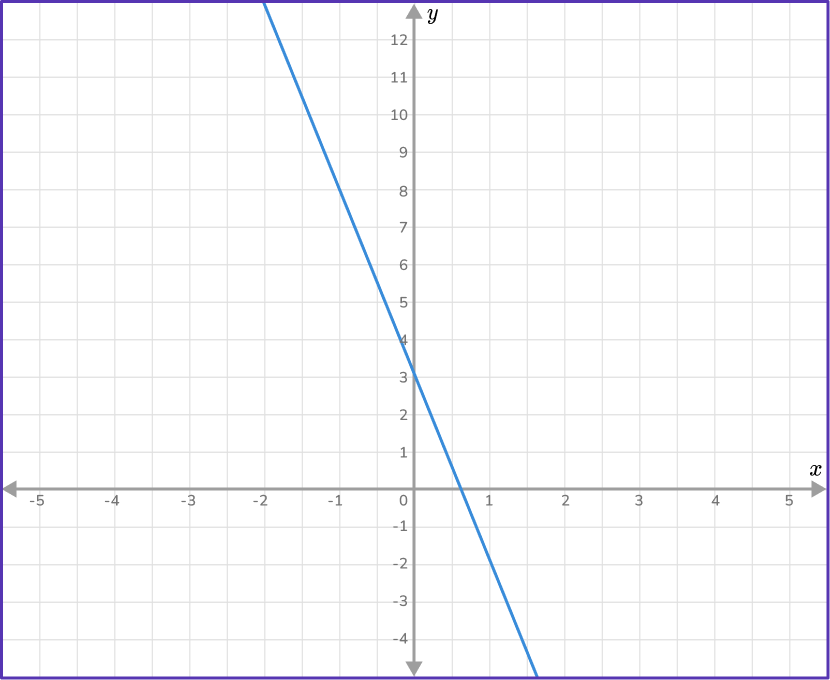
Find the slope of the line.
Two points that lie on the line are: (1,-2) and (-1,8). As you are given two points on the line, use the slope formula to find m.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{8--2}{-1-1}=\cfrac{10}{-2}=-5
m=-5
State the \textbf{y-} intercept of the straight line.
The y- intercept occurs when x=0. From the graph you can see that when x=0, y=3. So the y- intercept is 3, \, b=3.
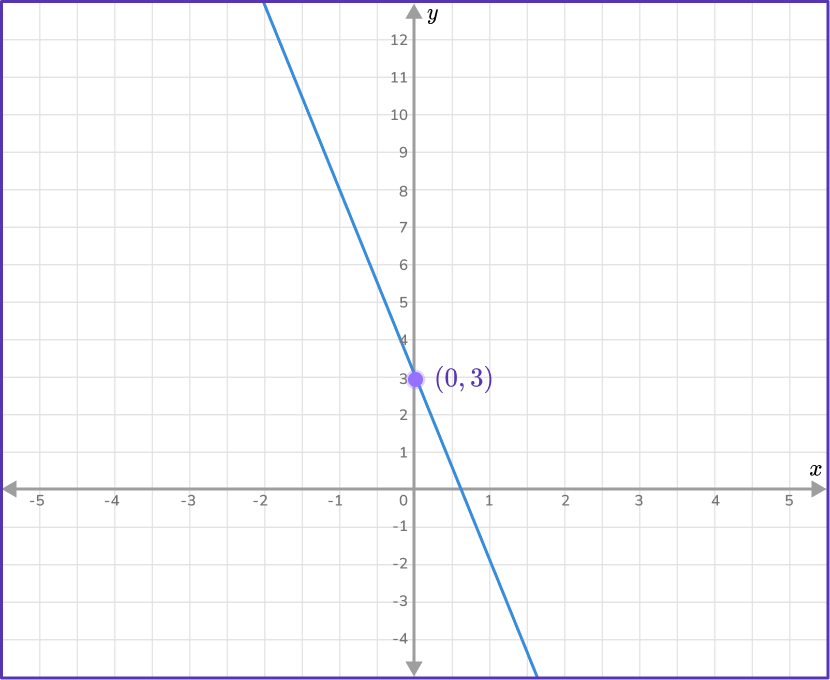
Write the equation of the line in the form \textbf{y = mx + b}.
Since, m=-5 and b=3, you can substitute -5 for m and 3 for b, \, y=-5x+3.
Example 4: negative slope, negative y- intercept
Work out the equation of the straight line given in the diagram below.
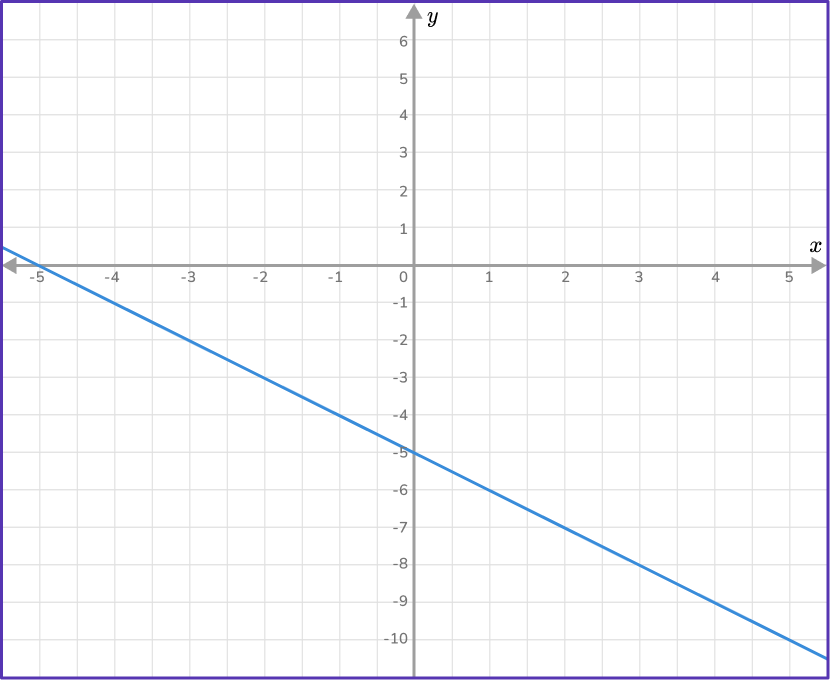
Find the slope of the line.
Two points that lie on the line are: (-3,-2) and (2,-7). As you are given two points on the line, use the slope formula to find m.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{-7--2}{2--3}=\cfrac{-5}{5}=-1
m=-1
State the \textbf{y-} intercept of the straight line.
The y -intercept occurs when x=0. From the graph, you can see that when x=0, \, y=-5. So, the y -intercept is -5, \, b=-5.
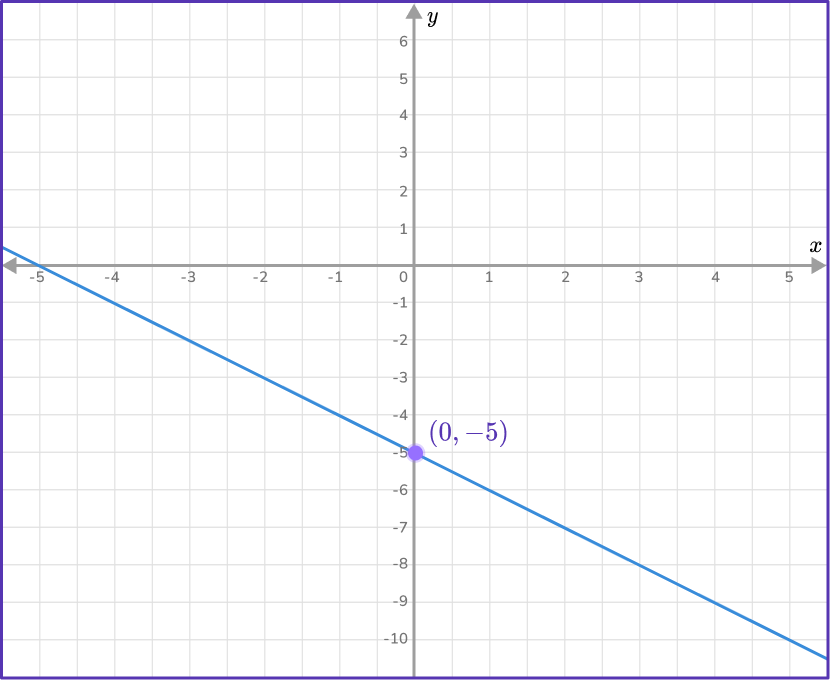
Write the equation of the line in the form \textbf{y = mx + b}.
Since m=-1 and b=-5, you can substitute -1 for m and -5 for b, \, y=-x-5.
Example 5: positive fractional slope, positive y- intercept
Work out the equation of the straight line given in the diagram below.
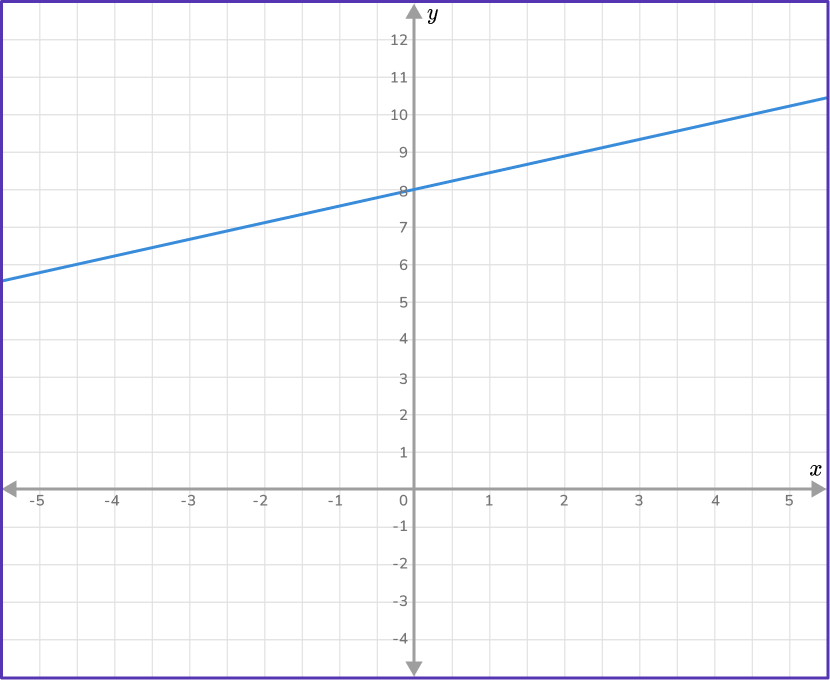
Find the slope of the line.
Two points that lie on the line are: (4,10) and (-2,7). As you are given two points on the line, use the slope formula to find m.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{7-10}{-2-4}=\cfrac{-3}{-6}=\cfrac{1}{2}
m=\cfrac{1}{2}
State the \textbf{y-} intercept of the straight line.
The y- intercept occurs when x=0. From the graph, when x=0, \, y=8, so the y- intercept is 8, \, b=8.
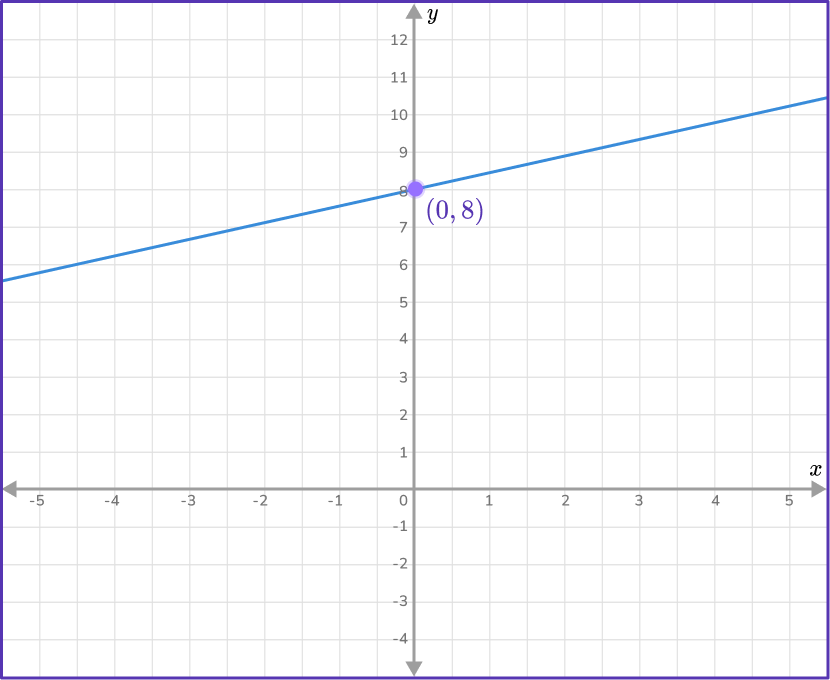
Write the equation of the line in the form \textbf{y = mx + b}.
Since m=\cfrac{1}{2} and b=8, you can substitute \cfrac{1}{2} for m and 8 for b, \, y=\cfrac{1}{2}x+8.
Example 6: negative fractional slope, negative y- intercept
Work out the equation of the straight line given in the diagram below.
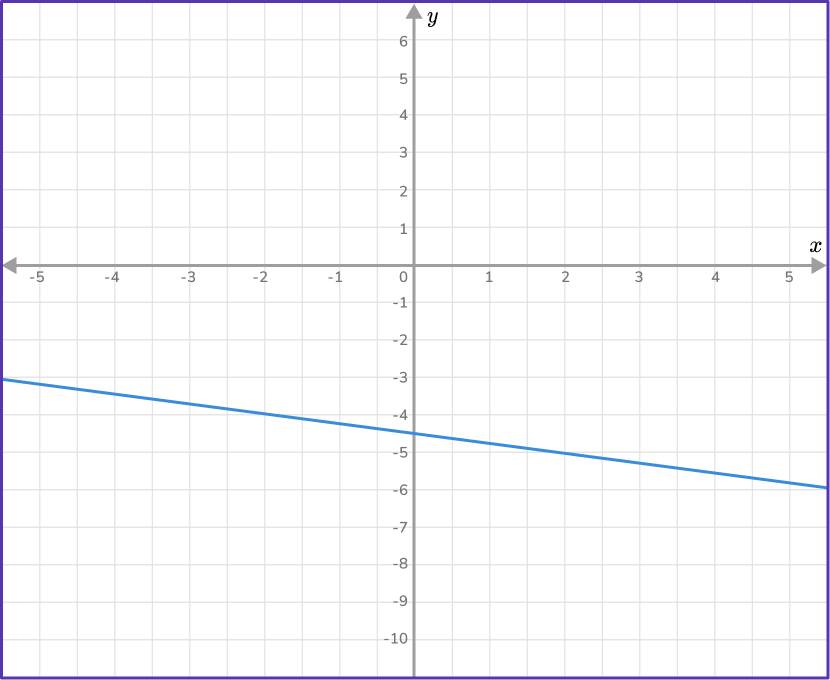
Find the slope of the line.
Two points that lie on the line are: (-2,-4) and (2,-5). As you are given two points on the line, use the slope formula to find m.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{-5--4}{2--2}=\cfrac{-1}{4}
m=\cfrac{-1}{4}
State the \textbf{y-} intercept of the straight line.
The y- intercept occurs when x=0. From the graph, when x=0, \, y=-4.5 so the y- intercept is -4.5, \, b=-4.5 or -\cfrac{9}{2}.
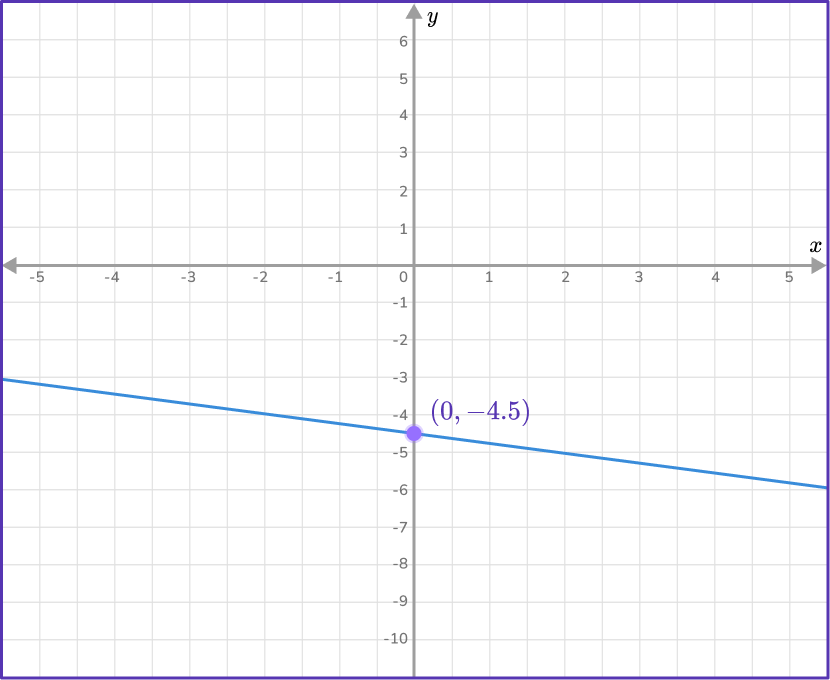
Write the equation of the line in the form \textbf{y = mx + b}.
Since m=-\cfrac{1}{4} and b=-\cfrac{9}{2}, you can substitute -\cfrac{1}{4} for m and -\cfrac{9}{2} for b, \, y=-\cfrac{1}{4}x-\cfrac{9}{2}.
Teaching tips for how to find the equation of a line
- Ensure that students have a solid understanding of the basics, including the slope-intercept form of a line (y=mx+b), where m is the slope and b is the y- intercept.
- Provide students with various problems that increase with difficulty, starting with simple examples and gradually getting more challenging. Allowing students the ability to work on these problems both collaboratively and independent allows for differentiation.
Easy mistakes to make
- Mixing up the slope and the \textbf{y-} intercept
The coefficient of x is the slope m and the constant term is the y- intercept b. If the coefficient of x is 1, remember this is written as x only as 1x=x.
- The slope can be positive or negative
Ignoring the negative values in a coordinate means that the slope will be calculated incorrectly. When picking two ordered pairs, make sure that the coordinates go through the corner of a grid square. If there are negative values, make sure you use them with the negative symbol.
- Mixing up the coordinates
When finding the slope of a straight line, make sure you always use one coordinate first, and not mix them up. For example, looking back at example 5, we have the two points that lie on the line being (1,-2) and (-1,8). The change in y is calculated as 8--2 and the change in x is calculated as 1--1.
Here, the coordinates have been mixed up when completing the subtraction. This would result in the slope of the line being 5 and not -5.
Correct answer: m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{8--2}{-1-1}=\cfrac{10}{-2}=-5
- Incorrect change in \textbf{x} or \textbf{y}
Avoid counting squares to work out the change in x or y. Use the axes scales or label the coordinates, then find the difference between them.
- Not writing an equation
Taking example 1, the student looks at the y- intercept and determines the line x+4. This may work when x=0 but not for any other value for x.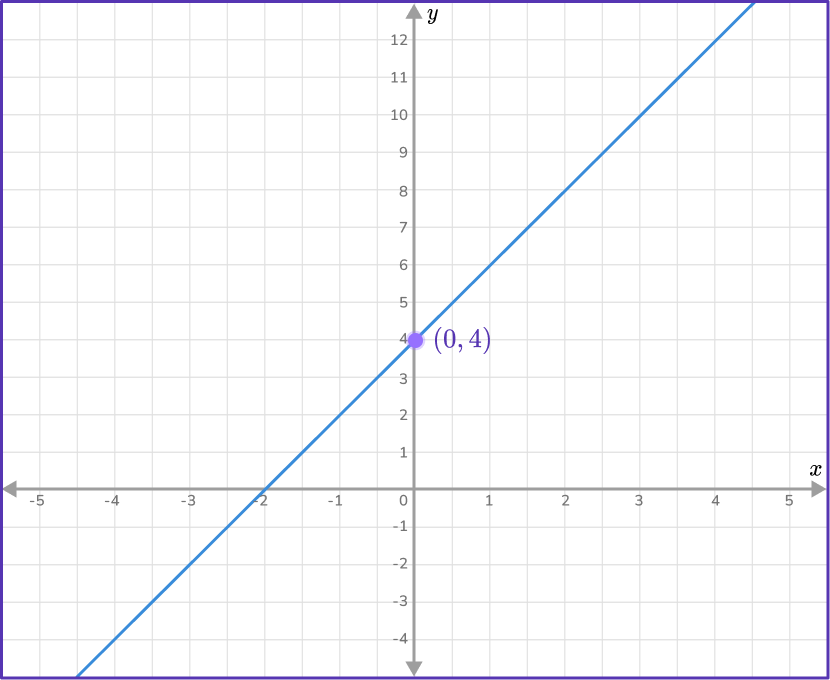
Related math equations lessons
- Rearranging equations
- Linear equations
- Identity math
- Substitution
- One step equations
- Solve equations with fractions
- Writing linear equations
- Solving equations
Practice equation of a line questions
1. Find the equation of the line in the form y=mx+b.
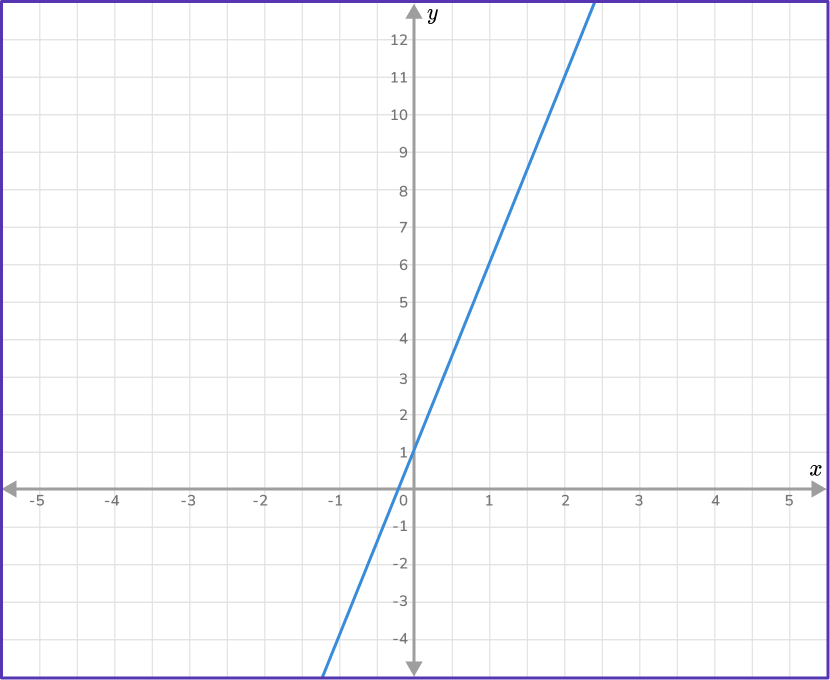




Two coordinates: (0,1) and (2,11)
m=\cfrac{11-1}{2-0}=\cfrac{10}{2}=5
b=1
2. Write the equation of the line in slope-intercept form.
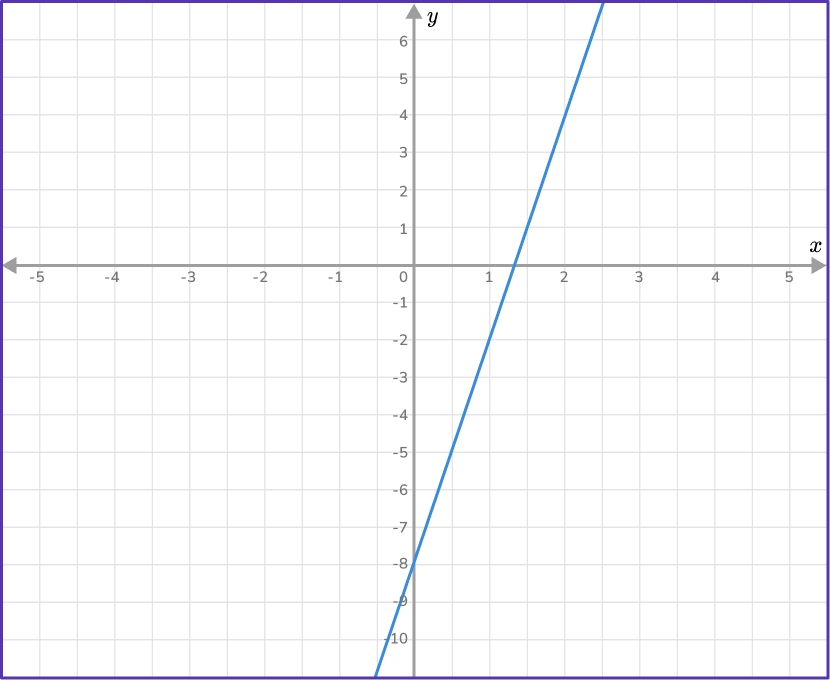




Two coordinates: (0,-8) and (1,-2)
m=\cfrac{-2- -8}{1-0}=\cfrac{6}{1}=6
b=-8
3. Find the equation of the line in slope-intercept form.
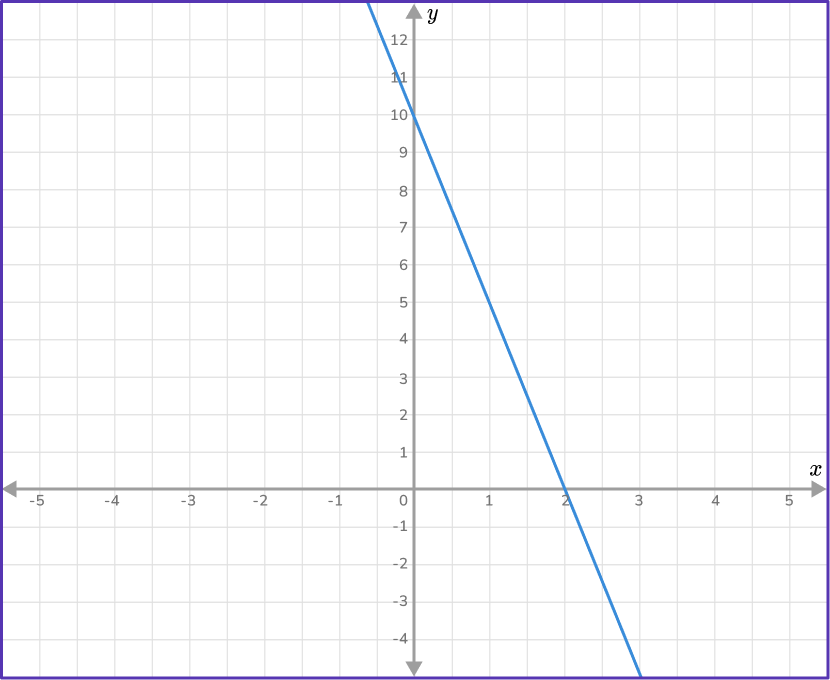




Two coordinates: (2,0) and (1,5)
m=\cfrac{5-0}{1-2}=\cfrac{5}{-1}=-5
b=10
4. Write the equation of the line in y=mx+b form.
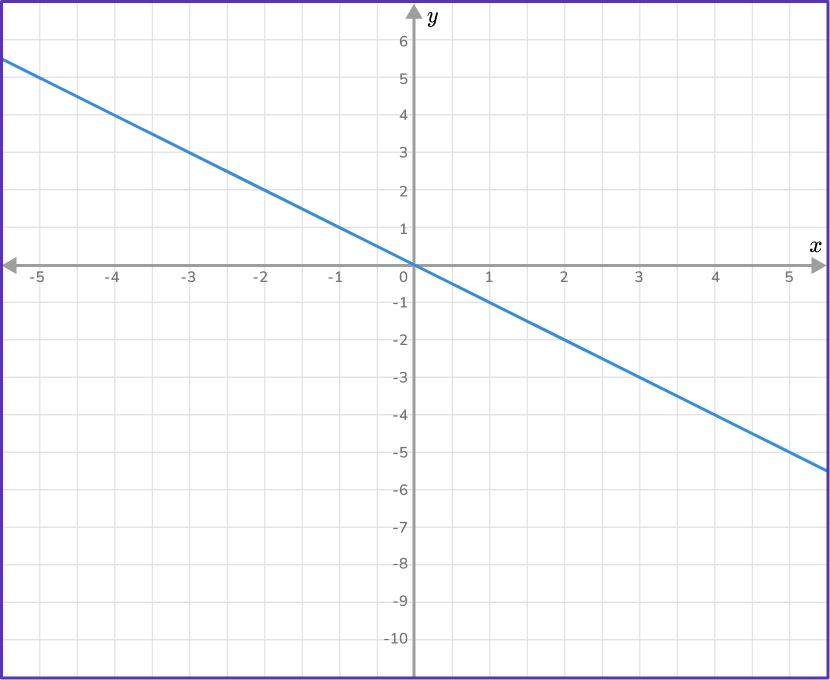




Two coordinates: (3,-3) and (4,-4)
m=\cfrac{-4- -3}{4-3}=\cfrac{-1}{1}=-1
b=0
5. Find the equation of the line in slope intercept form.
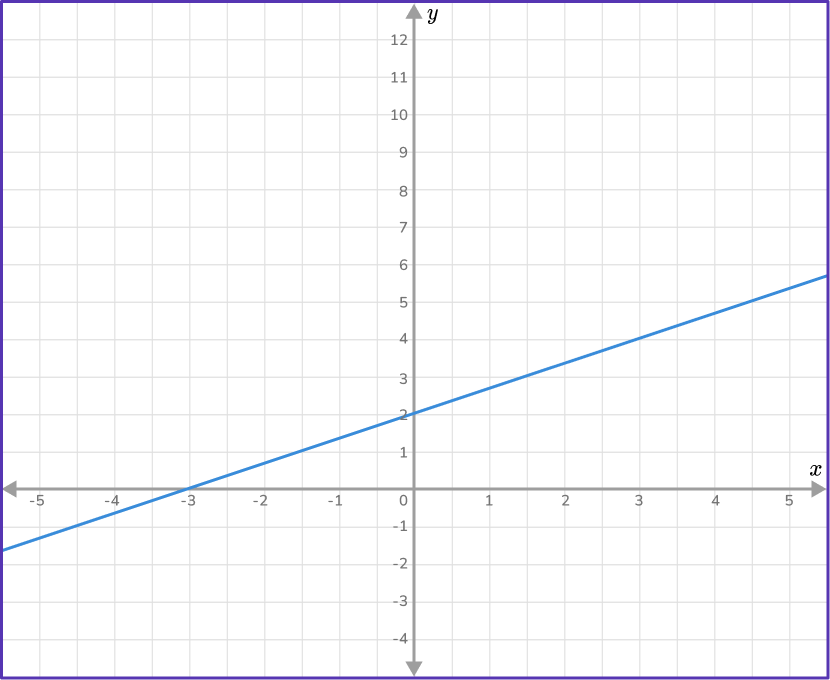




Two coordinates: (0,2) and (3,4)
m=\cfrac{4-2}{3-0}=\cfrac{2}{3}
b=2
6. Write the equation of the line in y=mx+b form.
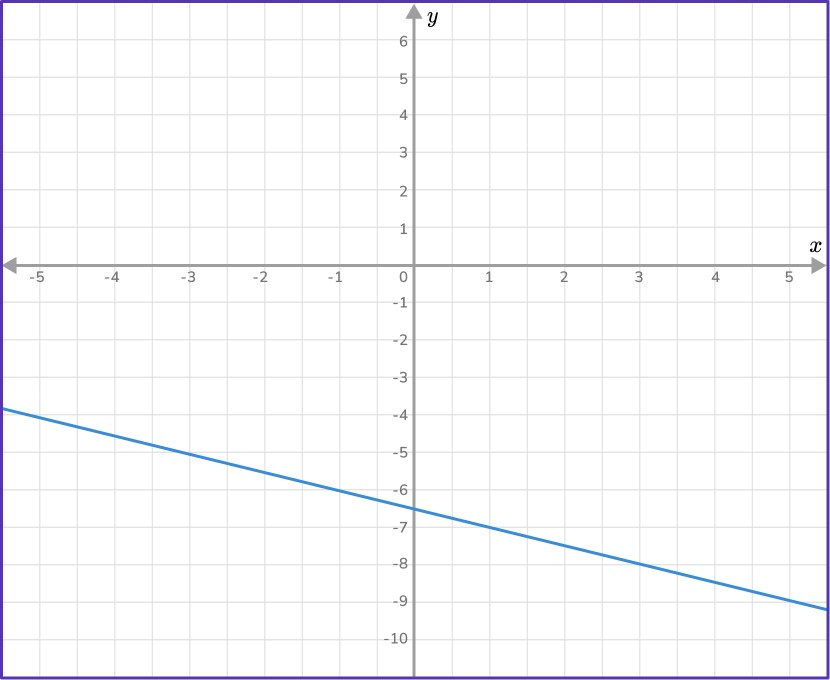




Two coordinates: (3,-8) and (-3,-5)
m=\cfrac{-5- -8}{-3-3}=\cfrac{3}{-6}=-\cfrac{1}{2}
b=-\cfrac{13}{2}
Equation of a line FAQs
In order to find the slope of a line, you need either two points on the line or have the information needed to find the rise over run between two points on the line.
The point-slope formula is used when you have a point on a line and it’s given slope. The point-slope equation is y-y_{1}=m\left(x-x_1\right), where \left(x_1, y_1\right) is a point on the line and m is the slope.
The x- intercept of a line is a point on a graph that intersects the x- axis. The x- coordinate will be the point that intersects the x- axis, and the y- coordinate will be 0.
Yes, you can find the slope of both parallel lines. Parallel lines will have the same slope, even if they are at different positions on the coordinate plane.
Yes, you can find the slope of both perpendicular lines. Perpendicular lines have slopes that are negative reciprocals of each other. You can determine the slope of two perpendicular lines by using m_{1}\times{m}_{2}=-1.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!