GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Rounding to the nearest 10,100 and 1000 Rounding decimals Significant figures Place value InequalitiesThis topic is relevant for:

How To Calculate Upper And Lower Bounds
Here we will learn about how to calculate upper and lower bounds, including finding the place value of the given degree of accuracy, calculating upper and lower bounds and writing error intervals.
There are also how to calculate upper and lower bounds worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are upper and lower bounds?
The upper and lower bounds of a rounded number are the biggest and smallest values that the number could have been before it was rounded.
We often round numbers to a given degree of accuracy, for example to the nearest 10 or to 1 decimal place.
To work out the upper and lower bounds of a rounded number, we need to think about the degree of accuracy the number has been rounded to.
For example,
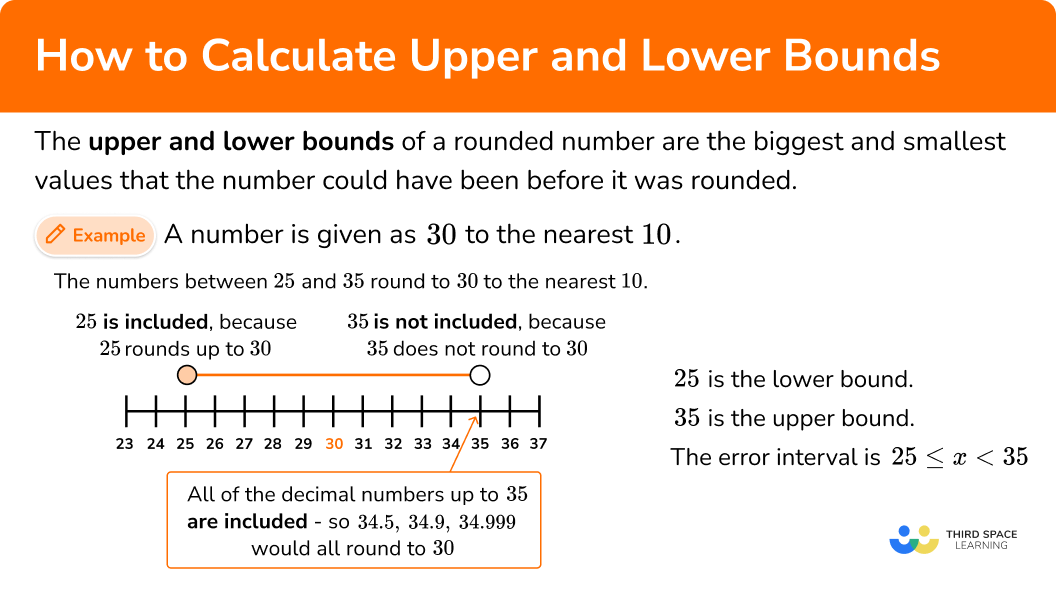
A number is given as 30 to the nearest 10 .
Find the upper and lower bounds of the number.
We need to consider numbers both smaller and bigger than 30 that will round to 30 .
If we consider numbers that would round up to 30 , we realise that 29, 28, 27, 26 and 25 would all round to 30 to the nearest 10 .
25 is the minimum value that would round up to 30 , therefore the lower bound when 30 is rounded to the nearest 10 is \bf{25} .
If we consider numbers that would round down to 30 , we realise that 31, 32, 33 and 34 would all round to 30. \; 35 would round up to 40. However, we need to be careful here as 34.5 or 34.9 or even 34.9999… would still round down to 30.
Therefore we say the upper bound when 30 is rounded to the nearest 10 is \bf{35} (as we can get infinitely close to 35 and still round down to 30 ).
All numbers between 25 and 35 would round to 30 to the nearest 10 .
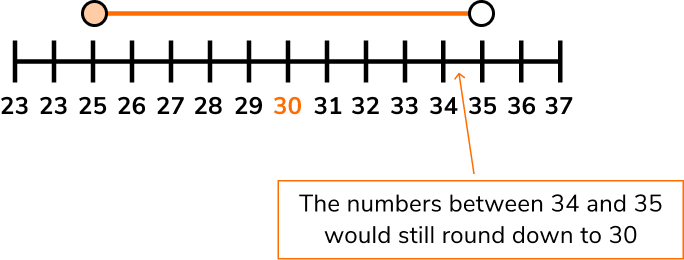
An error interval represents all the possible values that would round to the given value. In this example, the error interval is
25 \leq x < 35 .
Notice that the lower bound uses a \leq because 25 would round to 30 but the upper bound uses a < as 35 would not round to 30 but anything smaller than it would.
What are upper and lower bounds?
How to calculate upper and lower bounds
The following method can be used to calculate upper and lower bounds:
- Identify the place value of the degree of accuracy stated.
- Divide this place value by \bf{2}.
- Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
You can then use these to write an error interval:
\text{Lower bound } \leq x < \text{Upper bound}The error interval shows the range of values that the number could have taken before it was rounded.
Explain how to calculate upper and lower bounds

How to calculate upper and lower bounds worksheet

Get your free how to calculate upper and lower bounds worksheet of 20+ upper and lower bounds questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
How to calculate upper and lower bounds worksheet

Get your free how to calculate upper and lower bounds worksheet of 20+ upper and lower bounds questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEHow to calculate upper and lower bounds examples
Example 1: rounded to the nearest 100
A number is given as 600 to the nearest 100. Find the upper and lower bounds of the number.
- Identify the place value of the degree of accuracy stated.
In this example, the number has been rounded to the nearest 100 so the place value is 100.
2Divide this place value by \bf{2.}
100 \div 2=503Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 600 + 50 = \bf{650} .
The lower bound is 600-50 = \bf{550} .
This means that the original value could be anywhere between 550 and 650.
Example 2: rounded to the nearest whole number
A number is given as 14 to the nearest whole number. Work out the upper and lower bounds of the number and write down the error interval.
Identify the place value of the degree of accuracy stated.
The number here has been rounded to the nearest whole number so the place value is 1.
Divide this place value by \bf{2} .
Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 14+0.5=\bf{14.5} .
The lower bound is 14-0.5= \bf{13.5} .
The error interval is 13.5 \leq x < 14.5 .
Example 3: rounded to 1 decimal place
A number is given as 3.7 correct to 1 decimal place. Calculate the upper and lower bounds of the number.
Identify the place value of the degree of accuracy stated.
The number has been rounded to 1 decimal place so the place value is 0.1 (tenths).
Divide this place value by \bf{2} .
Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 3.7 + 0.05 =\bf{3.75} .
The lower bound is 3.7-0.05 = \bf{3.65} .
Example 4: rounded to 2 significant figures
A number is given as 470 to 2 significant figures. Work out the upper and lower bounds of the number.
Identify the place value of the degree of accuracy stated.
When we are given the degree of accuracy to a number of significant figures, we need to consider the place value more carefully. We look at the place value of the last significant figure.
In this example, we can see that the last significant figure is in the tens column so the place value is 10 .
Divide this place value by \bf{2} .
Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 470 + 5 =\bf{475} .
The lower bound is 470-5 = \bf{465} .
Example 5: rounded to 3 significant figures
A number is given as 7.32 correct to 3 significant figures. Calculate the upper and lower bounds of the number and write down the error interval.
Identify the place value of the degree of accuracy stated.
In this example, the last significant figure is in the hundredths column and so the place value is 0.01.
Divide this place value by \bf{2} .
Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 7.32+0.005 =\bf{7.325} .
The lower bound is 7.32-0.005 = \bf{7.315} .
The error interval is 7.315 \leq x < 7.325 .
Example 6: rounded to 2 significant figures
A number is given as 3000 to 2 significant figures. Work out the upper and lower bound of the number and write down the error interval.
Identify the place value of the degree of accuracy stated.
We need to be really careful with this one as it is rounded to 2 significant figures. The second significant figure is actually 0 and is in the hundreds column so the place value is 100.
Divide this place value by \bf{2} .
Add this amount to the given value to find the upper bound, subtract this amount from the given value to find the lower bound.
The upper bound is 3000 + 50 =\bf{3050} .
The lower bound is 3000-50= \bf{2950} .
The error interval is 2950 \leq x < 3050 .
Common misconceptions
- Using a value ending in \bf{4} for the upper bound
For example,
Stating 24 as the upper bound when a number is 20 to the nearest 10 .
Remember that there are numbers bigger than 24 that would round down to 20 such as 24.9. The upper and lower bounds (when rounding to a multiple of 10 ) should always end in 5 .
- Incorrectly identifying place value
For example,
Using the place value of 100 when a number is 700 to the nearest 10. It may appear that the number has been rounded to the nearest 100 when in fact it has been rounded to the nearest 10.
Related lessons on how to calculate upper and lower bounds
How to calculate upper and lower bounds is part of our series of lessons to support revision on rounding numbers, and upper and lower bounds. You may find it helpful to start with the main rounding numbers lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice how to calculate upper and lower bounds questions
1. A number is given as 4000 correct to the nearest 1000. Calculate the upper and lower bounds of the number.
Upper bound 4499 , lower bound 3500

Upper bound 4400 , lower bound 3500

Upper bound 4500 , lower bound 3500

Upper bound 4050 , lower bound 3950

The place value here is 1000.
1000 \div 2 =500 4000+500=4500, \; 4000-500=3500
2. A number is given as 600 correct to the nearest 10. Work out the upper and lower bounds of the number.
Upper bound 650 , lower bound 550

Upper bound 605 , lower bound 595

Upper bound 604 , lower bound 595

Upper bound 649 , lower bound 550

The place value here is 10.
10 \div 2 = 5 600+5=605, \; 600-5=595
3. A number is given as 56.28 to 2 decimal places. Write down the error interval for the number.




The place value here is 0.01.
0.01\div 2 = 0.005 56.28+0.005=56.285, \; 56.28-0.005=56.275
56.275 \leq x < 56.285
4. A number is given as 70 to 1 significant figure. Calculate the upper and lower bounds of the number.
Upper bound 74.99 , lower bound 65

Upper bound 74 , lower bound 66

Upper bound 75 , lower bound 65

Upper bound 74 , lower bound 65

The place value here is 10.
10 \div 2 =5 70+5=75, \; 70-5=65
5. A number is given as 3.9 correct to 2 significant figures. Find the error interval for the number.




The place value here is 0.1.
0.1 \div 2=0.05 3.9+0.05=3.95, \; 3.9-0.05=3.85
3.85 \leq x < 3.95
6. A number is given as 0.0456 correct to 3 significant figures. Calculate the upper and lower bounds of the number.
Upper bound 0.0455 , lower bound 0.0445

Upper bound 0.04565 , lower bound 0.04555

Upper bound 0.04564 , lower bound 0.04555

Upper bound 0.046 , lower bound 0.045

The place value here is 0.0001.
0.0001 \div 2 = 0.00005 0.0456+0.00005=0.04565, \; 0.0456-0.00005=0.04555
How to calculate upper and lower bounds GCSE questions
1. The length of a line is given as 18cm to the nearest cm. Find the upper and lower bounds of the length of the line.
(2 marks)
Upper bound: 18+0.5=18.5cm
(1)
Lower bound: 18-0.5=17.5cm
(1)
2. (a) The weight of a car is 850kg to the nearest kg. Work out the upper bound of the weight of the car.
(b) The length of the car is 4.25m to the nearest centimetre. Work out the error interval for the length of the car.
(5 marks)
(a)
1 \div 2 =0.5
(1)
850+0.5=850.5kg
(1)
(b)
Upper bound: 4.25+0.005=4.255m or 425+0.5=425.5cm
(1)
Lower bound: 4.25-0.005=4.245m or 425-0.5=424.5cm
(1)
Error interval: 4.245 \leq x < 4.255\mathrm{m}~ or ~ 424.5 \leq x < 425.5 \mathrm{cm}
(1)
3. The diameter of a planet is 12000km to the nearest 1000km. Work out the upper bound and lower bound for the diameter of the planet.
(2 marks)
Upper bound: 12000+500=12500km
(1)
Lower bound: 12000-500=11500km
(1)
Learning checklist
You have now learned how to:
-
Calculate the upper and lower bounds of a rounded number
-
Write an error interval
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.