GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Addition and subtraction

Negative numbers Vector notation Column vectors Vector addition

This topic is relevant for:

GCSE Maths Geometry and Measure Vectors

Vector subtraction

Vector Subtraction

Here we will learn about vector subtraction.

There are also vector worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is vector subtraction?

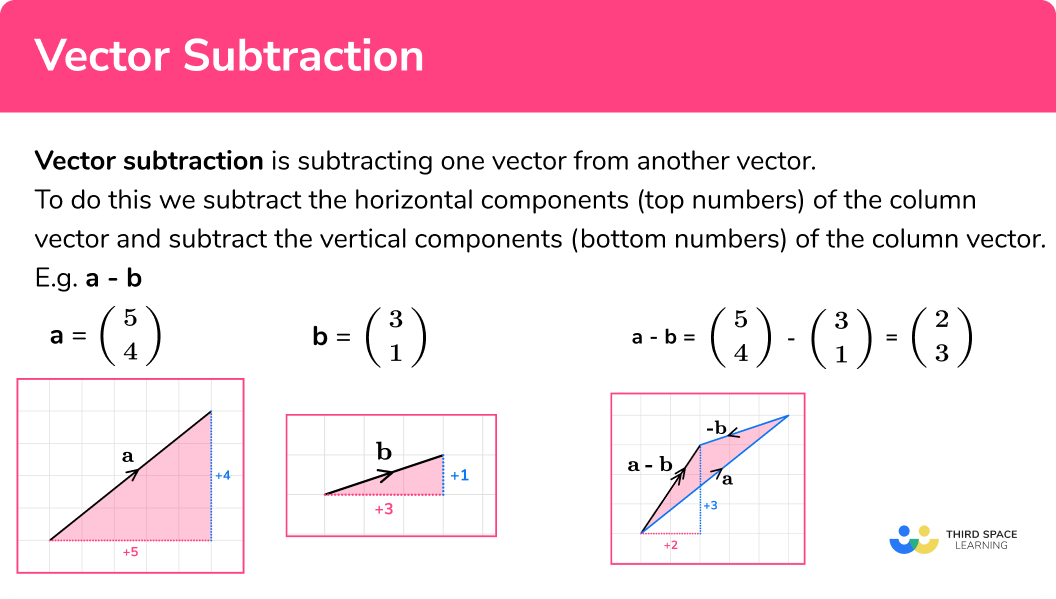
Vector subtraction is subtracting one vector from another vector.

To do this we subtract the horizontal components (top numbers) of the column vector and subtract the vertical components (bottom numbers) of the column vector.

E.g.

Let’s look at vector a and vector b.

\[\textbf{a}= \left(\begin{array}{1} 5\\ 4\\ \end{array}\right) \quad \textbf{b}= \left(\begin{array}{1} 3\\ 1\\ \end{array}\right)\]

\[\textbf{a}-\textbf{b}= \left(\begin{array}{1} 5\\ 4\\ \end{array}\right) – \left(\begin{array}{1} 3\\ 1\\ \end{array}\right) = \left(\begin{array}{1} 2\\ 3\\ \end{array}\right)\]

Subtracting vectors is based on the addition of vectors. The first vector stays the same, but the second vector reverses to the opposite direction to become a negative vector.

\mathbf{a}-\mathbf{b}=\mathbf{a}+-\mathbf{b}

Using vector a and vector b let’s see what happens.

\[\textbf{a}= \left(\begin{array}{1} 5\\ 4\\ \end{array}\right)\]

\[\textbf{b}= \left(\begin{array}{1} 3\\ 1\\ \end{array}\right)\]

We need the vector –b. The direction of the vector –b is opposite to the direction of the original vector b (but has the same magnitude).

\[-\textbf{b}= \left(\begin{array}{1} -3\\ -1\\ \end{array}\right)\]

So,

\textbf{a} - \textbf{b}= \textbf{a}+ - \textbf{b}

We know from vector addition that when adding two vectors, we add the second onto the end of the first, as shown here:

The final answer is known as the resultant vector.

\[\textbf{a}-\textbf{b}=\textbf{a}+ -\textbf{b}= \left(\begin{array}{1} 5\\ 4\\ \end{array}\right) +\ \left(\begin{array}{1} -3\\ -1\\ \end{array}\right) = \left(\begin{array}{1} 2\\ 3\\ \end{array}\right)\]

Therefore

\[\textbf{a} – \textbf{b}= \left(\begin{array}{1} 5\\ 4\\ \end{array}\right) -\ \left(\begin{array}{1} 3\\ 1\\ \end{array}\right) = \left(\begin{array}{1} 2\\ 3\\ \end{array}\right)\]

What is vector subtraction?

How to subtract vectors

In order to subtract a vector from an original vector:

Subtract the $x$ components.
Subtract the $y$ components.
Write the resultant vector.

How to subtract vectors

Vectors worksheet (includes vector subtraction)

Get your free vector subtraction worksheet of 20+ vectors questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Vectors worksheet (includes vector subtraction)

Get your free vector subtraction worksheet of 20+ vectors questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on vectors

Vector subtraction is part of our series of lessons to support revision on vectors. You may find it helpful to start with the main vectors lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Vector subtraction examples

Example 1: subtract vectors

Work out:

\[\left(\begin{array}{1} 6\\ 4\\ \end{array}\right) -\ \left(\begin{array}{1} 4\\ 3\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

6-4=2

2Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

4-3=1

3Write the resultant vector.

\[\left(\begin{array}{1} 6\\ 4\\ \end{array}\right) -\ \left(\begin{array}{1} 4\\ 3\\ \end{array}\right) = \left(\begin{array}{1} 2\\ 1\\ \end{array}\right)\]

Example 2: subtract vectors

Work out:

\[\left(\begin{array}{1} 3\\ 2\\ \end{array}\right) -\ \left(\begin{array}{1} 5\\ 1\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

3-5=-2

Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

2-1=1

Write the resultant vector.

Write the two answers as a column vector

\[\left(\begin{array}{1} 3\\ 2\\ \end{array}\right) -\ \left(\begin{array}{1} 5\\ 1\\ \end{array}\right) = \left(\begin{array}{1} -2\\ 1\\ \end{array}\right)\]

Example 3: subtract vectors

Work out:

\[\left(\begin{array}{1} 2\\ 4\\ \end{array}\right) -\ \left(\begin{array}{1} 2\\ 6\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

2-2=0

Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

4-6=-2

Write the resultant vector.

Write the two answers as a column vector

\[\left(\begin{array}{1} 2\\ 4\\ \end{array}\right) -\ \left(\begin{array}{1} 2\\ 6\\ \end{array}\right) = \left(\begin{array}{1} 0\\ -2\\ \end{array}\right)\]

Example 4: subtract vectors

Work out:

\[\left(\begin{array}{1} -4\\ 3\\ \end{array}\right) -\ \left(\begin{array}{1} 2\\ 1\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

-4-2=-6

Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

3-1=2

Write the resultant vector.

Write the two answers as a column vector

\[\left(\begin{array}{1} -4\\ 3\\ \end{array}\right) -\ \left(\begin{array}{1} 2\\ 1\\ \end{array}\right) = \left(\begin{array}{1} -6\\ 2\\ \end{array}\right)\]

Example 5: subtract vectors

Work out:

\[\left(\begin{array}{1} -5\\ 2\\ \end{array}\right) -\ \left(\begin{array}{1} -3\\ -2\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

-5-(-3)=-2

Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

2-(-2)=4

Write the resultant vector.

Write the two answers as a column vector

\[\left(\begin{array}{1} -5\\ 2\\ \end{array}\right) -\ \left(\begin{array}{1} -3\\ -2\\ \end{array}\right) = \left(\begin{array}{1} -2\\ 4\\ \end{array}\right)\]

Example 6: subtract vectors

Work out:

\[\left(\begin{array}{1} 2\\ -1\\ \end{array}\right) -\ \left(\begin{array}{1} -4\\ -3\\ \end{array}\right)\]

Subtract the $x$ components.

Subtract the second top number from the first top number

2-(-4)=6

Subtract the $y$ components.

Subtract the second bottom number from the first bottom number

-1-(-3)=2

Write the resultant vector.

Write the two answers as a column vector

\[\left(\begin{array}{1} 2\\ -1\\ \end{array}\right) -\ \left(\begin{array}{1} -4\\ -3\\ \end{array}\right) = \left(\begin{array}{1} 6\\ 2\\ \end{array}\right)\]

Common misconceptions

Subtracting negative integers

Mistakes can easily be made when subtracting negative integers.

Make sure that negative numbers skills are well practiced.

E.g.

3-(-4)=3+4=7

Order of the subtraction

The order in which subtraction occurs is very important. Vector subtraction is NOT commutative and must be carried out in the stated order.
etc.

a - b \neq b - a

Column vectors notation

Column vectors only have $2$ numbers within the brackets, they have the top number and the bottom number.

There is no need for any other punctuation marks such as commas or semicolons and there is no need for a line to separate the numbers.

A final answer of $0$

The $x$ component or the $y$ component can be $0$ . If both vector components are $0$ then the final resultant vector would be the vector $0$ . This is known as the null vector or the zero vector.

E.g.

\[\left(\begin{array}{1} 3\\ 7\\ \end{array}\right) -\ \left(\begin{array}{1} 3\\ 7\\ \end{array}\right) = \left(\begin{array}{1} 0\\ 0\\ \end{array}\right)\]

Practice vector subtraction questions

\begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; -2 \; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; -2 \; \end{pmatrix}

\textbf{v}-\textbf{w}= \begin{pmatrix} \; 7 \;\\ \; 3 \; \end{pmatrix} – \begin{pmatrix} \; 4 \;\\ \; 1 \; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; 5 \; \end{pmatrix}

\begin{pmatrix} \; -3 \;\\ \; -5 \; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}

\begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix}

\textbf{c}-\textbf{d}= \begin{pmatrix} \; 6 \;\\ \; 2 \; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 7 \; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; -6 \;\\ \; -2 \; \end{pmatrix}

\begin{pmatrix} \; -6 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; -2 \; \end{pmatrix}

\textbf{b}-\textbf{a}= \begin{pmatrix} \; 5 \;\\ \; 4 \; \end{pmatrix} – \begin{pmatrix} \; -1 \;\\ \; 6 \; \end{pmatrix} = \begin{pmatrix} \; 6 \;\\ \; -2 \; \end{pmatrix}

\begin{pmatrix} \; -1 \;\\ \; -2 \; \end{pmatrix}

\begin{pmatrix} \; -1 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; 1 \;\\ \; -2 \; \end{pmatrix}

\begin{pmatrix} \; 1 \;\\ \; 2 \; \end{pmatrix}

\textbf{p}-\textbf{q}= \begin{pmatrix} \; -3 \;\\ \; 6 \; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\ \; 4 \; \end{pmatrix} = \begin{pmatrix} \; -1 \;\\ \; 2 \; \end{pmatrix}

\begin{pmatrix} \; -5 \;\\ \; 6 \; \end{pmatrix}

\begin{pmatrix} \; -5 \;\\ \; -6 \; \end{pmatrix}

\begin{pmatrix} \; 5 \;\\ \; 6 \; \end{pmatrix}

\begin{pmatrix} \; 5 \;\\ \; -6 \; \end{pmatrix}

\textbf{s}-\textbf{r}= \begin{pmatrix} \; -2 \;\\ \; -1 \; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; -5 \;\\ \; -6 \; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; -3 \; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\ \; -3 \; \end{pmatrix}

\textbf{e}-\textbf{d}= \begin{pmatrix} \; -4 \;\\ \; 3 \; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\ \; 6 \; \end{pmatrix} = \begin{pmatrix} \; -2 \;\\ \; -3 \; \end{pmatrix}

Vector subtraction GCSE questions

1. Vector $\textbf{v}$ is $\begin{pmatrix} \; 3 \;\\ \; 1 \; \end{pmatrix}$

Vector $\textbf{w}$ is $\begin{pmatrix} \; 2 \;\\ \; 4 \; \end{pmatrix}$

Which of the following vectors is the answer to $\textbf{w}-\textbf{v}$ ?

A	$\quad \quad$	B	$\quad \quad$	C	$\quad \quad$	D
$\begin{pmatrix} \; -1 \;\\ \; 3 \; \end{pmatrix}$	$\quad \quad$	$\begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pmatrix}$	$\quad \quad$	$\begin{pmatrix} \; 1 \;\\ \; -3 \; \end{pmatrix}$	$\quad \quad$	$\begin{pmatrix} \; -1 \;\\ \; -3 \; \end{pmatrix}$

(1 mark)

Show answer

(1)

2. Here are two vectors.

$\textbf{m}= \begin{pmatrix} \; 2 \;\\ \; -4 \; \end{pmatrix} \;$ and $\; \textbf{n}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pmatrix}$

Work out $\; \textbf{n}-\textbf{m}$

(2 marks)

Show answer

\textbf{n}-\textbf{m}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pmatrix} – \begin{pmatrix} \; 2 \;\\ \; -4 \; \end{pmatrix} = \begin{pmatrix} \; 1 \;\\ \; -2 \; \end{pmatrix}

For the $x$ component (top number)

(1)

For the $y$ component (bottom number)

(1)

3. Here is a vector subtraction

\begin{pmatrix} \; \text{a} \;\\ \; -1 \; \end{pmatrix} – \begin{pmatrix} \; 2 \;\\ \; \text{b} \; \end{pmatrix} = \begin{pmatrix} \; 4 \;\\ \; 2 \; \end{pmatrix}

(a) Find the value of $a$ .

(b) Find the value of $b$ .

(2 marks)

Show answer

(a)

a=6

(1)

(b)

b=-3

(1)

Learning checklist

You have now learned how to:

Subtract vectors

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What is vector subtraction?

How to subtract vectors

Vector subtraction worksheets

Vector subtraction examples

↓

Example 1: subtract vectors Example 2: subtract vectors Example 3: subtract vectors Example 4: subtract vectors Example 5: subtract vectors Example 6: subtract vectors

Common misconceptions

Practice vector subtraction questions

Vector subtraction GCSE questions

Learning checklist

Next lessons

Still stuck?