GCSE Maths Mark Schemes: A Toolkit for Heads of Department

GCSE maths mark schemes reveal exactly how examiners award marks across all three papers. Without understanding how Edexcel examiners award marks across Paper 1 (non-calculator), Paper 2, and Paper 3 (both calculator papers), students lose marks on questions they could answer, simply because their working doesn’t match what examiners expect.

Understanding Edexcel mark schemes helps you identify exactly where your students lose marks and how to teach them to recover those marks. The mark scheme codes, from M1 (method marks) to A1 (accuracy marks), show precisely what examiners look for when awarding credit across foundation and higher tier GCSE maths papers.

This guide shows you how to interpret the GCSE maths mark scheme, use it alongside Edexcel past papers to improve student outcomes, and ensure your marking of mock exam papers aligns with examiner expectations.

Key takeaways

• GCSE maths mark schemes show exactly how examiners award marks across calculator and non-calculator papers for both foundation and higher tiers
• Understanding mark scheme notation helps teachers identify common misconceptions and teach exam technique alongside mathematical content
• The majority of marks in GCSE Maths are awarded for method/process, not just the final answer.
• Past papers from Edexcel, AQA, and OCR provide authentic exam practice, while mark schemes reveal what examiners expect in student working
• Video solutions and worked examples complement mark schemes by showing the full solution process
• Regular practice with exam papers and mark schemes helps students improve accuracy and feel confident on exam day

What is a GCSE maths mark scheme?

A GCSE maths mark scheme is the official document showing exactly how examiners award marks for each question on exam papers. Each exam board publishes their own mark schemes, including Edexcel, AQA, OCR, and WJEC, covering all three papers for both Higher and Foundation tiers.

Each mark scheme includes details on:

• Method marks (M1, M2) showing credit for correct mathematical processes
• Accuracy marks (A1, A2) awarded for correct final answers
• Alternative methods and acceptable answers marked as ‘oe’ (or equivalent)
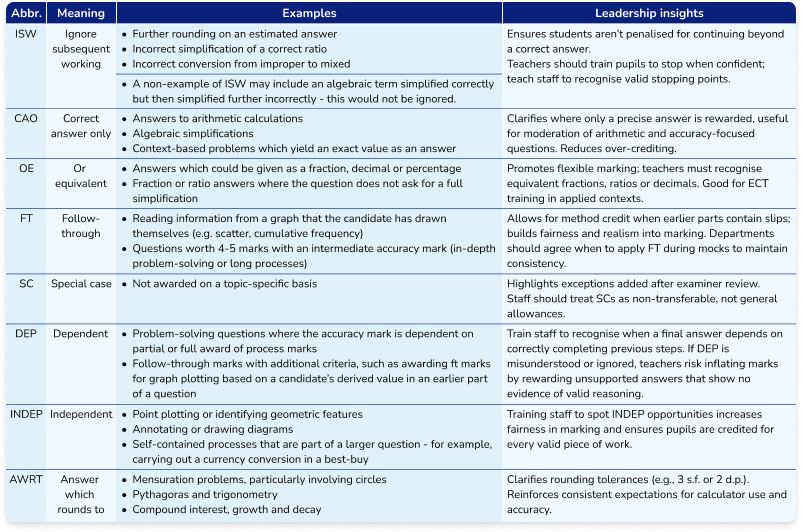
• Special marking codes like ISW (ignore subsequent working) and FT (follow through)

The mark scheme reveals what examiners expect to see in student working, which is crucial for maximising scores, particularly important when the difference between grades can be just a few marks.

GCSE MATHS 2026: STAY UP TO DATE

Join our email list to stay up to date with the latest news, revision lists and resources for GCSE maths 2026. We’re analysing each paper during the course of the 2026 GCSEs in order to identify the key topic areas to focus on for your revision.

GCSE dates 2026
GCSE results (2026 when available)

Get ahead on revision with the GCSE maths papers analysis from 2025:
Analysis of GCSE Maths Paper 1 2025
Analysis of GCSE Maths Paper 2 2025
GCSE Maths Paper Analysis and Summary 2025
GCSE Maths Teacher Survey Results 2025

Understanding mark scheme notation and codes

Mathematics mark schemes use specific codes to show how examiners award marks. A shared understanding of these codes across maths departments creates consistency in marking and learner preparation for the June and November exams.

Common Edexcel mark scheme codes:

Code	Meaning	Examiner/Teaching Focus
M	Method mark	Credit for correct process, even with arithmetic slip.
A	Accuracy mark	Awarded for a correct answer; usually dependent on a preceding M mark.
B	Independent mark	Unconditional Accuracy Marks (B) are awarded for specific points that are independent of method marks.
ISW	Ignore subsequent working	Do not penalise if a correct answer is followed by incorrect simplification or further work.
CAO	Correct answer only	No partial method marks available.
OE	Or equivalent	Alternative forms (fraction, decimal, percentage) or valid alternative methods are accepted.
FT	Follow-through	Credit for correct method applied to an earlier, incorrect result.
DEP	Dependent	Mark is only awarded if a specific previous mark (M or P) has been awarded.
AWRT	Answer which rounds to	Allows for specified rounding tolerances (e.g., 3 s.f. or 2 d.p.).
SC	Special Case	Marks awarded for a common misinterpretation or partial answer of mathematical worth, as explicitly listed in the scheme.

The notation can feel complex at first. Our Edexcel mark scheme decoder breaks down these codes into plain language, helping you quickly identify what students need to demonstrate for each mark.

Where to find GCSE maths past papers and mark schemes

Accessing official Edexcel past papers and mark schemes is key to effective revision and accurate mock exam marking.

Edexcel GCSE maths past papers and mark schemes

The Pearson Edexcel website hosts all past papers and mark schemes from recent exam series. You can select the exam series (June or November) and tier (foundation or higher) to download Paper 1, Paper 2, or Paper 3.

Mark schemes are published shortly after each exam series. Older papers from previous years remain available, providing extensive practice material.

Video solutions for many Edexcel papers are available through educational platforms and YouTube channels. These walkthroughs complement mark schemes by showing the complete working process, helping you demonstrate exam technique to students.

Other exam boards

• AQA GCSE maths papers and mark schemes follow similar conventions
• OCR GCSE maths papers offer alternative question styles
• WJEC GCSE maths papers are aligned with the Welsh curriculum

How GCSE maths paper structure affects departmental marking strategy

Understanding how Edexcel structures its three exam papers helps you apply mark schemes more strategically across your department and when analysing mock results.

Each GCSE maths paper is worth 80 marks (240 marks total) and tests different Assessment Objectives (AOs), which influences mark scheme application:

Paper 1 (non-calculator) mark schemes reward method over accuracy

With no calculator access across the 1 hour 30 minute paper, Paper 1 heavily tests AO1 (use and apply standard techniques), leading to generous method marks (M1, M2) even when arithmetic slips occur. This makes Paper 1 a strategic focus for intervention—students can recover marks through clear working even when calculations go wrong.

When training teachers to mark Paper 1 mocks, emphasise that examiners expect to see full working and award method marks generously, particularly on algebra, ratio, and geometry questions.

Calculator papers demand higher accuracy standards

Paper 2 and Paper 3 (both calculator papers, 1 hour 30 minutes each) incorporate more AO2 (reasoning, interpreting, and communicating mathematically)and AO3 (solving problems), which often carry higher marks and require structured working. Mark schemes for calculator papers reflect examiner expectations that calculator access should eliminate basic arithmetic errors.

Both calculator papers expect:

• Precise decimal and percentage calculations
• Correct rounding to specified significant figures
• Complete, coherent multi-step solutions for full credit

When moderating calculator paper marking across your department, focus on whether teachers are applying the stricter accuracy standards (A1, A2) that examiners use, particularly on questions marked CAO (correct answer only) or AWRT (answer which rounds to).

Foundation vs Higher tier mark scheme expectations

• Foundation tier exam papers (grades 1–5) reward partial method marks generously, making them more forgiving of incomplete working.
• Higher tier exam papers (grades 4–9) require complete, structured solutions—students who skip steps lose marks even if their final answer is correct.

This distinction matters when training teachers to mark mixed-ability groups or when deciding which tier suits borderline students. The 240 marks across all three exam papers convert to final grades using grade boundaries that vary each exam series—understanding tier-specific mark scheme conventions helps you predict outcomes more accurately.

For a detailed analysis of how raw marks convert to grades, see our article on GCSE grade boundaries.

Training your department to use mark schemes consistently

Aligned marking standards across your department ensure fair assessment, reliable grade predictions, and comparable data between classes. When every teacher interprets mark schemes the same way, students receive consistent feedback, and your intervention targeting becomes more accurate.

Why consistency matters

Even experienced teachers can apply mark schemes differently. Some under-credit method marks, others over-credit final answers, and interpretations of follow-through (FT) and dependent (DEP) marks vary significantly. These inconsistencies impact:

• Grade predictions: Variations in marking can shift predicted grades by a full boundary
• Student confidence: Inconsistent feedback confuses students about examiner expectations
• Data reliability: Comparing results across classes becomes meaningless when marking standards differ

Running effective moderation sessions

Schedule short, focused calibration sessions three to four times per year – ideally after mock exams. Each session should take 15–20 minutes during a department meeting.

Suggested structure:

1. Select: Choose one or two multi-mark questions from a recent mock or past paper
2. Live-mark: Teachers individually mark 3–5 anonymised student responses using mark scheme codes
3. Compare: Review outcomes together, debate borderline decisions, and agree on criteria
4. Record: Document agreed marking standards, particularly for borderline responses

Include deliberate borderline cases where the marking judgement varies. Focus on questions where your department consistently disagrees – these reveal where clarity is most needed.

Apply mark schemes as examiners would

Use the exact marking codes and conventions from official mark schemes:

• Award method marks (M1, M2) for correct processes, regardless of final accuracy
• Only give accuracy marks (A1, A2) when answers match the mark scheme exactly (or are marked ‘oe’ for equivalent forms)
• Apply CAO (correct answer only) strictly; these questions offer no partial credit
• Recognise follow-through (FT) marks where students apply the correct method to an earlier error

Common examiner pitfalls

Train your team to spot:

• Premature approximation: Rounding off too early should be penalised by 1 mark if it leads to an inaccurate final answer
• Contradictory working:If a student shows two different methods/answers, mark only the one that gives the least marks
• Misread/miscopy: A genuine error in copying a number from the question means the student only loses the accuracy marks (A/B), not the method marks (M)

Building a shared marking framework

Create a departmental marking handbook that includes:

• Agreed interpretations of common mark scheme codes
• Examples of borderline responses with agreed marks
• Topic-specific guidance (for instance, how your department handles ratio simplification or angle reasoning)
• Notes from moderation sessions

Store exemplar scripts for new staff induction. When ECTs, non-specialists, or teachers new to Edexcel join your department, this framework helps them align with established standards quickly.

Supporting non-examiner teachers

Teachers without formal examination experience benefit most from structured support. The Edexcel mark scheme decoder translates examiner codes into plain language, helping all teachers – regardless of experience – apply mark schemes accurately.

Pair less experienced markers with qualified examiners during mock marking periods. This mentoring approach builds confidence and ensures consistency without requiring formal examiner training for every teacher.

Measuring impact

Track marking consistency through:

• Comparing predicted grades to final results each year
• Monitoring variation in mock results between classes
• Reviewing moderation session outcomes to see if disagreements decrease over time

When your department applies mark schemes with shared understanding, internal assessments become predictive, reliable, and comparable, making your data genuinely useful for targeting intervention and tracking progress.

How to use mark schemes effectively with your students

Mark schemes pinpoint exactly where examiners award credit and where they don’t. This insight helps you teach students the difference between knowing mathematics and demonstrating that knowledge under exam conditions.

When students understand that showing clear working, using correct notation, and structuring multi-step solutions properly can be worth more than half the marks on a paper, their approach to revision and exam preparation switches from answer-focused to method-focused.

Model exam technique using mark schemes

Show learners examples from past GCSE maths papers where:

• Partial credit is awarded for the method despite incorrect final answers
• Missing working leads to zero marks on multi-mark questions
• Ambiguous notation loses the accuracy marks

Walk through worked solutions that mirror mark scheme expectations, demonstrating the complete solution process and how experienced mathematicians approach exam questions.

Identify common marking pitfalls

Use mark scheme analysis to identify common errors, such as:

• Insufficient working: Multi-mark questions require visible method steps
• Accuracy requirements: Calculator paper mark schemes expect precision in decimal places and significant figures
• Contradictory working: If students show two methods reaching different answers, mark schemes typically award no accuracy, even if one method is correct

Use this information to design targeted teaching interventions, develop student checklists for self-assessment, and inform mock exam feedback with precise, actionable guidance.

Mark mock exams accurately

Consistent mock marking gives students realistic grade predictions and ensures your intervention targets the right areas. Train your department to:

• Award credit for valid approaches even when final answers are incorrect
• Recognise when follow-through (FT) applies after earlier errors
• Identify independent (INDEP) marks that can be awarded regardless of previous work

Download the Edexcel mark scheme decoder to simplify this process and translate examiner codes into clear guidance for marking practice papers.

Addressing knowledge gaps identified through mark schemes

Mark schemes don’t just identify where marks were lost, they diagnose why students struggled and which gaps need addressing. This diagnostic insight helps you target intervention time where it will have the greatest impact on exam outcomes.

Analyse patterns across your cohort

After marking mocks using mark schemes, look for consistent patterns:

• Which topics consistently lose marks? If most students lose method marks on ratio questions or accuracy marks on circle theorems, these topics need priority attention
• Are errors due to content gaps or exam technique? Students might understand fractions but lose marks through poor notation, or know Pythagoras but fail to show sufficient working for method marks

Mark schemes make this distinction clear. Content gaps require reteaching; exam technique issues need targeted practice with mark scheme feedback.

Design targeted intervention

Use mark scheme analysis to create a focused intervention:

• Identify specific misconceptions from mark schemes rather than broad topic weaknesses
• Teach to the mark scheme by showing students what examiners credit and what they don’t
• Provide practice on high-value question types where small improvements yield multiple marks

For example, if mark schemes show students lose marks on “show that” questions through incomplete working, create practice specifically addressing this question type with clear mark scheme guidance.

Track progress through subsequent papers

Use mark schemes from past papers to measure whether the intervention has closed gaps:

• Compare performance on similar question types across different exam series
• Track the method mark recovery as students improve their working
• Adjust teaching focus based on which gaps remain stubborn

When mark schemes reveal persistent gaps in topics like fractions, algebra, or geometry, Third Space Learning’s AI tutor Skye provides one-to-one maths support. Skye delivers personalised lessons aligned with GCSE exam boards, helping Year 10 and Year 11 students master challenging content before exam papers.

Build mark scheme fluency across your department

When your department applies GCSE maths mark schemes consistently, you move from guessing where students struggle to knowing exactly which question types lose marks and why. This precision helps you target interventions, train new teachers, and prepare students for exam papers.

The three actions that make the biggest difference:

1. Run short moderation sessions to align marking standards
2. Analyse mock results through mark scheme data to identify gaps
3. Ensure every teacher, including ECTs and non-specialists, can interpret examiner codes accurately

Start with one focused moderation session using a recent past paper. Compare how your team awards method marks versus accuracy marks, document your agreed standards, then apply those standards consistently across all mock marking. When students receive feedback aligned with actual examiner expectations, they know exactly what to improve before exam day.

GCSE maths mark schemes FAQs