High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Fractions Decimals Mixed number to improper fraction Numerator and denominatorFraction to decimal
Here you will learn about converting fractions to decimals using division and using a calculator.
Students will first learn about converting fractions to decimals as part of number and operations fractions in 4th grade. They expand their knowledge of converting fractions to decimals as part of the number system in 7th grade.
What is converting fractions to decimals?
Converting fractions to decimals is representing a fraction as a decimal without changing its value.
For example,
\cfrac{1}{4}=0.25
\cfrac{1}{8}=0.125
\cfrac{2}{7}=0.2857142857…
3 \cfrac{1}{5}=3.2
What is converting fractions to decimals?

Fraction to Decimal Worksheet

We’ve got your class prep covered with this worksheet to help bring more fraction to decimal practice into the classroom. Includes 15 questions written by teachers like you, plus answer key and related standard.
DOWNLOAD FREE
Fraction to Decimal Worksheet

We’ve got your class prep covered with this worksheet to help bring more fraction to decimal practice into the classroom. Includes 15 questions written by teachers like you, plus answer key and related standard.
DOWNLOAD FREECommon Core State Standards
How does this relate to 7th grade math?
- 7th grade – The Number System (7.NS.2d)
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0 s or eventually repeats.
How to convert fractions to decimals
In order to convert from a fraction to a decimal:
- Ensure the fraction is written with just a numerator and a denominator. If needed convert the mixed number to an improper fraction.
- Divide the numerator by the denominator.
- State the answer clearly in the form ‘fraction’=’decimal.’
Converting fractions to decimals examples
Example 1: converting a simple fraction to a decimal
Convert \cfrac{1}{2} to a decimal.
- If needed convert the mixed number to an improper fraction.
There is no need to convert as the fraction is already in the correct form.
2Divide the numerator by the denominator.
1 \div 2 \quad You can use long division here.
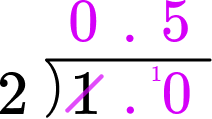
3State the answer clearly in the form ‘fraction’=’decimal.’
\cfrac{1}{2} = 0.5
Example 2: converting a fraction to a decimal
Convert \cfrac{3}{8} \, to a decimal.
If needed convert the mixed number to an improper fraction.
There is no need to convert as the fraction is already in the correct form.
Divide the numerator by the denominator.
3 \div 8
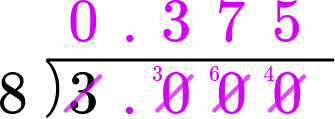
State the answer clearly in the form ‘fraction’=’decimal.’
\cfrac{3}{8}=0.375
Example 3: converting an improper fraction to a decimal
Convert \cfrac{7}{5} \, to a decimal.
If needed convert the mixed number to an improper fraction.
There is no need to convert as the fraction is already an improper fraction.
Divide the numerator by the denominator.
7 \div 5
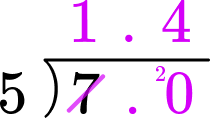
State the answer clearly in the form ‘fraction’=’decimal.’
\cfrac{7}{5}=1.4
Example 4: converting a mixed number to a decimal
Convert 3 \cfrac{1}{4} \, to a decimal.
If needed convert the mixed number to an improper fraction.
You need to convert this mixed number to an improper fraction.
3 \cfrac{1}{4}= \cfrac{13}{4}
Divide the numerator by the denominator.
13\div{4}
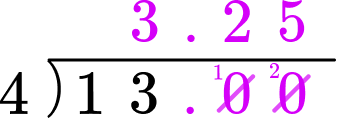
State the answer clearly in the form ‘fraction’=’decimal.’
3 \cfrac{1}{4}=3.25
Example 5: converting a fraction to a decimal involving a repeating decimal
Convert \cfrac{2}{9} \, to a decimal.
If needed convert the mixed number to an improper fraction.
There is no need to convert as the fraction is already in the correct form.
Divide the numerator by the denominator.
2 \div 9
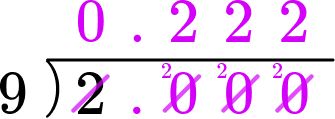
You will notice here that the 2 is repeated and will continue to be repeated. This is therefore a recurring, or repeating decimal and can be shown in the form.
0.\overline{2}
State the answer clearly in the form ‘fraction’=’decimal.’
\cfrac{2}{9}=0 . \overline{2}
Example 6: converting a mixed number to a decimal involving a repeating decimal
Convert 2\cfrac{1}{7} \, to a decimal.
If needed convert the mixed number to an improper fraction.
You need to convert this mixed number to an improper fraction.
2\cfrac{1}{7}=\cfrac{15}{7}
Divide the numerator by the denominator.
15 \div 7 \quad You can use long division here.
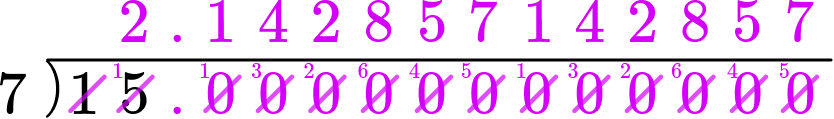
You will notice here that the numbers 1 \, 4 \, 2 \, 8 \, 5 \, 7 after the decimal place are repeated and will continue to be repeated.
This is therefore a repeating decimal and can be shown in the form 0.\overline{142857}, so the whole decimal can be shown as 2.\overline{142857}
State the answer clearly in the form ‘fraction’=’decimal.’
2\cfrac{1}{7}=2 . \overline{142857}
Calculator skills
You can perform a fraction to decimal conversion on a calculator by dividing the numerator by the denominator as a simple division equation. Another way is by inputting the fraction into your calculator and then pressing the [s ⇔ d] button.
For example, convert \cfrac{5}{4} to a decimal.
Press the fraction button on the left side of your calculator.

Input the numbers and press the = button.

Press the [ s ⇔ d ] button to have it shown as a decimal.
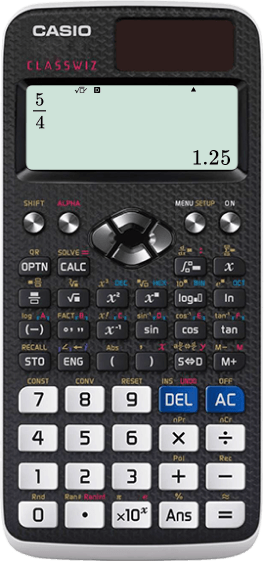
Therefore, \cfrac{5}{4}=1.25
See also: Calculator skills
Teaching tips for fractions to decimals
- Students will need to have a strong foundation in division and specifically the standard algorithm of division, or long division. Students should also understand the terms dividend and divisor. Review if needed before starting this topic.
- Begin with fractions that convert to simple decimal numbers ending in the tenths, hundredths, or thousandths place. Then move on to fractions that convert to more complex terminating decimals before moving onto fractions that convert to repeating decimals.
- Once students have mastered the calculations, move on to higher-level worksheets that provide them with word problems to provide a real-world context to the topic, which will deepen their understanding. For example, give students a division problem that requires them to use fraction to decimal conversion to calculate a percentage.
Easy mistakes to make
- Incorrectly converting between a mixed number and an improper fraction
Not correctly converting between numbers in different forms. For example, mixed numbers and improper fractions or forgetting to convert to an improper fraction and using the fractional part of a mixed number only.
- Making mistakes when dividing
Incorrectly using the standard algorithm of division (or long division).
- Flipping the division order
Incorrectly dividing the denominator (bottom number) by the numerator (top number), not the other way around.
For example, \cfrac{5}{7} \, means 5 \div 7 not 7 \div 5.
Related lessons on converting fractions, decimals, and percentages
Practice converting fractions to decimals questions
1. Convert \cfrac{1}{4} \, to a decimal.




2. Convert \cfrac{7}{8} \, to a decimal.




3. Convert \cfrac{7}{4} \, to a decimal.




4. Convert 7\cfrac{3}{5} \, to a decimal.




Converting to an improper fraction gives \cfrac{38}{5}, then 38\div5 = 7.6
5. Convert \cfrac{4}{9} \, to a decimal.




Dividing 4\div9 gives the repeating decimal 0. \overline{4}. The line above the 4 represents the 4 repeated infinitely.
6. Convert \cfrac{2}{11} \, to a decimal.




Dividing 2\div11 gives the repeating decimal 0. \overline{18}. The line above the 1 and 8 represents the 1 and 8 being repeated infinitely.
Fractions to decimals FAQs
Mixed fractions, also called mixed numbers, are numbers that contain a whole number and a proper fraction. For example, 2\frac{1}{2} is a mixed fraction.
To convert a fraction to a decimal, divide the numerator by the denominator. If the fraction is a mixed number, be sure to convert it to an improper fraction first.
Method 1: Divide the numerator by the denominator as a simple division equation or Method 2: Press the fraction button on the left side of your calculator, input the numbers and press the = button, then press the [s ⇔ d] button to have the fraction shown as its decimal equivalent.
The next lessons are
- Percent
- Compound measures
- Arithmetic
- Properties of equality
- Addition and subtraction
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!