What are possible [katex] \textbf{x} [/katex] and [katex] \textbf{y} [/katex] values in a proportional relationship?

Proportional relationships can be represented on the coordinate plane, which includes all real numbers. Depending on the context, the values on the [katex] x [/katex]-axis and [katex] y [/katex]-axis can be any subset of real numbers. For example, if the [katex] x [/katex]-axis represents the number of workers, the [katex] x [/katex] values include all whole numbers. Or, if the [katex] x [/katex]-axis represents the area of a circle, the [katex] x [/katex] values include any real number.

Directly Proportional - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Fractions Decimals Multiplying and dividing integers Coordinate plane

What is a proportion in math

Math resources Ratio and proportion

Proportion

Directly proportional

Here we will learn what it means to be directly proportional, including what direct proportion is and how to solve direct proportion problems. We will also look at solving word problems involving direct proportions.

Students will first learn about what it means to be directly proportional as part of ratios and proportions in $7$ th grade.

What does it mean to be directly proportional?

A direct proportion is a type of proportionality relationship. For direct proportion, as one value increases, so does the other value and conversely, as one value decreases, so does the other value.

Direct proportions are useful in numerous real life situations such as exchange rates, conversion between units, and fuel prices.

Direct proportion formula

The direct proportion formula allows us to express the relationship between two variables, using an equivalence relationship.

When $y$ is directly proportional to $x,$ the value of $y \div x$ is a constant value. This is known as the constant of proportionality and is represented by the variable $k.$

Given that $k=y \div x,$ you can rearrange this formula to make $y$ the subject, and show the standard format of the direct proportion formula:

$y=kx$

Step-by-step guide: Direct variation equation

Graphs representing a direct proportion between two variables

Proportional relationships can also be represented graphically.

If you sketched the straight line graph for the equation $y=kx,$ the line must go through the origin $(0,0)$ as when $x=0, \, y=k\times{0}=0,$ and the slope of the line is equal to the value of $k.$

See also: Linear equations

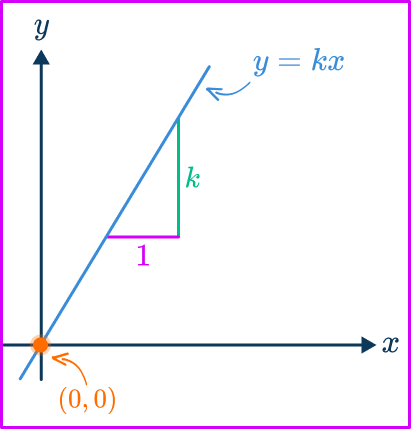
Note, the value of $y$ can be proportional to other powers of $x$ including $x^{2}, x^{3},$ or $\sqrt{x}.$ Each of these has a different algebraic and graphical representation, but they all share the same property of intersecting the origin.

What does it mean to be directly proportional?

Common Core State Standards

How does this relate to $7$ th grade math?

7.RP.A.2 (Ratios and Proportional Relationships)
Recognize and represent proportional relationships between quantities.
- Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
- Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.
- Represent proportional relationships by equations. For example, if total cost $t$ is proportional to the number $n$ of items purchased at a constant price $p,$ the relationship between the total cost and the number of items can be expressed as $t=pn.$
- Explain what a point $(x,y)$ on the graph of a proportional relationship means in terms of the situation, with special attention to the points $(0,0)$ and $(1,r)$ where $r$ is the unit rate.

[FREE] Ratio Worksheet (Grade 6 and 7)

Use this quiz to check your 6th and 7th grade students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Ratio Worksheet (Grade 6 and 7)

DOWNLOAD FREE

How to calculate directly proportional relationships

In order to calculate an unknown value given a directly proportional relationship:

Write down the direct proportion formula.
Determine the value of $\textbf{k}.$
Substitute $\textbf{k}$ and the known value into the direct proportion formula.
Solve the equation.

Direct proportion examples

Example 1: y is directly proportional to x (table)

Given that $y$ is directly proportional to $x,$ calculate the value for $y$ when $x=6.$

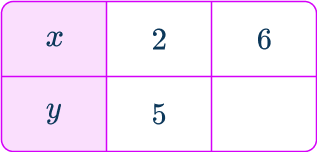
Write down the direct proportion formula.

Since $y$ is directly proportional to $x,$ you can use the formula $y=kx.$

2Determine the value of $\textbf{k}.$

From the table, you can see that when $x=2, \, y=5.$ By substituting these values into the formula, you get the value of $k.$

\begin{aligned}5&=k\times{2} \\\\ k&=5\div{2} \\\\ k&=2.5 \end{aligned}

3Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Substituting $k=2.5$ into the formula, you have:

y=2.5x

To find the value for $y$ when $x=6,$ substitute $x=6$ into the equation.

y=2.5\times{6}

4Solve the equation.

\begin{aligned}y&=2.5\times{6} \\\\ y&=15 \end{aligned}

Example 2: y is directly proportional to x (table)

$y$ is directly proportional to $x.$ Calculate the value for $x$ when $y=32.$

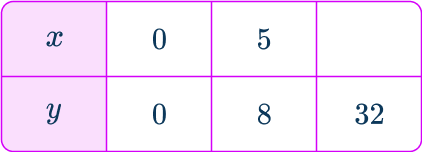
Write down the direct proportion formula.

Since $y$ is directly proportional to $x,$ you can use the formula $y=kx.$

Determine the value of $\textbf{k}.$

The constant of proportionality cannot be calculated at the point $(0,0)$ because by substituting this into the formula, you get $k=0\div{0}$ which is not mathematically possible as you cannot divide by $0.$

Therefore you have to use the other coordinate $(5,8)$ and substitute these values into $y=kx$ to calculate $k.$

When $x=5$ and $y=8,$

$\begin{aligned}8&=k\times{5} \\\\ k&=8\div{5} \\\\ k&=1.6 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Substituting $k=1.6$ into the formula, you have:

$y=1.6x$

To find the value for $x$ when $y=32,$ substitute $y=32$ into the equation.

$32=1.6 \times {x}$

Solve the equation.

\begin{aligned}32&=1.6\times{x} \\\\ 32&=x\times{1.6} \\\\ 32\div{1.6}&=x \\\\ x&=20 \end{aligned}

Example 3: y is directly proportional to x (table with fraction)

Given that $y$ is directly proportional to $x,$ calculate the value for $y$ when $x=5.$

Write down the direct proportion formula.

Since $y$ is directly proportional to $x,$ you can use the formula $y=kx.$

Determine the value of $\textbf{k}.$

From the table, you can see that when $x=\cfrac{1}{2}, \, y=3.$

By substituting these values into the formula, you get the value of $k.$

$\begin{aligned}3&=k\times\cfrac{1}{2} \\\\ k&=3\div\cfrac{1}{2} \\\\ k&=6\end{aligned}$

Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Substituting $k=6$ into the formula, you have:

$y=6x$

To find the value for $y$ when $x=5,$ substitute $x=5$ into the equation.

$y=6 \times {5}$

Solve the equation.

\begin{aligned}y&=6\times{5} \\\\ y&=30 \end{aligned}

Example 4: y is directly proportional to x (word problem)

A florist uses ribbon to trim bunches of flowers. $80 \, cm$ of ribbon is needed to make the trimmings on $2$ bunches of flowers. The florist has $9$ bunches of flowers to trim today. How much ribbon will be needed?

Write down the direct proportion formula.

Since each bunch of flowers requires a specific length of ribbon, the length of ribbon required $(r)$ is directly proportional to the number of bunches of flowers $(b).$

This means our direct proportion formula is $r=kb$ where $k$ represents the constant of proportionality.

Determine the value of $\textbf{k}.$

You know that $80 \, cm$ of ribbon is needed to trim $2$ bunches of flowers. This means that when $r=80, \, b=2.$ Substituting these values into the above formula, you have:

$\begin{aligned}80&=k\times{2} \\\\ 80\div{2}&=k \\\\ k&=40 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Now, $r=40b.$ You need to find out how much ribbon is needed for $9$ bunches of flowers, so substitute $b=9$ into the formula to get:

$r=40\times{9}$

Solve the equation.

\begin{aligned}r&=40\times{9} \\\\ r&=360 \,cm \end{aligned}

Example 5: y is directly proportional to x (word problem)

Tyler makes and sells bracelets. Tyler can make $3$ bracelets using $8$ feet of string. If Tyler has used $144$ feet of string this week, how many bracelets has Tyler made?

Write down the direct proportion formula.

Since each bracelet requires a specific length of string, the length of string required $(s)$ is directly proportional to the number of bracelets made $(b).$

This means our direct proportion formula is $b=ks$ where $k$ represents the constant of proportionality.

Determine the value of $\textbf{k}.$

You know that $8$ feet of string is needed for $3$ bracelets. This means that when $s=8, \, b=3.$ Substituting these values into the above formula, you have:

$\begin{aligned}3&=k\times{8} \\\\ 3\div{8}&=k \\\\ k&=\cfrac{3}{8}\end{aligned}$

Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Now, $b=\cfrac{3}{8}s.$

You need to find out how many bracelets were made with $144$ feet of string, so substitute $s=144$ into the formula to get:

$b=\cfrac{3}{8} \times 144$

Solve the equation.

\begin{aligned}b&=\cfrac{3}{8}\times{144} \\\\ b&=54\end{aligned}

Example 6: y is directly proportional to x (word problem)

Grayson read $56$ pages in $3$ hours and $16$ minutes. At this rate, how many minutes will it take Grayson to read $18$ pages?

Write down the direct proportion formula.

Since, on average, each pages takes a specific length of time to read, the minutes read $(r)$ is directly proportional to the number of pages read $(p).$

This means our direct proportion formula is $r=kp$ where $k$ represents the constant of proportionality.

Determine the value of $\textbf{k}.$

You know that $3$ hours and $16$ minutes is needed for $56$ pages.

Since $r$ represents minutes, you need to convert $3$ hours and $16$ minutes to minutes.

$3\times{60}=180$

$180+16=196 \text{ minutes}$

This means that when $r=196, \, p=56.$ Substituting these values into the above formula, you have:

$\begin{aligned}196&=k\times{56} \\\\ 196\div{56}&=k \\\\ k&=3.5 \end{aligned}$

Substitute $\textbf{k}$ and the known value into the direct proportion formula.

Now, $r=3.5p.$ You need to find out how many minutes are needed for $18$ pages, so substitute $p=18$ into the formula to get:

$r=3.5\times{18}$

Solve the equation.

\begin{aligned}r&=3.5\times{18} \\\\ r&=63\text{ minutes} \end{aligned}

Teaching tips for directly proportional

When students are first learning, provide worksheets and study materials that have real world examples of direct proportions for students to consider and compare to.

Make sure to expose students to many different forms of corresponding values. This means showing them directly proportional relationships in tables, graphs, equations and real world scenarios.

Easy mistakes to make

Adding the same thing to each side of a proportion
When solving a proportion using a table, the next value along for $x$ is $3$ more than the current value. The value for $y$ is calculated by adding $3$ to this value.

This does not preserve the constant ratio. This uses an additive relationship, rather than the required multiplicative relationship between two variables (the multiplier being the proportionality constant, $k$ ).

For example,
When given the following proportional relationship in a table, look at the relationship between $x$ and $y$ to solve correctly.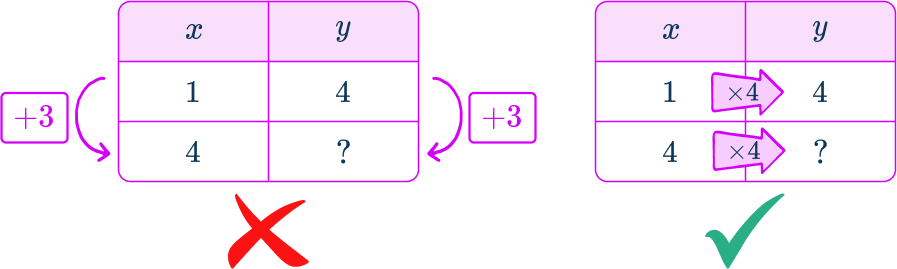

Thinking linear equations are directly proportional
Linear equations are similar to proportions in that they are straight lines and have a constant rate of change (slope). However, unless a linear equation has a $b$ value ( $y$ –intercept) that is equal to $0,$ it is NOT directly proportional.

Mixing up direct and inverse proportion
For direct proportion, the constant of proportionality $k$ is the ratio of the two variables such as $k=y\div{x}.$ For inverse proportion, $k$ is the product of the two variables, such as $k=xy.$

Direct and inverse variation
Direct variation
Inversely proportional
Inverse proportion formula
Directly proportional graph

Practice direct proportion questions

10

35

45

30

$y$ is directly proportional to $x$ so $y=kx.$ At $(3,7),$

\begin{aligned}7&=k\times{3} \\\\ k&=7\div{3}=\cfrac{7}{3}\end{aligned}

So $y=\cfrac{7}{3}x$

When $y=\cfrac{7}{3}\times{15}=7\times{5}=35$

2.5

11

3

5

$y$ is directly proportional to $x$ so $y=kx.$ At $(2,6),$

\begin{aligned}6&=k\times{2} \\\\ k&=6\div{2}=3 \end{aligned}

So $y=3x$

When $y=15,$

\begin{aligned}15&=3\times{x} \\\\ 15&\div{3}=x \\\\ x&=5\end{aligned}

2 \cfrac{1}{2}

6 \cfrac{2}{5}

\cfrac{5}{8}

\cfrac{8}{5}

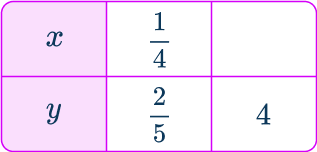
$y$ is directly proportional to $x$ so $y=kx.$ At $\left(\cfrac{1}{4},\cfrac{2}{5}\right),$

\begin{aligned}\cfrac{2}{5}&=k\times\cfrac{1}{4} \\\\ k&=\cfrac{2}{5}\div\cfrac{1}{4}=\cfrac{8}{5} \end{aligned}

So $y=\cfrac{8}{5}x$

When $y=4,$

\begin{aligned}4&=\cfrac{8}{5}\times{x} \\\\ 4&\div\cfrac{8}{5}=x \\\\ x&=2\cfrac{1}{2} \end{aligned}

28,800=k\times{8}

h=3,600s

3,600=k

s=3,600h

The number of hours, $h,$ is proportional to the number of seconds, $s,$ in the same amount of time. This means that $s=kh$ where $k$ is the constant of proportionality. Since $s=28,800$ when $h=8,$

\begin{aligned}28,800&=k\times{8} \\\\ 28,800&\div{8}=k \\\\ k&=3,600 \end{aligned}

Each hour is $3,600$ seconds, so $s=3,600h.$

\$ 359.40

\$ 137.27

\$ 29.95

\$ 38.31

The ticket sales $s$ is directly proportional to the number of people $p.$ This means that $s=kp$ where $k$ is the constant of proportionality. Since $s=1,647.25$ when $p=55,$

\begin{aligned}1,647.25&=k\times{55} \\\\ 1,647.25&\div{55}=k \\\\ k&=29.95 \end{aligned}

Each person pays $\$ 29.95.$

Now $p=12,$ so

\begin{aligned}s&=29.95\times{12} \\\\ s&=359.40 \end{aligned}

$12$ people will generate $\$ 359.40$ in sales.

\$ 26.91

\$ 12.07

\$ 8.97

\$ 22.77

The cost $c$ is directly proportional to the number of pens $p.$ This means that $c=kp$ where $k$ is the constant of proportionality. Since $c=2.07$ when $p=3,$

\begin{aligned}2.07&=k\times{3} \\\\ 2.07&\div{3}=k \\\\ k&=0.69 \end{aligned}

Each pen costs $\$ 0.69.$

Now $p=13,$ so

\begin{aligned}c&=0.69\times{13} \\\\ c&=8.97 \end{aligned}

$13$ pens cost $\$ 8.97.$

Directly proportional FAQs

What is the definition of direct proportionality?

Two variables that are related by a constant relationship or ratio. As one quantity increases or decreases, the other does as well. The proportion equation is $y=kx.$

What is the proportionality symbol?

The symbol $\propto$ represents a proportional relationship.
If $y$ is directly proportional to $x,$ we can write this relationship as: $y\propto{x}$

What are possible $\textbf{x}$ and $\textbf{y}$ values in a proportional relationship?

Proportional relationships can be represented on the coordinate plane, which includes all real numbers. Depending on the context, the values on the $x$ -axis and $y$ -axis can be any subset of real numbers.

For example, if the $x$ -axis represents the number of workers, the $x$ values include all whole numbers. Or, if the $x$ -axis represents the area of a circle, the $x$ values include any real number.

The next lessons are

Converting fractions decimals and percentages
Percent
Compound measure

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.