Multiplicative Inverse - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Multiplication and division Fractions

Math resources Number and quantity Fractions operations

Multiplicative inverse

Here you will learn about the multiplicative inverse, including the definition and how to find it.

Students will first learn about the multiplicative inverse in $6$ th grade math as part of their work in number and operations with fractions when they learn how to divide fractions and extend their knowledge as they work through number systems in middle school.

What is the multiplicative inverse?

The multiplicative inverse of a number is its reciprocal. The multiplicative inverse property states that a number that is multiplied to the original number has a product of $1.$ In other words, a number and its reciprocal will always have a product of $1.$

Let’s take the number $5.$

$5$ has a reciprocal of $\cfrac{1}{5} \, .$

Multiply $5$ and $\cfrac{1}{5} \, , 5 \times \cfrac{1}{5}=\cfrac{5}{5}=1$

$\cfrac{1}{5}$ is the multiplicative inverse of $5.$

To help make sense of a multiplicative inverse, let’s look at visual models.

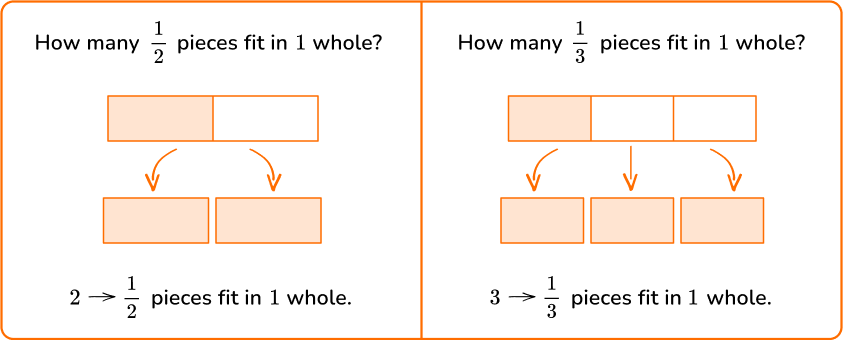
US Web Page_ Multiplicative Inverse 1 US

Do you see a pattern?

$2 \rightarrow \cfrac{1}{2}$

$3 \rightarrow \cfrac{1}{3}$

Not yet? Do you see a pattern now?

$\cfrac{2}{1} \rightarrow \cfrac{1}{2}$

$\cfrac{3}{1} \rightarrow \cfrac{1}{3}$

Can negative numbers have multiplicative inverses?

Let’s look at $-2.$

If you follow the pattern, the reciprocal of $-2$ is $\cfrac{1}{-2}=\cfrac{-1}{2}=-\cfrac{1}{2}$ (the placement of the negative sign can be in the denominator, numerator, or out in front).

$-2 \times \cfrac{1}{-2}=\cfrac{-2}{-2}=\cfrac{2}{2}=1$

The multiplicative inverse of $-2$ is $-\cfrac{1}{2}.$

What is the multiplicative inverse?

Common Core State Standards

How does this apply to $6$ th grade and $7$ th grade math?

Grade 6: Number System (6.NS.A.1)
Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, example, by using visual fraction models and equations to represent the problem.

Grade 7: Number System (7.NS.A.2a)
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as $(-1)(-1)=1$ and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts.

Grade 7: Number System (7.NS.A.2b)
Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If $p$ and $q$ are integers, then $–\left(\cfrac{p}{q}\right) = \cfrac{(–p)}{q} = \cfrac{p}{(–q)} \, .$ Interpret quotients of rational numbers by describing real-world contexts.

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of fraction operations. 10+ questions with answers covering a range of 4th to 6th grade fraction operations topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Fraction Operations Check for Understanding Quiz (Grade 4 to 6)

DOWNLOAD FREE

How to find the multiplicative inverse

In order to write the multiplicative inverse of a number:

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.
“Flip” the fraction by switching the numerator and denominator.
Check to make sure the product is $\bf{1}$ .

Multiplicative inverse examples

Example 1: multiplicative inverse of a whole number

Find the multiplicative inverse of $10$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$10=\cfrac{10}{1}$

2“Flip” the fraction by switching the numerator and denominator.

$\cfrac{10}{1} \rightarrow \cfrac{1}{10}$

$10$ becomes the denominator, and $1$ becomes the numerator.

3Check to make sure the product is $\bf{1}$ .

$\cfrac{10}{1} \times \cfrac{1}{10}=\cfrac{10}{10}=1$

The multiplicative inverse of $10$ is $\cfrac{1}{10} \, .$

Example 2: multiplicative of a fraction number

Find the multiplicative inverse of $\cfrac{4}{7}$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$\cfrac{4}{7} \,$ is a proper fraction.

“Flip” the fraction by switching the numerator and denominator.

$\cfrac{4}{7} \rightarrow \cfrac{7}{4}$

$4$ becomes the denominator, and $7$ becomes the numerator.

Check to make sure the product is $\bf{1}$ .

$\cfrac{4}{7} \times \cfrac{7}{4}=\cfrac{28}{28}=1$

$\cfrac{7}{4} \,$ is the multiplicative inverse of $\cfrac{4}{7} \, .$

Example 3: multiplicative inverse of a mixed fraction

Find the multiplicative inverse of a $1 \cfrac{2}{3}$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$1 \cfrac{2}{3} \rightarrow \cfrac{5}{3}$

“Flip” the fraction by switching the numerator and denominator.

$\cfrac{5}{3} \rightarrow \cfrac{3}{5}$

$5$ becomes the denominator, and $3$ becomes the numerator.

Check to make sure the product is $\bf{1}$ .

$\cfrac{5}{3} \times \cfrac{3}{5}=\cfrac{15}{15}=1$

$\cfrac{3}{5} \,$ is the multiplicative inverse of $\cfrac{5}{3}$ or $1 \cfrac{2}{3}$ .

Example 4: multiplicative inverse of a decimal number

Find the multiplicative inverse of $0.13$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$0.13$ is thirteen hundredths, which is $\cfrac{13}{100}$ .

“Flip” the fraction by switching the numerator and denominator.

$\cfrac{13}{100} \rightarrow \cfrac{100}{13}$

$13$ becomes the denominator, and $100$ becomes the numerator.

Check to make sure the product is $\bf{1}$ .

$\cfrac{13}{100} \times \cfrac{100}{13}=\cfrac{1300}{1300}=1$

$\cfrac{100}{13} \,$ is the multiplicative inverse of $0.13\left(\cfrac{13}{100}\right)$ .

Example 5: multiplicative inverse of a negative number

Find the multiplicative inverse of $-17$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$-17=\cfrac{-17}{1}$

“Flip” the fraction by switching the numerator and denominator.

$\cfrac{-17}{1} \rightarrow \cfrac{1}{-17}$

Check to make sure the product is $\bf{1}$ .

$\cfrac{-17}{1} \times \cfrac{1}{-17}=\cfrac{-17}{-17}=\cfrac{17}{17}=1$

The multiplicative inverse of $-17$ is $\cfrac{1}{-17} \text { or }-\cfrac{1}{17}$ .

Example 6: multiplicative of a negative fraction

Find the multiplicative inverse of $-1 \cfrac{2}{9}$ .

If the number is a whole number, mixed number, decimal, or integer, write it as an improper fraction.

$-1 \cfrac{2}{9}=\cfrac{-11}{9}$

“Flip” the fraction by switching the numerator and denominator.

$\cfrac{-11}{9} \rightarrow \cfrac{9}{-11}$

$-11$ becomes the denominator, and $9$ becomes the numerator.

The placement of the negative number can be out in front of the fraction, $-\cfrac{9}{11}$

Check to make sure the product is $\bf{1}$ .

$\cfrac{-11}{9} \times \cfrac{9}{-11}=\cfrac{-99}{-99}=\cfrac{99}{99}=1$

$-\cfrac{9}{11}$ is the multiplicative inverse of $-1 \cfrac{2}{9}\left(\cfrac{-11}{9}\right).$

Teaching tips for multiplicative inverse

Reinforce that the multiplicative inverse is also the reciprocal.

Have students discover the multiplicative inverse of numbers on their own by strategically asking questions such as, “what number multiplied to $5$ will give a product of $1?”$

When working with multiplicative inverse, have students see that the reciprocal of a unit fraction is a whole number.

Although worksheets serve a purpose in the classroom and can help with skill practice and test prep practice, having students discover the mathematical concepts is more meaningful for building long lasting understanding.

Provide students with calculators or multiplication tables so that they do not get frustrated making calculations, but rather develop an understanding of the topic.

Easy mistakes to make

Trying to find the reciprocal of zero
Zero does not have a reciprocal. This is because we can think about $0$ as being $\cfrac{0}{1}.$ When the numerator and the denominator are flipped it becomes $\cfrac{1}{0}$ or $1 \div 0$ which is undefined (it does not exist).

Forgetting that a whole number can be written as an improper fraction
Whole numbers can be written as improper fractions. For example, $10$ can be written as $\cfrac{10}{1}.$

Practice multiplicative inverse questions

1.33

-\cfrac{1}{33}

\cfrac{1}{33}

0.33

Write $33$ as an improper fraction, $33=\cfrac{33}{1}$

Flip the numerator and the denominator. $33$ becomes the denominator and $1$ becomes the numerator. Check that the product of the number and its multiplicative inverse is $1.$

$\cfrac{33}{1} \times \cfrac{1}{33}=\cfrac{33}{33}=1$

10.13

\cfrac{13}{10}

13.10

-\cfrac{13}{10}

$\cfrac{10}{13} \,$ is already a proper fraction.

Flip the numerator and the denominator. $10$ becomes the denominator and $13$ becomes the numerator. Check that the product of the number and its multiplicative inverse is $1.$

$\cfrac{10}{13} \times \cfrac{13}{10}=\cfrac{130}{130}=1$

The multiplicative inverse of $\cfrac{10}{13} \,$ is $\cfrac{13}{10}$ .

11

-11

​​\cfrac{1}{11}

-\cfrac{1}{11}

The multiplicative inverse of $-11$ when multiplied to $-11$ will make the product equal to $1.$

Make $-11$ into a fraction, $\cfrac{-11}{1} \, .$

Flip the numerator and the denominator. $-11$ becomes the denominator and $1$ becomes the numerator.

The multiplicative of $-11$ is $\cfrac{1}{-11}$ or $-\cfrac{1}{11} \, .$

$\cfrac{-11}{1} \times \cfrac{1}{-11}=\cfrac{-11}{-11}=\cfrac{11}{11}=1$

3 \cfrac{3}{7}

\cfrac{24}{7}

-\cfrac{7}{24}

\cfrac{7}{27}

$-3 \cfrac{3}{7} \,$ change to an improper fraction, $\cfrac{-24}{7}$

Flip the numerator and the denominator. $-24$ becomes the denominator and $7$ becomes the numerator.

The multiplicative inverse is $\cfrac{7}{-24}$ or $-\cfrac{7}{24}$ .

$\cfrac{-24}{7} \times \cfrac{7}{-24}=\cfrac{-168}{-168}=\cfrac{168}{168}=1$

1.27

\cfrac{100}{27}

\cfrac{27}{100}

\cfrac{-27}{100}

Change $0.27$ to a fraction, $\cfrac{27}{100}.$

Flip the numerator and the denominator.

$27$ becomes the denominator and $100$ becomes the numerator, $\cfrac{100}{27} \, .$

$\cfrac{27}{100} \times \cfrac{100}{27}=\cfrac{2700}{2700}=1$

The multiplicative inverse of $0.27 \left(\cfrac{27}{100}\right)$ is $\cfrac{100}{27}.$

-\cfrac{10}{51}

-\cfrac{31}{10}

5.1

1.5

Change $-5.1$ to an improper fraction.

$-5.1=-5 \cfrac{1}{10}=\cfrac{-51}{10}$

Flip the numerator and the denominator.

$-51$ becomes the denominator and $10$ becomes the numerator.

The multiplicative inverse of $-5.1\left(\cfrac{-51}{10}\right)$ is $-\cfrac{10}{51} \, .$

$\cfrac{-51}{10} \times \cfrac{10}{-51}=\cfrac{-510}{-510}=\cfrac{510}{510}=1$

Multiplicative inverse FAQs

Is there a multiplicative inverse of any real number or complex number?

Rational numbers (natural numbers, whole numbers, integers, fractions/decimals) and irrational numbers have multiplicative inverses. The only number that does not have a multiplicative inverse is $0.$
The multiplicative inverse of any number a is $\cfrac{1}{a} \, .$
For example, the multiplicative inverse of $5$ can be written as $1 \div 5$ or $\cfrac{1}{5} \, .$
$5 \times \cfrac{1}{5}=1 \, .$ $\Pi$ is an irrational number.
The multiplicative inverse of $\Pi$ is $1 \div \Pi$ or $\cfrac{1}{\Pi} \, . \; \Pi \times \cfrac{1}{\Pi}=1.$
To find the multiplicative inverse of $0$ is $1 \div 0$ or $\cfrac{1}{0} \,$ which does not exist because you cannot divide by $0.$

Complex numbers, which you will study in great depth in an Algebra $2$ class, also have multiplicative inverses.
The complex number $z$ has $\cfrac{1}{z} \,$ as its multiplicative inverse. All types of numbers have multiplicative inverses.

Can you find the multiplicative inverse of a multiplicative inverse?

Yes, if you find the multiplicative inverse of a multiplicative inverse, you will wind up back at the original given number.
For example, the multiplicative inverse of $5$ (written as $\cfrac{5}{1} \,$ ) is $\cfrac{1}{5}.$
If you then take the multiplicative inverse of $\cfrac{1}{5} \, ,$ it will be $\cfrac{5}{1}$ or $5. \; 5$ is the original given number.

Is the multiplicative inverse of a number just turning the fraction upside down?

The multiplicative inverse of a number is always a number that when multiplied by the original number gives a product of $1.$ So, it is often just flipping the fraction around.

What is the reciprocal of a number?

The reciprocal of a number is the multiplicative inverse.

What is the multiplicative identity?

The multiplicative identity is $1$ because a number times $1$ has a product of that number.

What is the additive inverse?

The additive inverse is a number when added to the original number has a sum of $0.$ For example, the additive inverse of $5$ is $-5$ because $5+(-5)=0.$

What is an extended euclidean algorithm?

The euclidean algorithm or extended euclidean algorithm is used for finding the greatest common divisor (gcd) between two positive numbers and writing the gcd as an integer linear combination. This is something explored in an advanced high school or college level.

What is modular arithmetic?

Modular arithmetic is studied in advanced high school and college courses and is a branch of arithmetic where the only concern is with the remainder after dividing two numbers.

There is an operator that is used to determine the remainder of a division operation called the modulus operator or the modulo operator.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.