High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplication and divisionUnderstanding multiplication
Understanding division
Long division
Here you will learn about long division, including how to divide using long division and solving for quotients with and without remainders.
Students will first learn about long division as part of the number system in grade 6 and will continue to use the skill throughout middle school and high school.
What is long division?
Long division, also known as the standard algorithm, is a standardized process used to divide multi-digit numbers, by breaking the multiplication into a sequence of steps.
Before performing long division, you must first understand the different parts of a division equation:
- The dividend is the number that is being divided equally.
- The divisor is the number that divides the dividend. It is also thought of as the number of items in each group, or the number of groups.
- The quotient is the answer of the division process. In some cases, there may be a remainder included with the quotient.
For example, if we were to divide 120 \div 6,

How to divide using long division
In order to divide using long division, first identify the dividend and divisor. You will write the dividend under a division bracket, with the divisor to the left.
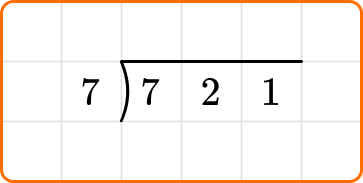
You will then start a sequence of steps that include dividing, multiplying and subtraction. These steps can be done once, or many times, depending on the size of the divisor and dividend.
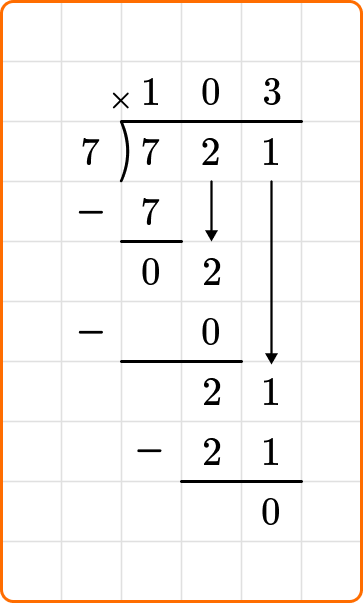
Divide: First, calculate how many times the divisor 7 can divide into the first digit of the dividend, 7.
7 \div 7=1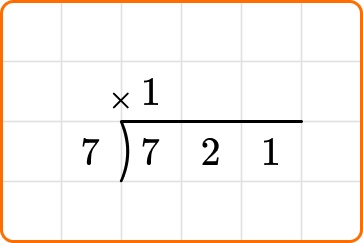
Multiply: The 1 will be placed above the top line of the division bracket, and multiplied by the divisor, 7.
7 \times 1=7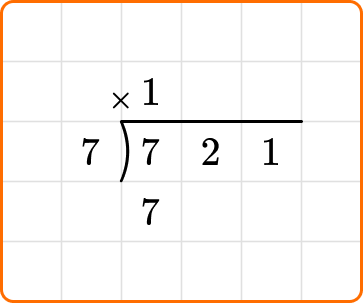
Subtract: Place this number under the first number in the hundreds place, 7 and subtract.
7-7=0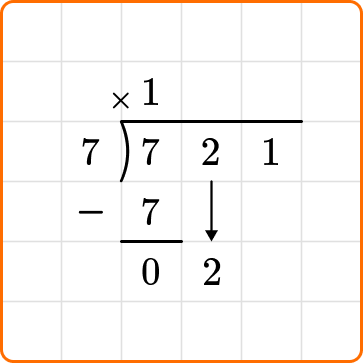
Bring down the next number from the dividend, and continue dividing until all numbers in the dividend have been brought down.
![[FREE] Long Division Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Long-Division-Worksheet-listing-image.png)
[FREE] Long Division Worksheet (Grade 6 to 7)
![[FREE] Long Division Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Long-Division-Worksheet-listing-image.png)
Use this worksheet to check your 6th to 7th grade students’ understanding of long division. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Long Division Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Long-Division-Worksheet-listing-image.png)
[FREE] Long Division Worksheet (Grade 6 to 7)
![[FREE] Long Division Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Long-Division-Worksheet-listing-image.png)
Use this worksheet to check your 6th to 7th grade students’ understanding of long division. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEQuotients with remainders
Sometimes the dividend cannot be equally divided into by the divisor. When this happens, you would be left with a remainder. You may see a remainder in different formats:
- As a whole number
- As a decimal
- As a fraction
Students in upper grade levels are often taught to leave the reminders as either whole numbers or fractions. As students move into long division in middle school, students will be expected to express their remainders as fractions.
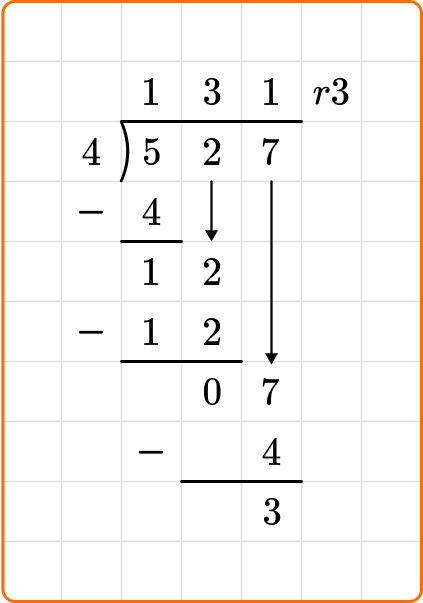
If you divide 527 \div 4, you will end up with a remainder of 3. Let’s look at how you can show the remainder of 3 in all three ways:
Remainders as a whole number
When you leave the remainder as a whole number, you will write a lowercase r to the right of the quotient, and place the remainder after.
For example,
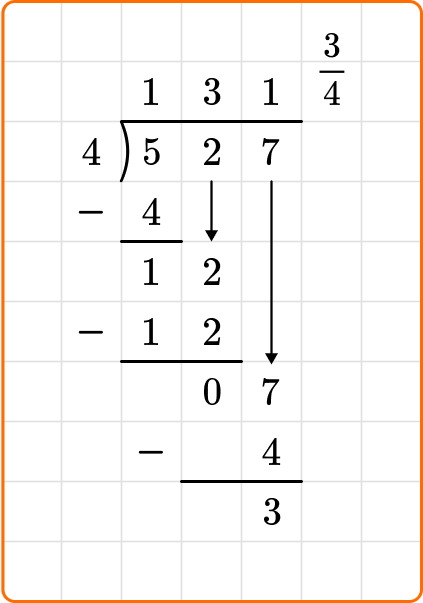
Remainders as a fraction
When you leave your remainder as a fraction, you will write the remainder as the numerator, and the divisor as the denominator.
For example,
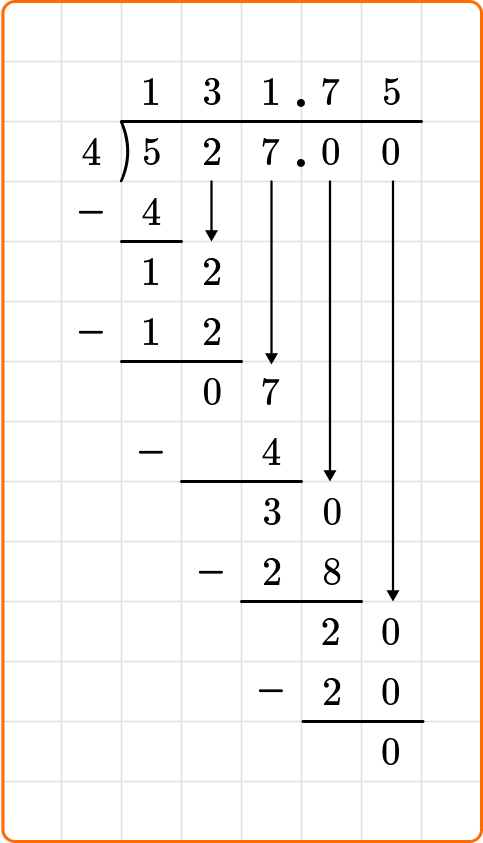
Remainder as a decimal
When asked to leave your remainder as a decimal, you will continue dividing. First, you will place a decimal to the left of the ones place of the dividend, as well as in the quotient. After the decimal place next to the dividend, place a zero.
You will then bring that zero down, as you had all the digits from the dividend, and continue dividing until you get a remainder of zero.
For example,
What is long division?

Common Core State Standards
How does this relate to 6 th and 7 th grade math?
- Grade 6 – The Number System (6.NS.B.2)
Fluently divide multi-digit numbers using the standard algorithm.
- Grade 7 – The Number System (7.NS.A.2d)
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats.
How to divide using long division
In order to divide using long division, you need to:
- Set up the division equation using a division bracket.
- Divide, multiply and subtract.
- Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.
- State your answer.
Long division examples
Example 1: long division without remainders
Solve 672 \div 6.
- Set up the division equation using a division bracket.
Write the dividend, 672, inside the division bracket, and the divisor, 6, out to the left of the division bracket.
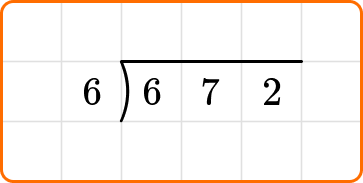
2Divide, multiply and subtract.
Ask yourself: How many times does 6 go into the first digit of the dividend 6?
Divide: 6 \div 6=1
Write the number 1 above the long division symbol.
Multiply: 6 \times 1=6
Write the result beneath the dividend.
Subtract: 6-6=0
Bring down the next digit of the dividend, the 7.
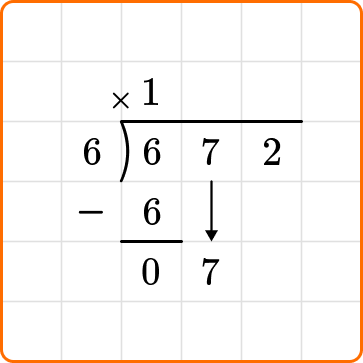
3Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor.
Ask yourself: How many times does 6 go into 7?
Divide: 7 \div 6=1
Write the number 1 above the long division symbol.
Multiply: 6 \times 1=6
Write the result beneath the dividend.
Subtract: 7-6=1
Bring down the next digit of the dividend, 2, beside the 1.
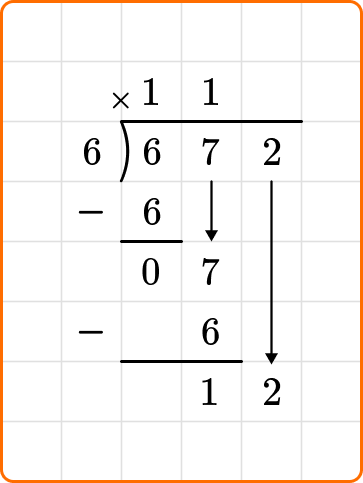
12 is larger than the divisor 6, so continue dividing.
Ask yourself: How many times does 6 go into 12?
Divide: 12 \div 6=2
Write the number 2 above the long division symbol.
Multiply: 6 \times 2=12
Write the result beneath the dividend.
Subtract: 12-12=0
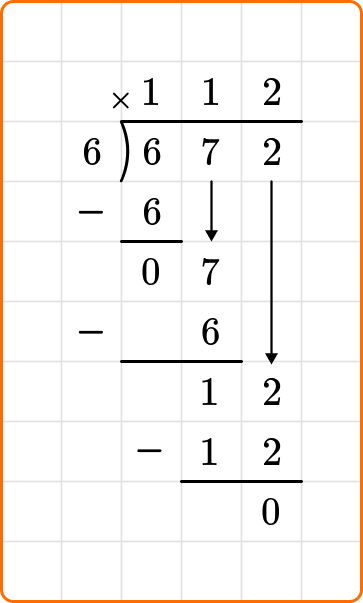
There is no remaining value to divide, so you are done dividing. The quotient is the number on the top of the division bracket.
4State your answer.
672 \div 6=112Example 2: long division without remainders
Solve 9,240 \div 30.
Write the dividend, 9,240, inside the division bracket, and the divisor, 30, out to the left of the division bracket.
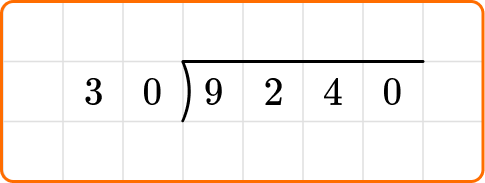
Ask yourself: How many times can 30 go into 92?
Divide: 92 \div 30=3
Write the number 3 above the long division symbol.
Multiply: 30 \times 3=90
Write the result beneath the dividend.
Subtract: 92-90=2
Bring down the next digit of the dividend, 4, beside the 2.
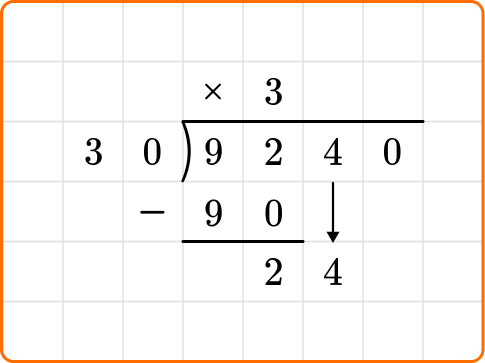
Ask yourself: How many times does 30 go into 24?
Divide: 24 \div 30=0
Write the number 0 above the long division symbol.
Multiply: 30 \times 0=0
Write the result beneath the dividend.
Subtract: 24-0=24
Bring down the remaining dividend, 0, and you are left with 240.

240 is larger than the divisor 30, so continue dividing.
Ask yourself: How many times 30 goes into 240?
Divide: 240 \div 30=8
Write the number 8 above the long division symbol.
Multiply: 30 \times 8=240
Write the result beneath the dividend.
Subtract: 240-240=0
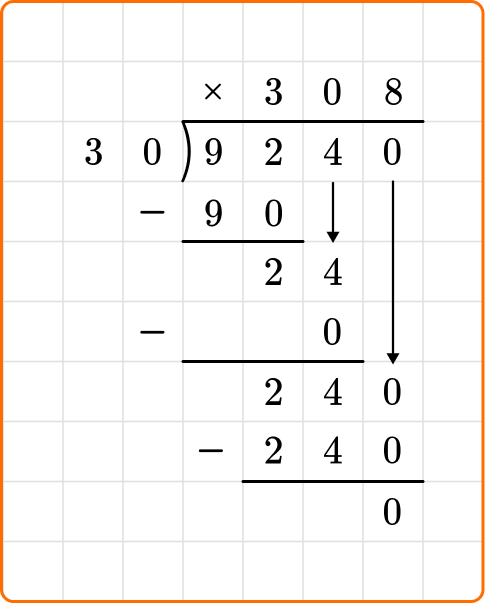
There is no remaining value to divide, so you are done dividing. The quotient is the number on the top of the division bracket.
Example 3: long division with whole number remainders
Solve 763 \div 28. Write the remainder as a whole number.
Write the dividend, 763, inside the division bracket, and the divisor, 28, out to the left of the division bracket.
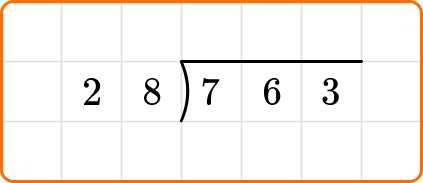
Ask yourself: How many times does 28 go into the first two digits of the dividend, 76?
Divide: 76 \div 28=2
Write the number 2 above the long division symbol.
Multiply: 28 \times 2=56
Write the result beneath the dividend.
Subtract: 76-56=20
Bring down the next digit of the dividend, the 3.
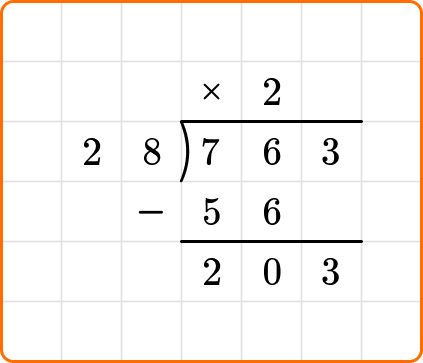
Ask yourself: How many times does 28 go into 203?
Divide: 203 \div 28=7
Write the number 7 above the long division symbol.
Multiply: 28 \times 7=196
Write the result beneath the dividend.
Subtract: 203-196=7
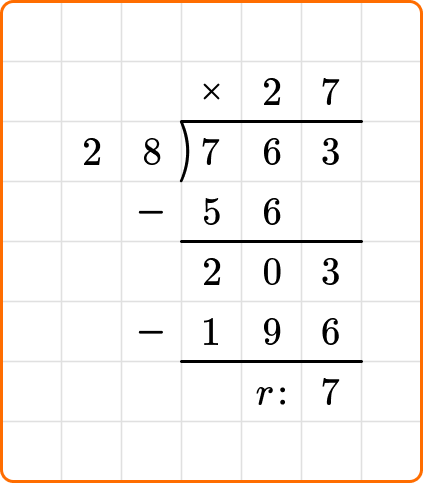
7 is less than the divisor 28, so you are finished dividing.
The question states to write your remainder as a whole number.
763 \div 28=27 \; r7
Example 4: long division with remainders as fractions
Solve 167 \div 8. Write your remainder as a fraction.
Write the dividend, 167, inside the division bracket, and the divisor, 8, out to the left of the division bracket.
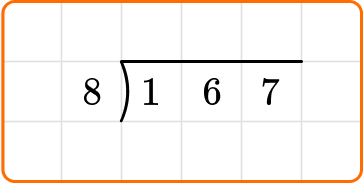
Ask yourself: How many times does 8 go into the first two digits of the dividend, 16?
Divide: 16 \div 8=2
Write the number 2 above the long division symbol.
Multiply: 8 \times 2=16
Write the result beneath the dividend.
Subtract: 16-16=0
Bring down the next digit of the dividend, 7, beside the 0.
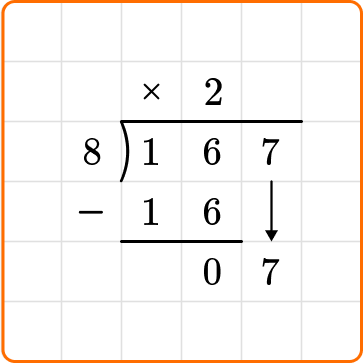
Ask yourself: How many times does 8 go into 7?
Divide: 7 \div 8=0
Write the number 0 above the long division symbol.
Multiply: 0 \times 8=0
Write the result beneath the dividend.
Subtract: 7-0=7
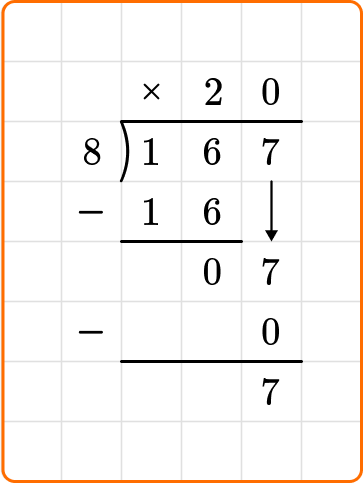
7 is less than 8, so you are done dividing.
To write your remainder as a fraction, the remainder is the numerator and the divisor becomes your denominator.
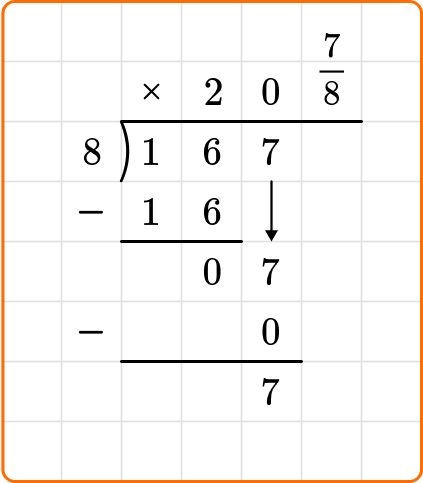
The question states to write your remainder as a fraction.
167 \div 8=20 \cfrac{7}{8}
Example 5: long division with a decimal remainder
Solve 53 \div 4. Write your remainder as a decimal.
Write the dividend, 53, inside the division bracket, and the divisor, 4, out to the left of the division bracket.
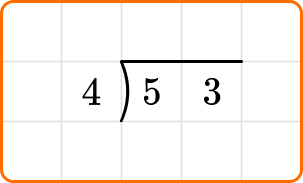
Ask yourself: How many times does 4 go into the first digit of the dividend, 5?
Divide: 5 \div 4=1
Write the number 1 above the long division symbol.
Multiply: 4 \times 1=4
Write the result beneath the dividend.
Subtract: 5-4=1
Bring down the next digit of the dividend, the 3.
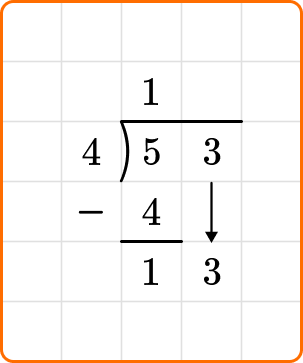
Ask yourself: How many times does 4 go into 13?
Divide: 13 \div 4=3
Write the number 3 above the long division symbol.
Multiply: 4 \times 3=12
Write the result beneath the dividend.
Subtract: 13-12=1
Because the problem states to write the remainder as a decimal, you will keep dividing, even though the remainder is less than the divisor.
You will add a decimal point after the 3 in 53, followed by a 0. Make sure to write the decimal point above the division bracket too. Bring the zero down next to the 1 and continue dividing.
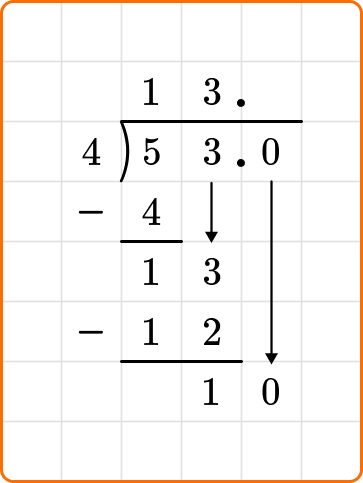
Ask yourself: How many times does 4 go into 10?
Divide: 10 \div 4=2
Write the number 2 above the division symbol, to the right of the decimal point.
Multiply: 4 \times 2=8
Write the result beneath the dividend.
Subtract: 10-8=2
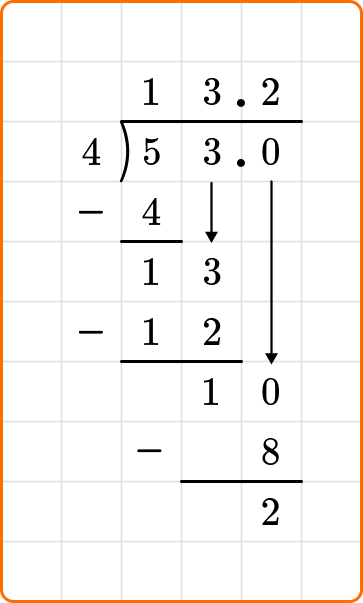
You will repeat the process of adding another zero to the dividend and bring it down until you have a zero after subtracting.
Ask yourself: How many times does 4 go into 20?
Divide: 20 \div 4=5
Write the number 5 above the long division symbol.
Multiply: 4 \times 5=20
Write the result beneath the dividend.
Subtract: 20-20=0
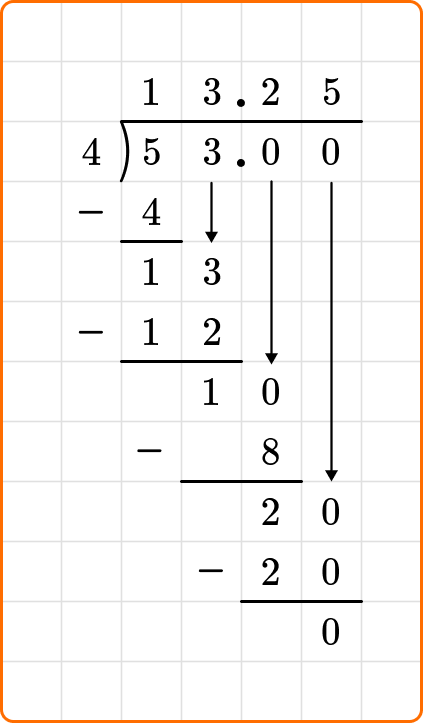
The problem states to write your remainder as a decimal.
53 \div 4=13.25
Example 6: long division word problem
Cassie received \$1,260 for her graduation. She wants to spend the money equally over the next 6 months. How much money can Cassie spend each month?
Write the dividend, 1,260, inside the division bracket, and the divisor, 6, out to the left of the division bracket.
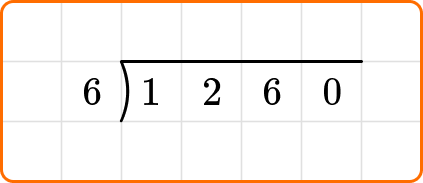
Ask yourself: How many times does 6 go into 12?
Divide: 12 \div 6=2
Write the number 2 above the long division symbol.
Multiply: 6 \times 2=12
Write the result beneath the dividend.
Subtract: 12-12=0
Bring down the next digit of the dividend, the 6.
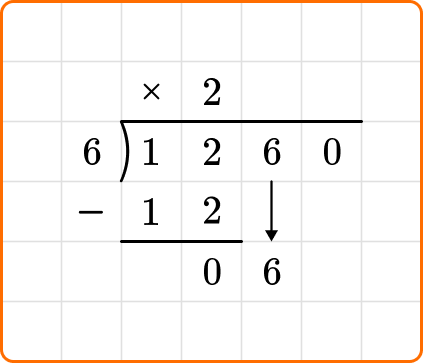
Ask yourself: How many times does 6 go into 6?
Divide: 6 \div 6=1
Write the number 1 above the long division symbol.
Multiply: 6 \times 1=6
Write the result beneath the dividend.
Subtract: 6-6=0
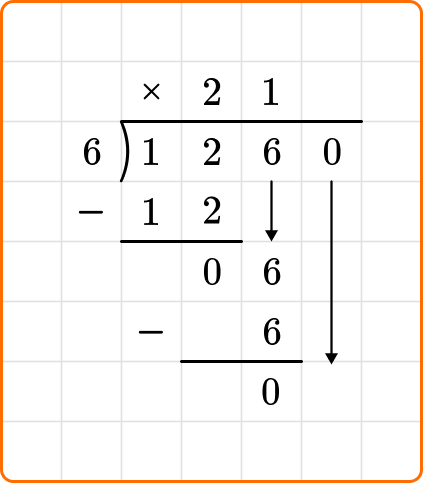
Ask yourself: How many times does 6 go into 0?
Divide: 6 \div 0=0
Write the number 0 above the long division symbol.
Multiply: 6 \times 0=0
Write the result beneath the dividend.
Subtract: 0-0=0
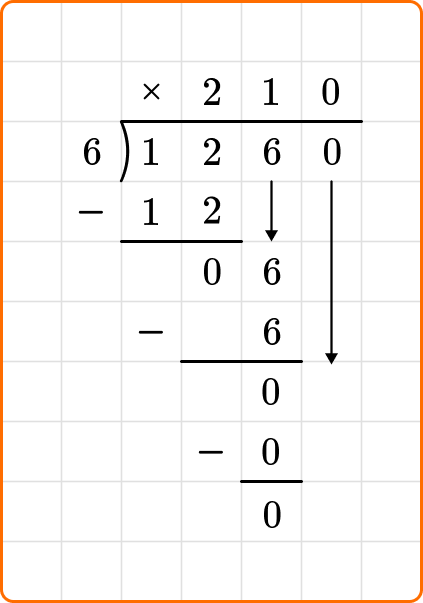
Cassie can spend \$210 each month.
1260 \div 6=210
Teaching tips for long division
- Make sure students have a firm grasp on how to divide using partial quotients, as it helps students visualize why the long division method works.
- If using long division worksheets, start with simple long division problems, such as dividing by one digit divisors with no remainders. Once students begin grasping the concept of long division, increase the challenge of the problems, including large numbers.
- Emphasize paying attention to the place value of each digit as they set up and solve the problem. Allowing students to use graph paper when first beginning long division will allow them to easily organize their math, especially when working with larger numbers.
- Providing the students with step-by-step division steps allows them to refer back to them as needed. These can be displayed within the classroom on an anchor chart or in their math journals.
- Allow students to check their answers using a long division calculator. This allows real time feedback for students so they do not continue to practice the long division algorithm incorrectly.
Easy mistakes to make
- Forgetting to bring down the next number
Students will divide the first set of numbers correctly but may forget they need to bring down the next digit from the dividend to continue dividing. Having an example of a complete long division problem will give students something to refer back to.
- Alignment issues
Proper placement of numbers is important and can lead to calculation errors if the work is not organized. Allowing students to use graph paper is one way to assist with this.
Related multiplication and division lessons
Practice long division questions
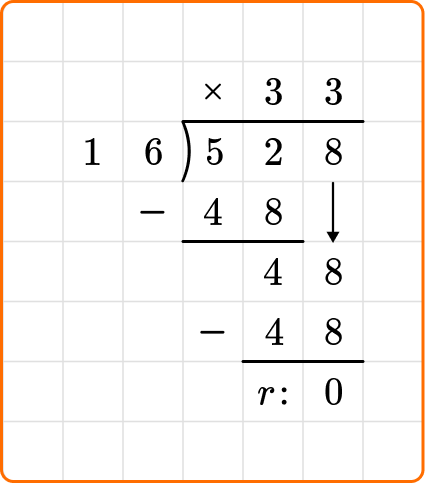
1. Solve 528 \div 16.




Set up your division equation with the dividend, 528, inside the division bracket and the divisor, 16, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 16.
2. Divide 237 \div 9.




Set up your division equation with the dividend, 237, inside the division bracket and the divisor, 9, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 9.
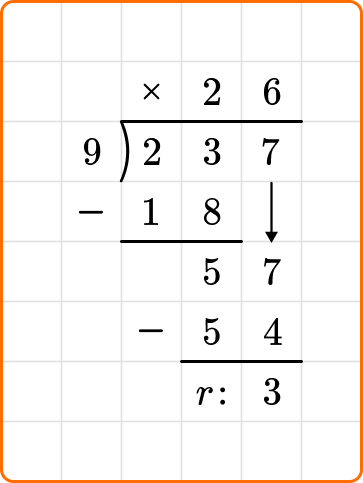
3. Solve 648 \div 12.




Set up your division equation with the dividend, 648, inside the division bracket and the divisor, 12, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 12.
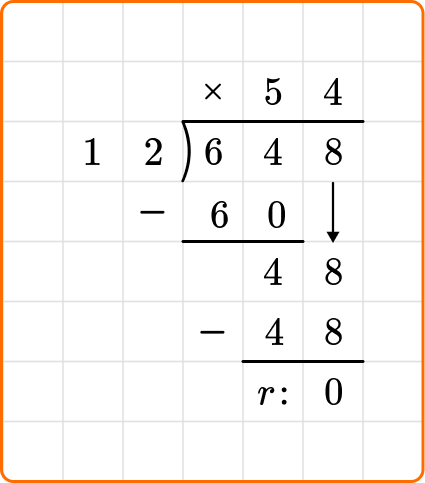
4. Solve 489 \div 15. Write the quotient as a decimal.




Set up your division equation with the dividend, 489, inside the division bracket and the divisor, 15, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a decimal.

5. Solve 357 \div 8. Write the quotient as a fraction.




Set up your division equation with the dividend, 357, inside the division bracket and the divisor, 8, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0, leaving your remainder as a fraction.

6. Mrs. Davis had 112 pencils to divide into 9 pencil boxes. How many pencils did Mrs. Davis put in each pencil box?
4 pencils

12 pencils

11 pencils

15 pencils

Set up your division equation with the dividend, 112, inside the division bracket and the divisor, 9, to the left.
Proceed with the steps, dividing, multiplying and subtracting until the remainder is 0 or less than 9.
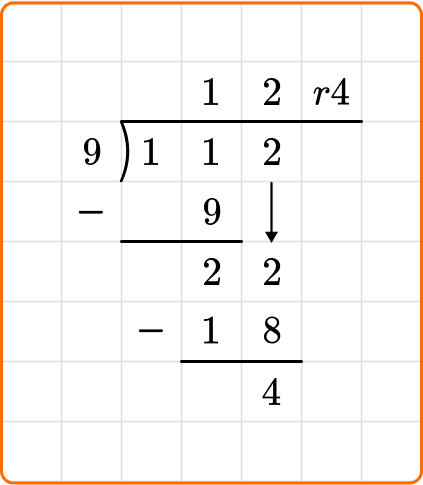
Mrs. Davis can equally place 12 pencils in each pencil box and will have 4 pencils left over.
Long division FAQs
The number of decimal places will vary by division problem. Some division problems will only have one decimal place, while others will have many.
The long division symbol is sometimes called a division bracket, but does not have an established name.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!