High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Similar shapes
Here you will learn about similar shapes, including what they are and how to identify them.
Students will first learn about similar shapes as part of geometry in 8 th grade.
What are similar shapes?
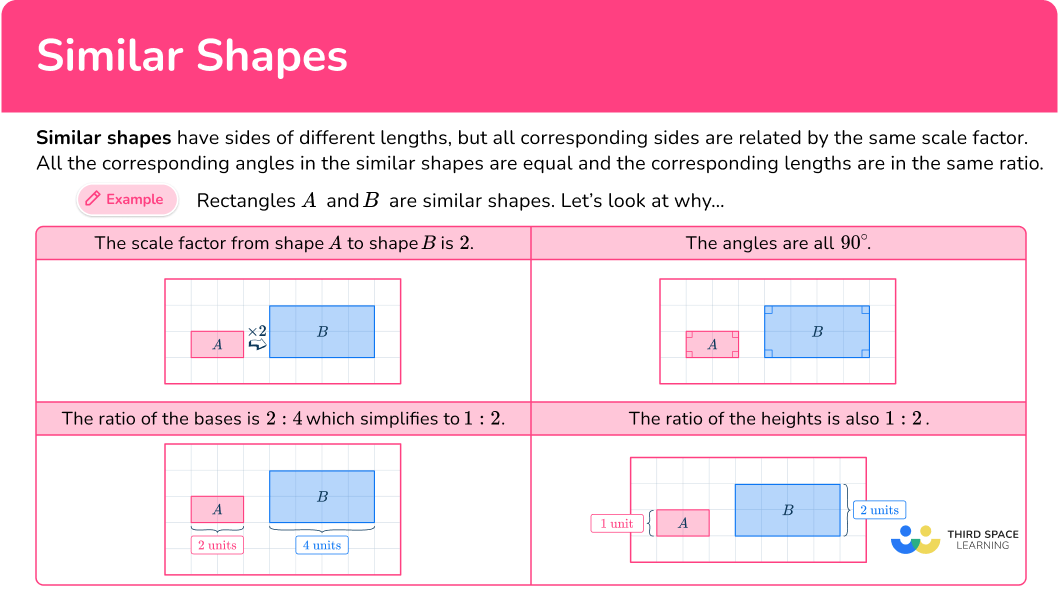
Similar shapes have sides of different lengths, but all corresponding sides are related by the same scale factor. All the corresponding angles in the similar shapes are equal and the corresponding lengths are in the same ratio.
For example, these two rectangles are similar shapes because:
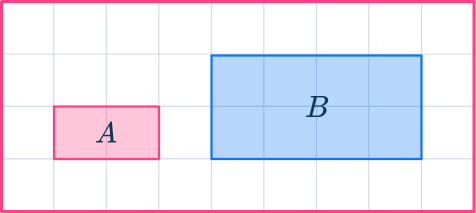
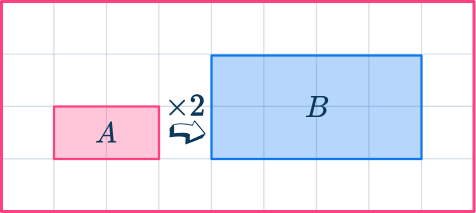
- The scale factor from shape A to shape B is 2.
- The ratio of the bases is 2\text{:}4 which simplifies to 1\text{:}2.
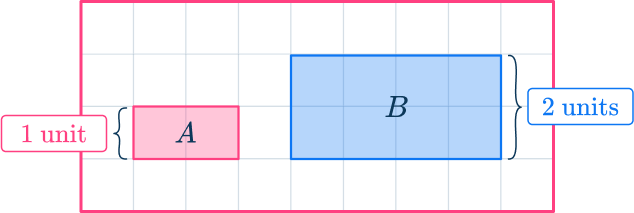
- The ratio of the heights is also 1\text{:}2.
NOTE: Since the opposite sides of a rectangle are congruent, by comparing the base and the height, you have compared all sides of the rectangle.
- The angles are all 90^{\circ}.
What are similar shapes?
Common Core State Standards
How does this relate to 8 th grade math?
- Grade 8: Geometry (8.G.A.2)
Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
![[FREE] 2D Shape Worksheet (Grade 2 to 4)](https://thirdspacelearning.com/wp-content/uploads/2023/07/2D-shapes-check-for-understanding-quiz-listing-image.png)
[FREE] 2D Shape Worksheet (Grade 2 to 4)
Use this quiz to check your grade 2 to 4 students’ understanding of 2D shape. 15+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] 2D Shape Worksheet (Grade 2 to 4)
Use this quiz to check your grade 2 to 4 students’ understanding of 2D shape. 15+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!
DOWNLOAD FREEHow to decide if shapes are similar
In order to decide if shapes are similar:
- Decide which sides are pairs of corresponding sides.
- Find the ratios of the sides.
- Check if the ratios are the same.
Similar shapes examples
Example 1: identifying similar rectangles
Are these shapes similar?
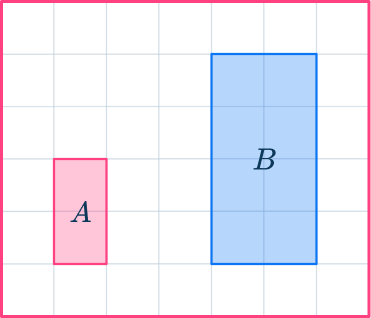
- Decide which sides are pairs of corresponding sides.
The bases of the rectangles are a pair of corresponding sides.
The heights of the rectangles are a pair of corresponding sides.
2Find the ratios of the sides.
When writing the ratios, the order is very important.
Here the ratio is \text{length }A\text{:}\text{ length }B .
The ratio of the bases is 1\text{:}2.
The ratio of the heights is 2\text{:}4, which simplifies to 1\text{:}2.
3Check if the ratios are the same.
The ratios for the corresponding lengths are the same.
The scale factor from shape A to shape B is 2.
The rectangles are similar shapes.
Example 2: identifying similar triangles
Are these shapes similar?
Decide which sides are pairs of corresponding sides.
The bases of the triangles are a pair of corresponding sides.
The heights of the triangles are a pair of corresponding sides.
The right angles are corresponding angles.
NOTE: For right triangles, you can just compare the base and height, without considering the hypotenuse.
Find the ratios of the sides.
When writing the ratios the order is very important.
The ratio of the heights is 5\text{:}15, which simplifies to 1\text{:}3.
The ratio of the bases is 7\text{:}20. This can be written as 1\text{:}\cfrac{20}{7} or 1\text{:}2.857…
Check if the ratios are the same.
The ratios for the corresponding lengths are NOT the same.
The triangles are NOT similar shapes.
NOTE: This example shows the importance of proving similarity mathematically. Just glancing at these right triangles, they may appear to be similar. However, when you solve for the ratio of their sides, you see that they are not (though they are very close to be similar!)
How to find a missing length
In order to find a missing side in a pair of similar shapes:
- Decide which sides are pairs of corresponding sides.
- Find the scale factor.
- Use the scale factor to find the missing length.
Missing length examples
Example 3: finding a missing length on a quadrilateral
Here are two similar shapes. Find the length QR.
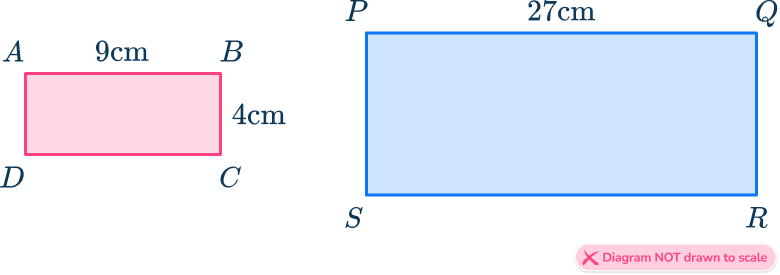
Decide which sides are pairs of corresponding sides.
Identify the corresponding sides that have measurements and those mentioned in the question.
- The sides AB and PQ are a pair of corresponding sides.
- The sides BC and QR are a pair of corresponding sides.
There are other corresponding sides, but you do not need them to answer the question.
Find the scale factor.
The ratio of the lengths AB\text{:}PQ is 9\text{:}27 which simplifies to 1\text{:}3.
This means scale factor from rectangle PQRS to ABCD is \cfrac{1}{3} and the scale factor from rectangle ABCD to PQRS is 3.
Use the scale factor to find the missing length.
The ratio of the lengths BC\text{:}QR is also 1\text{:}3.
Use the scale factor 3 as a multiplier to find the missing length.
The missing side has been found to be QR=12\mathrm{~cm}.
Alternatively, an equation may be formed and solved:
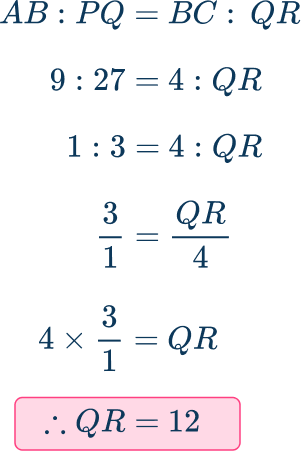
Example 4: finding a missing length
Here are two similar triangles. Find the length BC.
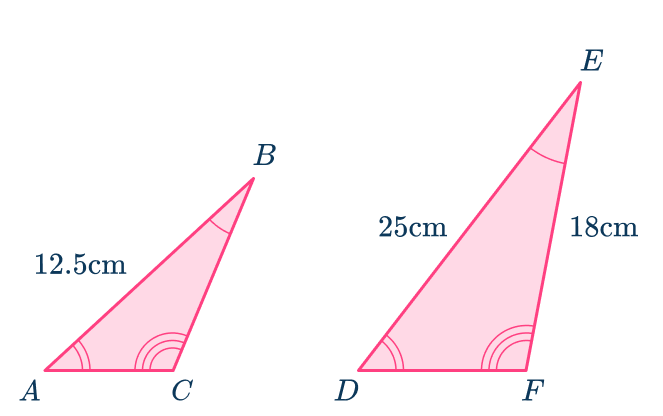
Decide which sides are pairs of corresponding sides.
Identify the corresponding sides that have measurements and those mentioned in the question.
- The sides AB and DE are a pair of corresponding sides.
- The sides BC and EF are a pair of corresponding sides.
There are other corresponding sides, but you do not need them to answer the question.
Find the scale factor.
The ratio of the lengths AB\text{:}DE is 12.5\text{:}25 which simplifies to 1\text{:}2.
This scale factor from triangle DEF to ABC is \cfrac{1}{2} and the scale factor from triangle ABC to DEF is 2.
But we want a scale factor from DEF to ABC which will be \cfrac{1}{2}.
Use the scale factor to find the missing length.
The ratio of the lengths BC\text{:}EF is also 1\text{:}2.
Use the scale factor \cfrac{1}{2} as a multiplier to find the missing length.
The missing side is BC=9\mathrm{~cm}.
Alternatively, an equation may be formed and solved:
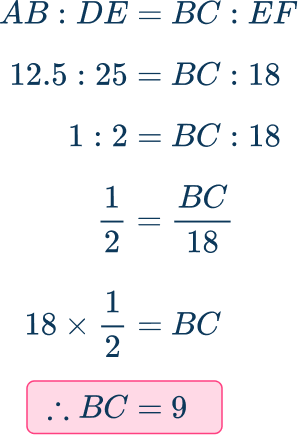
How to find a missing length in a triangle
In order to find a missing side in a pair of triangles when you are not told that the triangles are similar:
- Use angle facts to determine which angles are equal.
- Redraw the triangles side by side.
- Decide which sides are pairs of corresponding sides.
- Find the scale factor.
- Use the scale factor to find the missing length.
Missing length in a triangle examples
Example 5: finding a missing length in a triangle
Find the value of x.
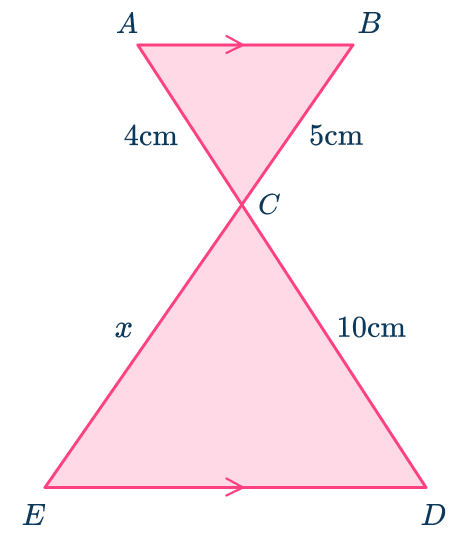
Use angle facts to determine which angles are equal.
Look for equal angles.
\angle{ACB}=\angle{DCE} given that vertically opposite angles are equal.
There are a pair of parallel sides; AB and DE. This means that there are equal angles since there are alternate angles.
\angle{ABC}=\angle{CED} (alternate angles)
\angle{BAC}=\angle{CDE} (alternate angles)
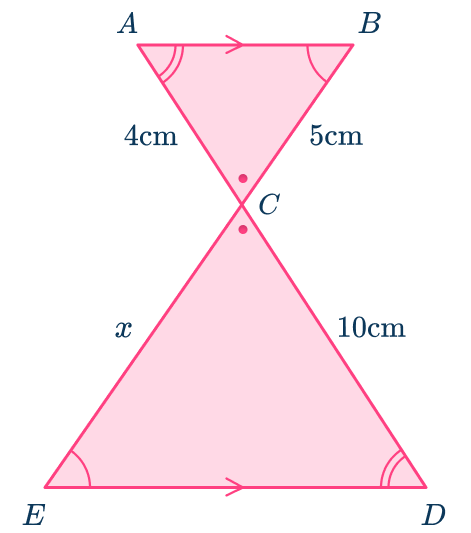
Redraw the triangles side by side.
Redraw the triangles side-by-side so that it is easier to identify the corresponding sides.
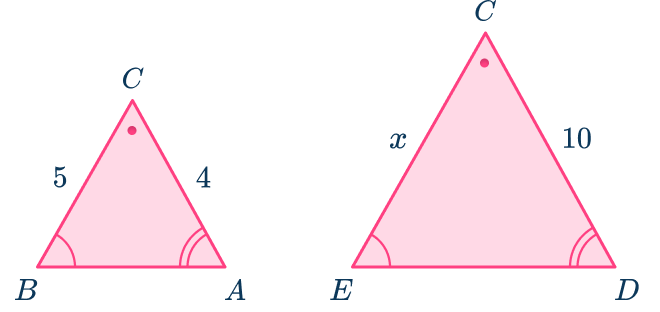
Decide which sides are pairs of corresponding sides.
Identify the corresponding sides that have measurements and those mentioned in the question. Use the angles to help you.
- The sides AC and CD are a pair of corresponding sides.
- The sides BC and CE are a pair of corresponding sides.
There are other corresponding sides, but you do not need them to answer the question.
Find the scale factor.
The ratio of the lengths AC\text{:}CD is 4\text{:}10 which simplifies to 1\text{:}2.5.
This is a scale factor from triangle CDE to ABC of 0.4 and a scale factor from triangle ABC to CDE of 2.5.
Use the scale factor to find the missing length.
The ratio of the lengths BC\text{:}CE is also 1\text{:}2.5.
Use the scale factor 2.5 as a multiplier to find the missing length.
The value of x has been found, x=12.5.
Alternatively, an equation may be formed and solved:
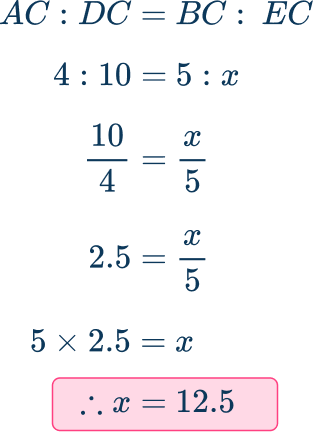
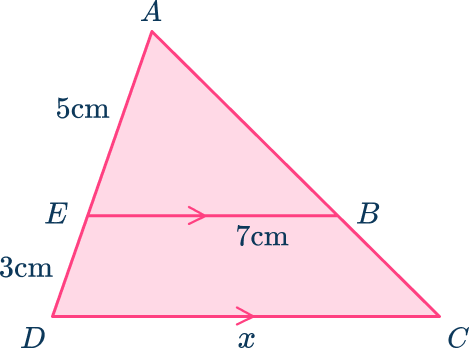
Example 6: finding a missing length in a triangle
Find the value of x.
Use angle facts to determine which angles are equal.
Look for equal angles.
\angle{EAB}=\angle{DAC} as they are common to both triangles.
There are a pair of parallel sides – BE and CD. This means that there are equal angles as there are corresponding angles.
\angle{AEB}=\angle{ADC} (corresponding angles)
\angle{ABE}=\angle{ACD} (corresponding angles)
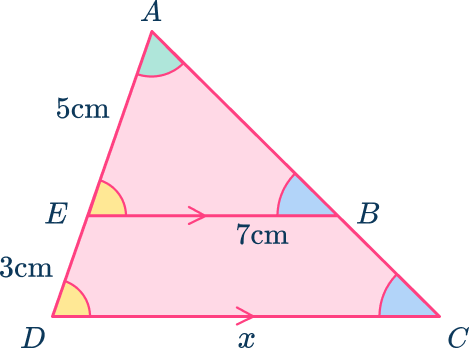
Redraw the triangles side by side.
Redraw the triangles side-by-side so that it is easier to pair up the corresponding sides.
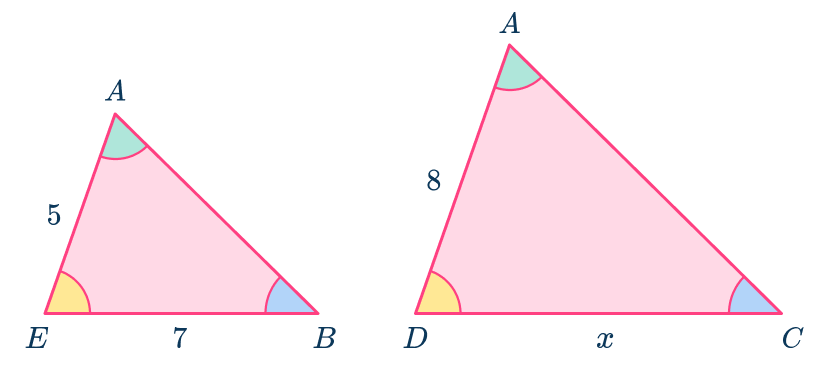
Decide which sides are pairs of corresponding sides.
Identify the corresponding sides that have measurements and those mentioned in the question. Use the angles to help you.
- The sides AE and AD are a pair of corresponding sides.
- The sides BE and CD are a pair of corresponding sides.
There are other corresponding sides, but you do not need them to answer the question.
Find the scale factor.
The ratio of the lengths AE\text{:}AD is 5\text{:}8 which simplifies to 1\text{:}\cfrac{8}{5} or 1\text{:}1.6.
The scale factor from ABE to ACD is 1.6 .
Use the scale factor to find the missing length.
The ratio of the lengths BE\text{:}CD is also 1\text{:}1.6.
Use the scale factor 1.6 as a multiplier to find the missing length.
The value of x has been found, x=11.2
Alternatively, an equation may be formed and solved:
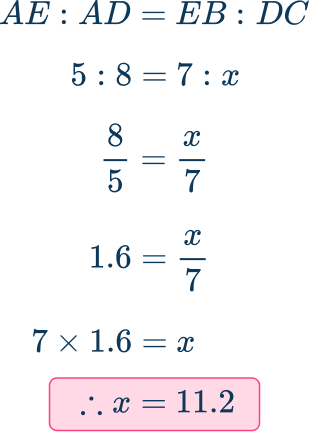
Teaching tips for similar shapes
- Introduce the topic with familiar, regular polygons, before progressing to more complex or irregular shapes.
- Use a variety of activities to teach students this topic, such as worksheets, interactive websites, or manipulatives. You can even challenge students to create similar shapes with given materials, having them justify their conclusions.
Easy mistakes to make
- Confusing the order of ratios
Make sure that you are consistent with your ratios. For example,
In this example, always write the A value first, and then the B value.
1\text{:}3 and 2\text{:}6. The ratios are equal, so these shapes are similar shapes.
- Using only what the shapes look like to decide if they are similar
Often diagrams for questions involving similar figures are NOT drawn to scale.
So, use the measurements given, rather than just looking or trying to measure on your own.
- Forgetting that shapes can be similar but in different orientations
The second shape may be in a different orientation to the first shape. The shapes can still be similar. For example, here shape A and Shape B are similar. Shape B is an enlargement of shape A by scale factor 2.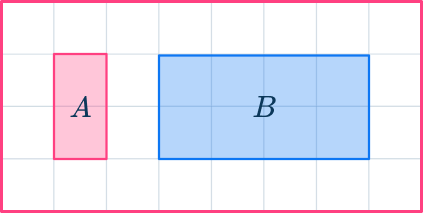
Here, shape B has been rotated to make the similarity easier to see.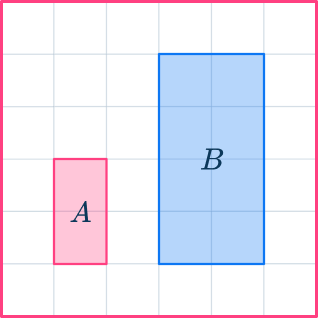
- Thinking scale factor is always a whole number
The scale factor can also be a fraction or a decimal. When the fraction or decimal is less than 1, it means the shape shrank.
Related congruence and similarity lessons
Practice similar shapes questions
1. Consider if these shapes are similar:
Yes – sides in ratio 1\text{:}4
No – sides in ratio 1\text{:}3 and 1\text{:}4
No – sides in ratio 1\text{:}3 and 1\text{:}2
Yes – sides in ratio 1\text{:}3
The shapes are similar, since the ratios of the corresponding sides are the same.
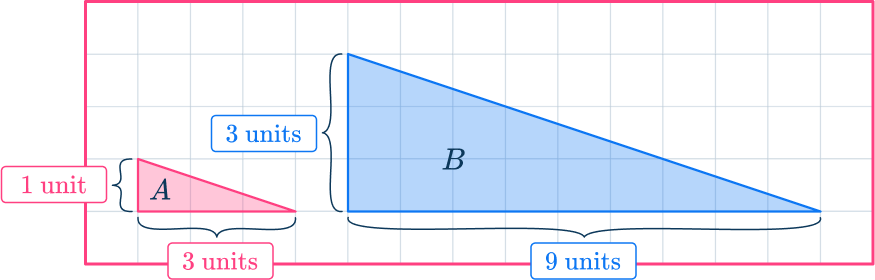
The ratio of the bases is \hspace{0.75cm} 3\text{:}9
which simplifies to \hspace{1.45cm} 1\text{:}3
and the ratio of the heights is \hspace{0.15cm} 1\text{:}3
2. Consider if these shapes are similar:
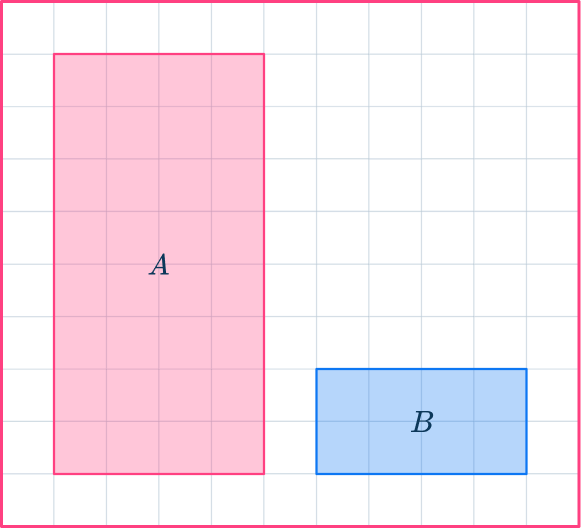
Yes – sides in ratio 2\text{:}1
Yes – sides in ratio 3\text{:}1
No – sides in ratio 2\text{:}1 and 1\text{:}2
No – sides in ratio 3\text{:}1 and 2\text{:}1
Comparing the base and height as shown creates the ratios 8\text{:}2 and 4\text{:}4, which are not equal.
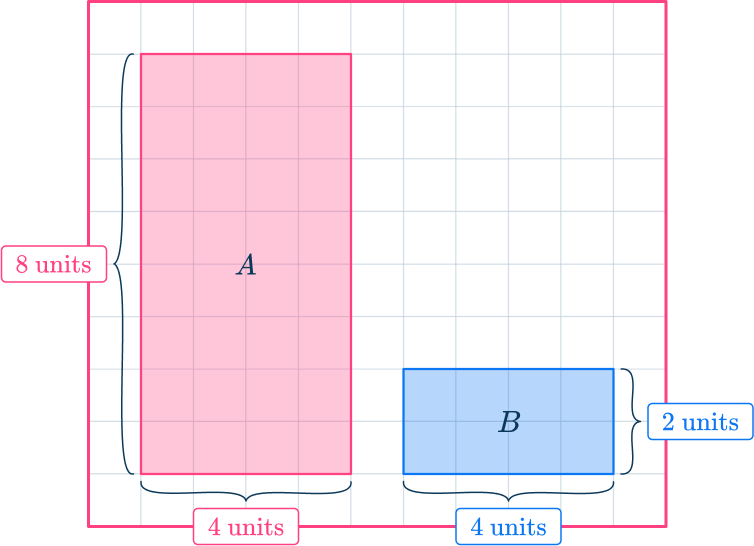
However if you rotate the shapes, they are similar since the ratios of the corresponding sides are the same.
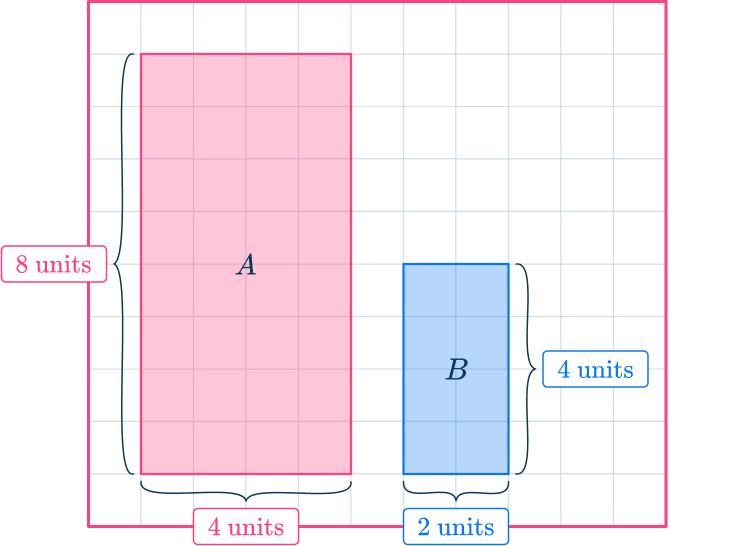
The ratio of the height is \hspace{0.65cm} 4\text{:}2
which simplifies to \hspace{1.45cm} 2\text{:}1
and the ratio of the base is \hspace{0.4cm} 8\text{:}4
which simplifies to \hspace{1.45cm} 2\text{:}1
3. These shapes are similar. Find the value of x.
The ratio of the bases is \hspace{0.75cm} 6\text{:}12
which simplifies to \hspace{1.45cm} 1\text{:}2
The scale factor from the red parallelogram to the blue is 2.
x=2 \times 5=10
4. These shapes are similar. Find the value of x.
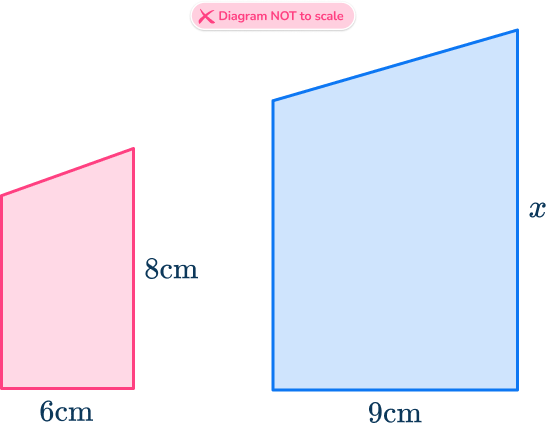
The ratio of the bases is \hspace{0.75cm} 6\text{:}9
which simplifies to \hspace{1.45cm} 1\text{:}\cfrac{9}{6}
or \hspace{3.65cm} 1\text{:}1.5
The scale factor from the small shape to the larger is 1.5.
x=8\times{1.5}=12
5. Find the value of x.
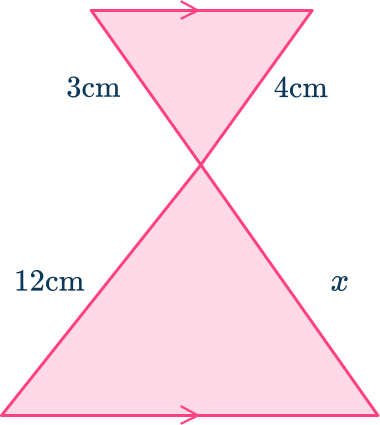
Use the parallel lines to identify equal angles.
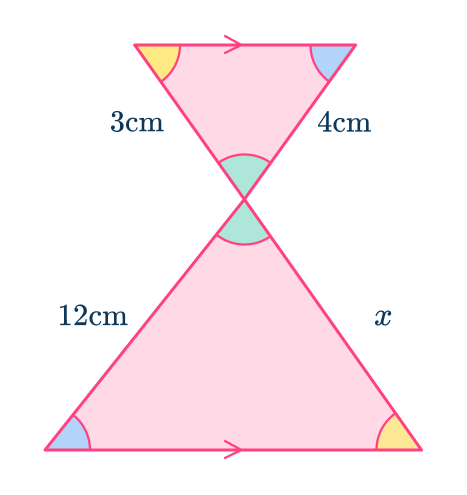
Then find pairs of corresponding sides.
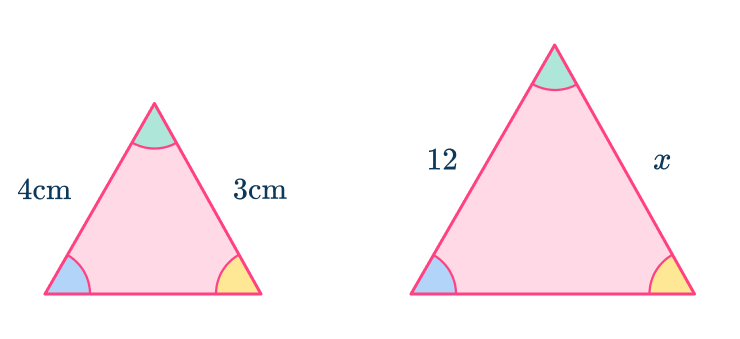
The ratio of the corresponding sides is 4\text{:}12, which simplifies to 1\text{:}3.
The scale factor from the smaller triangle to the larger is 3.
x=3\times{3}=9
6. Find the value of x.
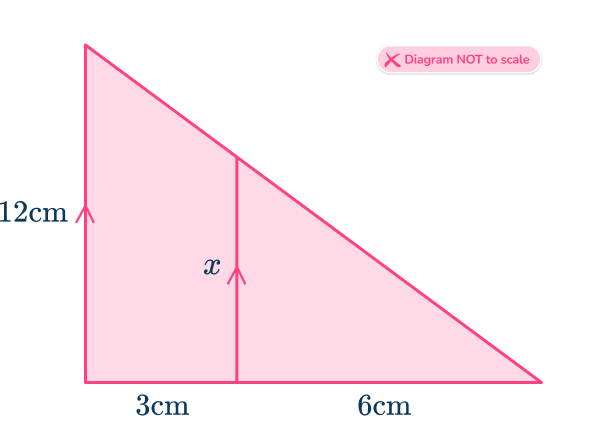
Use the parallel lines to identify equal angles.
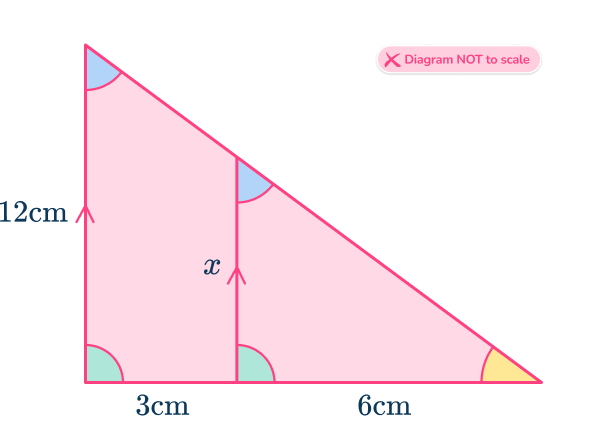
Then find pairs of corresponding sides.
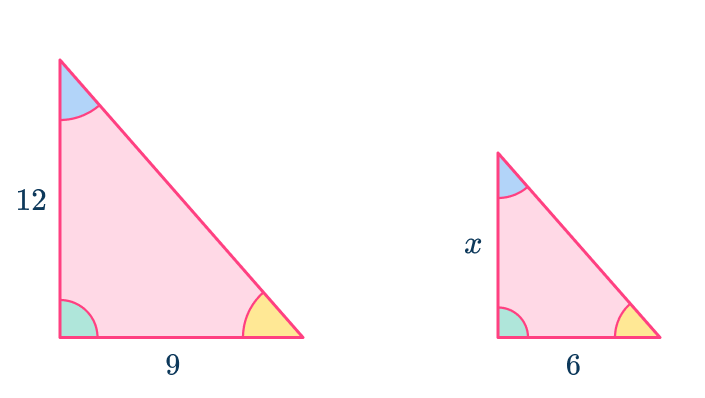
The ratio of the corresponding sides is 9\text{:}6, which simplifies to 1\text{:}23.
The scale factor from the larger triangle to the smaller is \cfrac{2}{3}.
x=12\times\cfrac{2}{3}=8
Similar shapes FAQs
Yes, similar shapes have different side lengths, but the ratio between corresponding side lengths is always equal.
A dilation is when a shape’s size is increased by a scale factor. A dilation creates a similar shape.
See also: Dilations
The theorem states that the sides of a right triangle are related by a^2+b^2=c^2, where a and b are the sides that form the right angle and c is the hypotenuse.
See also: Pythagorean Theorem
The next lessons are
- Transformations
- Mathematical proof
- Area
- Surface area
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!