[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
Rectangular prism
Here you will learn about rectangular prisms, including how to classify and identify rectangular prisms.
Students will first learn about rectangular prisms as a part of geometry in 1 st grade.
What is a rectangular prism?
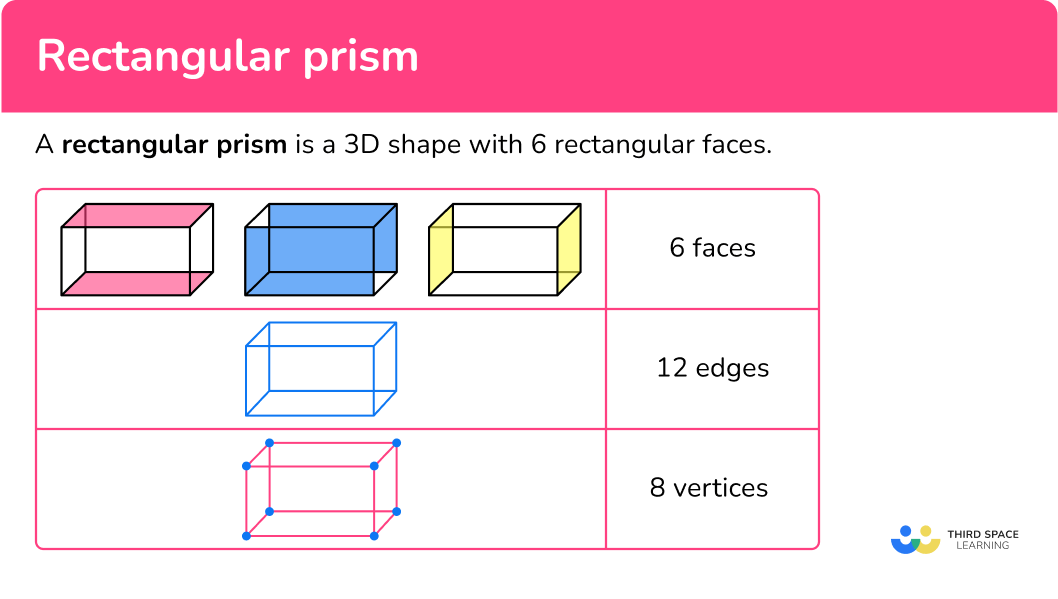
A rectangular prism is a three-dimensional shape, or 3D shape (polyhedron) with 6 rectangular faces that meet at right angles. They are also known as cuboids.
Cubes are a special type of rectangular prism where the length, width and height are all equal.
Examples of a rectangular prism:
Real life examples of rectangular prisms include shoe boxes, books and even the bricks on your house.
Properties of a rectangular prism
The properties of a rectangular prism include faces, edges, vertices (corners), length, width and height.
Faces
A face of a 3D shape is a flat surface.
Rectangular prisms have a total of \bf{6} faces – all of which are rectangular (or square).
Edges
An edge of a 3D shape is a straight line between two faces.
Rectangular prisms have \bf{12} edges:
Vertices
A vertex is a point where two or more edges meet.
Rectangular prisms have \bf{8} vertices:
Length, width and height
A rectangular prism has three dimensions: length, width, and height.
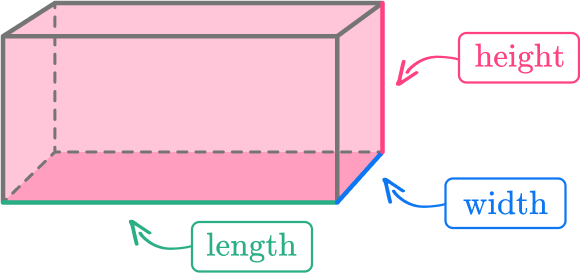
The length refers to the measurement from one end of the rectangular prism to the other, the width is the measurement from side to side, and the height of the rectangular prism is the measurement from top to bottom.
Labeling a rectangular prism
You can label the vertices (corners) of a rectangular prism to help us identify certain edges or faces.
For example,
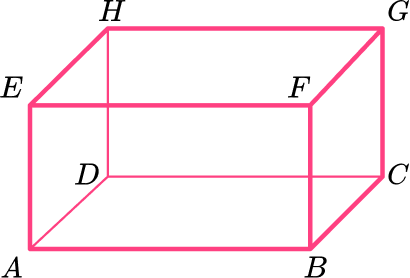
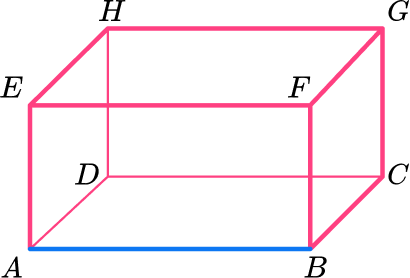
Using this labeling you can identify lengths, for example, the length AB :
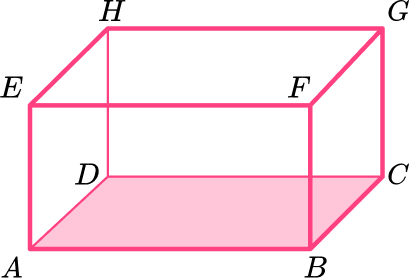
You can also identify faces, for example, the face ABCD :
What is a rectangular prism?
Common Core State Standards
How does this relate to 1 st grade math?
- Grade 1: Geometry (1.G.A.2)
Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.
![[FREE] 3D Shape Check for Understanding Quiz (Grade 1, 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/3D-Shape-listing-image.png)
[FREE] 3D Shape Check for Understanding Quiz (Grade 1, 5 and 6)
Use this quiz to check your grade 1, 5 and 6 students’ understanding of 3D shape. 10+ questions with answers covering a range of 1st, 5th and 6th grade 3D shape topics to identify areas of strength and support!
DOWNLOAD FREE [FREE] 3D Shape Check for Understanding Quiz (Grade 1, 5 and 6)
Use this quiz to check your grade 1, 5 and 6 students’ understanding of 3D shape. 10+ questions with answers covering a range of 1st, 5th and 6th grade 3D shape topics to identify areas of strength and support!
DOWNLOAD FREEHow to identify a rectangular prism
In order to identify a rectangular prism, you will:
- Look for the characteristics of a rectangular prism.
- State whether or not the shape is a rectangular prism.
- If the shape is not a rectangular prism, explain what characteristics are different.
Rectangular prism examples
Example 1: rectangular prism example
Look at the image below and determine if it is a rectangular prism or not.
- Look for the characteristics of a rectangular prism.
The shape has 4 triangular and 1 rectangular face, not 6 rectangular faces.
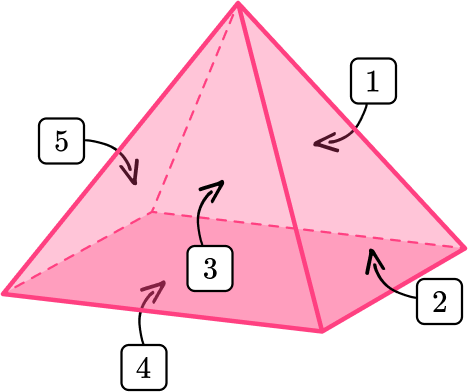
2State whether or not the shape is a rectangular prism.
This shape is not a rectangular prism, this shape is a pyramid.
3If the shape is not a rectangular prism, explain what characteristics are different.
This shape is not a rectangular prism because it has 4 triangular and 1 rectangular face.
Example 2: identify rectangular prisms
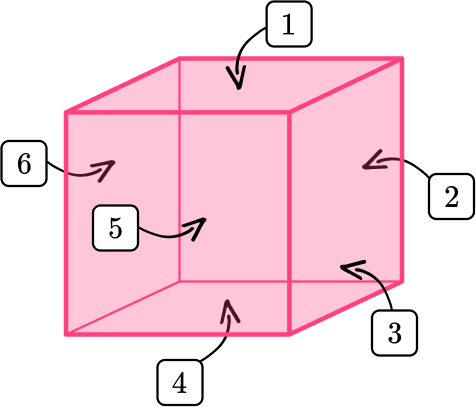
Look at the shape below and determine if it is a rectangular prism or not.
Look for the characteristics of a rectangular prism.
The shape has 6 square faces.
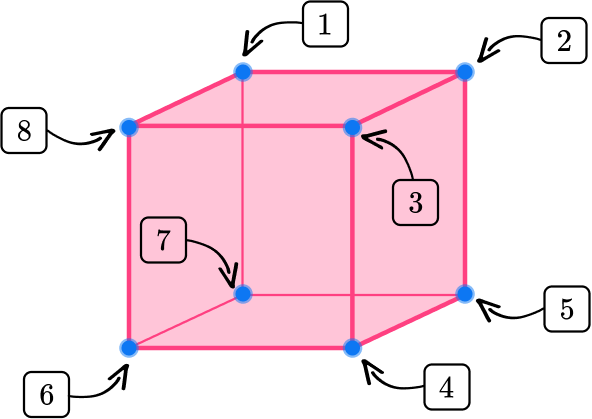
The shape has 8 vertices, or corners.
The shape has 12 edges.
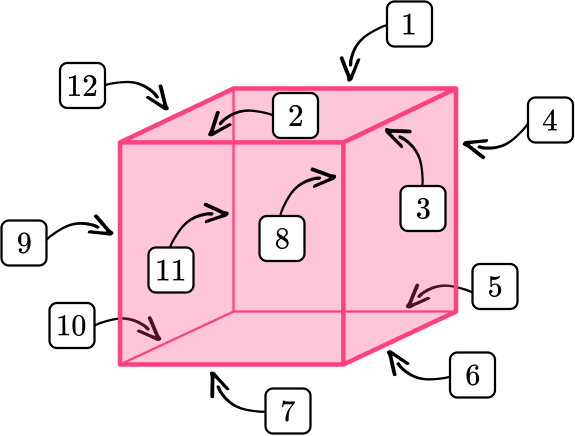
Are the side lengths different from each other?
No, all the sides are the same length.
State whether or not the shape is a rectangular prism.
This shape is a special kind of rectangular prism that has all equal sides. It is a cube.
Example 3: real-world example
Look at the image below and determine if it is a rectangular prism or not.
Look for and identify the characteristics of a rectangular prism.
The fish tank has 6 rectangular faces.
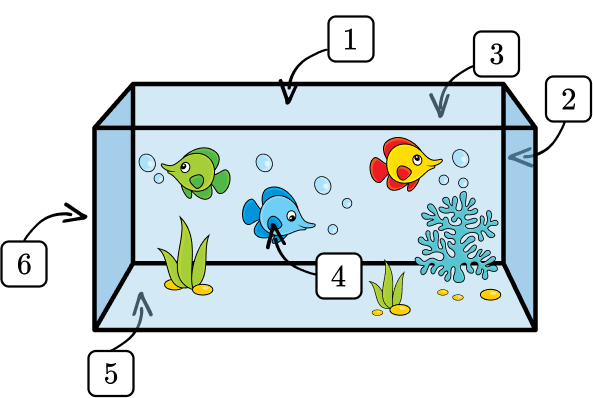
The fish tank has 8 vertices, or corners.
The fish tank has 12 edges.
Are the side lengths different from each other?
Yes, you can see that the sides on top and bottom are longer than the sides on the left and right.
State whether or not the shape is a rectangular prism.
The shape is a rectangular prism.
How to identify a rectangular prism in a 3D composite shape
In order to identify rectangular prisms in a composite shape, you will:
- Count the number of shapes that make up the composite shape.
- Identify and count the number of rectangular prisms within the shape.
- State the number of rectangular prisms within the composite shape.
Example 4: identify rectangular prisms within a 3D composite shape
Look at the composite shape and identify all rectangular prisms.
Count the number of shapes that make up the composite shape.
The composite shape is made up of 7 shapes.
Identify and count the number of rectangular prisms within the shape.
Each of these shapes has 6 regular faces that meet at right angles.
State the number of rectangular prisms within the composite shape.
The composite shape has 5 rectangular prisms: 3 cubes and 2 rectangular prisms.
Example 5: identify rectangular prisms within a 3D composite shape
Look at the composite shape and identify all rectangular prisms.
Count the number of shapes that make up the composite shape.
The composite shape is made up of 6 shapes.
Identify and count the number of rectangular prisms within the shape.
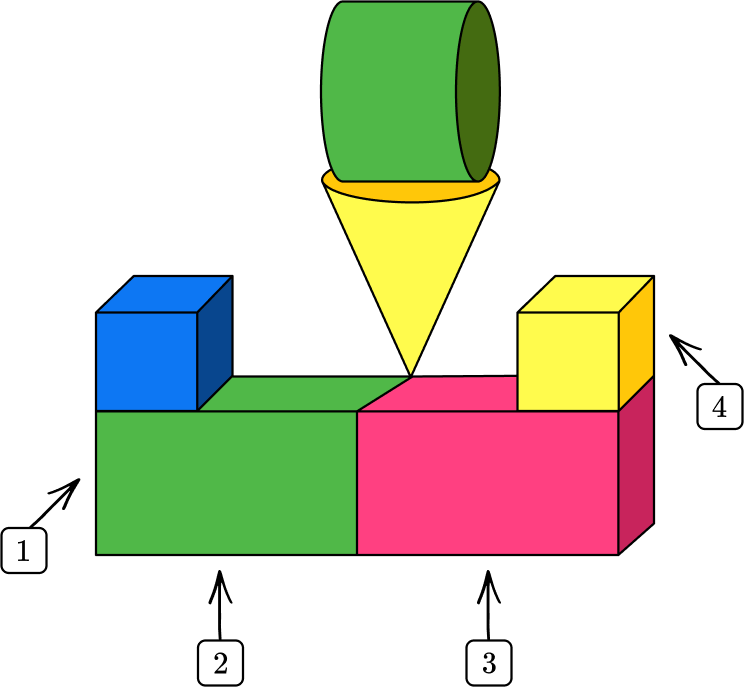
Each of these shapes has 6 regular faces that meet at right angles.
State the number of rectangular prisms within the composite shape.
The composite shape has 4 rectangular prisms: 2 cubes and 2 rectangular prisms.
Example 6: identify rectangular prisms within a 3D composite shape
Look at the composite shape and identify all rectangular prisms.
Count the number of shapes that make up the composite shape.
The composite shape is made up of 7 shapes.
Identify and count the number of rectangular prisms within the shape.
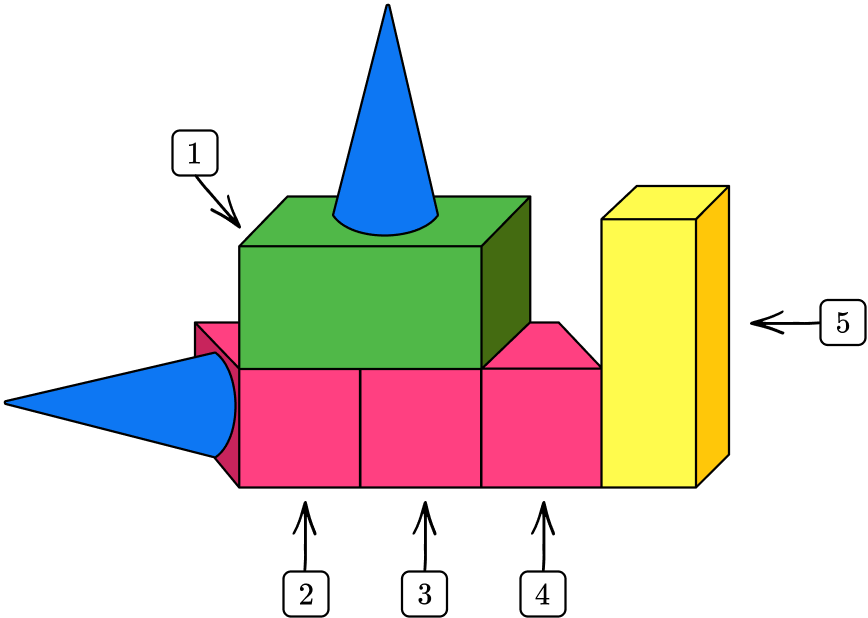
Each of these shapes has 6 regular faces that meet at right angles.
State the number of rectangular prisms within the composite shape.
The composite shape has 5 rectangular prisms.
Teaching tips for rectangular prisms
- Allow students the opportunity to explore and manipulate real-life examples of a rectangular prism. Some real-life examples of rectangular prisms are shoeboxes, books, refrigerators, and televisions. These objects have a box-like shape with rectangular sides.
- Provide students with physical rectangular prisms or building blocks to explore and manipulate. This hands-on approach helps them visualize and understand the properties and dimensions of rectangular prisms.
- With upper elementary students, in lue of working with rectangular prisms on worksheets, allow students to measure and compare the length, width, and height of rectangular prisms using rulers or measuring tapes. This helps reinforce the concept of dimensions and encourages critical thinking.
- Provide students with real-world practice problems or puzzles that involve rectangular prisms. For example, ask middle schoolers to calculate the volume or surface area of a rectangular prism or find the dimensions of an object given its properties.
- With students of all ages, draw connections between rectangular prisms and other geometric shapes, such as squares, rectangles, and cubes. Discuss similarities and differences in their properties to reinforce understanding.
Easy mistakes to make
- Assuming cubes are not rectangular prisms
Some definitions of rectangular prisms note that the sides are different lengths, meaning a cube could not be a rectangular prism. However, cubes are a special kind of rectangular prism, and should be considered one.
- Confusing edges and vertices
An edge is a line segment where two faces meet, while a vertex is a point where edges intersect.
- Confusing rectangles and rectangular prisms
Rectangles are 2D (they are made up of a length and width and are flat), and rectangular prisms are 3D (they are made up of rectangular faces and are not flat).
Related prism shape lessons
Practice rectangular prism questions
1. Which of the following is an example of a rectangular prism that is not a cube?
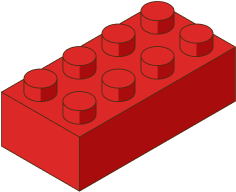
The building block is a rectangular prism. This shape has 6 rectangular faces, or sides, 8 vertices and 12 edges.
The soda can is a cylinder.
The ice cream cone is a cone.
The tissue box is a cube.
2. Which of the following is an example of a rectangular prism that is not a cube?
The ice cream sandwich is a rectangular prism. This shape has 6 rectangular faces, or sides, 8 vertices and 12 edges.
The soccer ball is a sphere.
The traffic cone is a cone.
The puzzle block is a cube.
3. Which of the following is an example of a rectangular prism that is not a cube?
The cereal box is a rectangular prism. This shape has 6 rectangular faces, or sides, 8 vertices and 12 edges.
The egg is an ellipsoid.
The party hat is a cone.
The dice is a cube.
4. How many rectangular prisms are in the composite shape below?
3
2
4
The composite shape is made up of 5 shapes.
3 of the 5 shapes are rectangular prisms, including the cube.
1 of the shapes is a cylinder and 1 is a cone.
5. How many rectangular prisms are in the composite shape below?
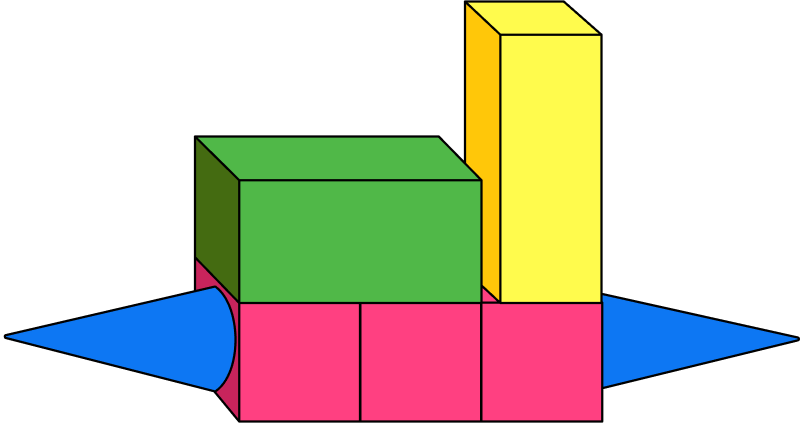
7
5
3
The composite shape is made up of 7 shapes.
5 of the 7 shapes are rectangular prisms.
The other two shapes are cones.
6. How many rectangular prisms are in the composite shape below?
1
2
5
The composite shape is made up of 5 shapes.
3 of the 5 shapes is a rectangular prism, including 2 cubes.
There is also 1 sphere and 1 cylinder in the shape.
Rectangular prism FAQs
A rectangular prism has different lengths, widths, and heights, while a cube has all sides of equal length.
No, parallelograms are two-dimensional shapes, whereas rectangular prisms are three-dimensional shapes.
See also: Parallelogram
Rectangular prisms are not the only type of prism you will encounter in your math career. As you progress through math, you will learn about other prisms including: hexagonal prisms, pentagonal prisms, and square prisms.
To find the volume of the rectangular prism, you multiply the length, width, and height of the prism together. The rectangular prism formula for volume is: \text{Volume} = \text{length} \times \text{width} \times \text{height} cubic units.
See also: Volume of a rectangular prism
To calculate the surface area of the rectangular prism, you add up the areas of all six faces. The rectangular prism formula is: \text{Surface Area} = 2 \, (length \times width + width \times height + height \times length).
See also: Surface area of a rectangular prism
To calculate the lateral surface area of a rectangular prism, you need to find the sum of the areas of all the rectangular faces excluding the top and bottom faces. Here’s the formula: \text{Lateral Surface Area} = 2 \times (length \times height + width \times height).
A rectangular prism has six faces, and all of them are rectangles. Opposite faces of a rectangular prism are congruent and parallel to each other. A triangular prism has two triangular bases and three rectangular faces connecting them. The shape of the faces and the arrangement of the angles differ between the two types of prisms.
It is another name for a rectangular prism – they mean the same thing.
The next lessons are
- Types of data
- Average and range
- Representing data
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!