High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
2D shapes Angles in polygons Types of angles Angles of a triangle Quadrilateral angles Pentagon shapePentagon angles
Here you will learn about angles in a pentagon, including finding the sum of the interior angles and solving problems involving interior angles and exterior angles.
Students will first learn about pentagon angles as part of geometry in 7 th grade.
What are pentagon angles?
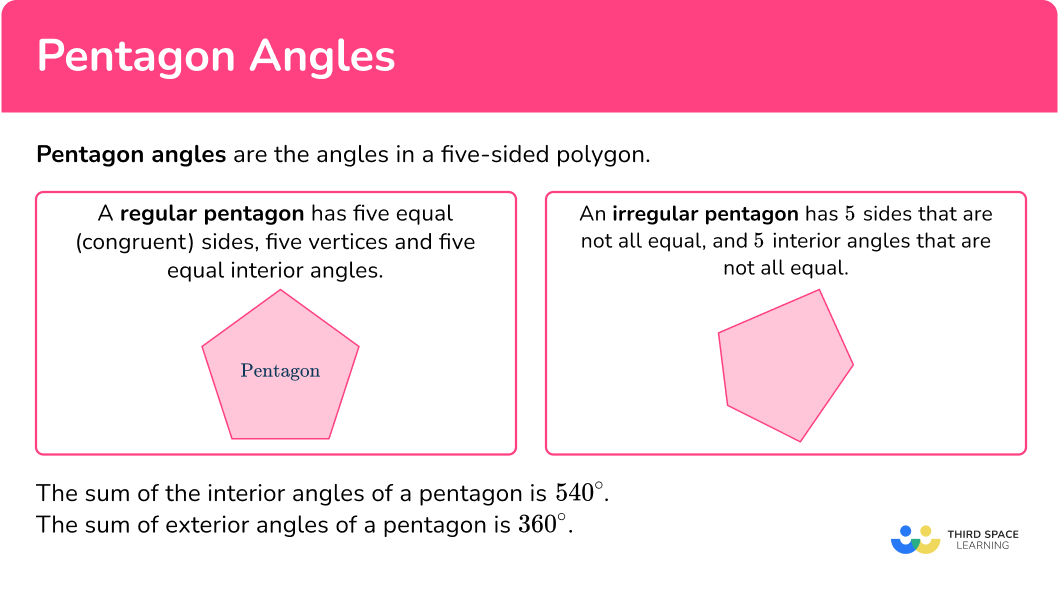
Pentagon angles are the angles in a five-sided polygon. In Greek, the prefix “penta” means “five” and the suffix “gon” means “angle.”
- Regular pentagons have five equal (congruent) sides, five vertices and five equal interior angles. You can refer to this as a convex pentagon because all of the angles are less than 180^{\circ}.

- An irregular pentagon has 5 sides that are not all equal, and 5 interior angles that are not all equal.

The sum of the interior angles of a pentagon is 540^{\circ}.
The sum of exterior angles of a pentagon is 360^{\circ}.
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Worksheet (Grade 4)
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Worksheet (Grade 4)
![[FREE] Angles Worksheet (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREEInterior and exterior angles of a pentagon
You need to be able to solve problems involving pentagon angles.
To do this you need to work with the interior and exterior angles of a pentagon.
A pair of interior and exterior angles of all polygons add to 180^{\circ} because they form a straight line. They are supplementary angles.
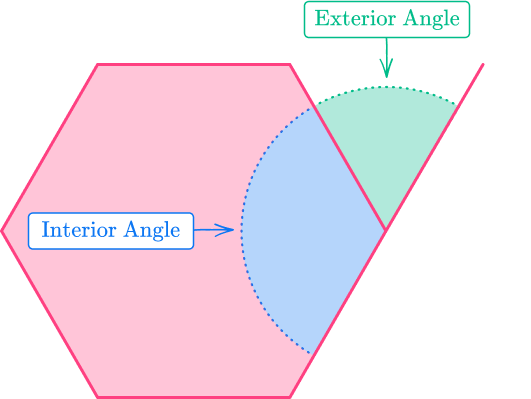
- The interior angles of a pentagon are the angles inside the 2D shape, formed when two sides of a pentagon meet.
You can find the sum of the interior angles of a polygon, including a pentagon, hexagon, or any other polygon using the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
A pentagon has 5 sides, so n=5
\text{ Sum of interior angles of a pentagon } =(5-2) \times 180
\begin{aligned} \hspace{2cm} & =3 \times 180 \\\\ & =540^{\circ} \end{aligned}
To find one interior angle of a regular pentagon, you can divide the sum of the interior angles by the number of sides, in this case, 5.
See also: Interior angles of a polygon
- Exterior angles of a pentagon are the angles between the pentagon and the extended line from the next side.
The sum of the exterior angles of any polygon is always 360^{\circ}.
To find each of the exterior angles of a regular pentagon, you can use the formula:
\text { Exterior angle of a regular polygon }=\cfrac{360}{n}, where n is the number of sides.
Alternatively, if you know the size of the exterior angle of a polygon, you can use a rearrangement of the above formula to identify the number of sides the polygon has.
\text { Number of sides }=\cfrac{360}{\text { exterior angle }}
See also: Sum of exterior angles of a polygon
What are pentagon angles?
Common Core State Standards
How does this relate to 7 th grade maths?
- Grade 7 – Geometry (7.G.B.5)
Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
How to solve problems involving pentagon angles
In order to solve problems involving pentagon angles:
- Identify if the pentagon is regular or irregular.
- Identify what the question is asking for.
- Solve the problem using the information you have gathered.
Pentagon angles examples
Example 1: finding the exterior angle of a regular pentagon
Below is a regular pentagon. Find the angle marked x.
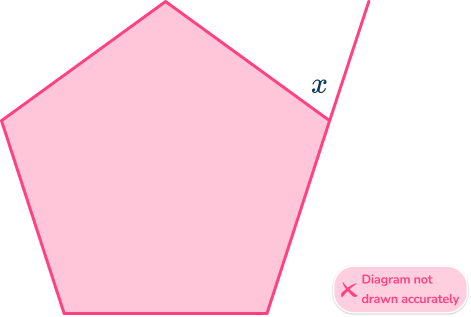
- Identify if the pentagon is regular or irregular.
The question tells us that this is a regular pentagon. This means the sides of the pentagon are equal and the interior angles are equal.
2Identify what the question is asking for.
The question wants us to find the angle x, which is one of the five exterior angles of this pentagon.
3Solve the problem using the information you have gathered.
To find the size of the exterior angles of a regular pentagon, you can use the formula:
\text { Exterior angle of a regular polygon }=\cfrac{360}{n}, where n is the number of sides.
So, the missing angle can be calculated as,
x=\cfrac{360}{5}=72^{\circ}.So, the exterior angle of a pentagon equals 72^{\circ}.
Example 2: finding the sum of the interior angles of a pentagon
What is the sum of the interior angles of a pentagon?
Identify if the pentagon is regular or irregular.
The question does not clarify whether the pentagon is regular or irregular, however, this doesn’t matter in the context of the question. The sum of the interior angles of a pentagon will be the same whether it is regular or irregular.
Identify what the question is asking for.
The question asks us to calculate the sum of the internal angles of a pentagon.
Solve the problem using the information you have gathered.
To calculate the sum of the interior angles of a pentagon, octagon or any polygon, you can use the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
Example 3: finding an interior angle of a regular pentagon
Below is a regular pentagon. Find the angle marked x.

Identify if the pentagon is regular or irregular.
The question tells us that this is a regular pentagon.
Identify what the question is asking for.
The question wants us to find the angle x, which is one of the five interior angles of this pentagon.
Solve the problem using the information you have gathered.
To find the size of the interior angle of any pentagon, you need to first calculate the sum of the interior angles.
To calculate the sum of the interior angles of any polygon, you can use the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can divide this by the number of sides, in this case 5, to find the size of one interior angle.
So, the missing angle can be calculated as:
x=\cfrac{540}{5}=108^{\circ}.
Hence, the missing angle measures 108^{\circ}.
Example 4: finding an interior angle of an irregular pentagon
Below is a polygon. Find the size of the missing angle x.
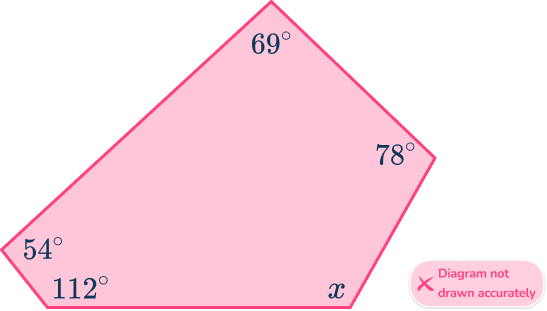
Identify if the pentagon is regular or irregular.
The question does not state whether the polygon is regular or irregular, however, the interior angles of the pentagon are not equal, so it must be irregular.
Identify what the question is asking for.
The question asks us to find the missing interior angle.
Solve the problem using the information you have gathered.
To find the size of an interior angle of any pentagon, you need first to calculate the sum of the interior angles.
To calculate the sum of the interior angles of any polygon, you can use the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can subtract the interior angles you know, to find the missing value.
x=540-(112+54+69+78)=227^{\circ}.
Example 5: finding an exterior angle of an irregular pentagon
Below is an irregular polygon. Find the size of the missing angle x.
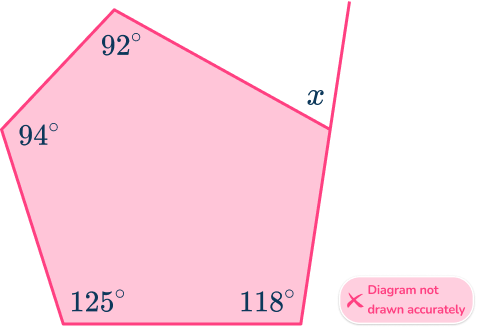
Identify if the pentagon is regular or irregular.
The question states that the polygon is irregular.
Identify what the question is asking for.
The question asks us to find the missing exterior angle.
Solve the problem using the information you have gathered.
To find the size of the exterior angle, x, you need to find the missing interior angle that corresponds to it, labeled y on the diagram below.
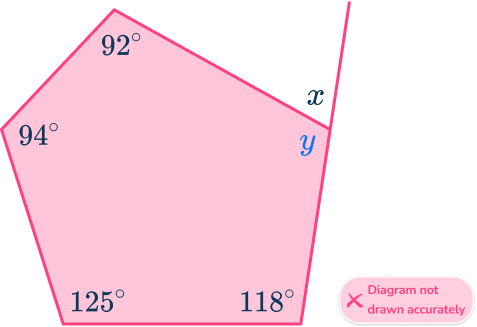
To find the size of an interior angle of any pentagon, you need to first calculate the sum of the interior angles.
To calculate the sum of the interior angles of any polygon, you can use the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can subtract the interior angles you know, to find the missing value.
x=540-(92+94+125+118)=111^{\circ}.
Now that you know the value of the interior angle corresponding to x, you can use the fact that the interior and exterior angles of all polygons add to 180^{\circ} because they form a straight line, to calculate the exterior angle.
So,
x=180-111=69^{\circ}.
Example 6: solving angle problems involving pentagons
The diagram shows a shape formed by two regular polygons.
Find the size of the angle labeled x.

Identify if the pentagon is regular or irregular.
The question states that both polygons in the diagram are regular polygons.
Identify what the question is asking for.
The question asks us to find the size of the angle x, which is formed on the exterior of the two regular pentagons.
Solve the problem using the information you have gathered.
To find the size of the angle, x, you need to find the missing interior angles that meet at the point.
To find the size of an interior angle of any pentagon, you need to first calculate the sum of the interior angles.
To calculate the sum of the interior angles of any polygon, you can use the formula:
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can divide this by the number of sides, in this case 5, to find the size of one of the interior angles.
So, the interior angles are
\cfrac{540}{5}=108^{\circ}.
Now that you know that the two interior angles are 108^{\circ} each, you can use the angle fact ‘angles around a point add up to 360^{\circ} to find the angle x.
So,
x=360-(108+108)=144^{\circ}.
Teaching tips for pentagon angles
- Provide worksheets with a variety of problems involving different types of pentagons, including finding missing angles in irregular pentagons and solving word problems.
- Discuss how changing the side lengths in irregular pentagons affects the angles.
- Suggested study materials include a handout showing the basic properties of polygons and the specific characteristics of pentagons as well as examples of pentagons in real life with corresponding angles and side lengths labeled.
Easy mistakes to make
- Not correctly identifying regular and irregular polygons
It is important to correctly identify whether a polygon is regular or irregular, using the information given in the question or on the diagram. Do not assume one or the other.
- Using the formulae incorrectly
Whether a polygon is regular or irregular will determine how the formulae for working with interior and exterior angles can be used. For example, the formula
\text { Exterior angle of a regular polygon }=\cfrac{360}{n}, where n is the number of sides, can only be used to find the size of exterior angles of regular polygons, where all exterior angles are equal.
Practice pentagon angles questions
1. Calculate the exterior angle of a regular pentagon.




You can find the size of an exterior angle of any regular polygon using the formula
\text { Exterior angle of a regular polygon }=\cfrac{360}{n}, where n is the number of sides.
So, the size of exterior angles of a regular pentagon can be calculated as \cfrac{360}{5}=72^{\circ}.
2. Calculate the sum of the interior angles of a 5 sided polygon.




You can find the sum of the interior angles of any polygon using the formula
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the sum of the interior angles of a pentagon can be calculated as
\begin{aligned}& =(n-2) \times 180 \\\\ & =(5-2) \times 180 \\\\ & =3 \times 180 \\\\ & =540^{\circ} \end{aligned}
3. The diagram shows a pentagon. Calculate the missing angle x.
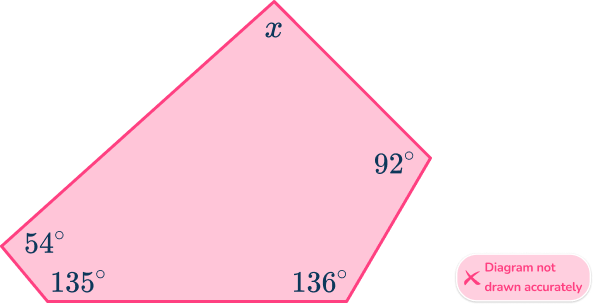




To find the value of one interior angle of an irregular polygon, you first need to calculate the sum of the interior angles of the polygon.
You can find the sum of the interior angles of any polygon using the formula
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the sum of the interior angles of a pentagon can be calculated as
\begin{aligned}& =(n-2) \times 180 \\\\ & =(5-2) \times 180 \\\\ & =3 \times 180 \\\\ & =540^{\circ} \end{aligned}
Now that you know the angles inside the pentagon add up to 540^{\circ}, you can subtract the interior angles you know, to find the missing value.
x=540-(54+92+135+136)=123^{\circ}.
4. The diagram shows a pentagon. Calculate the missing angle x.





The interior and exterior angles of any polygon add up to 180^{\circ}, so, x=180-64=116^{\circ}.
5. The diagram shows a pentagon. Calculate the missing angle x.
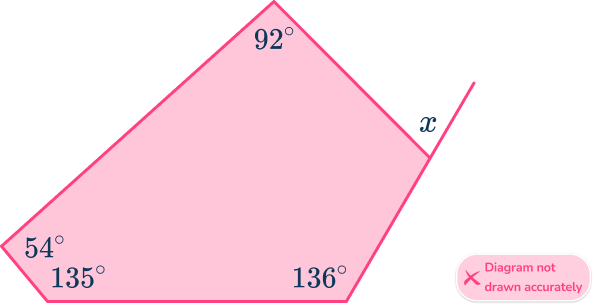




To find the size of the exterior angle, x, you need to find the missing interior angle that corresponds to it. To find the size of an interior angle of any pentagon you need to first calculate the sum of the interior angles.
To calculate the sum of the interior angles of any polygon you can use the formula
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
\begin{aligned}& =(n-2) \times 180 \\\\ & =(5-2) \times 180 \\\\ & =3 \times 180 \\\\ & =540^{\circ} \end{aligned}
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can subtract the interior angles you know, to find the missing value.
x=540-(92+54+135+136)=123^{\circ}.
Now that you know the value of the interior angle corresponding to x, you can use the fact that the interior and exterior angles of all polygons add to 180^{\circ} because they form a straight line, to calculate the exterior angle.
So,
x=180-123=57^{\circ}.
6. The diagram below is formed by three regular polygons. Find the size of the missing value x.





To find the size of the angle, x, you need to find the missing interior angles that meet it at the point.
To find the size of an interior angle of any pentagon you need to first calculate the sum of the interior angles
To calculate the sum of the interior angles of any polygon you can use the formula
\text { Sum of interior angles }=(n-2) \times 180, where n is the number of sides.
So, the interior angle of a pentagon can be calculated as
\begin{aligned}& =(n-2) \times 180 \\\\ & =(5-2) \times 180 \\\\ & =3 \times 180 \\\\ & =540^{\circ} \end{aligned}
Now that you know the angles inside a pentagon add up to 540^{\circ}, you can divide this by the number of sides, in this case 5, to find the size of one of the interior angles.
So, the interior angles are
\cfrac{540}{5}=108^{\circ}.
Now that you know that the three interior angles are 108^{\circ} each, you can use the angle fact ‘angles around a point add up to 360^{\circ} to find the angle x.
So,
x=360-(108+108+108)=36^{\circ}.
Pentagon angles FAQs
A pentagon is a type of polygon with 5 sides. In a regular pentagon, all interior angles are equal and measure 108 degrees. In an irregular pentagon, the angles can vary. The sum of the interior angles of any pentagon always adds up to 540 degrees.
A convex pentagon has all interior angles less than 180^{\circ} and no vertices pointing inward, while a concave pentagon has at least one interior angle greater than 180^{\circ} and at least one vertex pointing inward.
The polygon interior angle sum theorem states that the sum of the interior angles of a polygon with n sides is (n-2) \times 180^{\circ}.
The polygon exterior angle sum theorem states that the sum of the measures of the exterior angles of a polygon, one at each vertex, is always 360^{\circ}.
A pentagon has five sides. In a regular pentagon, all interior angles are 108 degrees. An irregular pentagon can have up to three right angles, as a fourth would leave no degree measure for the final angle, resulting in a straight line.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!