High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Parallel lines Perpendicular lines Types of anglesGeometry theorems
Here you will learn about geometry theorems, including the angle sum theorem, vertical angles theorem, alternate interior angles theorem, exterior angle theorem and the Pythagorean theorem.
Students will first learn about geometry theorems as part of geometry in 7 th and 8 th grade and continue to learn about them in high school.
What are geometry theorems?
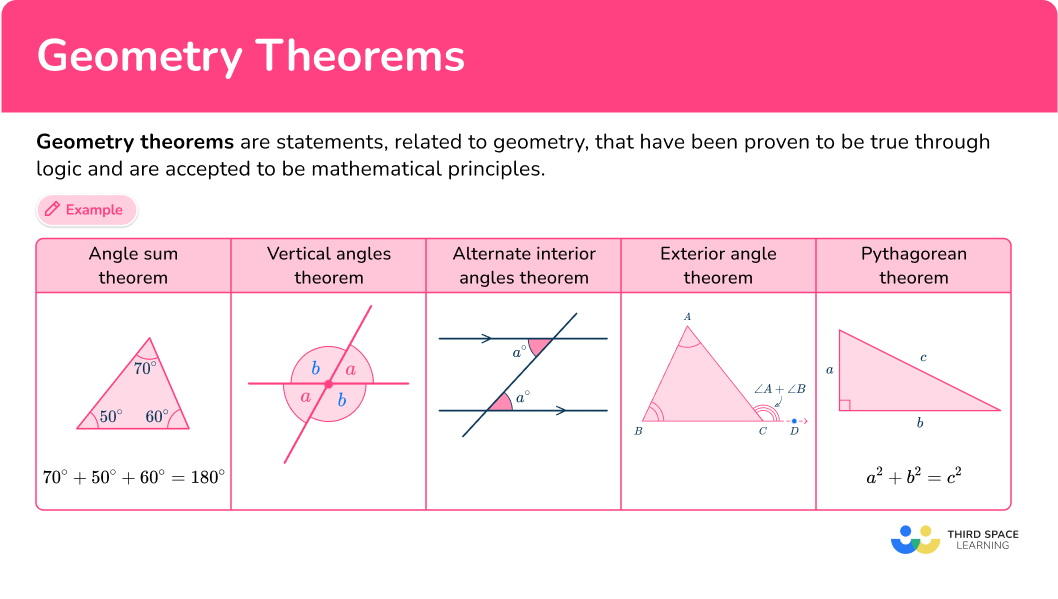
Geometry theorems are statements, related to geometry, that have been proven to be true through logic and are accepted to be mathematical principles.
Note: This page will overview geometry theorems and how to use them, but does not explore the proofs of these theorems.
The angle sum theorem (triangle sum theorem) says that the interior angles of any triangle will always have a sum of 180^{\circ}.
For example,
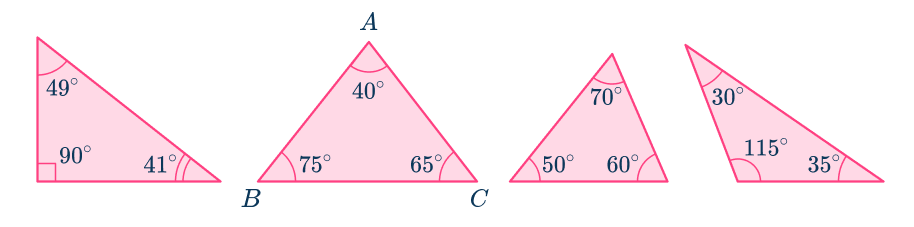
See also: Angles of a triangle
The vertical angles theorem (opposite angles) says when two lines intersect once they form two pairs of congruent angles.
For example,
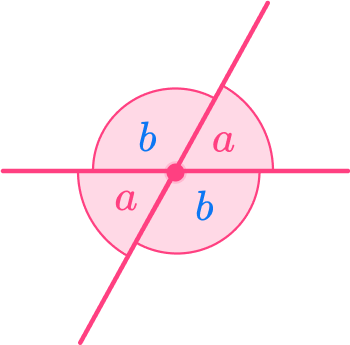
Step-by-step guide: Vertical angles theorem
The alternate interior angles theorem says when a transversal passes through two parallel lines, angles on opposite sides of the transversal, but inside the parallel lines are congruent (equal in measure).
For example,

See also: Alternate interior angles theorem
![[FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Check for Understanding Quiz (Grade 4)
![[FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
[FREE] Angles Check for Understanding Quiz (Grade 4)
![[FREE] Angles Check for Understanding Quiz (Grade 4)](https://thirdspacelearning.com/wp-content/uploads/2023/08/Angles-check-for-understanding-quiz-listing-image.png)
Use this quiz to check your grade 4 students’ understanding of angles. 10+ questions with answers covering a range of 4th grade angles topics to identify areas of strength and support!
DOWNLOAD FREEThe exterior angle theorem says the angle formed by extending a side of the triangle is equal to the sum of the other two non-adjacent angles in the triangle.
For example,
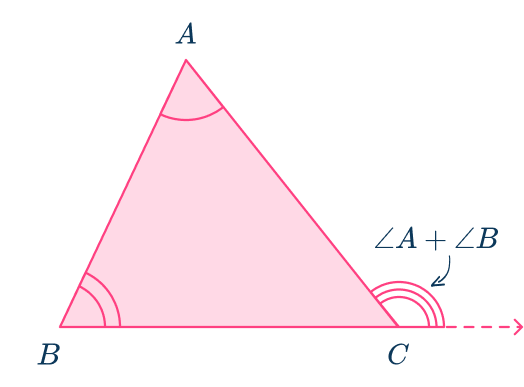
The Pythagorean theorem says the square of the hypotenuse of a right triangle (the longest side) is equal to the sum of the squares of the other two sides.
For example,
a^2+b^2=c^2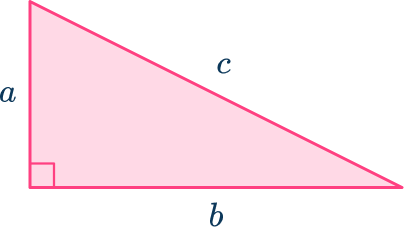
See also: Pythagorean theorem
What are geometry theorems?
Common Core State Standards
How does this relate to 7 th grade math and 8 th grade math?
- Grade 7 – Geometry (7.G.B.5)
Use facts about supplementary, complementary, vertical, and adjacent angles in a multi-step problem to write and solve simple equations for an unknown angle in a figure.
- Grade 8 – Geometry (8.G.A.5)
Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.
- Grade 8 – Geometry (8.G.B.6)
Explain a proof of the Pythagorean Theorem and its converse.
- Grade 8 – Geometry (8.G.B.7)
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
How to use geometry theorems to solve problems
In order to use geometry theorems to solve problems:
- Decide which theorem is needed to solve.
- Use the theorem to solve.
Geometry theorem examples
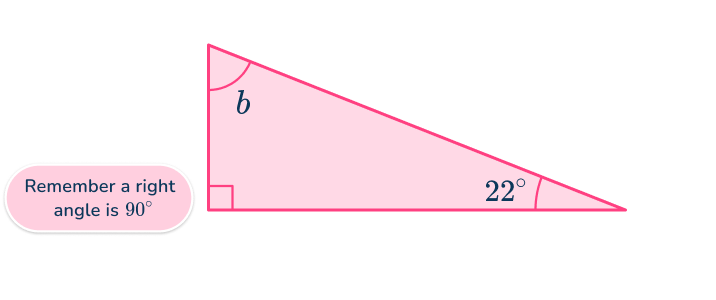
Example 1: missing angle in a triangle
Find the measure of the unknown angle labeled b in the following triangle:
- Decide which theorem is needed to solve.
The question is asking about the total measurement of the interior angles of a triangle. This is the angles sum theorem.
2Use the theorem to solve.
The angles sum theorem says that all interior angles of a triangle sum to be 180^{\circ}.
Add up the angles that are given within the triangle.The angles 90^{\circ} and 22^{\circ} are given. Add these together:
90+22=112^{\circ}Subtract 112^{\circ} from 180^{\circ}\text{:}
b=180-122=68^{\circ}Example 2: missing angles in intersecting lines
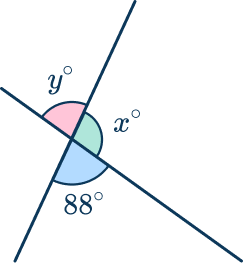
Find the values of angles x and y.
Decide which theorem is needed to solve.
The question is asking about the angles formed by two intersecting lines. This is the vertical angles theorem.
Use the theorem to solve.
The angle labeled y and the angle with value 88^{\circ} are vertical angles, since their vertex is created by two straight lines intersecting.
y=88^{\circ} because vertical angles are congruent (theorem 1 ).
x and y are not vertical angles, but they are supplementary angles because they are on a straight line at the same vertex. Supplementary angles have a sum of 180^{\circ} (theorem 2 ).
\begin{aligned}& x+y=180 \\\\
& x+88=180 \\\\
& x=92^{\circ} \end{aligned}
x=92^{\circ}, y=88^{\circ}
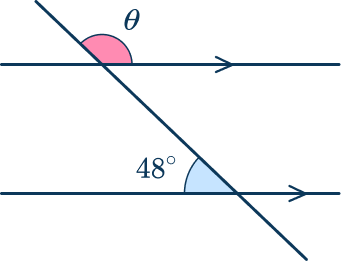
Example 3: missing angle in a parallel lines cut by a transversal
Calculate the size of the missing angle \theta. Justify your answer.
Decide which theorem is needed to solve.
The question is asking about the angles formed by a transversal cutting through two parallel lines. This is the alternate interior angles theorem.
Use the theorem to solve.
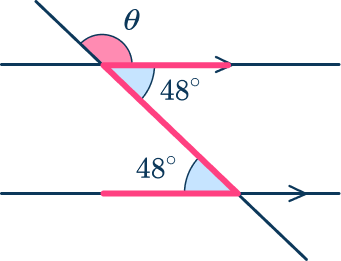
Here you can label the alternate angle on the diagram as 48^{\circ}.
Use basic angle facts to calculate the other missing angle.
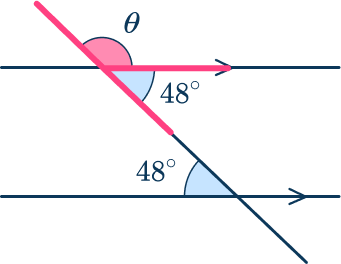
Here as \theta is on a straight line with 48^{\circ},
\theta=180-48=132^{\circ}
Example 4: missing exterior angle in a triangle
Calculate the value of x.
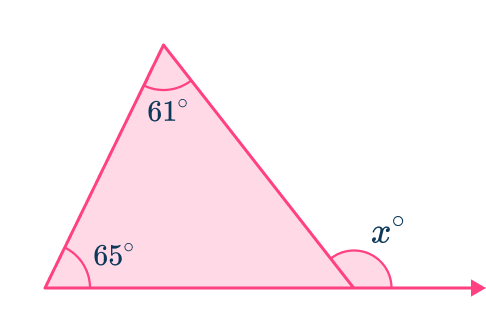
Decide which theorem is needed to solve.
The question is asking about the angles formed by a line extending from the base of a triangle. This is the exterior angle theorem.
Use the theorem to solve.
The exterior angle theorem says that the measure of the exterior angle of a triangle is the sum of the two non-adjacent interior angles of the triangle.
In this case, x=65+61=126^{\circ}
Example 5: missing exterior angle in a triangle
Calculate the value of x.
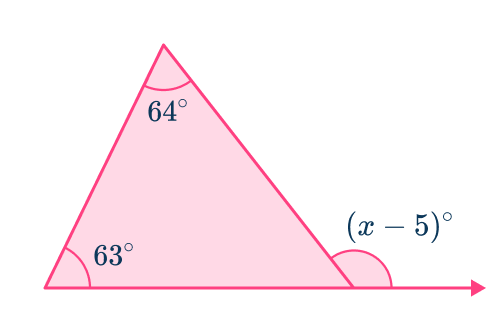
Decide which theorem is needed to solve.
The question is asking about the angles formed by a line extending from the base of a triangle. This is the exterior angle theorem.
Use the theorem to solve.
The exterior angle theorem says that the measure of the exterior angle of a triangle is the sum of the two non-adjacent interior angles of the triangle.
In this case, x-5=63+64, so x=132 and the exterior angle measures 127^{\circ}.
Example 6: missing length of the hypotenuse c
Find the third side, x, and answer to the nearest hundredth.
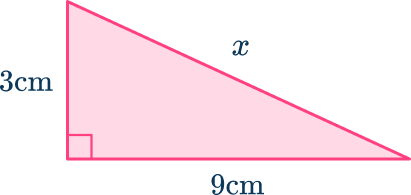
Decide which theorem is needed to solve.
The question is asking about the side lengths of a right triangle. This is the Pythagorean theorem.
Use the theorem to solve.
Label the hypotenuse (the longest side) with c. The adjacent sides, next to the right angle can be labeled a and b (either way – they are interchangeable).
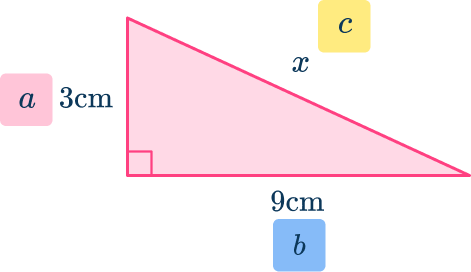
Write down the formula and apply the numbers.
\begin{aligned}& a^2+b^2=c^2 \\\\
& 3^2+9^2=x^2 \\\\
& 9+81=x^2 \\\\
& 90=x^2 \\\\
& \sqrt{90}=x \end{aligned}
An alternative method of rearranging the formula and to put one calculation into a calculator will also work.
\begin{aligned}& a^2+b^2=c^2 \\\\
& c^2=a^2+b^2 \\\\
& c=\sqrt{a^2+b^2} \\\\
& x=\sqrt{3^2+9^2} \end{aligned}
Make sure you give your final answer in the correct form by calculating the square root value; including units where appropriate.
x=\sqrt{90}=9.48683298 \ldots
The final answer to the nearest hundredth is:
x=9.49 \mathrm{~cm}
Teaching tips for geometry theorems
- Introduce all geometric theorems with whole numbers, such as whole number sides of a triangle or angle measurements, so that students can focus on the qualities of the theorem and not the calculations.
- Once students understand all the theorems, challenge them to prove angle congruence using a mixture of the theorems.
Easy mistakes to make
- Incorrectly labeling angles
Write neatly, so that you can keep track of each angle measurement and avoid mistakes.
- Assuming corresponding sides or angles are equal, because they “look” equal
It is important to remember that the images are not to scale, so just because an angle “looks” like a certain measurement, does not make it true. Always use only the information given to solve, instead of measuring with a ruler endpoint to endpoint or using a protractor.
- Mixing up the terminology for the theorems
This is particularly common with theorems that have similar names. There are different rules for the same-side interior angles theorem, than the alternate interior angles theorem. Always pay close attention to the theorem name and the angles given in a problem.
Practice geometry theorem questions
1. Find the measure of the angle c\text{:}
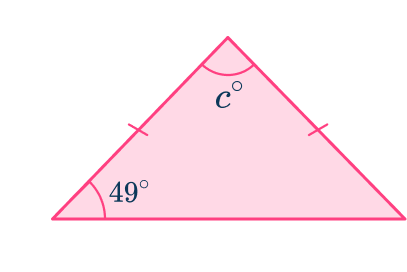




This is an isosceles triangle and the two angles at the bottom of the triangle are equal.
\begin{aligned}& 49+49=98 \\\\ & 180-98=82^{\circ} \end{aligned}
2. Find the value of the angle labeled x and y.
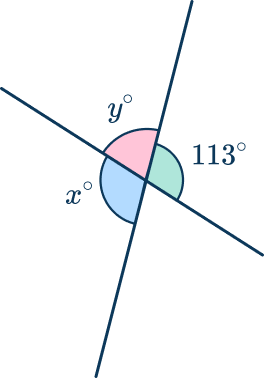




Angle x is vertically opposite the given angle 113^{\circ}, so it is the same.
x=113^{\circ}
Angle x and angle y lie on a straight line, so they must add up to 180^{\circ}.
\begin{aligned}& 113+y=180 \\\\ & y=67^{\circ} \end{aligned}
3. What is the measure of angle m?
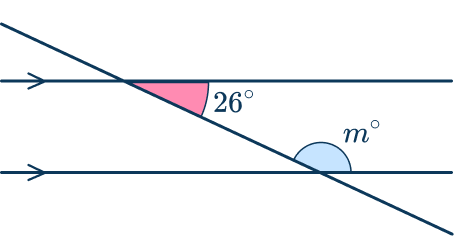




The two parallel lines are cut by a transversal, creating alternate interior angles that are congruent.
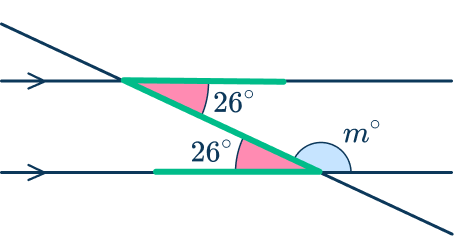
The new 26^{\circ} angle and m are supplementary angles, so their sum is 180^{\circ}.
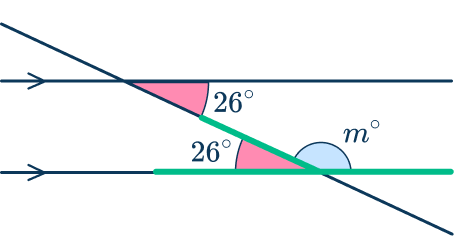
\begin{aligned}&26+m=180 \\\\ &180-26=m \\\\ &m=154^{\circ} \end{aligned}
4. Calculate the value of x.





The exterior angle theorem says that the angle formed by extending a side of the triangle is equal to the sum of the other two non-adjacent angles in the triangle.
This means that angle x is equal to the sum of 37^{\circ} and 89^{\circ}.
So,
x=37+89=126^{\circ}
5. Calculate the value of x.
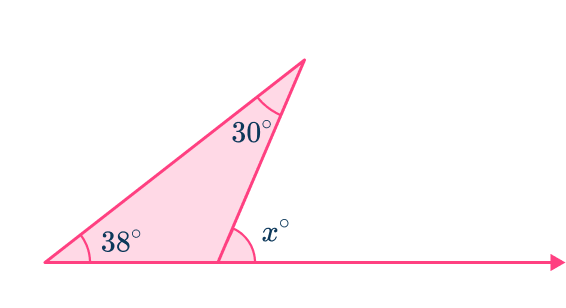




The exterior angle theorem says that the angle formed by extending a side of the triangle is equal to the sum of the other two non-adjacent angles in the triangle.
This means that angle x is equal to the sum of 38^{\circ} and 30^{\circ}.
So,
x=38+30=68^{\circ}
6. Find side x. Give your answer to the nearest hundredth:





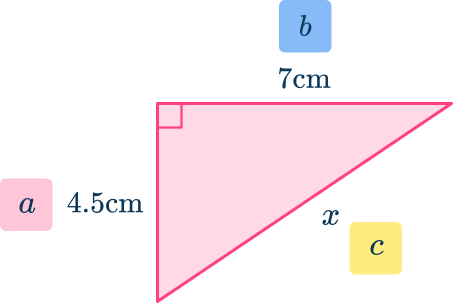
\begin{aligned}&a^2+b^2=c^2 \\\\ &7^2+4.5^2=x^2 \\\\ &x^2=7^2+4.5^2 \\\\ &x^2=49+20.25 \\\\ &x^2=69.25 \\\\ &x=\sqrt{69.25} \\\\ &x=8.32165849 \ldots… \end{aligned}
x=8.32 \mathrm{~cm}
Geometry theorems FAQs
A postulate is accepted as true without proof (assumed to be true), but a theorem requires proof (proven to be true).
Angle pairs formed when a transversal intersects two parallel lines.
See-also: Corresponding angles
The point in the middle of a line segment.
A line, line segment, or ray that divides an angle into two equal angles. For example, the diagonals of a parallelogram bisect each other.
A four sided polygon (quadrilateral), with two pairs of parallel opposite sides and opposite equal angles.
For example,
Shape ABCD is a parallelogram and \angle{ABC}=\angle{ADC}. 
The next lessons are
- Parallel angles
- 2D shapes
- Triangles
- Directly proportional graph
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!