High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Fractions Decimals 2D shapes Quadrilateral Coordinate planeDilations
Here you will learn about dilations, including how to enlarge a 2D shape by a scale factor and how to describe dilation geometry in detail.
Students will first learn about dilations as part of geometry in 8 th grade.
What are dilations?
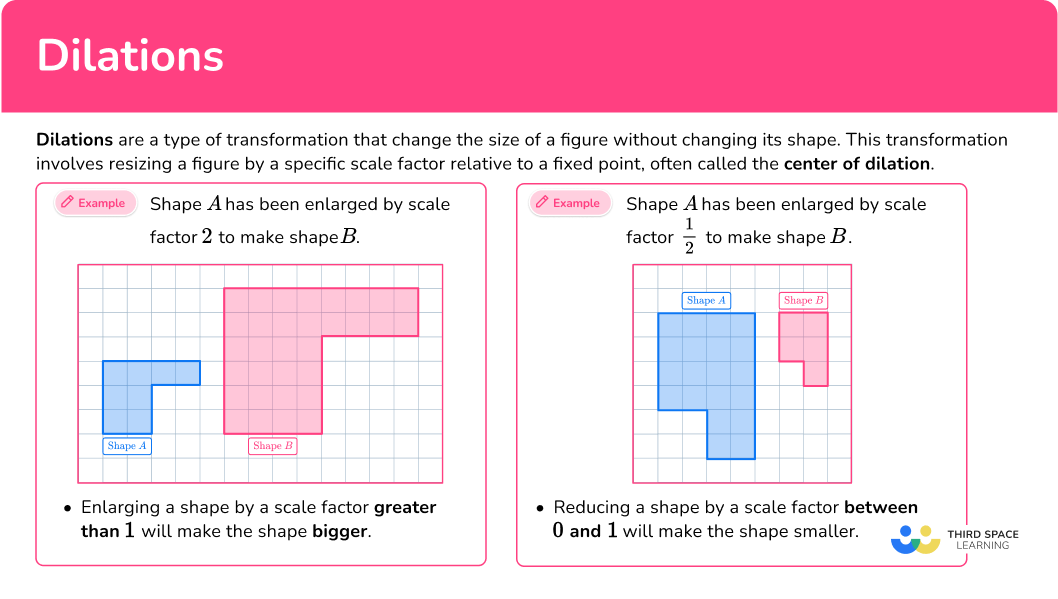
Dilations are a type of transformation that change the size of a figure without changing its shape. This transformation involves resizing a figure by a specific scale factor relative to a fixed point, often called the center of dilation.
Dilations have real life functions, such as changing the size of photographic prints or pictures in documents.
- Enlarging a shape by a scale factor greater than \bf{1} will make the shape bigger.
For example,
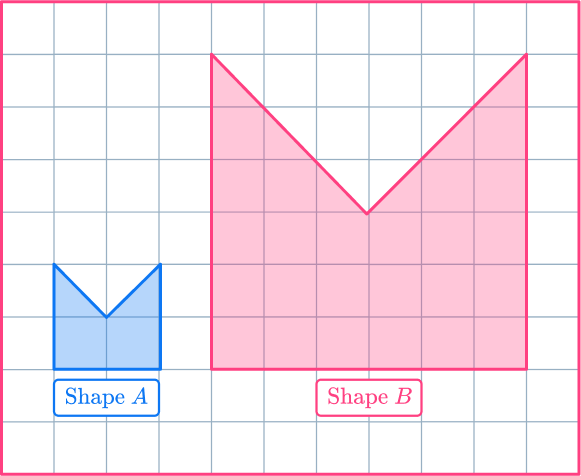
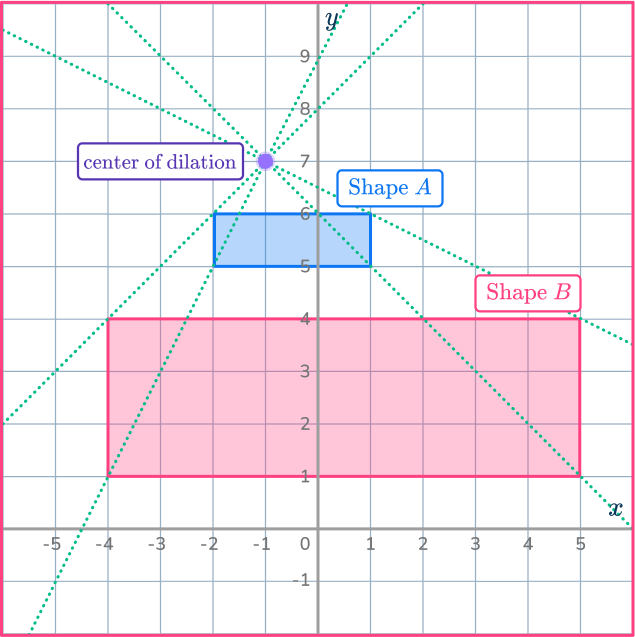
Shape A has been enlarged by scale factor 2 to make shape B.
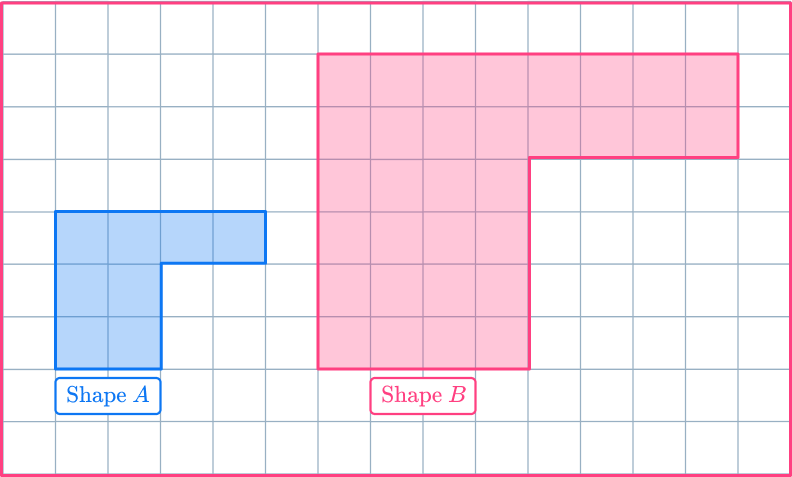
The corresponding angles are identical, but the length of each side in shape B is double the size of the original shape.
You need to multiply the original lengths by the scale factor to find the lengths of the enlarged shape.
- Reducing a shape by a scale factor between \bf{0} and \bf{1} will make the shape smaller. This is often written as a fraction and is known as a fractional scale factor.
For example,
Shape A has been reduced by scale factor \cfrac{1}{2} to make shape B.
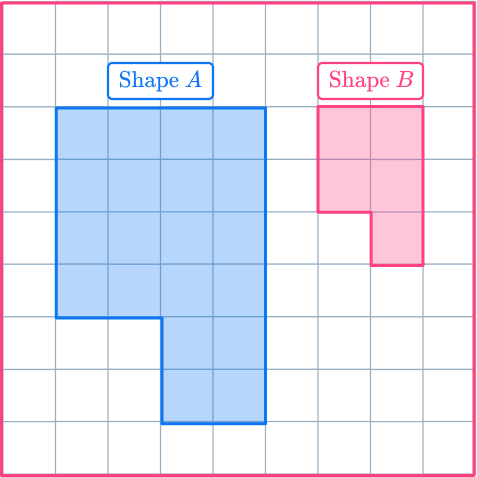
The corresponding angles are identical, but the length of each side in shape B is half the size of the original shape.
The object is the name of the original shape.
The image (or dilation image) is the name of the shape after it has been translated.
When an object is enlarged or reduced, the object and the image are similar shapes.
Step-by-step guide: Scale factor
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREE![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREECenter of dilation
The center of dilation places the enlargement or reduction in a specific place.
To use a center of dilation, you need to draw straight lines from the center of dilation through the vertices of the original shape. These are called ray lines.
For example, here triangle ABC has been enlarged by scale factor 2 about a center of dilation point O. The new triangle is labelled A’B’C’.
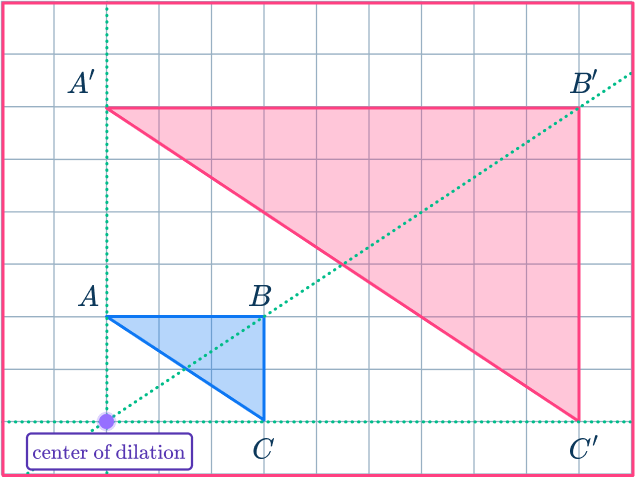
The lengths of the sides of the new triangle are double the lengths of the sides of the original triangle.
The pairs of corresponding sides are parallel lines.
The angles in the two shapes are the same.
The triangles are similar triangles.
Step-by-step guide: Center of dilation
What are dilations?
Common Core State Standards
How does this relate to 8 th grade math and high school math?
- Grade 8 – Geometry (8.G.A.3)
Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.A.1a)
A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged.
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.A.1b)
The dilation of a line segment is longer or shorter in the ratio given by the scale factor.
How to solve problems involving dilations
In order to solve problems involving dilations:
- Understand the problem.
- Apply the dilation transformation or solve for the desired information.
Dilations examples
Example 1: use a scale factor to enlarge a shape
Enlarge the shaded shape by scale factor 2.
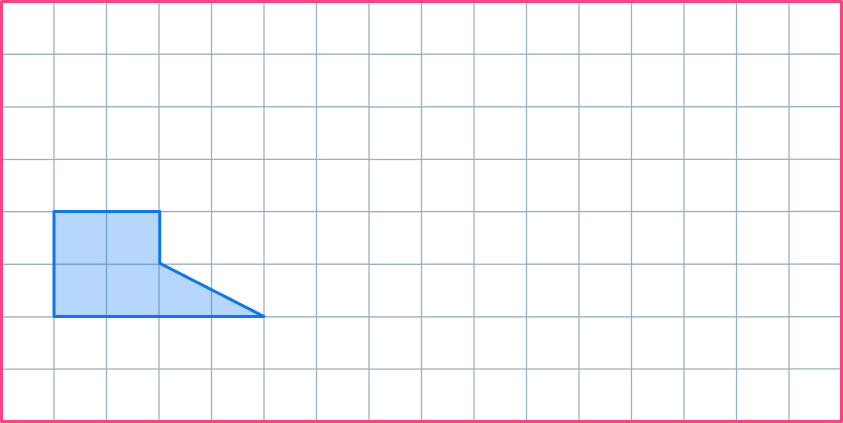
- Understand the problem.
The problem is asking you to draw a second shape as an enlargement of the original shape given using a scale factor of 2.
2Apply the dilation transformation or solve for the desired information.
You can apply the dilation transformation here by multiplying the original lengths by the scale factor to find the lengths of the enlarged shape. It is easier to start with horizontal or vertical lines.
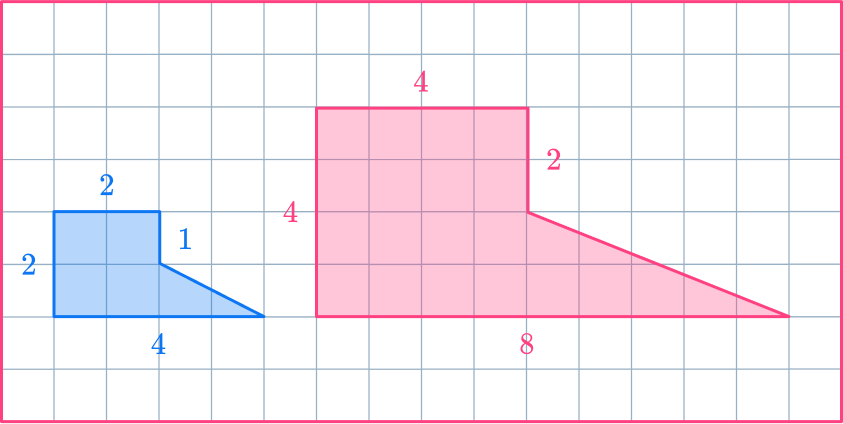
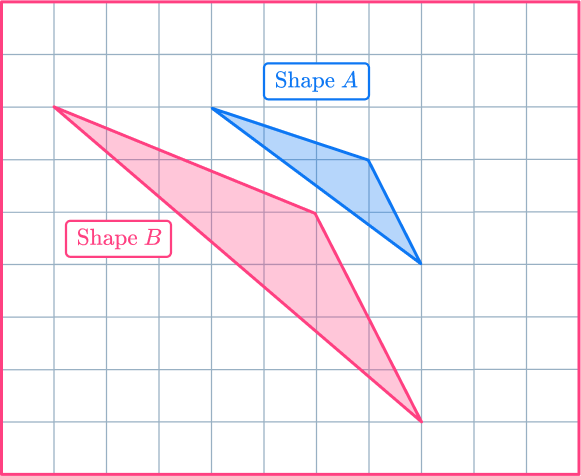
Example 2: calculating a scale factor
Shape A has been enlarged to make shape B. Calculate the scale factor.
Understand the problem.
Here, you are given both the original shape and the dilation image and need to compare the side lengths to find the scale factor.
Apply the dilation transformation or solve for the desired information.
To calculate the scale factor, you need to divide an enlarged length by the corresponding original length.
scale \, factor = \cfrac{enlarged \, length}{ original \, length}=\cfrac{6}{2}=3
Example 3: with a center of dilation on a grid
Enlarge the shaded shape with scale factor 3 about the center of dilation.
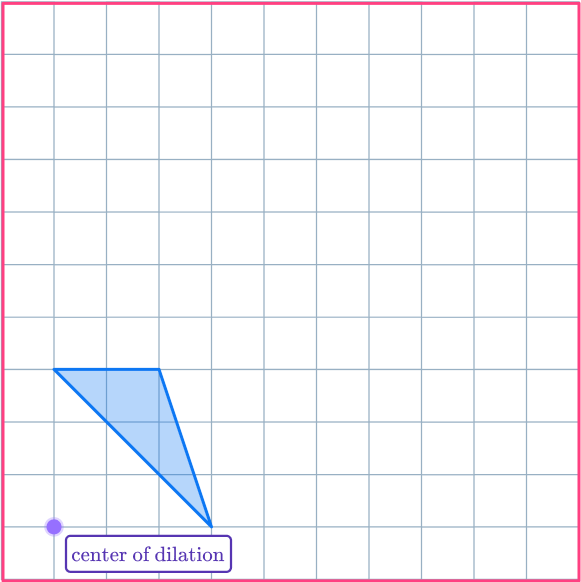
Understand the problem.
Here, you must draw a dilation image using a scale factor of 3. This means each side length of the dilation image will be 3 times as long as the corresponding side length of the original shape.
To use a center of dilation, you need to draw ray lines from the center of dilation through the vertices of the original shape.
Apply the dilation transformation or solve for the desired information.
Use the ray lines to help you enlarge the shape.
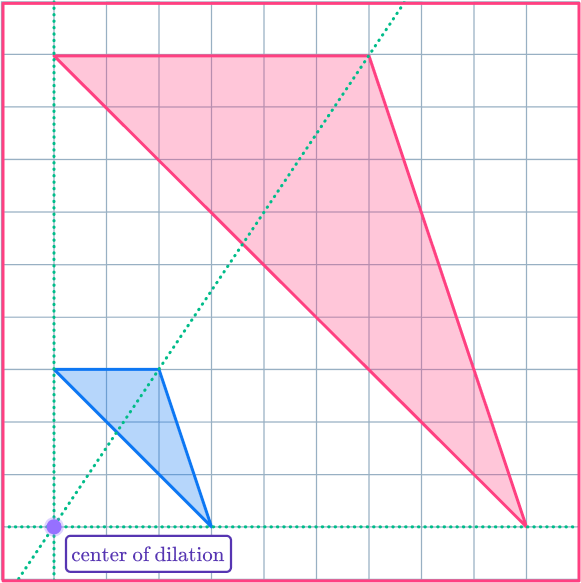
Example 4: with a center of dilation on a coordinate plane
Enlarge the shaded shape by scale factor 2 about the point (1,2) .
Understand the problem.
Here, you must draw a dilation image using a scale factor of 2. This means each side length of the dilation image will be 2 times as long as the corresponding side length of the original shape.
To use a center of dilation, you need to draw ray lines from the center of dilation through the vertices of the original shape.
Apply the dilation transformation or solve for the desired information.
First, you’ll need to plot the center of dilation on the coordinate grid. Then draw ray lines from the center of dilation through the vertices of the original shape. Use the ray lines to help you enlarge the shape.
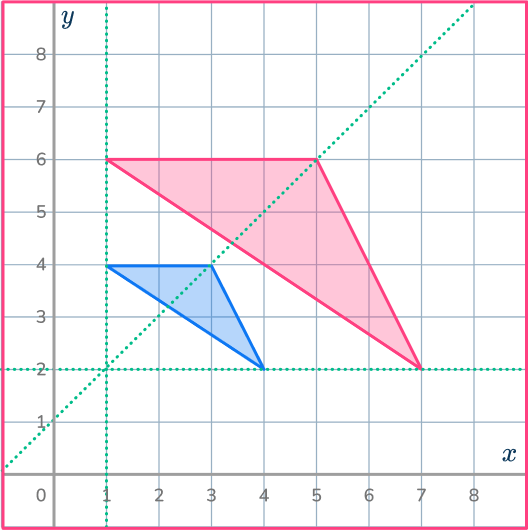
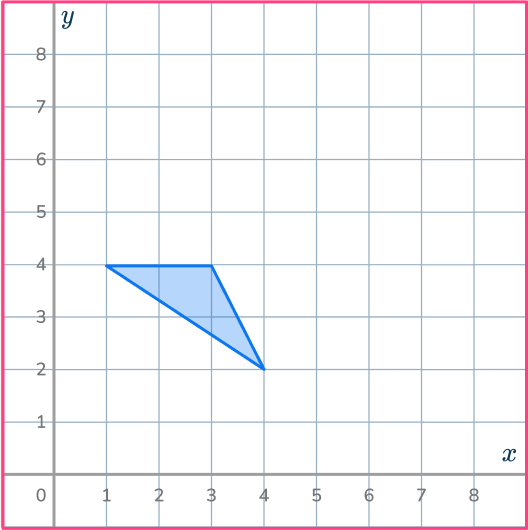
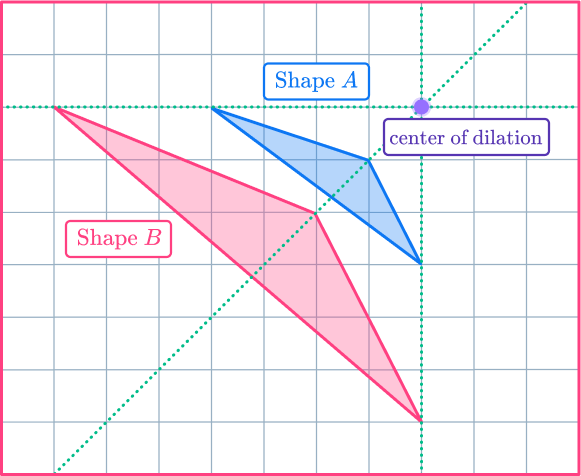
Example 5: find a center of dilation
Shape A has been enlarged to make shape B. Find the center of dilation.
Understand the problem.
Here, you have both the original shape and the dilation image and you must find the center of dilation.
Apply the dilation transformation or solve for the desired information.
Find pairs of corresponding vertices and draw ray lines going through the points.
Then, plot the center of dilation accordingly.
Example 6: negative scale factor (ADVANCED)
Enlarge the shaded shape with scale factor – 2 about the center of dilation.
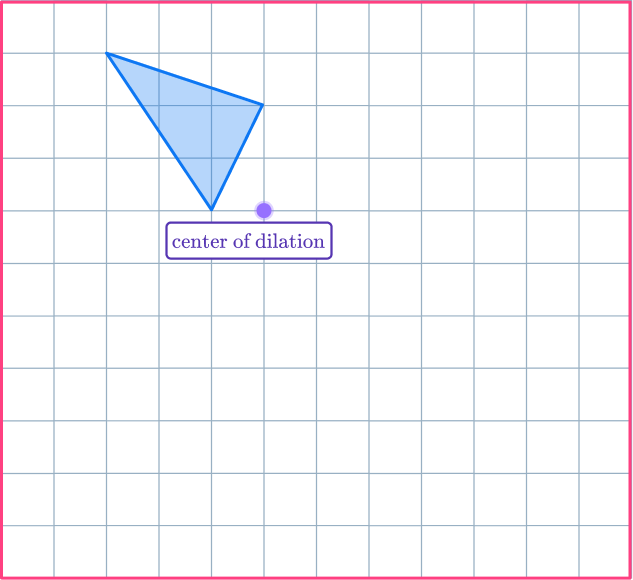
Understand the problem.
This is an advanced problem, as there are also negative scale factors in higher grade levels. These are an extension of positive scale factors.
When performing a dilation with a negative scale factor, you will resize the figure and also flip it across the center of dilation.
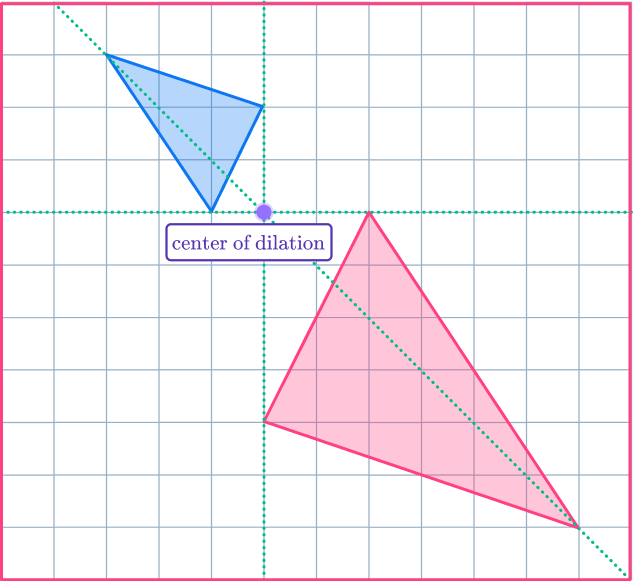
Apply the dilation transformation or solve for the desired information.
Draw ray lines from the center of dilation through the vertices of the original shape.
Extend the ray lines backwards through the center of dilation, as this is where the new points will go.
Teaching tips for dilations
- Start with basic polygons like triangles and rectangles. This makes it easier for students to see the effects of dilation before moving on to more complex figures.
- Use interactive tools or video lessons to visually demonstrate how changing the scale factor and center of dilation affects the figure.
- Educators can pose questions like, “What happens if the center of dilation is at a vertex?” or “How does the figure move if the center is outside?”
- After completing problems, ask students to explain the dilation changes. This reinforces their understanding and ability to articulate the concept.
Easy mistakes to make
- Inaccurate drawings
Use a sharp pencil and make use of the grid lines to help you to be accurate.
- Using diagonal lines
Diagonal lines can be tricky to enlarge, so it is best to use horizontal and vertical lines.
- Misunderstanding the origin
The origin of a coordinate grid has the coordinates (0,0), where the x -value and y -value are both zero. It is commonly denoted as O. It is used often as the center of dilation.
- Describing \bf{2} or more transformations
If you are asked to give a single transformation – make sure it is a single transformation, not 2 or more. Also, make sure that you state the type of transformation and give full details.
For example,
For enlargements state scale factor and the coordinates of the center of dilation.
Related transformations lessons
Practice dilations questions
1. Reduce the shaded shape by scale factor \cfrac{1}{2}\text{:}



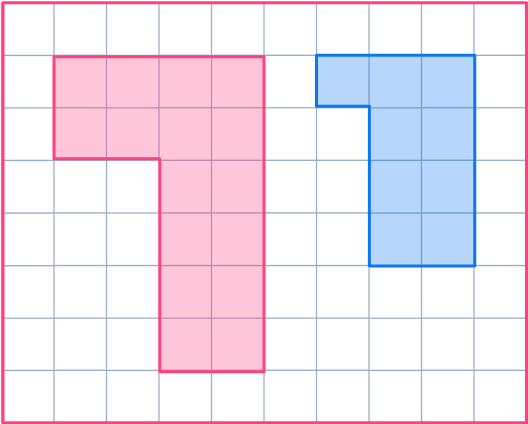

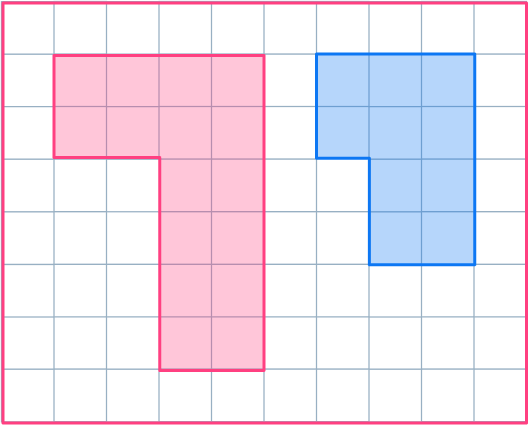

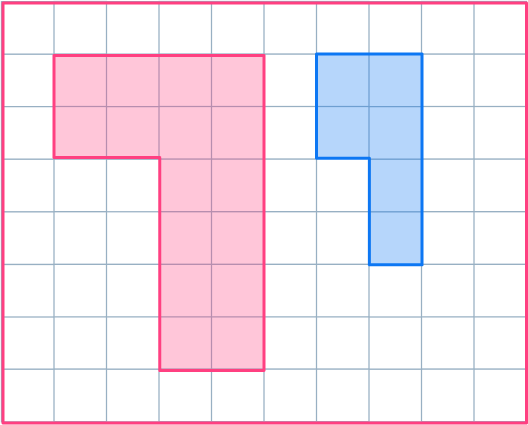

The scale factor is \cfrac{1}{2} , so all the sides need to be halved.
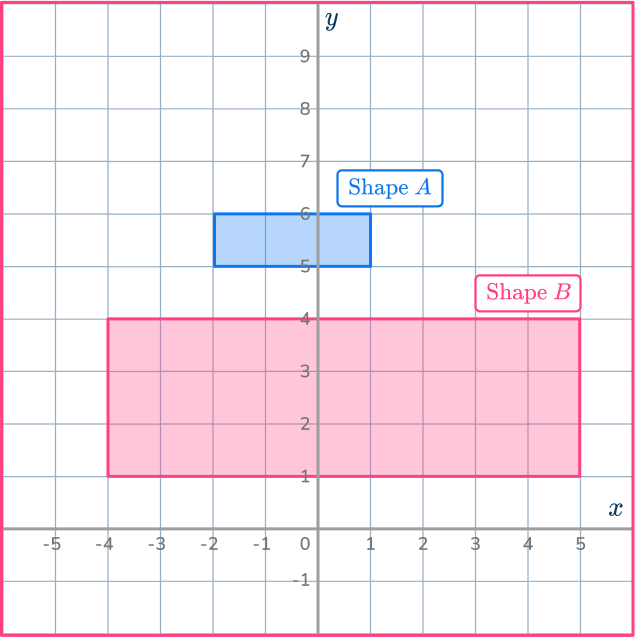
2. Shape A has been enlarged to make shape B. Calculate the scale factor.
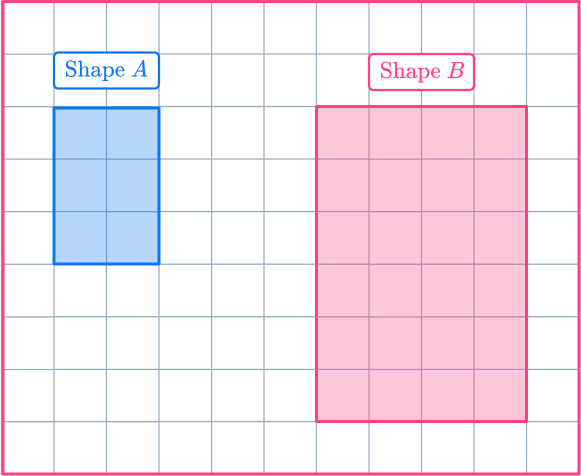
Scale factor is 3

Scale factor is 2.5

Scale factor is \cfrac{1}{2}

Scale factor is 2

To calculate the scale factor, you need to divide an enlarged length by the corresponding original length. If you use the heights of the rectangles:
scale \, factor = \cfrac{enlarged \, length}{ original \, length}=\cfrac{6}{3}=2
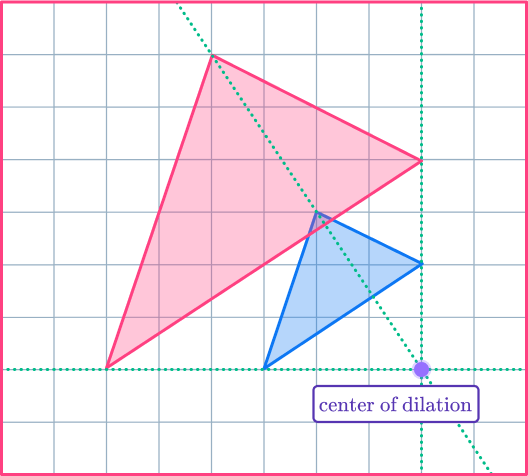
3. Enlarge the shaded shape with scale factor 2 about the center of dilation.
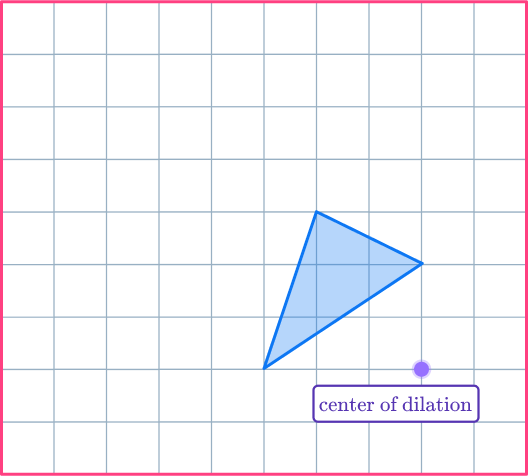
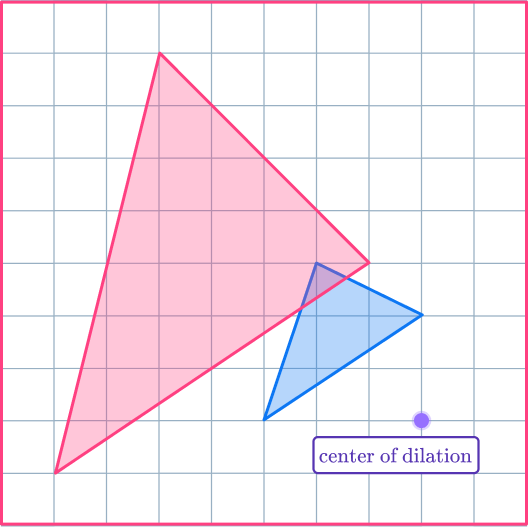




The two triangles should be similar. The pairs of corresponding sides are parallel lines. Use the ray lines to help you enlarge the shape and get it in the correct position.
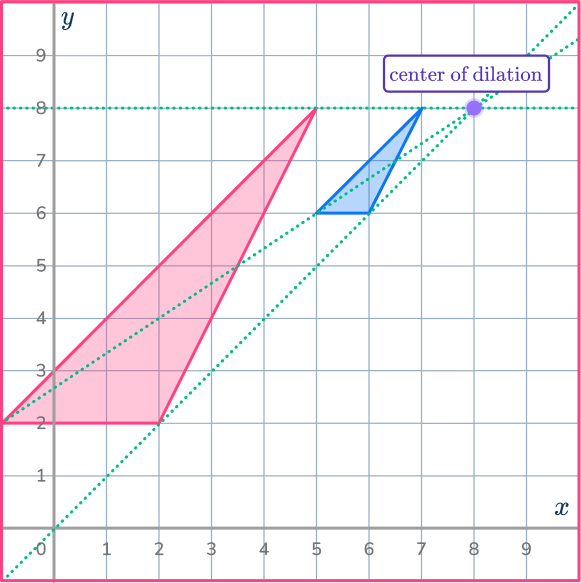
4. Enlarge the shaded shape by scale factor 2 about the point (8,8).
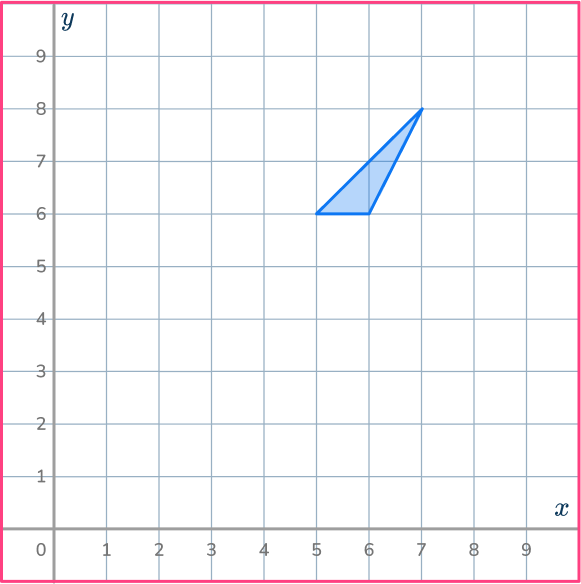
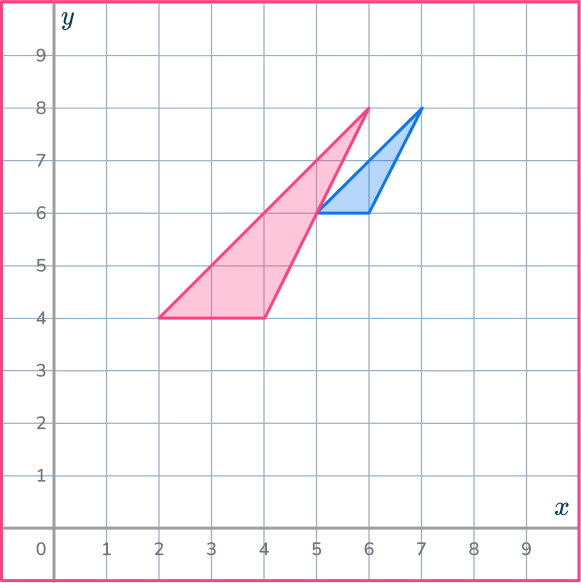

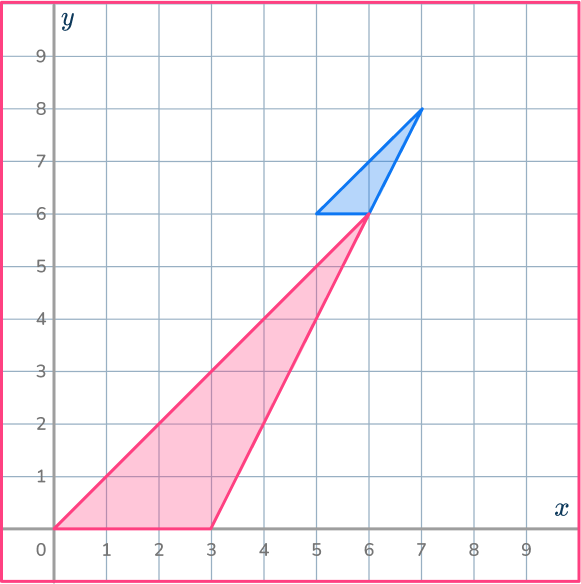

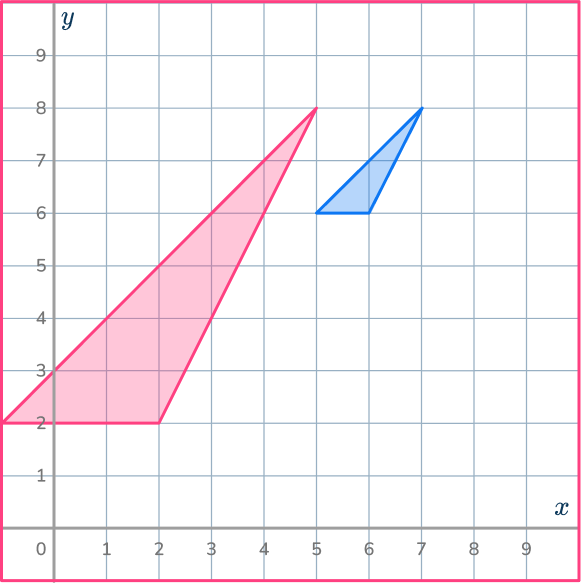

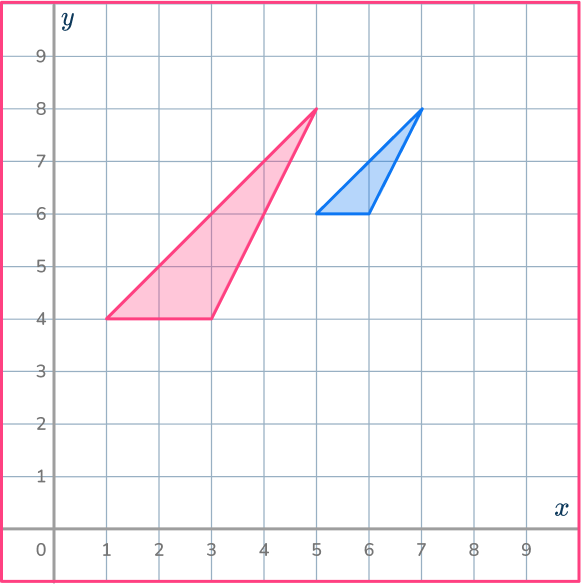

Make sure you have the center of dilation plotted correctly. Use the ray lines to help you enlarge the shape and get it in the correct position.
5. Shape A has been enlarged to make shape B. Find the center of dilation.




Find pairs of corresponding vertices and draw ray lines going through the points.
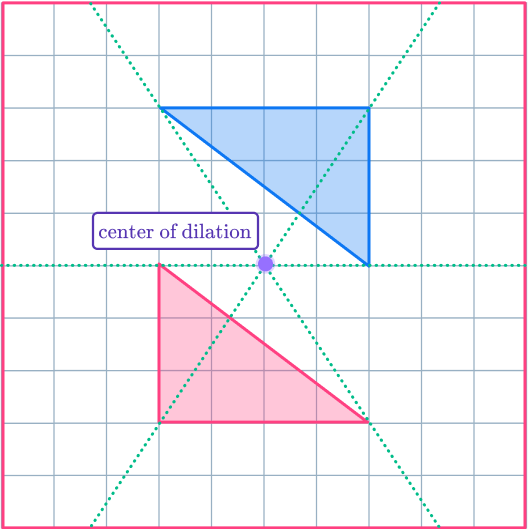
6. Enlarge the shaded shape with scale factor – \, 1 about the center of dilation. (ADVANCED)
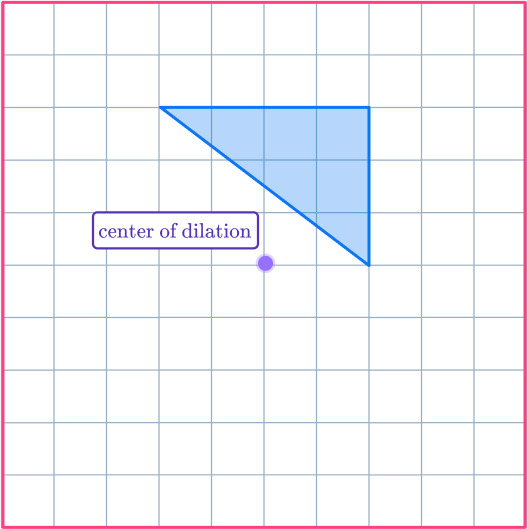
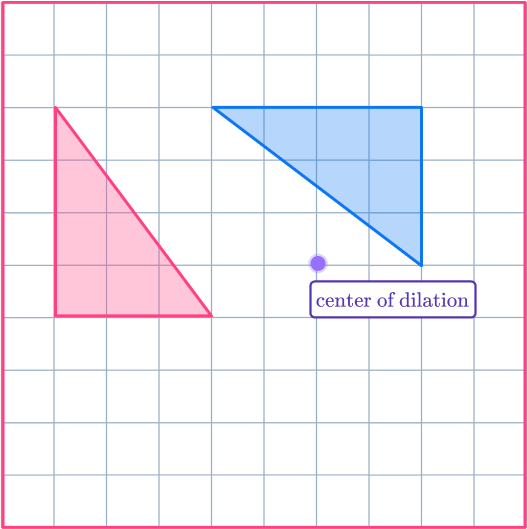

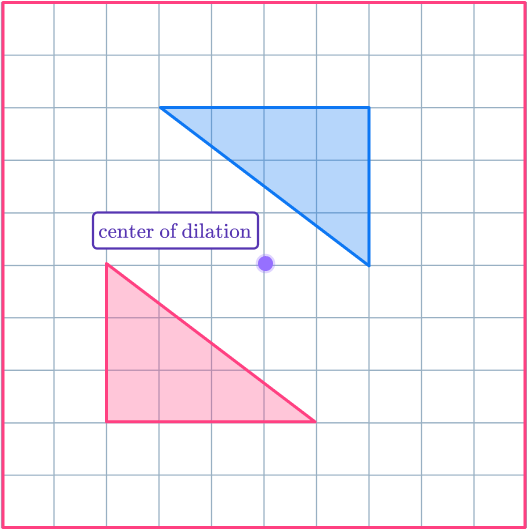

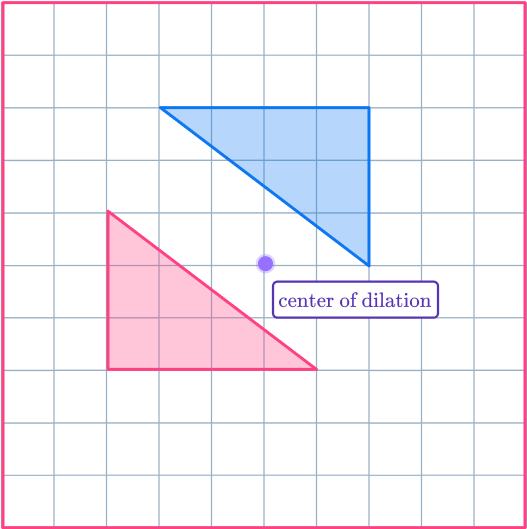

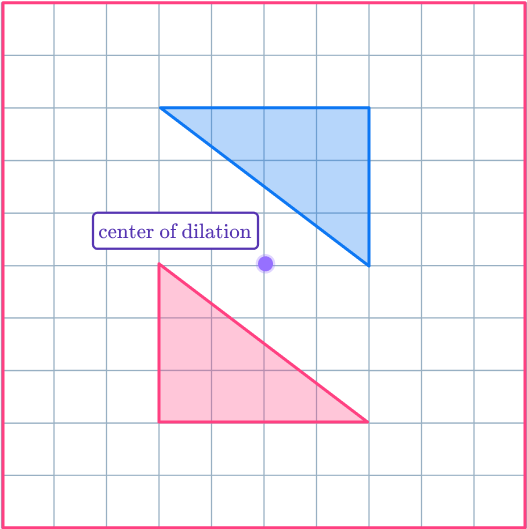

Draw ray lines from the center of dilation through the vertices of the original shape. Extend the ray lines backwards through the center of dilation, as this is where the new points will go.
Dilations FAQs
A dilation is a transformation that changes the original size of a shape by enlarging or reducing it while maintaining its shape and the proportionality of its sides. (Also called proportional stretching or shrinking.) The transformation is determined by a dilation scale factor and a center of dilation.
To perform a dilation, you need a center of dilation and a scale factor. Each point of the figure is moved along a line that passes through the center of dilation. The distance from the center to each point is multiplied by the scale factor to determine the new position of each point.
When the scale factor is greater than 1, the figure is enlarged. All points on the figure move farther away from the center of dilation, resulting in a figure that is similar to the original but larger in size.
When the scale factor is between 0 and 1, the figure is reduced in size. All points on the figure move closer to the center of dilation, resulting in a smaller but similar figure.
Yes, you can perform a dilation with a negative scale factor. It will resize the figure and also flip it across the center of dilation.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!