Algebraic proofs

Here you will learn about algebraic proofs, including proving expressions involving integers that are even, odd, or multiples of other numbers, and proving expressions with positive or square numbers.

Students will first learn about algebraic proofs as part of algebra in high school.

What are algebraic proofs?

Algebraic proofs are step-by-step logical arguments that use algebraic rules, properties, and theorems to demonstrate the truth of a mathematical statement or equation. Each step is justified with a reason, such as a property of equality or a previously established theorem.

You will be used to seeing equations in maths, written with an equals sign (=), such as in the equation x+2=5. An equation is only true for certain values of the variable – here, the statement x+2=5 is only true for x=3.

An identity is true for any value of the variable. For example, 2x+4x is always equal to 6x, no matter what values of x are chosen, so you could write this using the identity symbol (\equiv) as 2x+4x\equiv{6x}.

Note: You cannot balance an identity as if it were an equation because the equivalence sign \equiv has a different meaning than the equal sign =.

To prove an identity, you must only work on one side of the equivalence sign, and show that this is the same as the other side. This may also be to prove a statement such as “is an even number” or “is divisible by 5 ”.

You cannot carry out any operation on one side, such as multiplying by 2 or adding 3 to remove terms as this will make the identity invalid. You must only use algebraic facts to substitute, expand, factor, etc to show equivalence or prove a statement.

In order to prove that the sum of any two odd numbers is an even number, you cannot just pick a few numerical examples and show it works,

This is because you need to show that it works for every pair of odd numbers, instead of just the examples you’ve chosen.

To do this, you need to know how to express different types of integers algebraically.

You can let any integer be represented by a letter. You can use any letter you want.

For algebraic proof, we tend to use the letter n and may also use m if we need a second letter, but you can also use x, \, y, \, w, etc.

Even numbers

If you want to express an even number, you can call it 2n, because all even numbers are multiples of 2. A multiple of 3 would be 3n, a multiple of 4 would be 4n, etc.

Odd numbers

The odd numbers are always 1 above or below an even number. So you could call an odd number 2n-1 or 2n+1.

The diagram below shows how every integer from 1 to 10 can be mapped to an even number by multiplying it by 2, and subsequently to an odd number by subtracting 1.

This is true for every value of n, so we can state that every even number can be represented as 2n and every odd number can be represented as 2n-1.

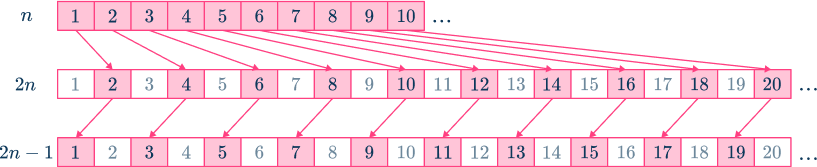
Consecutive integers

Consecutive means “one after the other”.

If you let n be any integer, the next integer will be n+1. The one before n will be n-1, etc.

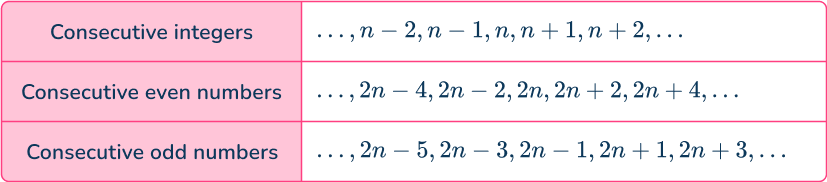
Let’s look at an example.

Prove that any two odd numbers add to an even number.

You need to have two different algebraic odd numbers. For this, you should use two different letters so that the odd numbers are not related.

Let’s use 2n+1 and 2m+1.

Adding these together gives 2n+1+2m+1=2n+2m+2.

To show that any expression is even, you just need to show that this expression is a multiple of 2. To do that, show you can remove a factor of 2 from each term.

So because you can factor out 2, it means the expression must be even.

Therefore, you have proved algebraically that the sum of two odd numbers is always even.

If each term in an expression has a factor of 3, every number that the expression represents is divisible by 3. For example, 3n+6 can be factored to 3(n+2) which is divisible by 3.

If each term in an expression has a factor of 4, every number that the expression represents is divisible by 4. For example, 16-20n can be factored to 4(4-5n) which is divisible by 4.

What are algebraic proofs?

Common Core State Standards

How does this relate to high school math?

• High School – Algebra – Reasoning with Equations & Inequalities (HS.A.REI.A.1)
  Explain each step in solving a simple equation as following from the equality of numbers asserted at the previous step, starting from the assumption that the original equation has a solution. Construct a viable argument to justify a solution method.

How to prove algebraically

In order to prove algebraically:

1. Think about what algebraic expression will prove the given statement.
2. Create an expression or manipulate a given expression.
3. Use a method of simplification, factoring, completing the square or otherwise to find an expression to prove the given statement.

Algebraic proofs examples

Example 1: prove an identity

Prove that (5n+2)^{2}-(4n+5)^{2}\equiv(3n-4)^{2}+4n-37.

1. Think about what algebraic expression will prove the given statement.

You need to expand the brackets on the left and collect terms. You then need to separate the terms to give the expression equivalent to (3n-4)^{2}+4n-37.

2Create an expression or manipulate a given expression.

Expand the left-hand side.

3Use a method of simplification, factoring, completing the square or otherwise to find an expression to prove the given statement.

Use the expanded expression for (3n-4)^{2}\equiv{9n}^{2}-24n+16 to find the remaining required terms.

Example 2: prove that an algebraic expression is a multiple of an integer

Prove that (2n+3)^{2}-(n-3)^{2} is a multiple of 3, where n is an integer.

Example 3: prove a worded statement algebraically

Prove that the difference of two consecutive square numbers is odd.

Example 4: prove a worded statement algebraically

Prove that the sum of four consecutive odd numbers is a multiple of 8.

Teaching tips for algebraic proofs

• Encourage students to identify which theorem they need to use before starting their proof. Ask them questions like, “Which theorem can help us solve this step?” or “What rule or theorem can we apply here?”.
  
  As students become more comfortable with theorems, challenge them to use multiple theorems in a single proof, helping them see how theorems build on one another.

• Use interactive proof activities or worksheets where students must physically move theorem cards to the appropriate steps in a proof. This makes the abstract concept of applying theorems more tangible and engaging.
  
  For example, have cards for the Substitution Property, Addition Property of Equality, and Multiplication Property of Equality, and let students match theorems to the steps of a given proof.

• Connect the idea of congruence in geometry to algebraic proofs to help students understand the concept of equivalence.
  
  For example, explain that just as two geometric figures can be congruent (having the same size and shape), two algebraic expressions can be algebraically congruent, meaning they are equivalent under certain operations or transformations.

• Emphasize how postulates are used in proofs: When students perform operations on both sides of an equation, they apply postulates, such as when they add or subtract the same number from both sides to maintain equality.

• Encourage students to test potential counterexamples when they are unsure about the validity of a mathematical claim.
  
  For instance, if someone claims that “the square of any number is always greater than the number itself,” students can use 0 or 1 as counterexamples to show this is not always true.

Easy mistakes to make

• Incorrect expression for odd and even integers
  A common mistake is to write n and n+1 for even and odd integers. It is important to remember that even numbers are multiples of 2 \, (2n) and odd numbers are an even number plus any odd number (2n+1).

• Errors when expanding squared brackets
  For example, when expanding (2n-1)^{2}, remember that this means (2n-1)(2n-1), and not just to square 2n and square - \, 1.

• Errors with signs when expanding squared brackets
  For example, when expanding (n-1)^{2}, remember that (- \, 1)^{2}=1 and not - \, 1.

Related mathematical proof lessons

• Geometry proofs

The next lessons are

• Area
• 3D shapes
• Area of a quadrilateral

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.