High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Writing linear equations
Here you will learn about writing linear equations, including what they are and how to solve them.
Students will first learn about writing linear equations as part of expressions and equations in 7 th grade.
What is writing linear equations?
Writing linear equations is when a mathematical situation can be described using algebraic expressions that can be simplified to the form px+q=r (slope-intercept equation) and p(x+q)=r. You can use the algebraic expressions and information about the situation to form an equation and then solve the equation to find the solution.
For example,
Here is a rectangle. It has sides 3x+1 and 2x-3.

Form a linear equation for the perimeter, P, in terms of x.
The perimeter is the sum of all the sides of the rectangle.
\begin{aligned}P&=2(3x+1)+2(2x-3) \\\\ &=6x+2+4x-6 \\\\ &=10x-4 \end{aligned}Find the value of x when P=36.
\begin{aligned}P&=10x-4 \\\\ 36&=10x-4 \end{aligned}Solve the equation to find the value of x, by using inverse operations.
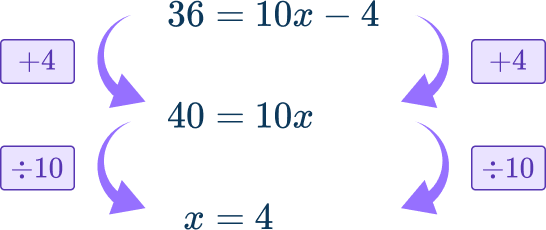
So, x=4.
Other equations can be written by applying facts from topics, such as:
- Angles
- Area
- Perimeter
- Volume
- Surface Area
- Compound Measures (such as speed, pressure or density)
- Sequences
- Probability
What is writing linear equations?

Common Core State Standards
How does this relate to 7 th grade math?
- Grade 7: Expressions and Equations (7.EE.B.4a)
Solve word problems leading to equations of the form px+q=r and p(x+q)=r, where p, \, q, and r are specific rational numbers. Solve equations of these forms fluently.
Compare an algebraic solution to an arithmetic solution, identifying the sequence of the operations used in each approach. For example, the perimeter of a rectangle is 54 \, cm. Its length is 6 \, cm. What is its width?
![[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)
![[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of solving math equations. 10+ questions with answers covering a range of 6th, 7th and 8th grade math equations topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)
![[FREE] Math Equations Check for Understanding Quiz (Grade 6 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Math-equations-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 8 students’ understanding of solving math equations. 10+ questions with answers covering a range of 6th, 7th and 8th grade math equations topics to identify areas of strength and support!
DOWNLOAD FREEHow to form and solve equations
In order to form and solve equations:
- Represent the situation algebraically.
- Use the information to write the linear equation.
- Solve the equation.
Writing linear equations examples
Example 1: ages
Abi is x years old. Rayan is twice as old as Abi. Cam is 3 years older than Rayan. The total of their ages is 58. Form an equation and solve to find x.
- Represent the situation algebraically.
The situation has three ages. You know that Abi is x years old and need to write expressions for the ages of Rayan and Cam.
Abi is x years old.
Rayan is twice as old as Abi. Therefore Rayan is 2x years old.
Cam is 3 years older than Rayan therefore Cam is (2x+3) years old.
You are given information about the total of their ages, so add the ages together.
\begin{aligned}&x+2x+(2x+3) \\\\ &=5x+3 \end{aligned}2Use the information to write the linear equation.
The total of the ages is 58. So, as 5x+3 and 58 both represent the total ages, they are equal to each other.
58=5x+33Solve the equation.
First subtract 3 from both sides of the equation.
Then divide both sides of the equation by 5.
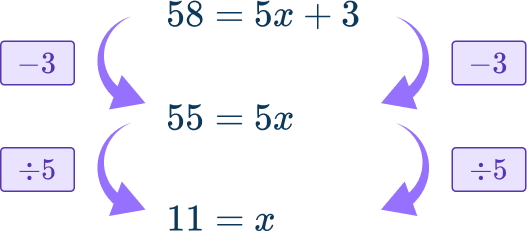
Check the answer by substituting it back into the original situation.
Abi is x years old and so Abi is 11 years old.
Rayan is twice as old as Abi and so Rayan is 22 years old.
Cam is 3 years older than Rayan and so Cam is 25 years old.
11+22+25=58Example 2: perimeter
This is a regular pentagon.
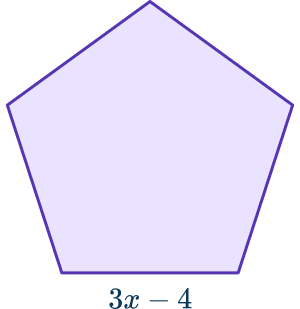
Each side is 3x-4.
The perimeter of the pentagon is 70.
Form an equation and solve to find x.
Represent the situation algebraically.
The situation is about the perimeter of a regular pentagon. Since it is regular, all the sides of the shape are the same. The perimeter, P, is,
P=5(3x-4)=15x-20
Use the information to write the linear equation.
The perimeter is 70 so, 15x-20 and 70 both represent the perimeter of the pentagon, they are equal to each other.
70=15x-20
Solve the equation.
First add 20 to both sides of the equation.
Then divide both sides of the equation by 15.
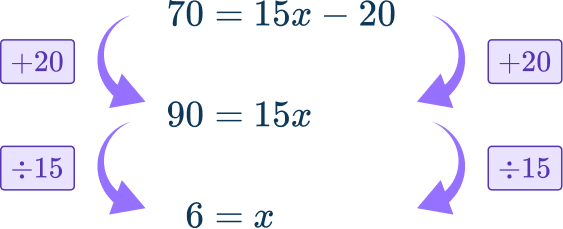
Example 3:
Kehlani has walked 102.5 miles this year. Each week, she walks 7.5 miles. It will take x weeks for Kehlani to walk 200 miles in total. Form an equation and solve to find x.
Represent the situation algebraically.
The 102.5 miles is a one-time distance that Kehlani has already walked. The 7.5 miles is a repeated distance that Kehlani walks each week. Since the number of weeks are represented by x, the additional miles walked each week can be represented by 7.5x. Using T to represent the total distance,
T=102.5+7.5 x
Use the information to write the linear equation.
The total miles Kehlani wants to walk is 200. So, you want to know when 102.5+7.5x is the same as 200, make them equal to each other.
200=102.5+7.5x
Solve the equation.
First subtract 102.5 from both sides of the equation.
Then divide both sides of the equation by 7.5.
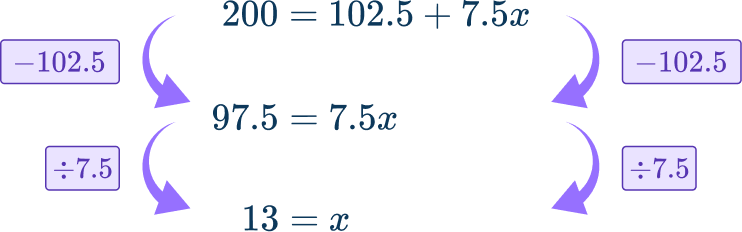
Example 4: parallel and perpendicular lines
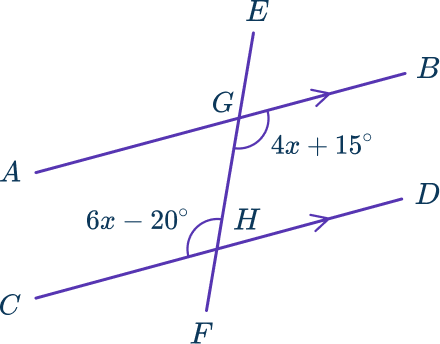
Lines AB and CD are parallel. The line EF intersects lines AB and CD at the points G and H respectively.
Form an equation and solve to find x.
Represent the situation algebraically.
The situation is about the parallel lines and angles. The two given angles, 6x-20 and 4x+15.
Use the information to write the linear equation.
As alternate angles are equal, the two angles given are equal to each other.
6x-20=4x+15.
Solve the equation.
First isolate x to one side of the equation, by subtracting 4x from both sides of the equation. Then add 20 to both sides. Finally divide both sides by 2.
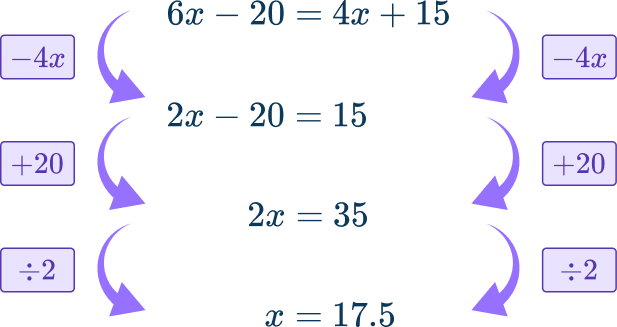
Example 5: probability
In a box there are only blue counters, green counters, red counters and yellow counters. Dana is going to take at random a counter from the box.
The probability of taking a red counter is twice the probability of taking a yellow counter.
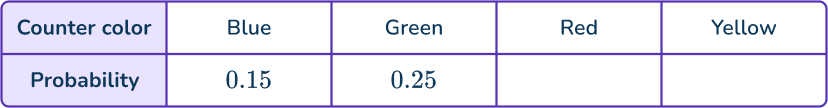
Form an equation and solve to find the probability that Dana picks a yellow counter.
Represent the situation algebraically.
The situation is about the probability of picking counters. You have not been given the probabilities for picking a red counter or a yellow counter, but you have some information.
Let the probability of picking a yellow counter be x. Then the probability of picking a red counter will be 2x.
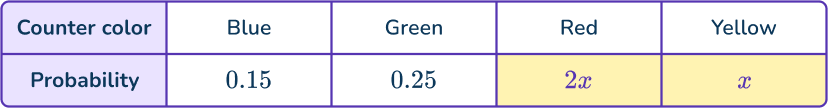
Use the information to write the linear equation.
These events are mutually exclusive, so use the fact that the sum of probabilities is 1 to write the equation.
0.15+0.25+2x+x=1
The left hand side of the equation can be simplified by combining the like terms.
0.4+3x=1
Solve the equation.
First subtract 0.4 from both sides of the equation.
Then divide both sides of the equation by 3.
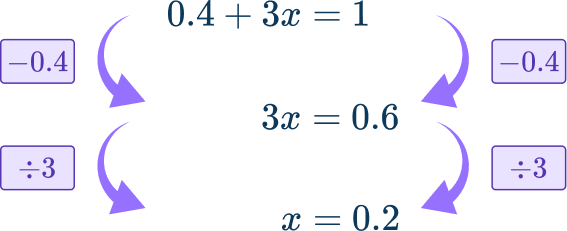
The question asks for the probability of picking a yellow counter, which is 2x.
Therefore, the probability of picking a yellow counter is 2\times 0.2=0.4.
The probability of picking a yellow counter is 0.4.
Example 6: averages
Charlie is 174\mathrm{~cm} tall. Harleen is x\mathrm{~cm} shorter than Charlie.
The mean of their heights is 169\mathrm{~cm}.
Form an equation and use it to find how tall Harleen is.
Represent the situation algebraically.
The situation is about the mean of two heights. Harleen’s height is 174-x\mathrm{~cm}. To find the mean, M, we find the total of the values and divide by the number of values.
M=\cfrac{174+(174-x)}{2}
The right hand side can be simplified to:
M=\cfrac{348-x}{2}
Use the information to write the linear equation.
As the mean is \cfrac{348-x}{2} and the mean is 169, they are equal to each other.
169=\cfrac{348-x}{2}
Solve the equation.
First multiply both sides of the equation by 2.
Then add x to both sides.
Finally, subtract 338 from both sides.
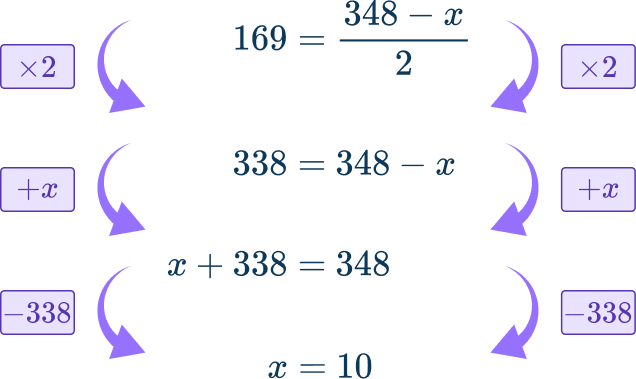
The question asks for Harleen’s height which is 174-x. Therefore, Harleen’s height is 174-10=164.
Harleen’s height is 164\mathrm{~cm}.
Teaching tips for writing linear equations
- While quality worksheets and practice problems have their place, be sure to connect linear equations to the real world. Find ways to make writing and solving them interactive and applicable to students’ lives.
- Even though students may not be graphing lines at this stage, you can still make helpful connections to the written linear equations. Let students know that the root of linear is “line” which is why the equations form straight lines on a coordinate grid. Also that the x and y values relate directly back to the location on the x -axis and y -axis.
Easy mistakes to make
- Forgetting that answers can be integers, fractions or decimals
Answers to equations can be integers, fractions or decimals. You can always check if your answer is correct by substituting the answer back into the original situation.
- Forgetting to simplify linear equations
Once you have written the situation using algebra, the algebraic equation should be simplified. This may mean expanding using the distributive property and/or simplifying by combining like terms or canceling out terms.
- Thinking an equation is not linear when the equation given is not in a certain format
Though commonly shown in slope-intercept, point-slope or standard form, a linear equation does not have to be initially shown this way. Any algebraic expression where the variables have 1 degree (or an exponent of 1 ).
- Confusing different terms for linear equations
Linear equations can also be referred to as linear functions or linear relationships.
Related math equations lessons
Practice writing linear equations questions
1. Use the information below to form and solve an equation to find Raj’s age.
Raj is x years old.
Sam is twice as old as Raj.
Tina is 2 years younger than Raj.
The total of their ages is 58 years.




The situation has three ages. You know that Raj is x years old and need to write expressions for the ages of Sam and Tina.
Sam is twice as old as Raj, so Sam is 2x years old.
Tina is 2 years younger than Raj, so Tina is x-2.
The total T of their ages is 58.
\begin{aligned}T&=x+2x+(x-2) \\\\ &=4x-2 \end{aligned}
As the total sum of their ages is 4x-2 and 58, they are equal to each other 4x-2=58
This linear equation can be solved,
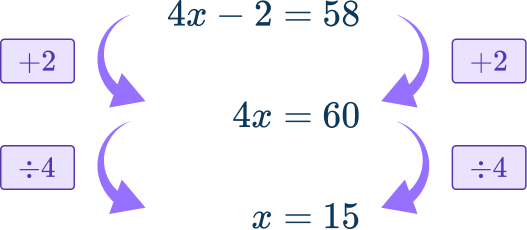
So the solution is x=15.
2. The perimeter of this regular hexagon is 108 \, cm. Form an equation and solve to find x.
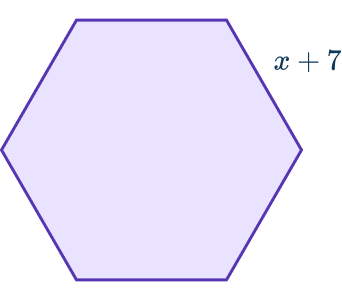




The shape is a regular hexagon. To find its perimeter, P, we can multiply the side length by 6.
\begin{aligned}P&=6(x+7) \\\\ &=6x+42 \end{aligned}
As the perimeter is 6x+42 and 108, they are equal to each other.
So the equation is 6x+42=108.
This equation can be solved,
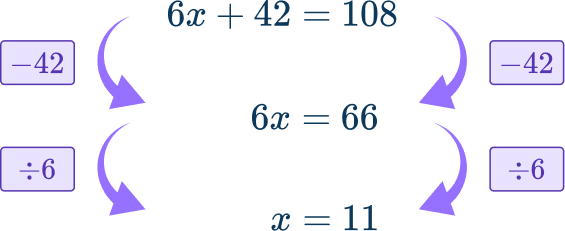
So the solution is x=11.
3. Hector made a \$ 1,750 down payment on a car. He pays \$ 345 per month. How many months, m, will it take him to pay for the entire car, which cost \$ 13,289?
Form an equation and solve to find m.




The \$ 1,750 is a one-time payment. The \$ 345 is a repeated payment that Hector makes each month. The number of months is m and the total of the monthly payments can be represented by 345m.
Use T to represent the Total amount paid. Then,
T=1,750+345m
Hector needs to pay \$ 13,289 in total. So, as the total amount is 1750+345m and \$ 13,289, they are equal to each other.
13,289=1,750+345m
This equation can be solved,
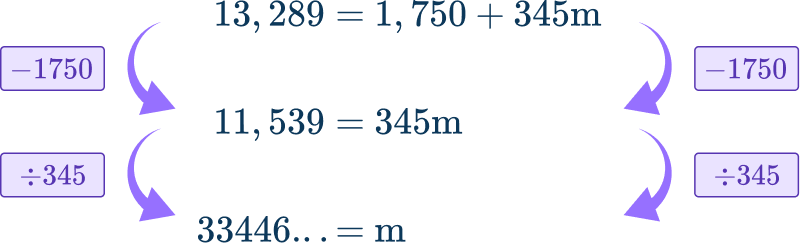
Hector needs to pay the entire amount, so it will take 34 months.
4. Lines AB and CD are parallel. The line EF intersects lines AB and CD at the points G and H respectively.
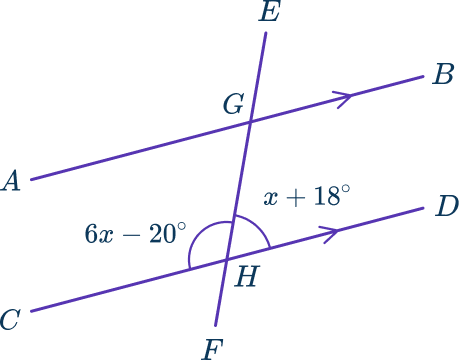
Form an equation and solve to find x.




The two angles given are supplementary and therefore equal to 180^{\circ}.
Write the expressions and set them equal to 180.
\begin{aligned}6x-20+x+18&=180 \\\\ 7x-2&=180 \end{aligned}
This equation can be solved,
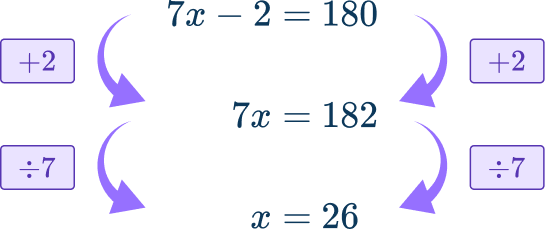
5. Here are the probabilities for picking different colored counters from a bag. The probability of picking a white counter at random is x. The probability of picking a black counter is three times the probability of picking a white counter.
Form an equation and solve to find the probability of picking a white counter.





This missing probabilities can be represented by x and 3x\text{:}

The probability of all the possible events adds up to 1.
Representing the total of probabilities as T,
\begin{aligned}T&=x+0.36+3x+0.12 \\\\ &=4x+0.48 \end{aligned}
As the total of probabilities is 4x+0.48 and 1, they are equal.
So the equation is 4x+0.48=1.
This equation can be solved,
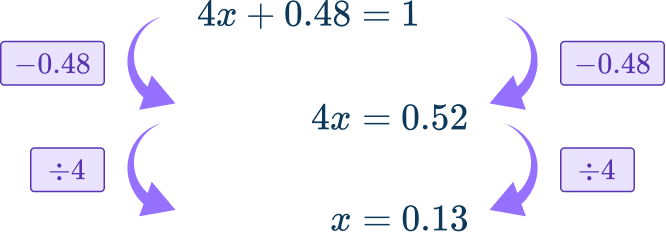
So the solution is x=0.13.
6. There are three bags of oranges.
In the first bag there are n oranges.
In the second bag there are n+5 oranges.
In the third bag there are 2n-3 oranges.
The mean number of oranges in the bags is 22.
Form an equation and solve to find n.




The total of the three bags is,
n+(n+5)+(2n-3)=4n+2.
\begin{aligned}\text{Mean}&=\cfrac{\text{Total}}{3} \\\\ \text{Mean}&=\cfrac{4n+2}{3} \\\\ 22&=\cfrac{4n+2}{3} \end{aligned}
So the equation is \cfrac{4n+2}{3}=22.
This equation can be solved,
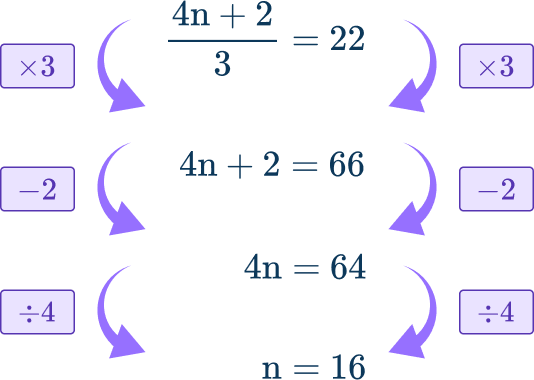
So the solution is n=16.
Writing linear equations FAQs
Students first learn about linear equations in 7 th grade and continue to work with them in 8 th grade, 9 th grade (Algebra 1 ) and beyond.
It is a form of linear equations. In this form, the slope m is the coefficient to x , and the y -intercept is the constant.
This is a different form for the equation of the line. This form is useful for a given point or ordered pair and the slope of the line. It is in the form y-y_{1}=m(x-x_{1}).
Slope of a line can be found with the formula \cfrac{\text{Rise}}{\text{Run}}.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!