Knowledge Organizers: What They Are And How To Use Them In Elementary School

Knowledge organizers are becoming more common in elementary school classrooms, having made their way from their roots in high schools. This article looks at what they are and how teachers can use knowledge organizers in elementary school teaching across the curriculum.

What are knowledge organizers?

Knowledge organizers are a summary of the key facts and essential knowledge that students need about a unit of work or a curriculum subject. They should be no more than one side of an A4 with all the information broken down into easily digestible chunks.

The single side of an A4 is important in order to focus the minds of the teachers creating them so they only include what’s absolutely crucial. It is easy for knowledge organizers to become overwhelmingly full of information which then makes them useless.

Knowledge organizers can be used for any subject knowledge or year group, from the humanities, such as history and english, to math and science.

It is also important to state what a knowledge organizer is not:

Knowledge organizers are not a curriculum and they will never replace the expert teacher. It’s best to think of them as tools to help teachers use a curriculum. 

Who uses knowledge organizers

Knowledge organizers can be a valuable tool for both children, staff and parents. Class teachers are usually the ones who write the knowledge organizer, to set out their expectations of what students should learn about a topic – and to clarify their own thinking around what is important.

School leaders, headteachers and subject leaders then may look at a series of knowledge organizers to check for progression and continuity both within and across curriculum subjects and to ensure standards and expectations for learning are being implemented, and if not, what continued professional development is required.

Students will review, revise and complete self-quizzing using their knowledge organizers.

And finally, knowledge organizers are a really clear and easy way for parents to be more aware of what their children are learning at school and thus to support them.

Knowledge organizer templates and examples

When downloading and using templates and free resources online, as with any other teaching resource, we encourage you to take a close look at these. It will always need adapting for your own school curriculum and the unit of work you are teaching.

What to include on a knowledge organizer?

The contents of a knowledge organizer are entirely subject and grade level dependent; while a lower elementary school knowledge organizer for phonics might simply include all the different phonemes to learn as its key knowledge, an upper elementary school knowledge organizer is likely to be a lot more complex, as fits the age of the learner and the information to be studied.

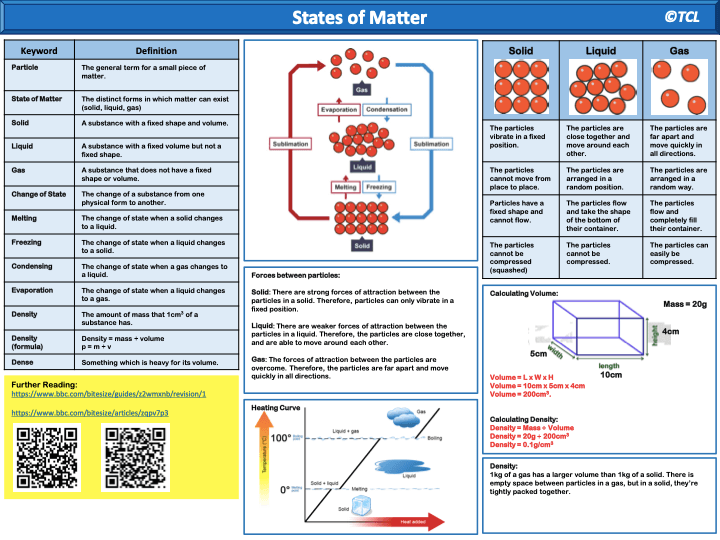
Knowledge organizer contents

There is of course some information that may be found across knowledge organizers in all subjects. This is a basic contents list.

• key vocabulary (in math make sure to use appropriate mathematical language by using this math vocabulary list)
• key places and people
• useful diagrams (as required for the topic)
• key dates for a subject like history (e.g. when the two World Wars were) would clearly also be included
• key themes – essential for any upper elementary school reading work
• important quotes (that demonstrate those themes)
• stem sentences for a subject like Math

Knowledge organizers used to be most common for humanities subjects, at the high school level. While there has been a recent increase in the use of knowledge organizers in teaching elementary math, there is still some misunderstanding about what to include and how to use knowledge organizers effectively at elementary school. 

Why use knowledge organizers?

There are a number of benefits to having students use knowledge organizers, many of these born from ideas developed from the teachings of cognitive science. Others draw from other sources but are still considered good practice, and we will look at these first.

5 benefits of using knowledge organizers

1. A knowledge organizer makes the teacher think hard about what will be taught

From a planning perspective, if it goes in the knowledge organizer, then there is an expectation that the students will learn it. With the limited space an A4 sheet of paper provides, the teacher needs to consider very carefully the information they include on the knowledge organizer. 

If it is not going to be used within a sequence of lessons, then there is no reason for that information to be in the organizer. Going through this thought process makes exactly what learning you expect to occur far clearer, and with this clarity the likelihood that what we teach will stick with students increases.  

2. Knowledge organizers are an endless source of meaningful homework activities

Once a knowledge organizer has been given to the students, the teacher now has an endless means of providing homework for the students.

Assuming that careful thought and consideration has been given to the knowledge included on the knowledge organizer, this will mean that students could come to a lesson already having some understanding of the key vocabulary or key facts needed to be successful for that lesson. 

Further, Professor Graham Nuthall in his work, Hidden Lives of Learners, hypothesizes that those students who know more about a topic, also learn more about a topic. Therefore, there is a chance that students could learn more from a lesson when they have some exposure to this information beforehand. 

Students’ working memory can process the bigger picture rather than getting distracted with the meaning of certain words, etc. This is an absolute work-load savior – no more last minute rushes to the photocopier and printing off 30 sheets of practice questions, which some students may not be able to do independently!

The fact that knowledge organizers are physical, printed out items, also ensures there is no barrier to uptake or technology requirement that might otherwise prove a barrier to disadvantaged children accessing the material during their home learning.

3. Knowledge organizers are an excellent tool for inclusion

For our low achieving students (by low achieving, I am referring to the differences between what students in the class know) use of knowledge organizers offers an excellent way to help fill those gaps. 

For example, those students who require more practice on ‘shapes’ could be given a knowledge organizer that details some core knowledge on shape names and properties of that shape, including angles. A teacher could then hand this to a teaching assistant to work with them on or get them to self-assess. 

It should be noted again, that this does not replace an expert teacher, but allows a student to take responsibility for their own learning and work on their own gaps.

In addition, once these facts and key words have been learned, it will be far easier for the expert teacher to teach and demonstrate (via worked examples and math talk) how to use this information to solve more complex problems and deepen learning. 

Assuming the key facts have been learned, there will also be less of a burden on students’ working memory, making it more likely they will learn to apply those facts when solving problems. 

If our aim is to use the mastery math approach, then we know that each student will need a different amount of time to master the content. By providing high quality knowledge organizers, we can ensure that those students who need more time can use their own time productively.

This also allows the use of the teacher’s time more effectively as the key facts will already have been learned.

4. Knowledge organizers create opportunities for spaced retrieval practice

Spaced practice refers to a specific practice concerned with timing – ‘when’ it’s best to learn. Is it better to spend seven hours on a Sunday to practice a skill before a test or to space those seven hours out as one hour sessions across seven days?  

Many studies have looked into this and the evidence is clear: it would be far better to practice for seven one-hour sessions than to practice for seven hours the night before. 

From the experiments by Ebbinghaus, we know that the rate we forget newly learned information is quick. Assuming 100% recall, it would only take 20 minutes (on average) for knowledge retained to fall to 58%. After an hour, the retention rate has fallen to 44%. Is it any wonder that students forget things? 

Luckily, there is a way to interrupt this forgetting and that is by systematically recalling that information which we wish to learn. This is known as retrieval practice and is far more effective in the long-term than simply restudying something (more on this later). 

When we retrieve information, that memory trace becomes stronger and the rate that we forget something decreases. The more we space out our learning, the more time it would take for us to forget something. 

Knowledge organizers are excellent tools to ensure that some of this spaced practice takes place.

Ahead of a summative assessment at the end of a topic, you can inform students that some of the questions will refer to previous learning; students can then refer to the knowledge organizer to access and practice those topics.  

This is especially important when dealing with topics in math that you know do not get equal teacher time. With the nature of curriculums and the popularity of blocking units, it is entirely possible that after two weeks on measurement in one year, the students will not encounter it again until the following year, outside of end of year and state assessments.

By continuously testing those areas that do not get our equal attention, we can ensure that the retention of these units happens across the year, not just in the unit.

5. Used appropriately, knowledge organizers can increase retention of facts

This comes down to their core purpose. Our working memory can only take in so much information at one time and for our students to be successful in a range of subjects they need to have a large store of factual knowledge in their long-term memory. 

Our minds have adapted to take this information from our long-term memory into our working memory without sacrificing much space within our working memory, but children need to develop this skill.

A child who has been taught their multiplication facts is far more likely to grasp equivalent fractions, as all their working memory can focus on the fractions. On the other hand, a child who is not secure in their multiplication facts will have to juggle both the multiplication facts and their relation to equivalent fractions in their working memory. 

This can overload the working memory, stressing its cognitive load and lead to students not learning what they should.

With a knowledge organizer providing the key information and, providing the students use them correctly, these facts can then become part of a student’s long-term memory.

How to use knowledge organizers

There are no set ways to use knowledge organizers, but there are some principles that ensure they are likely to be successful in their use. 

I would first of all suggest that a copy goes home and that one copy goes into a student work book. Some schools also put them on the school website for each year to further cement the links between home and school.

I would not advocate a teacher passing out a knowledge organizer and just telling their students to use it, especially in elementary school.

Telling students that they will have 5 questions from a certain section of the knowledge organizer can be an effective way to channel learning.

Students can then learn smaller chunks of the knowledge organizer as homework – which we have already established is more likely to ensure that they retain knowledge. 

It is important that, once you have set some sections of the knowledge organizer to learn for homework, that you also plan commutative quizzes; students must be made aware that they cannot just learn these facts in isolation to each other, and that there is an expectation to memorize them all for the long-term. 

A piece of math homework in week 4, for example, could be a selection of questions from the 3 previous weeks, with more weight given to section 1 and 2 as these may not have been tested for 2 weeks.

4 top tips for using knowledge organizers

1. For the knowledge organizer to be successful, students will have to put it away

A consistent finding in cognitive science is that of the retrieval effect. This has demonstrated that, when talking about long-term learning, the act of studying something for a session and then writing down everything from memory about that topic is far more effective than just constantly re-reading something. 

The latter gives us an air of familiarity about the topic and deceives us into thinking we know the material better than we actually do. To make sure that we do know the material, the knowledge organizer has to go away and a blank sheet of paper has to come out! 

Alternatively, a family member or care-giver could test students by asking questions from the knowledge organizer. This is the best way to help students retain more of the information they’ve learned. 

2. Give the knowledge organizer out at the start of a topic

As mentioned earlier, students who have greater prior knowledge of a unit are likely to learn more from the teaching of that unit. This is because knowledge is generative (sticky) and new knowledge is good at hooking onto this pre-knowledge. 

Without this foundation, there is nothing for knowledge to ‘hook’ onto, and so the new knowledge risks falling out of our minds. As teachers, we know that many students’ prior knowledge of a topic can vary and the home environment is one culprit for this. 

To ensure that all our students have a chance of being successful in an upcoming unit, I recommend that knowledge organizers go out a week before beginning teaching (maybe longer if the new unit coincides with a longer break) and sections of the knowledge organizer are given for students to learn that relate to the first few lessons. 

This way, there is a likelihood that all students have at least a baseline of prior knowledge, in which the new knowledge can attach itself to. However, this won’t happen by osmosis; this leads to my next tip.

3. Teach students how to use their knowledge organizers effectively

When introducing knowledge organizers for the first time, it is important that we teach students how to use them properly. This includes telling them the ‘why’. I have with previous classes told them all about working memory and long-term memory and the link between prior knowledge and new knowledge.  

This certainly gets some buy-in from the students and allows them to see that I am not just being utilitarian in my teaching outlook. Another crucial part is telling them about retrieval practice and helping them understand that to be successful, they will need to recall this information without using an organizer. 

This is important as research into retrieval practice has shown that  participants who had several sessions of retrieval practice believed they would remember less than those who took part in the research and had several sessions of simply re-studying information.  

This means that students over-estimate just how much they think they will learn. This makes taking the time to ensure your students know how to use knowledge organizers properly.  

For students to understand just how powerful knowledge organizers can be, they need to be able to use them and then work beyond them – coming back to that blank piece of paper!

4. Test regularly (but in the right conditions)

You need to make sure that your students know that you mean business when you provide a knowledge organizer. That means that from the get-go, low-stakes quizzing begins – the next day if possible. 

There should not be many questions – 5 at the most; doing this everyday after the knowledge organizer has been handed out will mean that your students know that they are expected to learn it. To get the conditions right, the students need to not feel threatened by the test (which is why we use the friendlier-sounding ‘quiz’ rather than ‘test’). 

This further means checking and scoring should not be a ‘public’ activity; this risks making the quiz high-stakes again. 

What we are aiming for here is for students to strengthen their memory, not for us to be assessing constantly. Other ways to get the conditions right are to make the quizzes time effective; I’d suggest that the ideal time is around 5-7 minutes to complete and mark a quiz. 

It’s also important to ensure that everyone is able to take part in these quizzes. This could be done through writing the quiz on paper and giving it to the students, or having multiple choice questions with students holding up the correct fingers to show the correct answers/writing their answers on whiteboards.

Feedback must still be given to the students, as we do not want students recalling the wrong information. Two ways this could happen could be the teacher simply going through the answers, or the students self-checking answers by using the knowledge organizer that is in their work books. 

Of course, this latter way will only be effective if the learning culture in your classroom is right and the students are not tempted to cheat.

How to write a knowledge organizer

It is important to note that when the term ‘knowledge-rich’ is talked about, this does not simply mean facts.

There are two types of knowledge – declarative and procedural. Knowing the difference between these two will help make it clearer which knowledge should go into your knowledge organizer. 

Declarative knowledge is simply factual knowledge. In the domain of mathematics, this would be your number bonds, multiplication facts, knowing that all angles in a triangle add to 180 degrees, etc.

Procedural knowledge involves being able to know procedures. So “how do I do 3 digit by 2 digit long multiplication” or “how to find the missing angle of a triangle if 2 are already given to me”. 

When designing knowledge organizers, it is unlikely that students will garner much understanding from procedural knowledge being on there. That is just an attempt to replace a teacher with a piece of paper and it will not work. 

We therefore want to focus our knowledge organizer on declarative knowledge, as it’s this knowledge that will unlock the procedural knowledge and make that learning much richer in the classroom.

In terms of what these would look like on the page, there is definitely no set format and I think it would be wrong to try and force all teachers to use the same format as they should be. 

It is preferable that you adapt your knowledge organizer to the needs of the unit, rather than follow an arbitrary format.

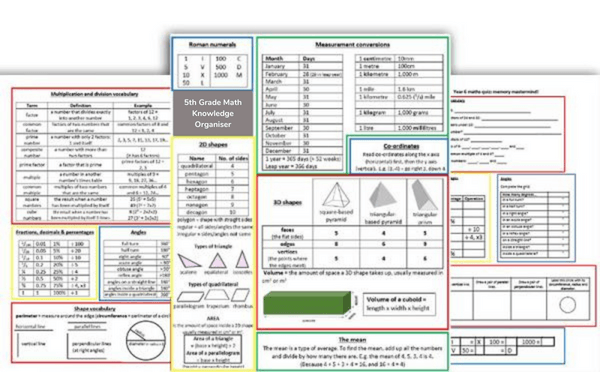
I would recommend, should you wish to create your own knowledge organizer, that you look at the curriculum objectives for each domain and grade and pick out which essential knowledge would be considered as declarative.

1st grade knowledge organizer math example: properties of shapes

These are the objectives for shapes for 1st grade for states following the Common Core Curriculum. Students should be taught to:

• Distinguish between defining attributes versus non-defining attributes
• Build and draw shapes to possess defining attributes.
• Compose two-dimensional shapes and  three-dimensional shapes to create  composite shapes, and compose new shapes from the composite shape.
• Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. 

If I were to create a knowledge organizer for this topic, I would ensure that I included the most common 2-D and 3-D shapes, a picture, a name, the number of sides, the number of edges, vertices and faces etc. 

The next objectives are examples of procedural knowledge. That is, the success of those final objectives comes down to students knowing the declarative knowledge from the first objective.

2nd grade knowledge organizer math example: number and place value

In 2nd grade, these are some of the learning objectives for number and place value for states following the common core standards. Students should be taught to:

• count from 0 in multiples of 5, 10 and 100; 
• Mentally add or subtract 10 or 100 more or less than a given number  
• recognise the place value of each digit in a three-digit number (hundreds, tens, ones) compare and order numbers up to 1000  
• read and write numbers up to 1000 in numerals and in words  

If I were creating a knowledge organizer as part of my number and place value teaching for 2nd grade, I would include all sums of two one-digit numbers.

I would also, where possible, follow my concrete representational abstract approach to include visual representations of these. I would include the greater than, less than and equal signs and a suitable definition along with a place value chart with a 3 digit number written in both numerals and words. 

Finally, I would provide spelling for the numbers 1-19 and the multiples of 10 up to 100. Again, I am under no illusion that this means that students will not need to be taught these things explicitly in lessons, it’s just that they are more likely to be successful if they have this background knowledge already in their long-term memories. 

While it can be a lot of work to begin with, the joy of having these knowledge organizers is that once they are done, they can always be reused year after year and will be a useful tool in the teacher tool box to help increase achievement in math or any other subject.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school lead teacher Neil Almond and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.