Building Thinking Classrooms: Effective Strategies For Your Math Classroom
Building thinking classrooms should be at the forefront of every school and district’s agenda. This student-centered, research-based approach to rich mathematics tasks dramatically shifts from traditional instruction. It requires teachers to rethink how they introduce concepts and requires students to be active learners in the math classroom.
Thinking classrooms can transform mathematics classrooms. They shift away from traditional instructional strategies that inhibit or do not encourage student thinking.
This guide explores the research and theory behind building thinking classrooms and insights into how teachers can shift their instruction to increase student engagement and achievement using this method.
What is a thinking classroom?
A thinking classroom engages learners in thinking and learning together. Students learn through activity, discussion and student collaboration, not direct instruction.
The building thinking classroom pedagogy, created by Dr. Peter Liljedahl, professor of education at Simon Fraser University, focuses on collaborative problem solving to construct and deepen math knowledge. It invites teachers to act as guides rather than experts as learners build thinking skills alongside math knowledge.
For example, in a Thinking classroom, learners start with a problem to solve. Rather than the teacher instructing how to solve a problem step-by-step, they give students the information they need to solve the problem when they are ready to use it.
In a middle school classroom, students stand in front of various surfaces–whiteboards, poster-sized sticky notes, and the window. In each group, one student holds a whiteboard marker and draws the answer to a problem. At times, groups stop and look around the room. They may walk to another group and ask a question. The teacher moves from group to group. “Tell me about your process,” he says. This is a snapshot into a thinking classroom.
The Ultimate Guide To Metacognition
A guide to the key information teachers need to know about metacognition, specifically in regards to math teaching and learning. Includes practical tips and ideas to use with students to encourage them to think about their own learning more explicitly.
Download Free Now!Theoretical foundations of thinking classrooms
Dr. Peter Liljedahl compiled more than 10 years of research and collaboration in more than 400 K-12 classrooms to create and refine his approach to building thinking classrooms. Through thinking classrooms, Liljedahl explains a new way to engage learners according to how teachers assign and organize math tasks, and learners work together.
The idea is that thinking classrooms replace practices like I do, We do, You do lesson structures, long teacher-led lessons, or over-scaffolding activities. These result in learners who look to the teacher for answers instead of relying on their resources, knowledge, and thinking for ideas.
In Peter Liljedahl’s work, he observed math classrooms and his own instruction to identify nine elements that determine whether or not a classroom is a thinking classroom.
Tasks: The type of tasks that are assigned and when and how they are used;
Communication: How tasks are communicated to learners,
Groups: How groups are formed;
Workspace: Learners physical workspace;
Room organization: How the classroom supports or does not support student thinking;
Questioning: How questions are asked and answered during independent work time;
Hints and extensions: How teachers use hints and extensions as student work;
Leveling: how and when a teacher levels their classroom after learners complete a task;
Thinking classroom vs non-thinking classroom
| Element | Thinking classroom | Non-thinking classroom |
| Tasks | Students start work with a problem to solve | Learners complete practice tasks after teacher-led examples |
| Communication | Communication is verbal with some information provided in written form | Learners copy from a textbook or from the board |
| Groups | Groups are formed randomly each day | Teachers form homogeneous groups and learners work in their own groups each day |
| Workspace | Learners have access to lots of workspace to write on | Students work at their desks in notebooks |
| Room organization | The room is organized with no official “front” | Learners sit in rows facing the whiteboard where the teacher teaches |
| Questioning | Students seek help from other groups when they struggle | The teacher answers questions when learners struggle |
| Hints and Extensions | When students are stuck, the teacher prompts them to look around the room for a hint. If they finish early, they answer a question extending the problem they just worked on. | Teachers provide answers, not hints; the only extension is the next practice question in the book |
| Leveling | Learners are grouped to “level” themselves | The teacher demonstrates the correct way to solve a problem |
| Assessment | Assessment focuses on processes and explaining learning | Assessment focuses on product and whether the student can replicate the math skills taught |
Thinking classroom framework
In the framework for building thinking classrooms, Liljedahl points out the importance of collaboration and problem solving in learning. Problem solving is a highly social activity where context matters (Leljedahl & Cai, 2021).
When students form collaborative groups and use their own whiteboard space and resources outside of the group, they are collaborative both in their group and across groups to solve the problem (Pruner & Liljedahl, 2021).
Thinking classrooms are highly interactive, with many different workspaces and opportunities for engagement. Research supports a highly interactive classroom as students construct ideas and learn from each other (Valbekmo & Bjuland, 2023).
In addition, research supports providing students with opportunities to explain their thinking as they engage in math problem solving. Collaboration that requires students to listen to others’ ideas and justify their own thinking supports student learning (Webb et al., 2021).
Finally, the use of non-permanent vertical workspaces (e.g., whiteboards) to engage in learning is a strategy to make students’ thinking visible to others in the classroom is relatively new. However, research supports the use of vertical workspaces to support student work, persistence and collaboration compared to when working at desks (Liljedahl, 2016).

Meet Skye, the voice-based AI tutor making math success possible for every student.
Built by teachers and math experts, Skye uses the same pedagogy, curriculum and lesson structure as our traditional tutoring.
But, with more flexibility and a low cost, schools can scale online math tutoring to support every student who needs it.
Find out moreKey components of thinking classrooms
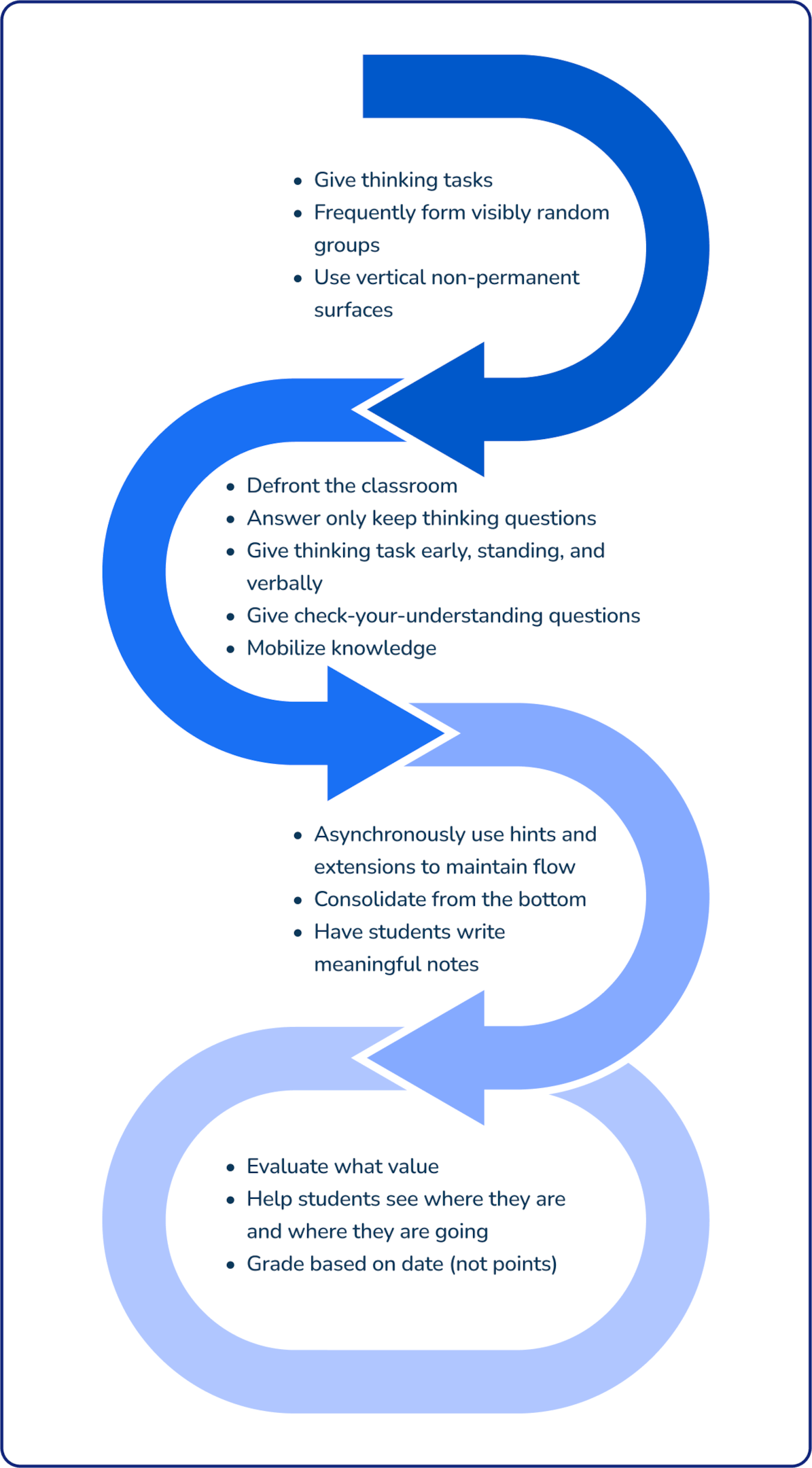
1. Start with thinking tasks
Instead of starting lessons with direct instruction or rote memorization, actively engage learners and begin lessons with problem solving.
At the start of the school year, have them solve non-curricular tasks. Starting with non-curricular tasks teaches students how to work together, communicate, and what to do when they get stuck, without students worrying about their math skills or getting things “right.” This creates a low-stakes learning environment learners will need to be encouraged to take risks on academic tasks later in the year.
Once students know how to work together, have them work on academic tasks. Provide the problem and any information that students may need to solve it. The first problem they work on should be simple, and become incrementally more challenging as they progress.
The problems worked on must be “problems worth solving,” meaning they are accessible, and allow students to apply multiple math strategies, and ultimately experience success. Problems worth solving area also motivating, either because of how they are engaging with math or because of how they relate to the problem.
3rd grade example
In a third grade class, learners are working on arrays. The math teacher posts this problem: A milk crate can hold 36 bottles of milk. Can you arrange 14 bottles in the crate so that each row and column has an even number of bottles?
Students break into groups with manipulatives and an example of an array to work with. This problem is a “problem worth solving” because it targets math and critical thinking skills needed to master it. It is a problem students can talk about as there are multiple approaches they can use to solve it.
Once students have completed that problem, they can tackle a more complicated task related to arrays.
8th grade example
In an 8th grade classroom, there is a significant number of students who play basketball and are familiar with the game. The teacher gives them this problem:
Bill, Sam and Rob all play for the school basketball team and are consistent free throw shooters.
- Bill always misses one shot and then makes one shot.
- Sam always misses two shots and then makes one shot.
- Rob always misses three shots and then makes one shot.
They practice their free throws in rounds where each gets one shot per round. Predictably, all three boys miss in the first round and each stays on their usual pattern for the rest of the rounds. After 16 rounds they stop to compare the baskets they have made in each round.
- What if they played more than 6 rounds?
- What about 57 rounds?
This problem is engaging because of the topic. It is worth solving because of the skills needed to solve it.
2. Collaborative groups
Collaboration is key to a thinking classroom. When learners work collaboratively, they build knowledge by combining what they know at the start of the task with what they learn from each other. Student engagement also increases as they rely on each other and other groups to clarify information.
In thinking classrooms, groups are chosen randomly. Assigning random groups breaks down social barriers and increases knowledge mobility.
Ways to select random groups:
Choosing popsicle sticks with student names on them;
Use a deck of cards, each student with an ace forms one group;
Use an interactive number generator.
3. Student engagement
In a traditional math classroom, desks are likely arranged in rows while a teacher explains how to solve a specific problem. The teacher may model problem solving, before assigning a task off to a student who completes the task with support from the teacher and then on their own.
However, in a thinking classroom, learners talk together to solve a problem and a teacher works with students to stimulate their thinking.
A teacher may assign a gallery walk to one group to stimulate thinking if they get stuck, or the teacher may have all students come to the center of the room and explain what they are working on. These approaches put the responsibility for student learning with students, rather than the teacher.
| Thinking task | I do, we do, you do task |
| The teacher presents a problem. Students write the problem on their vertical workspace and start to suggest ideas for how to start. As they work, the teacher circulates to observe. When one group gets stuck, the teacher suggests they talk with another group. When all groups have solved the problem, they share their process and results with each other. | The teacher presents a problem. The teacher models how to do the problem. Then, students are given a similar problem and walked through it with the teacher, copying her notes from the board. Finally, students solve a similar problem on their one. The teacher circulates and checks each students’ work. |
4. Non-permanent surfaces
A classroom environment must promote interaction. For example, using vertical non-permanent surfaces like whiteboards, flip chart paper or poster-sized sticky notes encourages collaboration as students gather around one workspace.
Each group of students uses the same workspace, so they are collaborating on the same problem rather than producing their own work. When students post their thinking and work, others can see it and either address errors or seek assistance from groups that are farther along in the problem solving process.
For example, tell a 3rd grade class to imagine they work at a cycling shop building unicycles, bicycles, and tricycles for customers. One day, you receive a shipment of 8 wheels. What are all the combinations of cycles you can make using all 8 wheels?
As they solve this problem, learners draw and write their work on their non-permanent surface. One student may draw bicycles to show the number of wheels, another student may use tally marks, and another may use numbers. When one group gets stuck, the teacher directs them to review others’ workspaces and ask questions of their peers. Having easy access to the entire class’s thought process encourages students to build critical thinking skills as well as math strategies.
The idea that they are not permanent encourages risk taking and reduces math anxiety or fear of giving an incorrect answer.
Examples of surfaces that can be used as non-permanent workspaces:
Whiteboards;
Windows;
Lockers;
Filing cabinets;
Shower curtains;
Shelf line;
Desktops.
5. Questioning strategies
In thinking classrooms, questions are open-ended, and meant to encourage independent thinking. The goal is to move away from the teacher asking all the questions to using effective questions as a thinking strategy.
Liljedahl identifies three types of questions:
Proximity questions: Students ask these when the teacher is close in proximity, like “is this right?” or “did we get it?”
Stop thinking questions: Closed questions that stop learners from thinking, like “will this be on the test?”
Keep thinking questions: Questions to regain momentum with the problem, like “how did you get that answer?” “what else could you have done to solve this problem?”
Thinking classrooms should use questions to enhance collaboration. Teachers do not respond to proximity or stop thinking questions. Instead, they use keep thinking questions to encourage deeper thinking and explanation. Using keep thinking questions also helps learners develop metacognition strategies, or the ability to explain their thinking, around what they are doing.
For example, a group of second graders are given this problem:
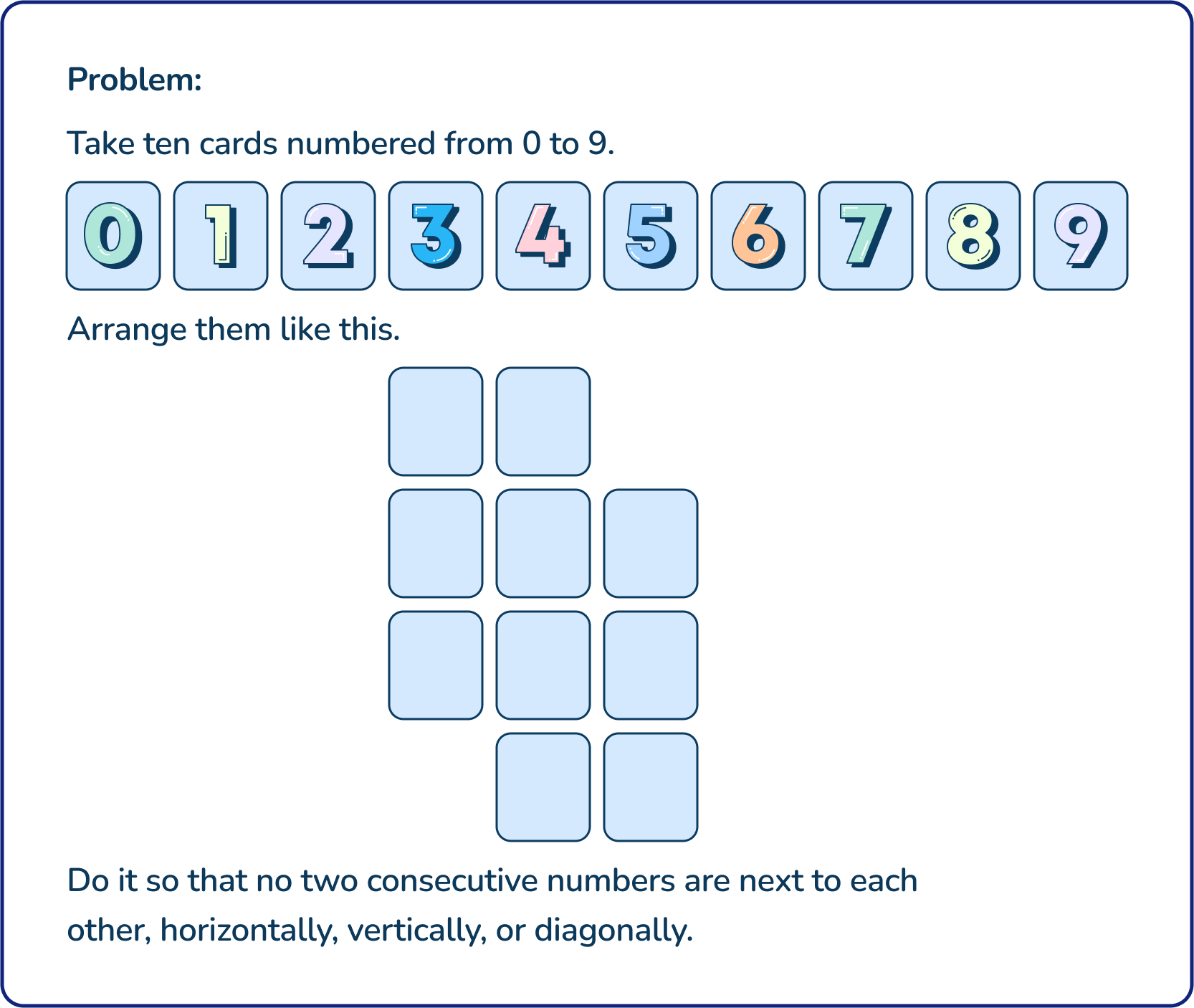
As the students work through the problem, the teacher circulates. When the teacher approaches one group, a student asks, “Is this right?” The teacher notices they are stuck halfway through the problem. The teacher prompts them with open-ended questions.
“What have you done so far? Tell me about your process.”
Then,
“what other way could you approach this problem?”
The students return to the problem, taking apart what they had done and starting over using a new approach.

Questioning with Third Space Learning
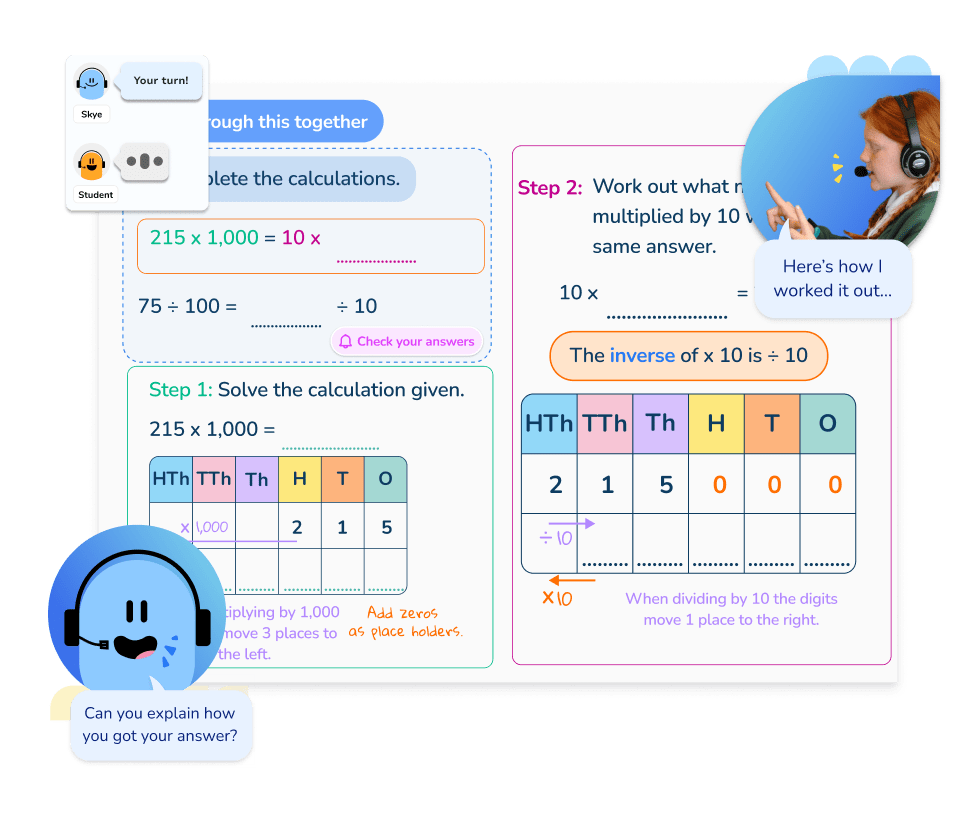
Skye, the AI math tutor, is trained to use effective, open-ended questions throughout Third Space Learning’s one-on-one math tutoring sessions.
Open-ended questions help promote a deeper understanding and encourage students to use critical thinking to explain how they reached an answer.
Schools receive a high quality headset for each student enrolled with Third Space Learning to ensure clear and effective communication through each session.
6. Evaluate student’s understanding
When every group has reached a minimum threshold, the teacher rearranges the groups to debrief. Teachers can assign each student a number, 1-4, and having all the ones, twos, threes, and fours get together to debrief.
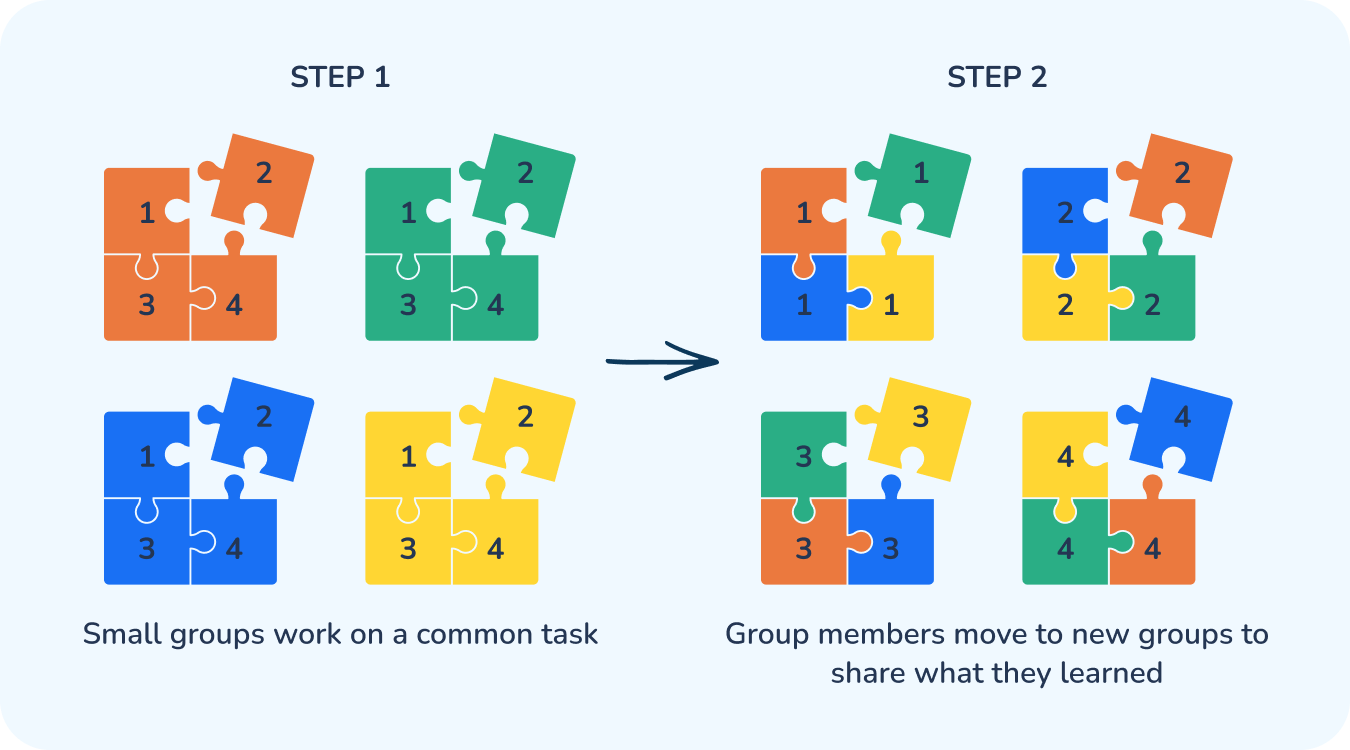
One strategy is to have each student take notes to their future self. This captures students learning but is much different than having them copy notes from the board.
When learners write notes to their future selves, they write them in a way that they can use in the future to solve similar problems. They may write information they learned or hints that were helpful.
Rather than each student having the same information written down, each student will have slightly different information on their page. But, they should be able to understand and use their notes effectively for later tasks.
Assessment in a thinking classroom
In a thinking classroom, assessment is meant to provide students with information about progress, not an evaluation of their answers. The focus is primarily on formative assessment.
Summative assessment focuses on process, not product and includes an evaluation of individual and group work.
Types of assessments in a thinking classroom include:
Observations of the process,
Checklists
Posters
Video or audio explanations
Photos or portfolios,
Written explanations of how a problem was solved,
A rubric that students complete for themselves and their peers.
The goal is for students to show their process, explain math concepts and their thinking, and reflect on their learning. Students can present as a group or provide individual reflections.
Building a mathematical thinking classroom
Third Space Learning’s approach uses the thinking classroom tenants to engage students in learning through problem solving and collaboration. Skye, the AI math tutor, serves as a guide and support as students apply math knowledge to solve relevant, interesting problems.
Mathematical task design and use
Start with the problem
Simply showing learners a problem and stepping back can start the shift to a more collaborative classroom.
Create classroom routines that students can apply to quickly move into problem solving mode and use the classroom space to facilitate group work.
Use hands-on tasks
In thinking classrooms, students are not provided with a lot of direct instruction, so provide tasks they can draw, visualize, or use manipulatives to solve.
For example, in this elementary task, students can use manipulatives to represent jelly beans and jars.
You have 16 jellybeans and four jars. Place the jellybeans in the jars so that each jar has either 3 or 6 jellybeans. Are there some things that are not possible?
Start with the skill
Choose a skill to focus on and build a problem around that skill. For example, if students are working on number sense, arrays, or geometry skills, they can work on this problem: How many squares on a chessboard? How many rectangles?

Use the real world for inspiration
The more relevant learning is, the better. Use learner-centered experiences as the foundation for problems. Scenarios from lemonade stands to sports to design are all learner-centered experiences that have real-world relevance.
For example, task high schoolers with the following problem: You want to arrange four candles on a cake. How many ways can you place the candles such that there are no more than two different distances between any two candles?
Classroom practices
Classroom arrangement, grouping, questioning, and consolidation are important strategies for a thinking classroom.
Here are some teaching strategies you can use to promote good classroom practices in a thinking classroom:
Create vertical, non-permanent surfaces: Turn lockers, walls and windows into work surfaces to invite collaboration and sharing.
Randomized groups: Create random groups so that learners work with different peers on tasks. This helps to increase knowledge mobility, break down social barriers and teache students to value each others’ contributions.
Strategic questioning: Ask open-ended questions that encourage explanations and reasoning such as: What do you notice? What questions do you have now? How can you solve this in a different way?
Real time feedback: Provide feedback to support learning in real time. This ensures students develop skills and practice them correctly.
Consolidate learning: Take time for students to share their work with the class, or to do a gallery walk to notice similarities between approaches. Stopping to consolidate knowledge ensures that students have a clear understanding of the topic.
Grade Level Considerations
Some teaching and learning strategies apply to all grade levels:
Collaboration;
Grade-level problems;
Vertical workspaces;
Consolidation.
And, some strategies will make thinking classrooms more successful with students of different ages:
Lower elementary school: As students learn how to collaborate, provide them with sentence starters and prompts to build language. Young learners also benefit from lots of modeling and pausing to notice what they are doing well so they can build collaboration skills.
Upper elementary school: Typically, older students have more language they can use to work together. Challenge them with open-ended questions that require them to explain their thinking.
Middle school: Support learners’ ability to work with and across teams by setting up as many vertical workspaces as possible. Encourage middle schoolers to give other groups feedback or ask each other questions.
High school: These learners can provide more depth and academic vocabulary to explanations. Challenge high schoolers to present their process and results in more than one way.
Challenges of a thinking classroom
Changing instruction to a thinking classroom can be a big change and comes with challenges. But, with perseverance and a growth mindset, thinking classroom can positively impact education throughout the grade levels.
1. Not giving it enough time
It takes time to implement new teaching and learning strategies. Make small changes first and one at a time. Start by putting up vertical workspaces, then think about the tasks you’ll provide. If you want to move to a fully thinking classroom within a school year, make gradual shifts in how you approach math instruction.
Reflect on how each change impacts how the class is engaging with math.
2. Relying on teacher talk
The shift to a student-centered math class can be difficult for teachers who are used to directing learning and instruction. It’s tempting to use closed questions and give plenty of instruction.
One way to make sure that you are using open-ended or keep-thinking questions is to use a clipboard with a list of keep-thinking questions as prompts. Put a tally mark each time you ask a Keep Thinking question so you can see how your questioning influences students’ work.
3. Supporting diverse learners
Students may need support with language or vocabulary as they learn how to explain their ideas and build confidence in their math skills. Providing visual supports for math vocabulary and sentence starters for students as they explain their ideas can help students who are building language alongside math skills.
Thinking classroom takeaways
A thinking classroom is a space where students are engaged in problem solving and critical thinking around math concepts, and where collaboration and contributions are valued.
Creating a thinking classroom, where learning is embedded into problem solving and where students take risks while solving challenging problems, takes time and practice. Teachers will need to model the same skills they want to see students demonstrate and support students through challenges.
But, the result, a classroom buzzing with math conversation and discovery is worth it.
Do you have students who need extra support in math?
Skye – our AI math tutor built by experienced teachers – provides students with personalized one-on-one, spoken instruction that helps them master concepts, close skill gaps, and gain confidence.
Since 2013, we’ve delivered over 2 million hours of math lessons to more than 170,000 students, guiding them toward higher math achievement.
Discover how our AI math tutoring can boost student success, or see how our math programs can support your school’s goals:
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Sources
Liljedahl, P. (2016). Building thinking classrooms: conditions for problem solving. In P. Felmer, J. Kilpatrick & E. Pekhonen (Eds.), Posing and solving mathematical problems: advances and new perspectives (pp.361–386). Springer. doi: 10.1007/978-3-319-28023-3_21
Liljedahl, P. (2021). Building thinking classrooms in mathematics, grades K–12: 14 teaching practices for enhancing learning. Corwin.
Liljedahl, P. & Cai, J. (2021). Empirical research on problem solving and problem posing: a look at the state of the art. ZDM, 53(4), 723–735. doi: 10.1007/s11858-021-01291-w
Pruner, M. & Liljedahl, P. (2021). Collaborative problem solving in a choice affluent environment. ZDM, 53, 753–770. doi: 10.1007/s11858-021-01232-7
Valbekmo, I. & Bjuland, R. (2023). Students’ Reasoned Dialogs During Problem Solving in a Norwegian Thinking Classroom. Nordic Studies in Mathematics Education, 28(1-2), 59–78. https://ncm.gu.se/wp-content/uploads/2023/07/28_12_059078_valbekmo.pdf
Webb, N. M., Franke, M. L., Johnson, N. C., Ing, M. & Zimmerman, J. (2021). Learning through explaining and engaging with others’ mathematical ideas. Mathematical Thinking and Learning, 1–27. doi: 10.1080/10986065.2021.1990744







