2nd Grade Math Curriculum Toolkit: Guidance, Tips And Resources For Elementary School Teachers

Teaching the 2nd grade math curriculum involves guiding 2nd graders through key moments of understanding, as they move from basic concepts to more challenging ideas, such as two-digit addition, and solving word problems.

2nd graders learn essential skills like addition and subtraction. They explore concepts like place value, telling time, and skip counting, and use mental strategies, number lines, and bar and picture graphs. These lay the foundation for future learning.

This blog provides practical strategies and resources for teaching math to this grade level. We cover how to correct common math misconceptions and share hands-on activities to incorporate into your lesson plans.

2nd grade math curriculum overview

In this blog, the 2nd grade math curriculum refers to the Common Core State Standards.

Here’s what every second grade educator is expected to teach:

Operations and Algebraic Thinking (2.OA)

• Represent and solve problems involving addition and subtraction.
• Add and subtract within 20.
• Work with equal groups of objects to gain foundations for multiplication.

Number and Operations in Base Ten (2.NBT)

• Understand place value.
• Use place value understanding and properties of operations to add and subtract.

Measurement and data (2.NF)

• Measure and estimate lengths in standard units.
• Relate addition and subtraction to length.
• Work with time and money.
• Represent and interpret data.

Geometry (2.G)

• Reason with shaped and their attributes.

Understanding the second grade math curriculum in greater depth

The Common Core 2nd grade math curriculum focuses on four main areas to build a strong foundation and prepare students for more complex concepts in later grades:

1. Addition and Subtraction: students use addition and subtraction within 100.
2. Place Value: understanding place value is crucial as students work with three-digit numbers and perform operations involving these values.
3. Measurement and Data: learners explore measurement concepts and begin to collect and interpret data through bar and picture graphs.
4. Geometry: students learn to identify and describe the attributes of basic shapes and explore partitioning and equal shares.

Challenges of second grade math 

Teaching second grade math comes with challenges, as educators navigate ways to address students’ common misconceptions.

Here’s a closer look at second grade math topics, including the most frequent misconceptions and strategies to help students overcome them.

As always, these insights are based on common core math standards but you can adapt to align with your state’s guidelines.

Operations and Algebraic Thinking (2.OA)

Represent and solve problems involving addition and subtraction

Using addition and subtraction within 100: Use addition and subtraction within 100 and apply basic problem-solving and reasoning skills to real-life scenarios to solve one-step and two-step 2nd grade word problems.

• Common mistakes: Using the wrong operation to solve the word problem.

For example, in the word problem: “Lulu has 22 stickers. She gives 5 to her friend. How many stickers does Lulu have now?” Students may use addition instead of subtraction.

• How to correct this: Use number lines to help students visualize the problem.

For example, on a number line, they can start at 22 and count back 5 spaces to see the number of stickers remaining:

Ask them to break down the problem step-by-step and have them practice with a variety of word problems.

Add and subtract within 20

Fluently adding and subtracting within 20: Use mental strategies to add and subtract within 20, and know from memory all sums of two one-digit numbers.

• Common mistakes: Struggling with recalling sums or mixing up numbers.

• How to correct this: Show students how to use mental strategies, such as making tens or using number bonds, to build fluency, and use quick quizzes to reinforce memory recall.

Determining whether a group of objects (up to 20) has an odd or even number of members: Understand odd and even numbers and write an equation for even numbers, showing them as the sum of two equal addends, like 8 = 4 + 4.

• Common mistakes: Not understanding how to pair objects to determine evenness, or not realizing that if every object can be paired with another, the number is even.

• How to correct this: Give students a set of objects like counters and have them pair them in groups of two.

If all objects pair up without leftovers, the number is even; if there’s one leftover, it’s odd.

Give them simple even numbers like 6 and ask them to find pairs of objects that add up to these numbers.

For example, have them pair six counters into two groups of three, then write the equations 6 = 3 + 3.

This hands-on practice helps them see that 2 equal addends make up even numbers.

Work with equal groups of objects to gain foundations for multiplication

Using addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns:

Add the number of objects in each row or column repeatedly to find the total when objects are organized into up to 5 rows and 5 columns.

Write this as an equation that expresses the total as the sum of identical numbers, equal addends.

• Common mistakes: Counting the rows or columns incorrectly.

• How to correct this: Use objects like counters to help students count and visualize the rows and columns. For example, give students 20 counters and a 5×5 grid mat.

Have them arrange the counters into equal rows, such as 4 counters in each of 3 rows, so they can see the array and then count the total:

Ask them to use addition to write the equation and find the total number of objects: 4 + 4 + 4 = 12

Number and operations in base 10 (2.OA)

Understand place value

Understanding the three digits of a three-digit number: Learn the concept of place value and understand that in a three-digit number, each digit has a different value depending on its position.

• Common mistakes in understanding the value of zero: Thinking that zero in a number like 330 is just a placeholder, not understanding that it represents the absence of ones.

• How to correct this: Use base-ten blocks or a place value chart to show that 330 has three hundreds, four tens, and zero ones. 

Emphasize that zero is important because it shows there are no ones, which helps maintain the correct place value of the other digits.

Counting within 1000; skip-count by 5s, 10s, and 100s: Skip-count by 5s, 10s and 100s, recognizing patterns in numbers.

• Common mistakes: Skipping numbers or counting in an irregular sequence.

• How to correct this: Use a number line or other visual aids to help students see the pattern.

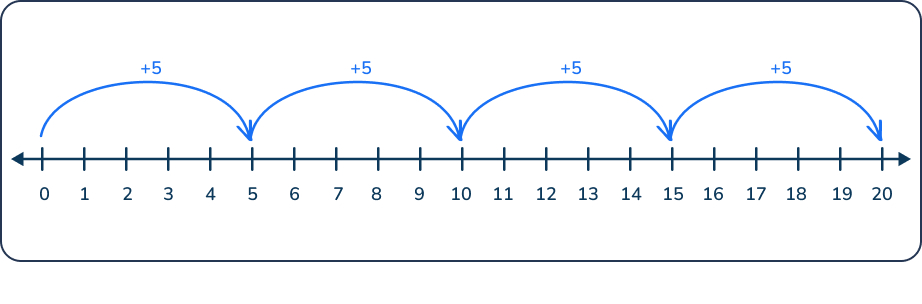
Use skip-counting songs or rhymes, and incorporate games where students must jump forward by 5s or 10s.

Read and write numbers up to 1000: Recognize, read and write numbers up to 1000 using:

• base-ten numerals
• number names
• expanded form

• Common mistakes in reading and writing numbers using base-ten numerals: Confusing the placement of digits, writing the wrong numeral as a result.

• How to correct this: Use base ten blocks or place value charts to demonstrate the correct placement or hundreds, tens, and ones.

Use activities where students need to use place value and represent numbers using base-ten numerals.

In Third Space Learning sessions, students work through a scaffolded example with their tutor and then try a similar question independently.

• Common mistakes in writing numbers in expanded form: Writing numbers like 345 in expanded form as 30 + 40 + 5, not understanding that the digit 3 in 345 represents 300, not 30.

• How to correct this: Use visual aids like base-ten blocks to demonstrate how 300 is made of three hundreds blocks.

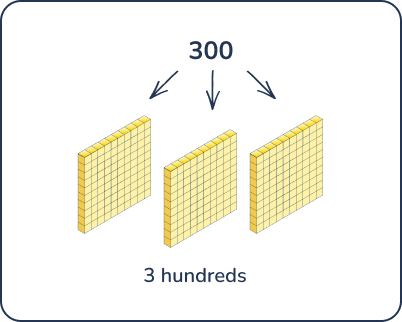
Build numbers with base-ten blocks and then write the expanded form together.

Comparing two three-digit numbers: Use the following symbols to show which number is larger, smaller, or if they are the same:

• >
• <
• =

• Common mistakes: Misplacing the comparison symbols due to confusion about which number is larger.

• How to correct this: Use base-ten blocks. For instance, have students build 374 and 482 using blocks. Then compare each place value and discuss which number is larger.

Using fun reminders can help, turn the greater than symbol into a crocodile and remind students that the hungry crocodile eats the larger number.

Use place value understanding and properties of operations to add and subtract

Fluently adding and subtracting within 100: Add and subtract numbers up to 100, using strategies based on:

• Place value, like understanding that 23 is 20 + 3
• Properties of operations, such as knowing that adding 10 is the same as adding one ten
• The relationship between addition and subtraction

• Common mistakes: Adding digits without considering their place value.

• How to correct this: Break down the numbers into tens and ones, demonstrating how to add each place value separately, and add the results.

For example, in 32 + 26, separate 32 and 26 into tens and ones (30 + 20 and 2 + 6).

Then, add the tens first (30 + 20) and then the ones (2+ 6).

Add the sums of the tens and ones to get the final answer (50 + 8 = 58).

Add up to four two-digit numbers:

Use digit addition strategies based on place value and properties of operations to add up to four two-digit numbers.

• Common mistakes: Adding numbers like 23 + 15 + 42 + 17 and forgetting to carry over when sums of tens exceed 10.

• How to correct this: Use manipulatives to show students when, why and how to carry over and how blocks are regrouped when they exceed 10.

Get students to practice adding two-digit numbers like 34 + 58 using place value strategies:

• Break down each number into tens and ones:

• Combine the tens and ones:

• Create one new group of ten from 10 ones:

• This leaves 9 tens and 2 ones, which is 92. So, 34 + 58 = 92

Teach them to write numbers in columns, aligning ones, tens, and hundreds, so they can clearly see where regrouping is necessary.

For example, show them 38 + 57 in column format:

Adding and subtracting within 1000: Add and subtract numbers up to 1000, using:

• concrete models or drawings
• place value
• property of operations
• the relationship between addition and subtraction

Understand that when adding or subtracting, you handle hundreds, tens, and ones individually, and occasionally require regrouping or carrying over.

• Common mistakes in subtracting within 1000: Forgetting to borrow when subtracting requires it.

• How to correct this:

Teach how to regroup using base-ten blocks or drawings.

For 48 – 16, show 48 blocks and explain that they need to take away 16 blocks.

Use worksheets with visual regrouping exercises. Demonstrate how to regroup from the hundreds place to subtract from the ones place.

Mentally adding and subtracting: Add or subtract 10 or 100 from numbers between 100 and 900 without needing to write it down.

• Common mistakes: Adding 100 to only the last two digits instead of adjusting all three digits. For example, when you ask a student to use mental math to add 100 to 245, they may add 100 to 45, without adjusting the hundreds place.

• How to correct this: Incorporate mental math drills into your lessons.

Provide quick, verbal exercises where students add or subtract 10 or 100 from a given number, like asking: “What is 100 more than 276?”, and tell them to use mental math strategies to focus on adjusting the hundreds digit, not just the last two digits.

Measurement and data (2.MD)

Measure and estimate lengths in standard units

Estimating lengths using units of inches, feet, centimeters, and meters: Use different units of measurement and compare these estimates to actual measurements to make reasonable guesses about the length of objects.

• Common mistakes: Overestimating and underestimating lengths, not understanding the scale of different units.

• How to correct this: Provide real life math activities where learners compare known objects to develop a sense of estimation.

For instance, show that a standard eraser is about 4 centimeters long and use this as a reference to estimate the length of other objects like a pencil:

Provide unit charts, and display rulers and measuring tapes, placing them next to common classroom objects so students can visualize different lengths.

Relate addition and subtraction to length

Using addition and subtraction within 100 to solve word problems: Solve word problems that involve measuring lengths in the same units.

• Common mistakes: Struggling to translate word problems into equations, not understanding what needs to be added or subtracted.
  
• How to correct this: Work with students on breaking down word problems into smaller steps. Show them how to use symbols like “?” or “x” to represent unknowns, and demonstrate how to mark equal intervals on a ruler and ask them to draw one.

Work with time and money

Telling and writing time: Read and write the time from analog and digital clocks, focusing on the nearest five minutes, and use a.m. and p.m. to indicate morning and afternoon times.

• Common mistakes: Misreading the positions of the hour and minute hands on an analog clock.
  
• How to correct this: Use analog clocks with movable hands for teaching time.

Solving word problems involving money: Solve money word problems using different types of coins and bills to find the total amount of money, and use $ and ¢ symbols correctly.

• Common mistakes: Miscalculating the total value of coins or using $ and ¢ symbols incorrectly, such as writing 35¢ as $35.

• How to correct this: Use real or play money when teaching money to sort and count different coins, and ask students to make a specific amount using various coins and bills. For example:

Represent and interpret data

Generating measurement data: Create a line plot, where the horizontal scale is marked off in whole-number units after gathering measurements.

• Common mistakes: Misunderstanding the line plot scale or recognizing that each tick mark represents a whole number and consequently placing data points incorrectly.

• How to correct this: Draw a large line plot on the whiteboard and have them place sticky notes with their measurements on the plot to visualize the data.

Using picture graphs and bar graphs (with single-unit scale): Collect data and display it using picture graphs and bar graphs to help visualize and compare information from up to four categories.

Solve simple problems by using the data presented in these graphs.

• Common mistakes: Not maintaining a consistent scale when creating bar graphs. For example, using different-sized blocks or uneven spacing.

Finding it difficult to create, read and interpret the graphs. This results in mistakes when solving “put-together,” “take-apart,” or comparison problems.

• How to correct this: Start with small, simple sets of real-world data and demonstrate how to create picture graphs and bar graphs. Show how they represent the same data in different ways.

Ask them to answer specific questions about the data, such as “How many more votes did grapes get than oranges?”.

Geometry (2.G)

Reason with shapes and their attributes.

Recognizing and drawing shapes: Identify and draw regular and irregular shapes with specific attributes, like a given number of equal faces or angles.

Recognize:

• triangles
• types of quadrilateral
• a pentagon shape
• a hexagon shape
• cube

• Common mistakes: Mixing up the names or properties of shapes, drawing shapes inaccurately, or miscounting the sides or angles.

• How to correct this: Use physical objects or cut-out shapes to allow students to count sides and angles, making it easier to differentiate between shapes.

Partitioning a rectangle: Divide a rectangle into equal-sized squares arranged in rows and columns, and count the total number of squares after partitioning.

• Common mistakes: Partitioning it unevenly, resulting in rows or columns that aren’t equal, and then, counting the squares incorrectly after partitioning.

• How to correct this: Provide learners with grid paper where they can divide rectangles into equal squares accurately.

Use math manipulatives like tiles or blocks to partition a rectangle, which helps them visualize equal rows and columns. After partitioning, ask them to count the squares by rows and then by columns.

During Third Space Learning online sessions, tutors first address prior learning to ensure students have a solid understanding of earlier concepts. This prepares learners to tackle more complex topics with greater confidence.

Partitioning circles and rectangles: Divide circles and rectangles into two, three or four equal shares.

Describe these parts using fraction terms, such as:

• halves
• thirds
• half of
• fourths

Understand that equal shares can look different depending on the shape.

• Common mistakes: Dividing shapes into unequal shares or fractions.
  

• How to correct this: Ask students to fold paper circles and rectangles to create equal shares. Show students various shapes divided into equal shares.

Third Space Learning lesson on partitioning circles and rectangles into equal shares

Teaching problem-solving in 2nd grade math

In 2nd grade math, developing problem-solving skills is essential as students begin applying mathematical concepts to real-world scenarios.

Here are 8 tips for teaching problem-solving and the 8 mathematical practices outlined in the CCSS effectively in second grade:

1. Make sense of problems and persevere in solving them

Encourage students to fully understand a problem before attempting to solve it.

• Use story problems: Create simple story problems relating to their everyday experiences, such as sharing toys. Ask them to discuss the problem and what they need to find out.

• Think-aloud strategy: Demonstrate solving a problem and verbalize your thought process.

2. Reason abstractly and quantitatively

Help students understand the relationship between numbers and use that understanding to solve problems.

• Number talks: Discuss different ways to solve addition word problems and subtraction word problems.

• Concrete examples: Provide manipulatives like base-ten blocks so learners can represent math problems physically before moving to abstract representations.

3. Construct viable arguments and critique the reasoning of others

Create an environment where students feel comfortable sharing their thought processes.

• Math partners: Pair students to think-pair-share together. Each partner explains their method, engages in math talk and then compares their answers.

• Classroom discussions: After solving a problem, hold a class discussion where students explain their reasoning and listen to others’ approaches.

4. Model with mathematics

Encourage students to represent real-world situations using mathematical models.

• Use objects for modeling: Provide learners with everyday items like coins to represent and solve simple problems.

• Drawing models: Ask students to draw pictures or diagrams to represent word problems. For example, ask them to draw groups of objects to illustrate subtraction.

5. Use appropriate tools strategically

Teach students to select and use various tools effectively to solve problems.

• Tool exploration: Introduce different tools, such as rulers and number lines. Let learners explore how each tool can help them solve specific problems.

• Choosing tools: Present a problem and ask students to choose the tool they think will best help them solve it. Discuss why they chose it and how it helped them.

6. Attend to precision

Emphasize the importance of being precise in calculations and explanations.

• Clear instructions: Teach learners to follow steps carefully and double-check their work.

• Precise language: Encourage learners to use precise mathematical language when explaining their thinking. For example, instead of saying “move the numbers,” they can say “regroup the tens.”

7. Make use of structure

Help students recognize patterns and structures in math to simplify problem-solving.

• Pattern recognition: Use activities that involve recognizing patterns, such as skip counting or finding patterns in shapes.

• Breaking down problems: Teach students to break down problems into smaller, more manageable parts.

8. Express regularity in repeated reasoning

Encourage students to notice patterns in their calculations and use them to solve problems more efficiently.

• Skip counting practice: Use skip counting to reinforce repeated addition.
  
• Reflecting on math strategies for problem solving: After solving a problem, ask learners to reflect on the strategy they used and consider if they could apply it to similar problems.

Hands-on activities for 2nd grade math

Second-grade math educators often use hands-on activities to allow students to explore and apply what they’ve learned. This helps them reinforce core concepts while enjoying math.

Here is a list of our favorite enrichment activities for 2nd grade:

Operations and algebraic thinking: solving word problems

Math storyboard

• Students create a storyboard for a simple word problem, illustrating each step of their problem-solving process.

This encourages students to break down problems and visualize each part of the solution.

Number and operations in base ten: addition and subtraction

Place value treasure hunt

Use this hands-on activity to strengthen place value understanding:

• Create a classroom treasure hunt; students follow clues that involve adding or subtracting within 100 using place value.
• Use examples like this: “Find the box with 27 blocks. Take away 13 blocks and see what you have left.”

Measurement and data

Classroom Poll

• Conduct a classroom poll on a favorite topic, such as favorite colors.
• Have students collect data and create a picture graph to represent the results.

Real-life activities integrate data collection and visual representation, making math investigations interactive and relevant to students’ interests.

Geometry: recognizing and partitioning shapes

Shape Sort and Build

• Give students a variety of geometric shapes.
• Ask them to sort them based on attributes like the number of sides or angles.
• Then, ask them to construct different structures, such as building a house using squares for walls and triangles for the roof.

Sorting and constructing shapes enhances students’ spatial reasoning and understanding of geometric properties.

Why we love teaching the 2nd grade math curriculum

Teaching second grade math provides an opportunity to build a strong foundation for young learners.

The challenge of addressing each student’s unique learning needs and common misconceptions is significant, but overcoming these hurdles and witnessing them succeed and grasp new concepts is highly rewarding

There is nothing like the satisfaction of knowing your efforts will have a lasting impact by helping students build a solid foundation in 2nd grade so they can tackle more complex topics later on.

How Third Space Learning helps students with the 2nd Grade math curriculum

Students progress at different rates, some may be working on skills from previous grade levels. One-on-one tutoring can offer targeted help where each student needs it most.

Third Space Learning’s one-on-one online STEM-specialist tutors help struggling 2nd grade students close gaps in their math understanding and accelerate progress.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?