One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Converting decimals to fractions Equivalent fractions Mixed numbers and improper fractions Square numbersThis topic is relevant for:

Rational Numbers
Here we will learn about rational numbers, including the definition of a rational number, examples of rational numbers, how to identify rational numbers and how to prove that a recurring decimal number is rational.
There are also rational numbers worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are rational numbers?
Rational numbers are numbers that can be expressed in the form \frac{a}{b} where a and b are integers (whole numbers) and b
Below are examples of a variety of rational numbers. Each number has been expressed as a fraction in the form \frac{a}{b} to show that it is rational.
| 3.2 = \frac{16}{5}
Terminating decimals | 7 = \frac{7}{1}
Integers |
|---|---|
| 0.\dot{3} = \frac{1}{3}
Recurring decimals | 4\frac{4}{5}=\frac{24}{5}
Fractions and mixed numbers |
If any of the above types of numbers are also negative numbers then they are still rational.
What are rational numbers?

Key points on rational numbers
Below are some key points on rational numbers.
- Not all fractions are rational numbers
All rational numbers can be expressed as a fraction, but not all fractions are rational numbers.

For example, \frac{5}{\sqrt{2}} is a fraction but it is not rational. The numerator is an integer but the denominator is not (the square root of 2 is irrational). Therefore this fraction does not meet the definition of a rational number.
- The denominator of a rational number cannot be zero
For rational numbers expressed as fractions in the form \frac{a}{b}, \ b must be a non zero integer because zero cannot be a divisor. (Try 5 \div 0 on your calculator and it will give you an error message).
The letter a however can be equal to 0 as we can divide 0 by any real number and get the solution 0. This means that 0 itself is a rational number.
- Numbers that are not rational are called irrational numbers
If a number cannot be represented as a fraction in the form \frac{a}{b} where a and b are integers, then the number is irrational.
There are a several famous irrational numbers including Pi ( \pi = 3.141...), The Golden Ratio (\varphi =1.618...), and Euler’s Number (e=2.718...) .
Surds are also types of irrational numbers. A surd is the root of a number which produces a non-terminating decimal.
For example,
\begin{aligned} & \sqrt{9} =3 = \text{rational} \\\\ & \sqrt{2} =1.414... = \text{surd} = \text{irrational} \\\\ & \sqrt{0.25} = \sqrt{\frac{25}{100}} = \frac{\sqrt{25}}{\sqrt{100}} = \frac{5}{10} = \frac{1}{2} = \text{rational} \\\\ & \sqrt[3]{64} = 4 = \text{rational} \\\\ & \sqrt[4]{30} =2.34034731932... = \text{surd} = \text{irrational} \end{aligned}How to identify rational numbers
In order to identify and then show that a number is rational:
- Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers - Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
Step-by-step guide: Writing a decimal as a fraction
Step-by-step guide: Changing a mixed number into an improper fraction
Explain how to identify rational numbers

Rational numbers worksheet

Get your free rational numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Rational numbers worksheet

Get your free rational numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERational numbers examples
Example 1: showing that a terminating decimal is rational
Show that 6.7 is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
- Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers
6.7 is a terminating decimal and is therefore rational.
2Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
6.7 = 6\frac{7}{10} = \frac{67}{10}Example 2: showing that a terminating decimal is rational
Show that 0.045 is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers
0.045 is a terminating decimal and is therefore rational.
Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
Example 3: showing that a mixed number is rational
Show that 3\frac{4}{5} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers
3\frac{4}{5} is a mixed number in the form C\frac{a}{b} where a,\ b and C are integers, and is therefore rational.
Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
Example 4: showing that a recurring decimal is rational
Show that 0.\dot{6} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers
0.\dot{6} is a recurring decimal and is therefore rational.
Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
Example 5: showing that a recurring decimal is rational
Show that 0.\dot{4} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify if the number is any of the following. If it is then it is a rational number.
● An integer
● A terminating decimal
● A recurring decimal
● A fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers
● A mixed number in the form \bf{C\frac{a}{b}} where \textbf{a,\ b} and \textbf{C} are integers
0.\dot{4} is a recurring decimal and is therefore rational.
Show that the number is rational by writing it as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers.
How to prove that a recurring decimal number is rational
In order to prove that a recurring decimal number is rational:
- Identify that the number is a recurring decimal. This is a non-terminating decimal that repeats the same digit or same set of digits after the decimal point.
- Write \bf{x =} the given number.
- Multiply \textbf{x} by a power of ten ( \bf{10,100,1000} etc) so that a single set of the recurring digits is now on the left of the decimal point.
- Subtract \textbf{x} from your answer to step 3. (Tip: Set this up like a column subtraction).
- Rearrange the resulting equation to give an answer for \textbf{x} as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers. Remember to simplify your answer when necessary.
Explain how to prove that a recurring decimal number is rational

Recurring decimal number examples
Example 6: proving that a recurring decimal is rational using algebra
Prove that 0.\dot{7}\dot{4} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify that the number is a recurring decimal.
0.\dot{7}\dot{4} is a recurring decimal where the set of digits ‘74’ is repeated after the decimal dot.
0.747474…
Write \bf{x =} the given number
Multiply \textbf{x} by a power of ten ( \bf{10,100,1000} etc) so that a single set of the recurring digits is now on the left of the decimal point.
There are two digits that repeat so we must multiply by 100.
100x= 74.747474...
Subtract \textbf{x} from your answer to step 3. (Tip: Set this up like a column subtraction).
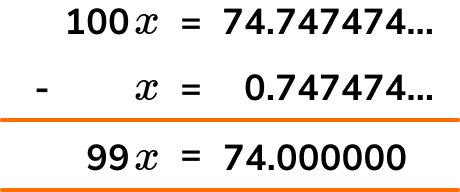
Rearrange the resulting equation to give an answer for \textbf{x} as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers. Remember to simplify your answer when necessary.
Example 7: proving that a recurring decimal is rational using algebra
Prove that 0.\dot{1}5\dot{3} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify that the number is a recurring decimal.
0.\dot{1}5\dot{3} is a recurring decimal where the set of digits ‘153’ is repeated after the decimal dot.
0.153153153…
Write \bf{x =} the given number
Multiply \textbf{x} by a power of ten ( \bf{10,100,1000} etc) so that a single set of the recurring digits is now on the left of the decimal point.
There are three digits that repeat so we must multiply by 1000.
1000x= 153.153153153...
Subtract \textbf{x} from your answer to step 3. (Tip: Set this up like a column subtraction).
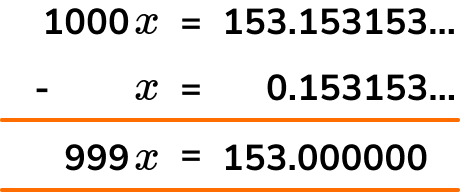
Rearrange the resulting equation to give an answer for \textbf{x} as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers. Remember to simplify your answer when necessary.
Example 8: proving that a recurring decimal is rational using algebra
Prove that 0.6\dot{4} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.
Identify that the number is a recurring decimal. This is a non-terminating decimal that repeats the same digit or same set of digits after the decimal point.
0.6\dot{4} is a recurring decimal. However after the decimal point there is the digit 6 that does not repeat and the digit 4 that does repeat. Because there is a non-repeating digit here this question requires some additional steps.
0.644444...
Write \bf{x =} the given number
Multiply \textbf{x} by a power of ten ( \bf{10,100,1000} etc) so that a single set of the recurring digits is now on the left of the decimal point.
First we multiply x by 10 to get the non repeating digit 6 to the left of the decimal point.
10x= 6.444444...
Then we multiply by 100 to get the repeating digit 4 to the left of the decimal point.
100x= 64.444444...
Subtract \textbf{x} from your answer to step 3. (Tip: Set this up like a column subtraction).
We now calculate 100x-10x
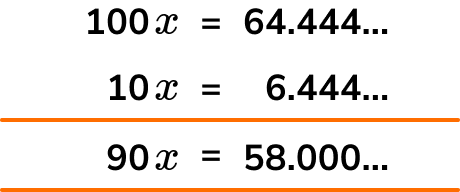
Rearrange the resulting equation to give an answer for \textbf{x} as a fraction in the form \bf{\frac{a}{b}} where \textbf{a} and \textbf{b} are integers. Remember to simplify your answer when necessary.
Common misconceptions
- Zero and rational numbers
Zero is a rational number because it can be written as \frac{0}{n} for any value of n other than 0.
- Fractions and rational numbers
All rational numbers can be written as fractions but not all fractions are rational numbers. If the fraction is in the form \frac{a}{b} , where a and b are integers, and b
For example,
\frac{\sqrt{2}}{3} is a fraction which is irrational.
- Non-terminating decimals and rational numbers
Some non-terminating decimals are irrational and others are rational.
For example,
\sqrt{3} =1.73205... \ \text{ This is a non terminating irrational number.}
\frac{7}{9} = 0.777... \ \text{ This is a non terminating rational number.}
Practice rational numbers questions
1. Which of the following numbers is not rational?




7 is an integer.
\frac{2}{7} is a fraction in the form \frac{a}{b} where a and b are integers.
0.2\dot{7} is a recurring decimal.
All of these are types of rational numbers.
\sqrt{27} = 5.196152… This is non terminating decimal which is not recurring and it cannot be expressed as a fraction in the form \frac{a}{b} where a and b are integers. It is therefore irrational.
2. Why is 0.\dot{7} a rational number?
Because it is a terminating decimal.

Because it is a non-terminating decimal.

Because it is a recurring decimal.

Because it is a non-recurring decimal.

0.\dot{7} is both a non-terminating decimal and a recurring decimal.
Not all non-terminating decimals are rational.
However all recurring decimals are rational because they can be expressed as fractions in the form \frac{a}{b} where a and b are integers.
Therefore this is the key fact in determining that 0.\dot{7} is rational.
3. Show that 3.5 is a rational number by expressing it as a fraction in the form \frac{p}{q} where p and q are integers.




4. Show that 0.\dot{8} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.




5. Which one of these numbers is a rational number that lies between 6.5 and 6\frac{2}{3} ?




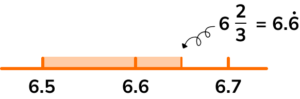
6.7 is rational but too big.
\sqrt{39.69} =6.3 is rational but too small.
\sqrt{43} =6.5574.. This number fits between the limits but is irrational.
6.\dot{5}=6.555… This number fits between the limits and is rational because it is a recurring decimal.
6. Show that 0.\dot{7}8\dot{3} is a rational number by expressing it as a fraction in the form \frac{a}{b} where a and b are integers.




Non-calculator
If all digits after the decimal dot are part of a recurring pattern then you can simply put those digits over the equivalent number of 9s and then simplify.
\frac{783}{999}=\frac{29}{37}
The proof is as follows.
\begin{aligned} x &=0.783 \\\\ x &=0.783783783 \ldots \\\\ 1000 x &=783.783783 \ldots \\\\ 1000 x-x &=783.783783 \ldots-0.783783 \ldots \\\\ 999 x &=783 \\\\ x &=\frac{783}{999}=\frac{29}{37} \end{aligned}
Calculator
\begin{aligned} &\frac{783}{1000}= 0.783 \\\\ &\frac{73}{99}= 0.737373…= 0.\dot{7}\dot{3} \\\\ &\frac{47}{60}= 0.78333…= 0.78\dot{3} \\\\ &\frac{29}{37}= 0.783783…= 0.\dot{7}8\dot{3} \end{aligned}
Rational numbers GCSE questions
1. Below is a list of numbers.
\frac{5}{6} \quad \quad \sqrt{2} \quad \quad 12 \quad \quad \frac{\pi}{5} \quad \quad -3.2 \quad \quad \frac{\sqrt{5}}{3}
Circle the three rational numbers.
(2 marks)
(2)
1 out of 2 marks for one correct answer
2 out of 2 marks for all three correct answers
2. (a) Judy says “five point six recurring is an irrational number because the decimal places go on forever”. Is Judy correct? Give a reason for your answer.
(b) State a rational number that lies between \sqrt{50} and 7.1
(3 marks)
(a)
No
(1)
Correct justification
(1)
Sample answers
No, Judy is not correct because 5.\dot{6} is a recurring decimal and all recurring decimals are rational.
No, Judy is not correct because 5.\dot{6} can be written as a fraction which shows that it is rational.
No, Judy is not correct because 5.\dot{6} can be written as the fraction 5\frac{2}{3} or \frac{17}{3} which shows that it is rational.
(b)
\sqrt{50} = 7.07106…
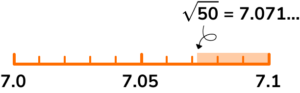
Any rational number that falls in the highlighted zone on this number line.
(1)
Possible answers include 7.076, \ 7.08, \ 7.09, \ 7.083, \ 7.95, \ 7.0\dot{7}, \ 7.0\dot{8}
3. Use an algebraic method to prove that 0.\dot{2}\dot{1} is a rational number by showing that it is equal to \frac{7}{33}.
(2 marks)
(1)
\begin{aligned} 99&x=21 \\\\ &x=\frac{21}{99} \\\\ &x=\frac{7}{33} \end{aligned}(1)
Learning checklist
You have now learned how to:
- Identify rational numbers
- Show that a number is rational by expressing it as a fraction in the form \frac{a}{b} where a and b are integers and b ≠ 0
- Prove that a recurring decimal is rational using algebra
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.