High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Fractions Decimals Multiplying and dividing integers Coordinate planeWhat is a proportion in math
Here you will learn what a proportion is, including what direct and inverse proportions are and how to solve problems with them.
Students will first learn about proportions in math as part of ratios and proportions in 7 th grade.
What is a proportion in math?
A proportion in math expresses the equivalence of two ratios.
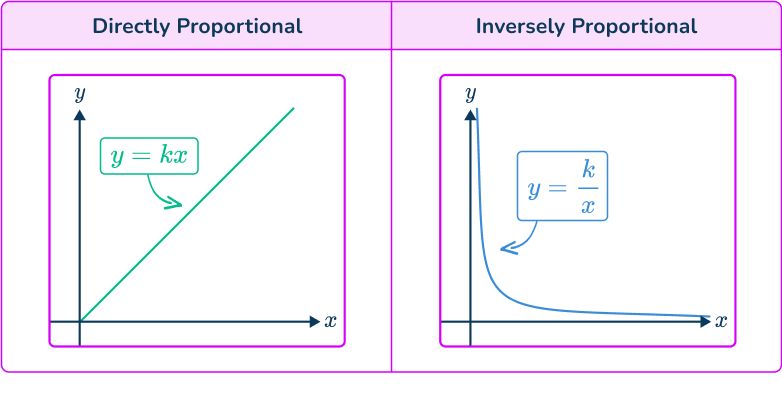
A direct proportion in math is represented by the equation y=kx.
This means that y is proportional to x. \, k is a constant value that links the two variables, called the constant of proportionality.
When y increases as x increases, the proportion is called a direction variation or direct proportion.
For example,
If k=2 then y would be double the value of x for every value of x.
Direct proportions are seen in many real life situations such as exchange rates, converting between units, and the price of something per dollar.
Step-by-step guide: Direction variation equation
Step-by-step guide: Directly proportional
Step-by-step guide: Direction variation
Inverse proportionality describes a relationship between x and y where an increase in x results in a decrease in y.
For example, the time taken to paint a house is inversely proportional to the number of workers. As the number of workers increases, the painting time decreases.
An inverse proportion in math is represented by the equation y=\cfrac{k}{x}, where the numerator k is the constant of proportionality and the denominator x is the independent variable.
Step-by-step guide: Direct and inverse variation
Step-by-step guide: Inversely proportional
Step-by-step guide: Inverse proportion formula
Proportional relationships can be graphed. When graphing the equation y=kx, where k is a constant, the graph is a straight line passing through the origin.
However, when we consider the reciprocal function y=\cfrac{k}{x}, the relationship between y and x becomes inverse.
As x increases, the value of y decreases. This results in a curved graph that does not pass through the origin nor intersects either axis.
Step-by-step guide: Directly proportional graph
What is a proportion in math?

Common Core State Standards
How does this relate to 7 th grade math?
- Grade 7 – Ratios and Proportional Relationships (7.RP.A.2)
Recognize and represent proportional relationships between quantities.
a. Decide whether two quantities are in a proportional relationship, for example, by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
b. Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.
c. Represent proportional relationships by equations. For example, if the total cost t is proportional to the number of items n purchased at a constant price p, the relationship between the total cost and the number of items can be expressed as t=pn.
d. Explain what a point (x, \, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, \, 0) and (1, \, r) where r is the unit rate.
- Grade 7 – Ratios and Proportional Relationships (7.RP.A.2b)
Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.
- Grade 8 – Expressions and Equations (8.EE.B.5)
Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways.
- High School – Functions – Interpreting Functions (HS.F.IF.B.4)
For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
[FREE] Ratio Worksheet (Grade 6 to 7)
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of ratios and proportions. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
[FREE] Ratio Worksheet (Grade 6 to 7)
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of ratios and proportions. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!
DOWNLOAD FREEHow to solve problems with a proportion in math
There are a lot of ways to solve problems with a proportion in math. For more specific step-by-step guides, check out the pages linked in the “What is a proportion in math?” section above or read through the examples below.
What is a proportion in math examples
Example 1: write a proportional equation
If x and y vary directly, write the direct variation equation when x=6 and y=15.
- Calculate the constant of variation, \textbf{k}.
To calculate k, use the direct variation equation, y=kx.
y=kx can also be written as k=\cfrac{y}{x}.
Substitute in 6 for x and 15 for y to calculate k.
\begin{aligned}& k=\cfrac{y}{x}=\cfrac{15}{6}=2.5 \\\\ & k=2.5 \end{aligned}The constant of variation k is 2.5.
2Write the equation in the form of \textbf{y } \bf{ = } \textbf{ kx}.
The direct variation equation can be written by substituting 2.5 in for k.
y=2.5xExample 2: unknown variable in a proportion table
Given that y is directly proportional to x, calculate the value for y when x=11.

Write down the direct proportion formula.
Since y is directly proportional to x, you can use the formula y=kx.
Determine the value of \textbf{k}.
From the table, you can see that when x=6, \, y=4.5. By substituting these values into the formula, you get the value of k.
\begin{aligned}& 4.5=k \times 6 \\\\
& 4.5 \div 6=k \\\\
& 0.75=k \end{aligned}
Substitute \textbf{k} and the known value into the direct proportion formula.
Substituting k=0.75 into the formula, you have:
y=0.75x
To find the value for y when x=11, substitute x=11 into the equation.
y=0.75 \times 11
Solve the equation.
Example 3: find the constant of variation from a graph
Use the graph to find the constant of variation.
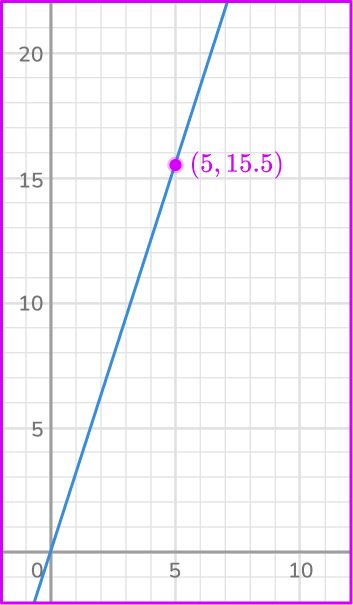
Select a point.
Use the point (5, \, 15.5).
Write the point as a ratio in the form of \cfrac{\textbf{y}}{\textbf{x}}.
Write the value of \textbf{k}.
Example 4: complete the table y ∝ 1/x
Let y\propto\cfrac{1}{x}. Calculate the value for x when y=2.

Write down the inverse proportion formula.
As y\propto\cfrac{1}{x} as stated in the question, you have:
y=\cfrac{k}{x}
Determine the value of \textbf{k}.
As x=2 when y=10, substituting these values into the formula, you get:
\begin{aligned}& 10=\cfrac{k}{2} \\\\
& 10 \times 2=k \\\\
& k=20 \end{aligned}
Substitute \textbf{k} and the known value into the inverse proportion formula.
Now you have y=\cfrac{20}{x}. You need to determine the value for x when y=2 and so, substituting this value into the equation, you get:
2=\cfrac{20}{x}
Solve the equation.
Example 5: determine the inverse proportion formula when y ∝ 1/x
Let y be inversely proportional to x. When y=\cfrac{1}{2}, \, x=12. By calculating the constant of proportionality, determine a formula for y in terms of x.
Write down the inverse proportion formula.
Since y is inversely proportional to x, \, y=\cfrac{k}{x} where k is the constant of proportionality.
Determine the value of \textbf{k}.
Substitute in the values you were given to find the constant of proportionality.
\begin{aligned}& y=\cfrac{k}{x} \\\\
& \cfrac{1}{2}=\cfrac{k}{12} \\\\
& k=12 \times \cfrac{1}{2}=6 \end{aligned}
Substitute \textbf{k} into the inverse proportion formula.
Since k=6, the inverse proportion formula is y=\cfrac{6}{x}.
Example 6: using a directly proportional graph
The graph shows the relationship between the US Dollar and Mexican Pesos. Use the graph to estimate the number of US Dollars there are for 200 Mexican Pesos.
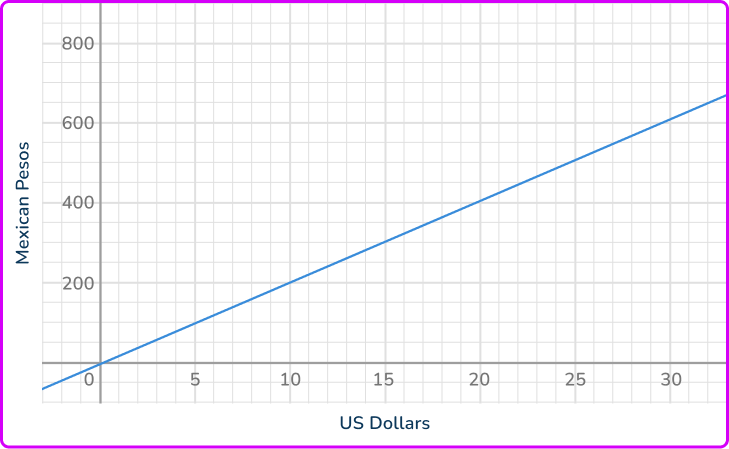
Locate the value on the correct axis.
You have been given the value 200 Mexican Pesos, so you need to locate this value on the vertical axis.
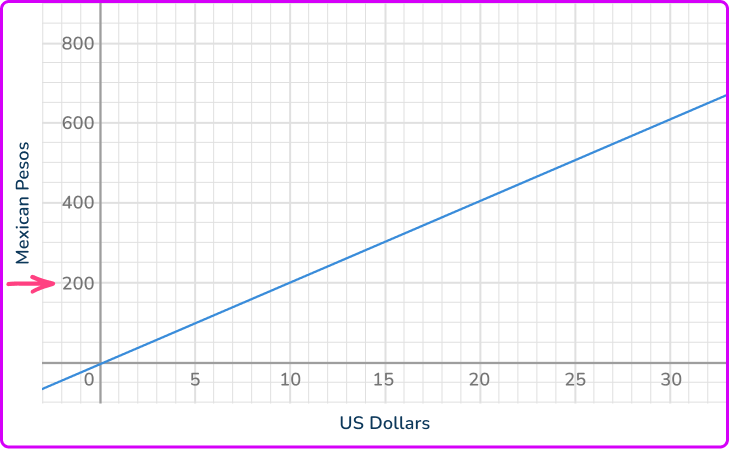
Use straight lines to find the corresponding value from the other axis.
Draw a straight line across the graph and then another straight line down to the other axis.
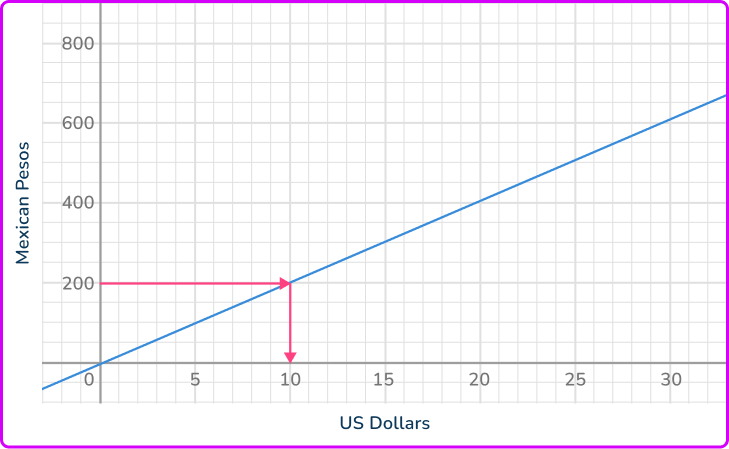
Read off the corresponding value from the other axis.
Looking at the horizontal axis, the value you need is approximately 10.
200 Mexican Pesos is worth approximately 10 US Dollars.
Teaching tips for what is a proportion in math
- Before teaching and solving proportions, review topics such as equivalent fractions, how to simplify fractions or a given ratio.
- Start with whole numbers before moving on to integers and fractional numbers in proportion problems.
- Choose worksheets that have different types of proportions shown in different ways, including word problems, real-life conversion, and continued proportions.
Easy mistakes to make
- Incorrectly using cross multiplication
The cross multiply strategy can be useful in certain instances if students understand why it works. It is important for students to have enough meaningful experiences with proportions to develop an understanding of all properties of proportions.
Conversely, when students do not understand why the cross products strategy works, they can make mistakes such as multiplying only one side of the equation or writing the proportion formula down incorrectly.
- Thinking proportions only increase
Since students are typically first introduced to direct proportions, this is understandable. As students advance in their understanding of inverse proportions, students are exposed to the decrease and can update this line of thinking.
- Substituting the \textbf{x} -coordinate and \textbf{y} -coordinate incorrectly
When you are given a point and need to find the equation of direct variation, substitute the x -coordinate in for the x value and the y -coordinate for the y -value.
For example, (5, \, 3)
Practice what is a proportion in math questions
1. Which of the following proportions is not equivalent to the others?




Reduce each proportion to its simplest form, then compare.
\cfrac{32 \div 8}{40 \div 8}=\cfrac{4}{5}
\cfrac{9 \div 3}{15 \div 3}=\cfrac{3}{5}
\cfrac{48 \div 12}{60 \div 12}=\cfrac{4}{5}
\cfrac{24 \div 6}{30 \div 6}=\cfrac{4}{5}
2. Which of these equations does NOT represent a direct variation?




Direct variation equations are in the form of y=kx. There can be no addition or subtraction involved in the equation. The only equation that is not in that form is y=x-2.
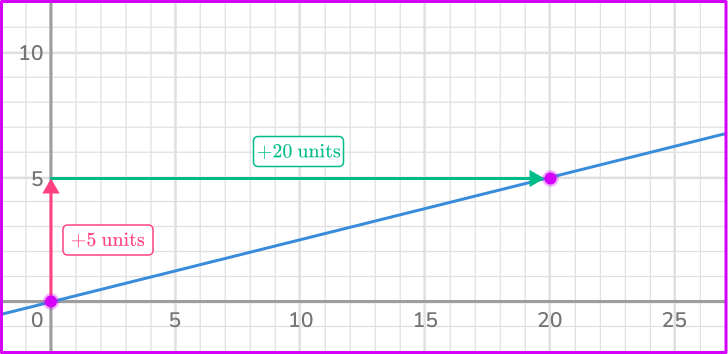
3. What is the constant of variation from the graph?
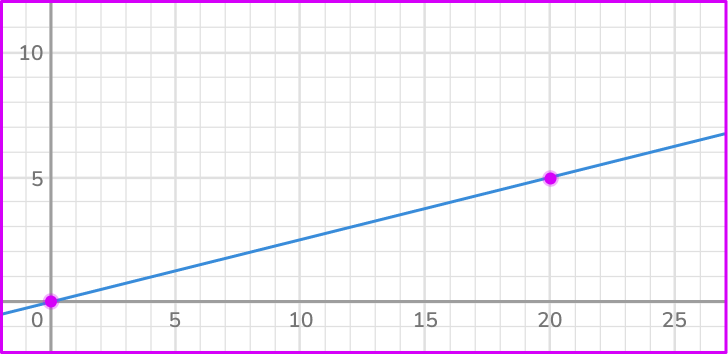




From the graph, you can see that the line passes through (0, \, 0) and (20, \, 5). Using the point (20, \, 5), the ratio of the point in the form of \cfrac{y}{x} is \cfrac{5}{20} or \cfrac{1}{4}.
4. As y is inversely proportional to x, complete the table by calculating the missing value for y.
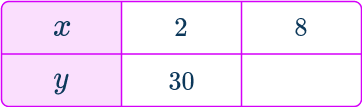




y=\cfrac{k}{x} and so k=xy.
k=2\times{30}=60
y=\cfrac{60}{x}
When x=8, \, y=\cfrac{60}{8}=7.5
5. y is inversely proportional to x.
When y=6.25, \, x=4.
Write a formula for y in terms of x.




Write down the relationship between y and x and substitute the given values to find k, the constant of proportionality.
As y\propto\cfrac{1}{x} and so y=\cfrac{k}{x}.
As y=6.25 when x=4,
\begin{aligned}& 6.25=\cfrac{k}{4} \\\\ & k=4 \times 6.25=25 \end{aligned}
So the equation is y=\cfrac{25}{x}.
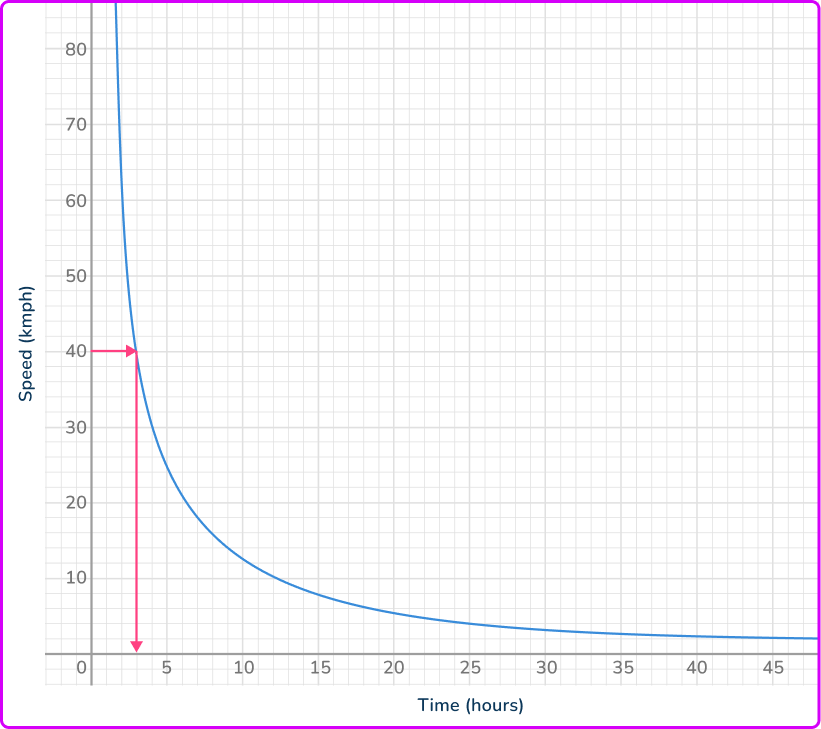
6. The graph shows the relationship between speed and time of a journey. Find the time taken for the journey when the speed is 40\mathrm{~km/h}.
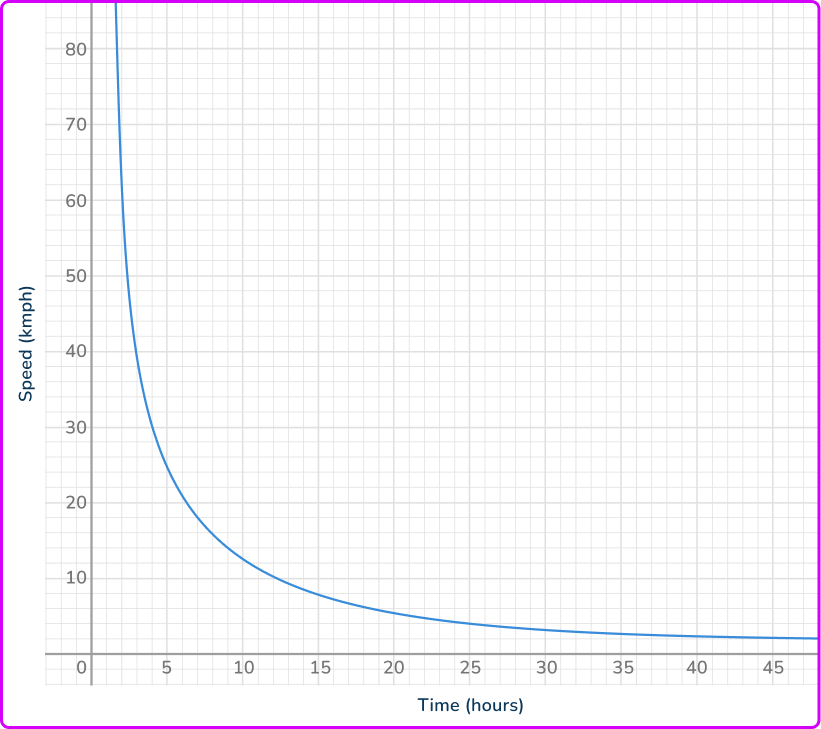
5 hours

4 hours

6 hours

3 hours

Find 40\mathrm{~km/h} on the vertical axis. Draw a horizontal line across the graph, and then a vertical line down to the other axis. Read off the value from the horizontal axis.
What is a proportion in math FAQs
This symbol is used to show that two ratios are equivalent.
A mathematical statement that shows two ratios who are equal to each other.
A direct proportion is a specific type of linear equation that passes through (0, \, 0).
A quadratic equation is a polynomial equation of degree 2, where the total number of terms can vary but always includes a term with the variable squared (which is also the highest exponent value).
The next lessons are
- Converting fractions decimals and percentages
- Percent
- Compound measure
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!