Constant of Proportionality - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Simplifying fractions Equivalent fractions Factors Ratio

Math resources Ratio and proportion Ratio

Constant of proportionality

Here you will learn about the constant of proportionality, including what it is and how to identify it in graphs, tables and verbal descriptions.

Students will first learn about the constant of proportionality as part of ratios and proportions in $7$ th grade.

What is the constant of proportionality?

The constant of proportionality defines the relationship between the independent, $x,$ and dependent, $y,$ variables in a proportional relationship.

For example,

The table shows a proportional relationship.

How do you know the relationship is proportional?

Look at how $y$ relates to the corresponding $x$ values… $y$ is always half the value of $x.$

The relationship between $x$ and $y$ is constant and can be represented by a multiplicative relationship:

\begin{aligned}& 8 \times \cfrac{1}{2}=4 \\\\ & 14 \times \cfrac{1}{2}=7 \\\\ & 7 \times \cfrac{1}{2}=3.5 \\\\ & 9 \times \cfrac{1}{2}=4.5 \\\\ & 10 \times \cfrac{1}{2}=5 \end{aligned}

The constant of proportionality is $\cfrac{1}{2},$ because it defines the multiplicative relationship between $x$ and $y.$

The proportionality equation for this specific relationship is $\cfrac{1}{2} \, x=y.$

Below, the unit rate is calculated for each ordered pair in the relationship:

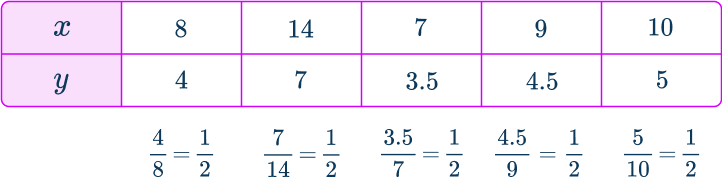
Notice, the unit rate is the same as the constant of proportionality.

The letter $k$ is often used to represent the constant of proportionality so here, $k=\cfrac{1}{2}.$

Note: Only directly proportional relationships are covered on this page.

Step-by-step guide: Inversely proportional

What is the constant of proportionality?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7 – Ratios and Proportions (7.RP.A.2b)
Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.

[FREE] Ratio Worksheet (Grade 6 to 7)

Teaching constant of proportionality? Use this quiz to check your grade 6 to 7 students’ understanding of ratios and constant of proportionality. 10+ questions with answers covering a range of ratio topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Ratio Worksheet (Grade 6 to 7)

DOWNLOAD FREE

How to identify the constant of proportionality

In order to identify the constant of proportionality:

Confirm that the relationship is proportional.
Identify a coordinate $\textbf{(x, y)}$ in the proportion.
Calculate the unit rate of the proportion.

Constant of proportionality examples

Example 1: find k using a graph

The graph shows the number of miles a drone traveled after some hours. What is the constant of proportionality?

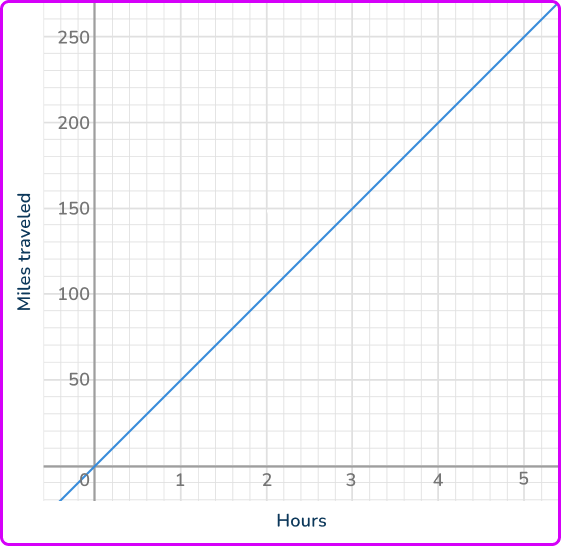
Confirm that the relationship is proportional.

The graph of the relationship is a direct proportion, because the graph is a straight line that passes through the origin.

2Identify a coordinate $\textbf{(x, y)}$ in the proportion.

There are $6$ coordinates that are easy to identify:

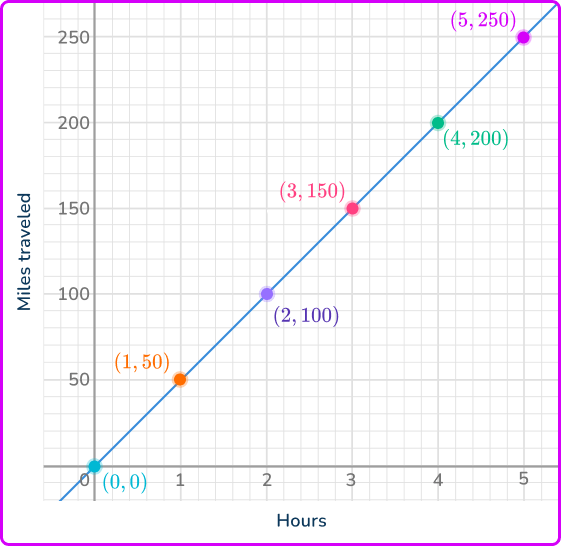
3Calculate the unit rate of the proportion.

You can use any coordinate, except $(0, \, 0),$ to calculate the unit rate.

\cfrac{50 \text { miles }}{1 \text { hour }}=50 \mathrm{~mph}

The constant of proportionality is $50\mathrm{~mph}.$ This means $y$ is always $50$ times the size of $x.$ Since the relationship is a direct proportion, this will be true for any $(x, \, y).$

To check your work, confirm this by calculating with $k$ for the other ordered pairs.

\begin{aligned}& 50 \mathrm{~mph} \times 2 \text { hours }=100 \text { miles } \\\\ & 50 \mathrm{~mph} \times 3 \text { hours }=150 \text { miles } \\\\ & 50 \mathrm{~mph} \times 4 \text { hours }=200 \text { miles } \\\\ & 50 \mathrm{~mph} \times 5 \text { hours }=250 \text { miles } \end{aligned}

Example 2: find k using a table

The table shows the number of hours it takes to make some batches of cookies. What is the constant of proportionality?

Confirm that the relationship is proportional.

If the relationship is proportional, then each batch of cookies takes the same number of hours to make. This won’t be known until we know the unit rate for each – so we’ll revisit this part in Step $3.$

Identify a coordinate $\textbf{(x, y)}$ in the proportion.

The table gives us $4$ coordinates:

$\begin{aligned}& (3, \, 4) \\\\ &(6, \, 8) \\\\ &(9, \, 12) \\\\ &(10, \, 13 \frac{1}{3}) \end{aligned}$

In this case, the ‘number of batches’ as $x,$ means the ‘number of hours’ will depend on how many batches are made.

Calculate the unit rate of the proportion.

We will calculate the unit rate for all coordinates, to ensure that the relationship is proportional.

$\frac{4\text{ hours }}{3\text{ batches }}=1 \frac{1}{3}\text{ hours per batch}$

$\frac{8\text{ hours }}{6\text{ batches }}=1 \frac{1}{3}\text{ hours per batch}$

$\frac{12\text{ hours }}{9\text{ batches }}=1 \frac{1}{3}\text{ hours per batch}$

$\frac{13\frac{1}{3}\text{ hours }}{10\text{ batches }}=1 \frac{1}{3}\text{ hours per batch}$

The constant of proportionality is $1\frac{1}{3}$ hours per batch. This means that $y$ will always be $1\frac{1}{3}$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

Example 3: find k using a description

Quinn is reading chapters of a book at a constant rate. Quinn finishes $5$ chapters in $2$ days. What is the constant of proportionality?

Confirm that the relationship is proportional.

At $0$ days Quinn had read $0$ chapters and Quinn’s rate of reading is constant, making the relationship proportional.

Identify a coordinate $\textbf{(x, y)}$ in the proportion.

In $2$ days, Quinn reads $5$ chapters, represented by the coordinate $(2, \, 5).$ The days are the independent variable $x,$ since the number of chapters finished will depend on how many days Quinn has been reading.

Calculate the unit rate of the proportion.

$\cfrac{5 \text { chapters }}{2 \text { days }}=2.5$ chapters per day

The constant of proportionality is $2.5$ chapters per day. This means that $y$ will always be $2.5$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

Example 4: find k using a graph

The graph shows the number of kilometers a train traveled after some hours. What is the constant of proportionality?

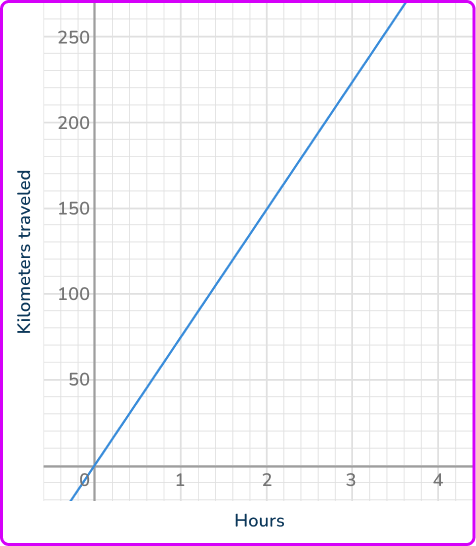
Confirm that the relationship is proportional.

The graph of the relationship is a direct proportion, because the graph is a straight line that passes through the origin.

Identify a coordinate $\textbf{(x, y)}$ in the proportion.

There are $2$ coordinates that are easy to identify:

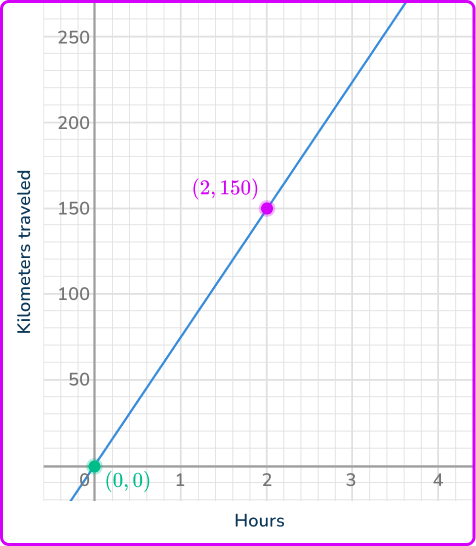
Calculate the unit rate of the proportion.

You can use any coordinate, except $(0, \, 0),$ to calculate the unit rate.

$\cfrac{150 \text { kilometers }}{2 \text { hours }}=75 \mathrm{~kph}$

The constant of proportionality is $75\mathrm{~kph}.$ The value of $y$ will always be $75$ times the size of $x.$ Since the relationship is a direct proportion, this will be true for any $(x, \, y).$

Example 5: find k using a table

The table shows the ratio of white paint to red paint is $5\text{:}9.$ What is the constant of proportionality?

Confirm that the relationship is proportional.

All ratios are proportional relationships.

Identify a coordinate $\textbf{(x, y)}$ in the proportion.

The table gives us $4$ coordinates:

$\begin{aligned}&(5, \, 9) \\\\ &(10, \, 18) \\\\ &(20, \, 36) \\\\ &(15, \, 27) \end{aligned}$

Calculate the unit rate of the proportion.

You can use any coordinate to calculate the unit rate.

$\cfrac{9\text { ounces of red paint }}{5\text { ounces of white paint }}=1.8$ ounces of red paint per ounce of white paint

The constant of proportionality is $1.8$ ounces of red paint per ounce of white paint. This means $y$ is always $1.8$ times the size of $x.$ Since the relationship is a direct proportion, this will be true for any $(x, \, y).$ To check your work, confirm this by calculating with $k$ for the other ordered pairs.

$\begin{aligned}& 10 \text { ounces } \times 1.8=18 \text { ounces } \\\\ & 20 \text { ounces } \times 1.8=36 \text { ounces } \\\\ & 15 \text { ounces } \times 1.8=27 \text { ounces } \end{aligned}$

Example 6: find k using a description

On a map, every $4$ inches represents $240$ miles. What is the constant of proportionality?

Confirm that the relationship is proportional.

The scale of a map is the relationship between the actual distances and what is shown on the map. This relationship is always constant, making it a proportional relationship.

Identify a coordinate $\textbf{(x, y)}$ in the proportion.

On the map $4$ inches is $240$ miles, represented by the coordinate $(4, \, 240).$ In this case either variable could be independent, but we define the inches on the map as $x,$ so the constant of proportionality will show the relationship from inches to miles.

Calculate the unit rate of the proportion.

\cfrac{240 \text { miles }}{4 \text { inches }}=60 \text { miles per inch }

The constant of proportionality is $60$ miles per inch. $y$ will always be $60$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

Teaching tips for constant of proportionality

Before finding the constant of proportionality, review ratios and the operations of multiplication and division.

Make connections to the constant of proportionality beyond just a math class setting. For example, challenge students to think of as many real world proposition examples as possible (such as the price of gallons of gas, apples per pound, the conversion of reward points to dollars in an app, etc.).

Choose activities, worksheets and quizzes that expose students proportions in different formats and with a variety of proportional quantity types (whole numbers, fractions, decimals, etc.).

Use precise vocabulary and do not introduce advanced topics unnecessarily. For example, students are introduced to the constant of proportionality before they are taught what the slope of a line or rate of change is, so avoid using these terms until they have been formally introduced.

Provide a link to a proportionality calculator for struggling students to check their work or see more worked examples.

Easy mistakes to make

Confusing which is the $\textbf{x}$ -value and $\textbf{y}$ -value in proportional relationships
Students confuse $x$ -values and $y$ -values in proportional relationships due to misinterpreting their roles or reversing their meanings – particularly when the independent and dependent variables are not explicitly defined in a problem.

To avoid this, encourage students to clarify the context of the variables, label axes and tables clearly, and emphasize the dependent and independent relationship.

Using the wrong value for the numerator or denominator
For example,
In Example $6,$ students may write the equation as
$\cfrac{4 \text { inches }}{240 \text { miles }}=\cfrac{1}{60} \text { miles per inch }$

There are a few ways to avoid this. Firstly, always have students include the units, so they can catch this mistake. What is really calculated above is the “inches per mile” not “miles per inches”.

Secondly, have students use their calculated constant of proportionality to convert between $x$ and $y,$ to confirm that they did not make a mistake. In this case $4 \times \cfrac{1}{60}$ ≠ $240.$

Practice constant of proportionality questions

4

5

0.5

3.5

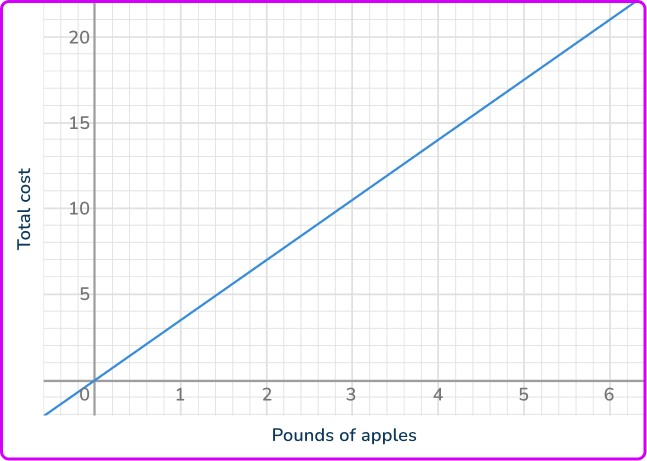
The graph of the relationship is a proportion, because the graph is a straight line that passes through the origin.

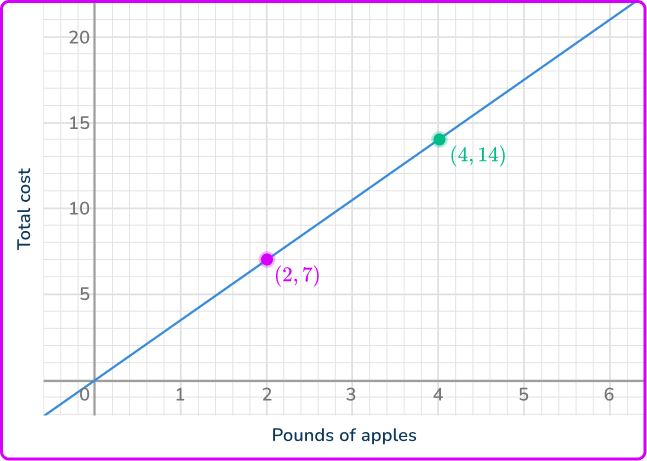
Constant of proportionality 10 US

You can use any coordinate, except $(0, \, 0),$ to calculate the unit rate.

\cfrac{\$ 7}{2 \text { pounds }}=\$ 3.50 \text { per pound }

The constant of proportionality is $\$ 3.50$ per pound. This means y is always $3.5$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$ To check your work, confirm this by calculating with $k$ for the other ordered pairs.

4 \text { pounds } \times \$ 3.50=\$ 14

17

51

\cfrac{1}{17}

3

If the relationship is proportional, then each mile driven uses the same amount of gas.

The table gives us $4$ coordinates:

\begin{aligned}&(3, \, 51) \\\\ &(5, \, 85) \\\\ &(6, \, 102) \\\\ &(10, \, 170) \end{aligned}

We will calculate the unit rate for all coordinates, to ensure that the relationship is proportional.

\begin{aligned}& \cfrac{51 \text { miles }}{3 \text { gallons }}=17 \text { miles per gallon } \\\\ & \cfrac{85 \text { miles }}{5 \text { gallons }}=17 \text { miles per gallon } \\\\ & \cfrac{102 \text { miles }}{6 \text { gallons }}=17 \text { miles per gallon } \\\\ & \cfrac{170 \text { miles }}{10 \text { gallons }}=17 \text { miles per gallon } \end{aligned}

The constant of proportionality is $17$ miles per gallon. This means that $y$ will always be $17$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

\cfrac{1}{4}

4

3

12

At $0$ hours Andela had filled $0$ jars and Andela’s rate of filling jars is constant, making the relationship proportional.

In $3$ hours, Andela fills $12$ jars, represented by the coordinate $(3, \, 12).$ The hours are the independent variable $x,$ since the number of jars filled will depend on how many hours Andela has been working.

\cfrac{12 \text { jars }}{3 \text { hours }}=4 \text { jars per hour }

The constant of proportionality is $4$ jars per hour. This means that $y$ will always be $4$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

10

2

11

20

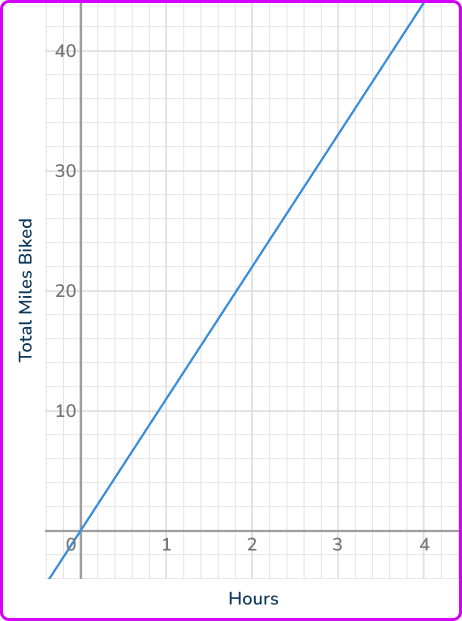
The graph of the relationship is a proportion, because the graph is a straight line that passes through the origin.

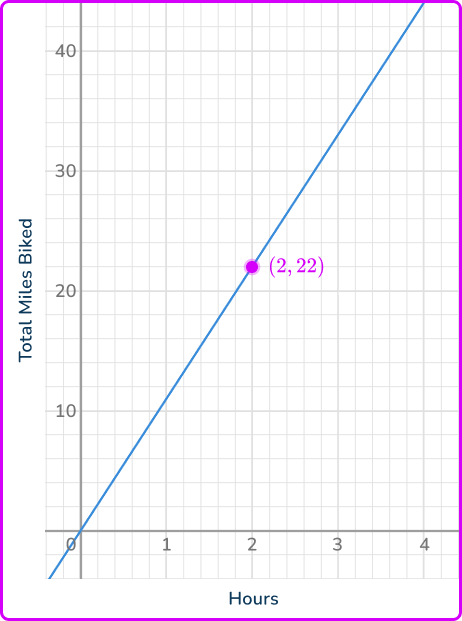
Constant of proportionality 13 US

Use the coordinate $(2, 22)$ to calculate the unit rate.

\cfrac{22 \text { miles }}{2 \text { hours }}=11 \text { miles per hour }

The constant of proportionality is $11$ miles per hour. This means $y$ is always $11$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

0.8

1.25

1

4

If the relationship is proportional, then the unit rate of cups of blueberries to $1$ cup of pineapple is always the same.

The table gives us $4$ coordinates:

\begin{aligned}&(4, \, 5) \\\\ &(5, \, 6.25) \\\\ &(7, \, 8.75) \\\\ &(8, \, 10) \end{aligned}

We will calculate the unit rate for all coordinates, to ensure that the relationship is proportional.

\begin{aligned}& \cfrac{5 \text { cups of pineapple }}{4 \text { cups of blueberries }}=1.25 \text { cups of pineapple per } 1 \text { cup of blueberries } \\\\ & \cfrac{6.25 \text { cups of pineapple }}{5 \text { cups of blueberries }}=1.25 \text { cups of pineapple per } 1 \text { cup of blueberries } \\\\ & \cfrac{8.75 \text { cups of pineapple }}{7 \text { cups of blueberries }}=1.25 \text { cups of pineapple per } 1 \text { cup of blueberries } \\\\ & \cfrac{10 \text { cups of pineapple }}{8 \text { cuns of blueberries }}=1.25 \text { cups of pineapple per } 1 \text { cup of blueberries } \end{aligned}

The constant of proportionality is $1.25$ cups of pineapple per $1$ cup of blueberries. This means that $y$ will always be $1.25$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

0.04

50

4

25

At $0$ hours the machine has made $0$ cans and the machine’s rate is constant, making the relationship proportional.

In $3$ hours, the machine makes $75$ cans, represented by the coordinates $(3, \, 75).$ The hours are the independent variable $x,$ since the number of cans made will depend on how many hours the machine has been working.

\cfrac{75 \text { cans }}{3 \text { hours }}=25 \text { cans per hour }

The constant of proportionality is $25$ cans per hour. This means that $y$ will always be $25$ times the size of $x.$ Since the relationship is a proportion, this will be true for any $(x, \, y).$

Constant of proportionality FAQs

How do students use this skill in $\bf{8}$ th grade and in high school?

After learning about proportions, students extend this knowledge to understand linear equations and functions – which is started in $8$ th grade and continued into high school.

What is the proportionality formula?

$y=kx,$ where $k$ is the constant of proportionality.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.