High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Properties of equality
Here you will learn about the properties of equality, including what they are and how to use them to solve problems.
Students will first learn about the properties of equality as part of operations and algebraic thinking in 3rd grade and continue to build on this knowledge in operations and algebraic thinking in 5th grade and expressions and equations in 6th grade.
What are properties of equality?
Properties of equality are general rules that can be applied to an equation to create equivalent equations, which can be useful when comparing or solving equations.
The associative property states that numbers can be grouped in different ways when they are added or multiplied and the answer will stay the same.
For example,
When adding 7 + 8 + 10, the addends can be grouped in different ways:
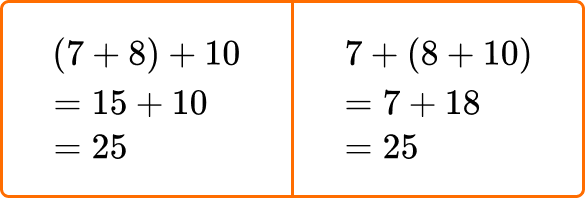
For example,
When multiplying 4 \times 6 \times 2, the numbers can be grouped in different ways:
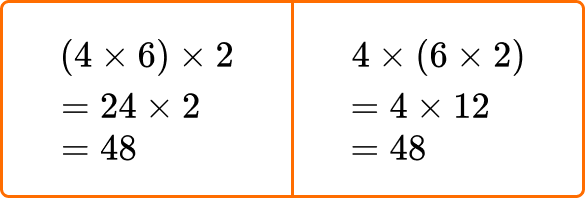
The associative property works for both addition and multiplication, because it creates equivalent equations.
(4 \times 6) \times 2=4 \times(6 \times 2) \quad and \quad (7+8)+10=7+(8+10)
Step-by-step guide: Associative property
The commutative property states that the order of numbers can be changed when they are added or multiplied and the answer will stay the same.
For example,
When adding 11 + 15, you can change the order of the addends:
For example,
When multiplying 6 \times 5, you can change the order of the numbers:
Notice that even with a different order, the sum and the product are the same.
Step-by-step guide: Commutative property
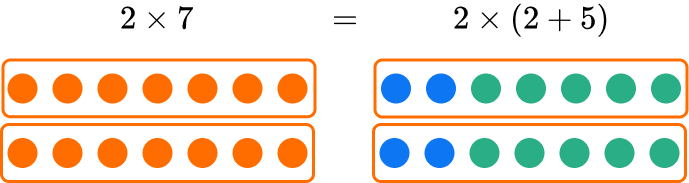
The distributive property says that multiplying the sum of two or more numbers is equivalent to separately multiplying the addends.
For example,
When multiplying 2 \times 7, you can break 7 up into 2 + 5.
The distributive property allows us to multiply each part and then add the products together.
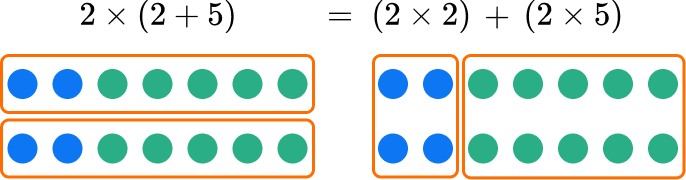
Any way you solve the equivalent expressions, the product is the same.
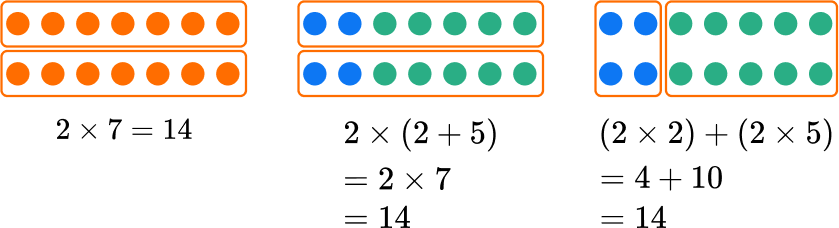
Initially, the distributive property is used to think flexibly about numbers. In later grades, students learn to simplify algebraic expressions using the distributive property.
Step-by-step guide: Distributive property
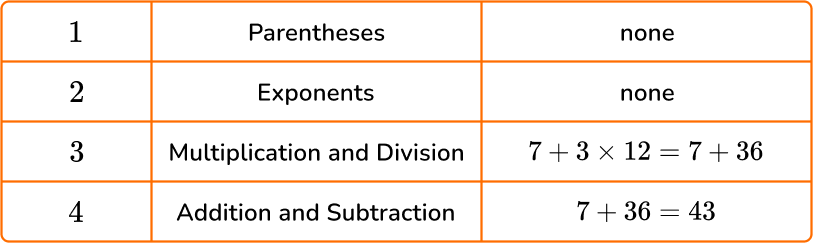
Order of operations is the sequence of steps followed to evaluate an expression.
All the mathematical operations must be completed in a specific order, following the acronym PEMDAS.
PEMDAS stands for:
Parentheses, Exponents, Multiplication and Division, Addition and Subtraction
The operations of multiplication and division are given equal priority, and addition and subtraction are also given equal priority.
Always solve these operations starting from the left side and working to the right side, unless there are parentheses.
For example,
Step-by-step guide: Order of operations
What are properties of equality?
![[FREE] Properties of Equality Worksheet (Grade 3 to 6)](https://thirdspacelearning.com/wp-content/uploads/2023/07/properties-of-equality-check-for-understanding-quiz-listing-image-.png)
[FREE] Properties of Equality Worksheet (Grade 3 to 6)
Use this quiz to check your grade 3 to 6 students’ understanding of properties of equality. 10+ questions with answers covering properties of equality topics to identify learning gaps!
DOWNLOAD FREE [FREE] Properties of Equality Worksheet (Grade 3 to 6)
Use this quiz to check your grade 3 to 6 students’ understanding of properties of equality. 10+ questions with answers covering properties of equality topics to identify learning gaps!
DOWNLOAD FREECommon Core State Standards
How does this relate to 3rd grade math, 5th grade math, and 6th grade math?
- Grade 3 – Operations and Algebraic Thinking (3.OA.B.5)
Apply properties of operations as strategies to multiply and divide.
Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication.)
3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication.)
Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Properties of equality.)
- Grade 5 – Operations and Algebraic Thinking (5.OA.1)
Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.
- Grade 5 – Operations and Algebraic Thinking (5.OA.2)
Write simple expressions that record calculations with numbers, and interpret numerical expressions without evaluating them.
- Grade 6 – Expressions and Equations (6.EE.1)
Write and evaluate numerical expressions involving whole-number exponents.
How to use properties of equality
There are a lot of ways to use properties of equalities. For more specific step-by-step guides, check out the individual pages linked in the “What are properties of equalities?” section above or read through the examples below.
Properties of equality examples
Example 1: simple associative property with addition
Use the associative property to solve 17 + 6 + 34.
- Check to see that the operation is addition or multiplication.
The associative property can be used since all the numbers are being added.
2Change the grouping of the numbers and solve.
\begin{aligned} & 17+6+34 \\\\ & =17+(6+34) \quad \text{ *Group and add these numbers first} \\\\ & =17+40 \\\\ & =57 \end{aligned}
Example 2: associative property – addition with friendly numbers
Use the associative property with friendly numbers to solve 77 + 16.
Check to see that the operation is addition or multiplication.
The associative property can be used, since all the numbers are being added.
Change the grouping of the numbers and solve.
\begin{aligned} & 77+16 \\\\ & =77+(3+13) \quad \text{ *Break apart } 16 \\\\ & =(77+3)+13 \quad \text{*Regroup and add these numbers first} \\\\ & =80+13 \quad \quad \;\;\; \text{ *80 is a friendly number because it is a multiple of } 10 \\\\ & =93 \end{aligned}
Notice that friendly numbers can be multiples of 10, because they are easier to add mentally.
Example 3: commutative property – multiplication with friendly numbers
Use the commutative property to create a friendly number and solve 3 \times 9 \times 2.
Check to see that the operation is addition or multiplication.
The commutative property can be used, since all the numbers are being multiplied.
Change the order of the numbers and solve.
\begin{aligned} & 3 \times 9 \times 2 \\\\ & =3 \times 2 \times 9 \quad \text{ *Change the order of the 9 and 2 }\\\\ & =6 \times 9 \quad \quad \; \text{ *Multiplying 3 and 2 creates 6} \\ &\quad \quad \quad \quad \quad \;\; \text{ - a single digit number easier to multiply }\\ & =54 \end{aligned}
Notice that when multiplying, friendly numbers can be single digit numbers.
If you know your basic facts, it is easier to solve 6 \times 9 than solving 3 \times 9 \times 2=27 \times 2.
Example 4: distributive property with basic facts
Show how to solve 8 \times 11 using the distributive property.
Identify an equation multiplying two numbers.
You can use the distributive property with 8 \times 11, since it is multiplication.
Show one of the numbers being multiplied as a sum of numbers.
Either 8 or 11 can be shown as a sum, but for this example let’s break up 8 into 5 + 3.
8 \times 11=(5+3) \times 11
Multiply each number in the sum.
\begin{aligned} & (5+3) \times 11 \\\\ & =(5 \, \times \, 11)+(3 \times 11) \\\\ & =55+33 \end{aligned}
Add the partial products together to find the final product.
55 + 33 = 88
8 \times 11=88 can be solved using the distributive property.
Example 5: PEMDAS with division and subtraction
Evaluate 40-8 \div 4.
Solve any calculations within parentheses.
There are no parentheses.
Solve for any exponents.
There are no exponents.
Solve any division and multiplication calculations.
The division you need to calculate is 8 \div 4=2.
Replacing 8\div{4} with 2 gives us the calculation 40-2.
Solve any addition and subtraction calculations.
40-2=38
So, 40-8 \div 4=38.
Example 6: PEMDAS with brackets, an exponent, and division
Evaluate 12+(16 \, \div \, 4 \times 5)^2.
Solve any calculations within parentheses.
Within the set of parentheses, you have the calculation 16 \div 4 \times 5. Since it is the operations of multiplication and division, work from left to right.
Completing the division, you have 16 \div 4=4.
Next, 4 \times 5=20.
Therefore, 16 \div 4 \times 5=20.
Replacing 16 \div 4 \times 5 with 20, you now have the updated calculation: 12+20^2.
Solve for any exponents.
Now solve 20^2=20 \times 20=400.
Updating the calculation, you now have 12+400.
Solve any division and multiplication calculations.
There is no division or multiplication left to solve.
Solve any addition and subtraction calculations.
12+400=412 which gives us the final answer:
12+(16 \div 4 \times 5)^2=412
Teaching tips for properties of equality
- The properties are not useful in all solving situations. Be intentional about choosing practice problems that lend themselves to being solved with the associative, commutative, and distributive properties.
- Incorporate models (array or area) into instruction when working with the distributive property, especially in the beginning. This will help students build a conceptual understanding and make it easier for them to adapt their thinking to variables when the time comes.
- Instead of just giving students the definitions of each property, draw attention to examples of them as they come up in daily math activities. You may even create and update an anchor chart each time a student notices one of the properties naturally. Over time, students will start recognizing them on their own. Once this happens, you can introduce the property name and mathematical definition by using the student examples.
- Include plenty of student discourse around the properties so that students understand that using the properties creates equivalent equations, even though they are written differently. This could include students sharing their thinking and analyzing the thinking of their classmates.
- Find ways for students to practice the order of operations besides just using worksheets. For example, you can physically separate the answer choices and the word problems in the classroom. Students will be required to walk around to solve the problem and then find the answer that matches.
Easy mistakes to make
- Thinking there is only one way to use each property to solve
Often there is more than one way to use the associative, commutative, or distributive property when solving.
For example,
\begin{aligned} & 3 \times 5 \hspace{4cm} 3 \times 5\\ & =(1+2) \times 5 \hspace{2.8cm} =3 \times(4+1) \\ & =(1 \times 5)+(2 \times 5) \hspace{0.7cm} OR \hspace{0.8cm} =(3 \times 4)+(3 \times 1)\\ & =5+10 \hspace{3.4cm} =12+3 \\ & =15 \hspace{3.95cm} =15 \end{aligned}
- Using the associative property or commutative property for subtraction or division
The associative and commutative properties only work when changing the grouping or the order of the numbers doesn’t affect the answer. This does not work for subtraction or division.
For example,
or
\begin{aligned} & 10-(5-2) \ & =10-3 \ & =7 \end{aligned}or
\begin{aligned} & 5-10-2 \ & =-5-2 \ & =-7 \end{aligned}- Not decomposing by place value
When using the distributive property, break apart a number being multiplied so that the overall value stays the same. Otherwise, the products will not be equivalent. This includes correctly using the place value of the number.
For example,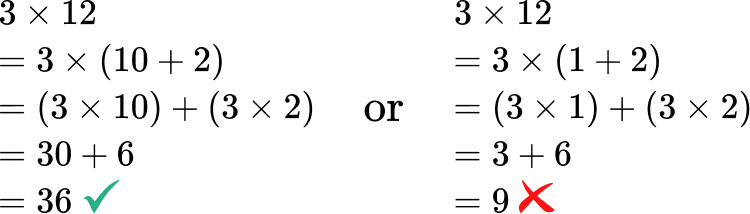
- Not following the order of operations correctly
Equations are always solved by moving from left to right and follow the sequence of PEMDAS. This also means that multiplication and division are done in order from left to right and addition and subtraction are done in order from left to right. Not following this order can lead to the wrong answer.
For example,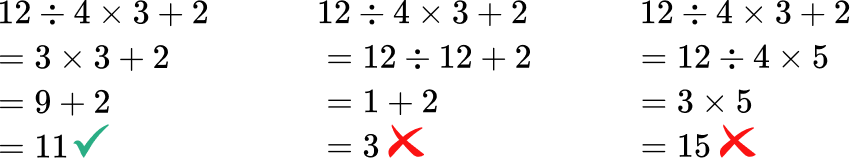
Practice properties of equality questions
1. Which of the following equations shows how to solve 4 \times 4 \times 10 using the associative property?
All the numbers are being multiplied, so the associative property can be used.
Change the grouping of the numbers and solve.
\begin{aligned} & 4 \times 4 \times 10 \\ & =4 \times(4 \times 10) \quad \text{ *Group and multiply these numbers first}\\ & =4 \times 40 \\ & =160 \end{aligned}
2. Which of the following equations shows how to solve 53 + 12 + 17 using the commutative property?
The commutative property says that changing the order in the equation does not change the sum.
\begin{aligned} & 53+12+17 \\ & =53+17+12 \;\; \text{ Change the order of 12 and 17} \\ & =70+12 \quad \quad \text{ *Adding 53 and 17 first gives us 70 – a friendly number} \end{aligned}
3. Which of the following equations shows how to solve 6 \times 3 \times 5 using the commutative property to create a friendly number?
The commutative property says that changing the order in the equation does not change the product.
Friendly numbers are numbers that are easy to multiply mentally – like multiples of 10.
\begin{aligned} & 6 \times 3 \times 5\\ & =6 \times 5 \times 3 \quad \text{ *Change the order of 3 and 5} \\ & =30 \times 3 \quad \quad \text{ *Multiplying 6 and 5 first gives us 30 – a friendly number} \end{aligned}
4. Which of the following equations shows 6 \times 7 using the distributive property?
The numbers are being multiplied, so the distributive property can be used.
\begin{aligned} & 6 \times 7 \\ & =6 \times(1+3+3) \quad \quad \quad \quad \quad \text{ *Break 7 up into } 1 + 3 + 3 \\ & =(6 \times 1)+(6 \times 3)+(6 \times 3) \;\; \text{ *Multiply 1, 3, and 3 by 6 } \\ & =6+18+18 \quad \quad \quad \quad \quad \quad \text{ *Add the partial products back together}\\ & =42 \end{aligned}
5. Calculate 7+3 \times 12.
To solve, follow the order of operations by using PEMDAS.
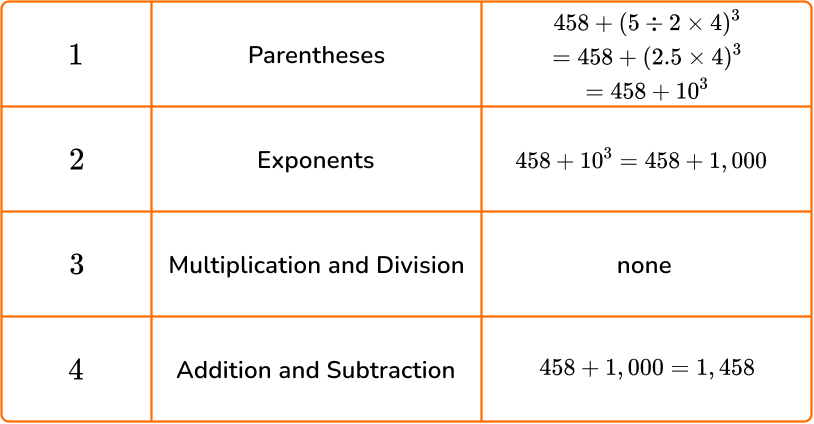
6. Calculate 458+(5 \div 2 \times 4)^3.
To solve, follow the order of operations by using PEMDAS.
Properties of equality FAQs
Yes, these properties can be applied to any equation, expression or inequality that includes real numbers (which includes fractions, decimals, negative and irrational numbers).
As students are learning the operations, they learn that subtraction is the inverse of addition and division is the inverse of multiplication.
As students work with the operations, they will begin to notice other patterns that are later formalized. These include the addition property of equality, subtraction property of equality, multiplication property of equality, and the division property of equality, where students learn that the same operation can be done to both sides of an equation without jeopardizing equality.
This is because the equal sign can be thought of as a balance, so as long as the same operation is done to both sides of the equation, equivalence is maintained.
As students begin to work with equations with unknown variables, they will learn that these are also algebraic properties that can be used when working with algebraic equations.
For example, students can use the distributive property to simplify linear equations and then use the addition property of equality and the division property of equality to solve for a specific value.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.
Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!