Percent Decrease - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Simplifying fractions Percent to decimal Percent to fraction

Math resources Ratio and proportion Percent

Percent decrease

Here you will learn about percent decrease, including how to decrease a value by a given percent, use multipliers to calculate percent decrease, and work out percent change.

Students will first learn about percent decrease as part of ratios and proportions in the 7th grade.

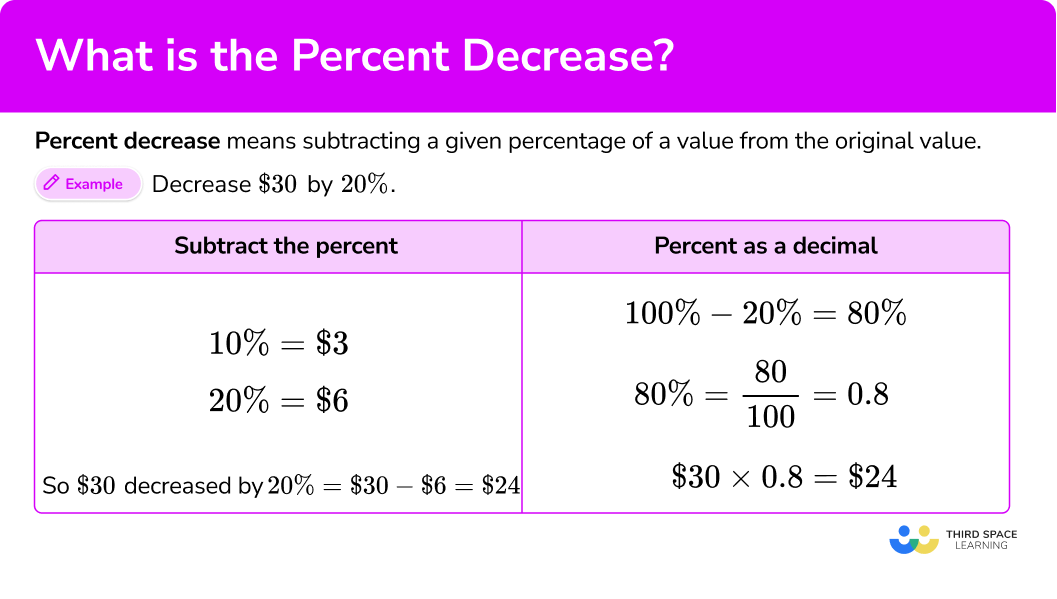
What is percent decrease?

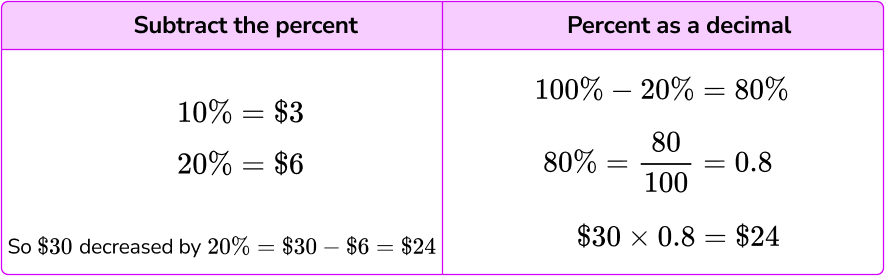
Percent decrease means subtracting a given percentage of a value from the original value. To do this, you can either calculate the given percent of the value and subtract it from the original or use a percent as a decimal.

For example,

Decrease $\$30$ by $20\%.$

When given two values, you can calculate the percent difference or percentage change. When the value goes down this may also be called percent decrease, percent loss, or a markdown.

You can calculate percent change using the percentage change formula:

$\text { Percent change }=\frac{\text { amount of change }}{\text { original }} \times 100$

Percent loss

Percent loss is when the percent decreases or gets smaller between a starting percent and the final percent.

For example,

At the beginning of the month, you had $\$150$ in your savings account, and by the end of the month, you had $\$75.$ Work out the percent decrease.

$\text { Percent decrease }=\cfrac{150-75}{150} \times 100=50 \%$

Markdowns

Markdowns are the decreased price of a good. Markdowns are more commonly known as discounts, or sales, in a retail store.

For example, at the end of the summer, stores will place their summer clothing and swimsuits on markdown to make room for their fall and winter clothing.

What is percent decrease?

Common Core State Standards

How does this relate to 7th grade math?

Grade 7: Ratios and Proportional Relationships (7.RP.3)
Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.

How to decrease a value by a percent

In order to decrease a value by a percent:

Calculate the given percent of the value.
Subtract the calculated percent from the original number.

[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of percents. 10+ questions with answers covering a range of 6th and 7th grade percent topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)

DOWNLOAD FREE

Percent decrease examples

Example 1: percent decrease

Decrease $\$80$ by $30\%.$

Calculate the given percent of the value.

You will need to calculate $30\%$ of $\$80.$

The easiest way to calculate $30\%$ is to calculate $10\%$ (by dividing by $10$ ) and then multiply by $3$ to get $30\%.$

$10\%$ of $\$80 = \$8$

$8 \times 3=24$

$30\%$ of $\$80 = \$24$

2Subtract the calculated percent from the original number.

You will subtract $\$24$ from the initial value of $\$80.$

$\$80-\$24 = \$56$

A $30\%$ decrease of $\$80$ is $\$56.$

Example 2: percent decrease

Decrease $250 \, km$ by $45\%.$

Calculate the given percent of the value.

You will calculate $45\%$ of $250$ by first finding $40\%.$

$10\%$ of $250 \, km = 25 \, km$

$25 \times 4=100$

$40\%$ of $250 \, km = 100 \, km$

You will then need to calculate $5\%.$ Find $10\%$ then divide by $2$ to find $5\%.$

$10\%$ of $250 \, km = 25 \, km$

$25 \div 2=12.5$

$5\%$ of $250 \, km = 12.5 \, km$

$100 \mathrm{~km}+12.5 \mathrm{~km}=112.5 \mathrm{~km}$

$45\%$ of $250 \, km = 112.5 \, km$

Subtract the calculated percent from the original number.

You will subtract $112.5 \, km$ from the original value.

$250-112.5 = 137.5 \, km$

A $45\%$ decrease of $250 \, km$ is $137.5 \, km.$

Example 3: percent decrease

Decrease $760$ by $40\%.$

Calculate the given percent of the value.

You will calculate $40\%$ of $760.$

$10\%$ of $760 = 76$

$76 \times 4=304$

$40\%$ of $760 = 304$

Subtract the calculated percent from the original number.

You will subtract $304$ from the original number.

$760-304=456$

A $40\%$ decrease of $760$ is $456.$

Example 4: a markdown

A jacket that costs $\$35.00$ is reduced by $15\%$ in a sale. Calculate the new price of the jacket.

Calculate the given percent of the value.

You will calculate $15\%$ of $\$35.$

You will calculate $15\%$ of $\$35$ by first finding $10\%.$

$10\%$ of $\$35 = \$3.50$

You will then need to calculate $5\%.$ Use $10\%$ then divide by $2$ to find $5\%.$

$10\%$ of $\$35 = \$3.50$

$3.50 \div 2=1.75$

$5\%$ of $\$35 = \$1.75$

$\$ 3.50+1.75=\$ 5.25$

$15\%$ of $\$35$ is $\$5.25.$

Subtract the calculated percent from the original number.

You will subtract $\$5.25$ from the original price.

$\$ 35.00-\$ 5.25=\$ 29.75$

The new price for the jacket is $\$29.75.$

Percent decrease using a percent as a decimal

In order to decrease a value by using a percent as a decimal:

Subtract the percent you are decreasing from $\bf{100\%}$ .
Convert the percent to a decimal.
Multiply the original amount by the decimal.

Example 5: percent as a decimal

Decrease $84 \, m$ by $46\%.$

Subtract the percent you are decreasing from $\bf{100\%}$ .

Here you are calculating a $46$ percent decrease so subtract $46\%$ from $100\%.$

$100 \%-46 \%=54 \%$

Convert the percent to a decimal.

To convert a percent to a decimal, you divide the percentage by $100.$

$54 \div 100=0.54$

$54\% = 0.54$

Multiply the original amount by the decimal.

You will multiply the starting value by the decimal.

$84\times 0.54=45.36 \, m$

$84 \, m$ decreased by $54\%$ is $45.36 \, m.$

Example 6: percent as a decimal

Daniel has $\$3,600.$ He spends $25\%$ of his money. How much does he have left?

Subtract the percent you are decreasing from $\bf{100\%}$ .

This is a $25$ percent decrease so subtract $25\%$ from $100\%.$

$100\%-25\% = 75\%$

Convert the percentage to a decimal.

To convert a percent to a decimal, you divide the percent by $100.$

$75 \div 100=0.75$

$75\% = 0.75$

Multiply the original amount by the decimal.

You will multiply $\$3,600$ by $0.75.$

$3,600 \times 0.75=\$ 2,700$

Daniel has $\$2,700$ left.

Calculating percent decrease

In order to calculate the percent decrease after a percent change:

Find the amount of change by subtracting the original number from the new number.
Plug numbers into the percent change formula.
$\text { Percentage change }=\cfrac{\text { Change }}{\text { Original }} \times 100$
Simplify the fraction, if necessary, using equivalent fractions.
Convert the fraction to a decimal.
Calculate percent change.

Example 7: calculating percent change

Ricky weighed $70 \, kg$ in March. By June his weight had decreased to $62 \, kg.$ Calculate the percent decrease in his weight.

Find the amount of change by subtracting the original number from the new number.

Ricky’s weight has changed from $70 \, kg$ to $62 \, kg.$ You will subtract his original weight from his new weight.

$70 \, kg-62 \, kg = 8 \, kg$

Plug numbers into the percent change formula.

The change is $8 \, kg$ and the original amount is $70 \, kg.$

$\begin{aligned} &\text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100\\\\ &\text { Percentage change }=\cfrac{8}{70} \times 100 \end{aligned}$

Simplify the fraction, if necessary, using equivalent fractions.

$\cfrac{8}{70} \,$ can be simplified to $\, \cfrac{4}{35} \, .$

$\text { Percent change }=\cfrac{4}{35} \times 100$

Convert the fraction to a decimal.

$\cfrac{4}{35}=0.114$

You can round this decimal to $0.11$ to solve.

$\text { Percent change }=0.11 \times 100$

Calculate percent change.

$0.11\times 100=11$

$\text{Percent change } = 11\%$

The percent decrease is about $11\%.$

Example 8: calculating percent loss

Louise buys a car for $\$7,500$ and sells it for $\$6,150$ two years later. Calculate Louise’s percent loss.

Find the amount of change by subtracting the original number from the new number.

The value has changed from $\$7,500$ to $\$6,150.$

$\$7,500-\$6,150 = \$1,350$

Plug numbers into the percent change formula.

The change is $\$1,350$ and the original amount is $\$7,500.$

$\text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100$

$\text { Percent change }=\cfrac{1350}{7500} \times 100$

Simplify the fraction, if necessary, using equivalent fractions.

$\cfrac{1,350}{7,500} \,$ can be simplified to $\, \cfrac{18}{100} \, .$

$\text { Percent change }=\cfrac{18}{100} \times 100$

Convert the fraction to a decimal.

$\cfrac{18}{100}=0.18$

$\text { Percent change }=0.18 \times 100$

Calculate percent change.

$0.18 \times 100=18$

$\text{Percent change }=18 \%$

Louise’s percent loss is $18\%.$

Teaching tips for percent decrease

There are times when the figures used to calculate percent change can be rather big. To help them with these tasks, students can use calculators or percentage change calculators.

Microsoft Excel may be used to calculate percent change. This could serve as an additional teaching point when talking about percent change with students who are comfortable with Excel.

Easy mistakes to make

Incorrectly converting percents to decimals
The most common mistakes are with single digit percents $(6\%),$ multiples of $10 \, (60\%)$ and decimal percentages $(1.2\%).$
Remember to divide the percent by $100$ to find the decimal.
For example, $6\%=0.06, \, 50\%=0.5, \, 1.2\%=0.012, \, 206.5\%=2.065$

Using an incorrect value for the denominator in the percentage decrease formula
Using the new value instead of the original value for the denominator when calculating percentage change.

Percent
Percent of a number
Simple interest
Percent change
Percent increase
Percent increase and decrease
Percent error
Exponential decay (coming soon)
Compound interest formula (coming soon)

Practice percent decrease questions

Calculate the percent decrease that has occurred in each of these questions.

7,480 \, m

7,520 \, m

9,000 \, m

6,000 \, m

First, you will need to calculate $20\%$ of $7,500.$

$10\%$ of $7,500 \, m = 750 \, m$

$750 \times 2=1,500$

$20\%$ of $7,500 \, m = 1,500 \, m$

Then you will subtract $1,500 \, m$ from the original value.

$7,500-1,500=6,000 \mathrm{~m}$

A $20\%$ decrease of $7,500 \, m$ is $6,000 \, m.$

9 \, ml

80 \, ml

36 \, ml

51 \, ml

First, you will need to calculate $80\%$ of $45 \, ml.$

$10\%$ of $45 \, ml = 4.5 \, ml$

$4.5 \times 8=36$

$80\%$ of $45 \, ml = 36 \, ml$

Then you will subtract $36 \, ml$ from the original value.

$45-36=9 \, ml$

An $80\%$ decrease of $45 \, ml$ is $9 \, ml.$

\$562.50

\$731

\$173

\$927.42

This is a $25$ percent decrease so start by subtracting $25\%$ from $100 \%.$

$100 \%-25 \%=75 \%$

Next, to convert a percent to a decimal, you divide the percent by $100.$

$75 \div 100=0.75$

$75\% = 0.75$

Then, you will multiply the original number, $\$750,$ by the decimal.

$750 \times 0.75=\$ 562.50$

$\$750$ decreased by $25\%$ is $562.50.$

215.8 \, g

6.65 \, g

97.028 \, g

150 \, g

This is a $40 percent decrease so start by subtracting 40\%$ from $100\%.$

$100 \%-40 \%=60 \%$

Next, to convert a percent to a decimal, you divide the percent by $100.$

$60 \div 100=0.60$

$60\% = 0.60$

Then, you will multiply the original number, $250 \, g,$ by the decimal.

$250 \times 0.60=150$

$250 \, g$ decreased by $40\%$ is $150 \, g.$

330\%

50.77 \%

49.23\%

203.125\%

Start by finding the amount of change by subtracting the original number from the new number.

The value has changed from $650 \, kg$ to $320 \, kg.$

$650-320=330 \, kg$

Next, plug numbers into the percent change formula.

The change is $330 \, kg$ and the original amount is $650 \, kg.$

$\text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100$

$\text { Percent change }=\cfrac{330}{650} \times 100$

If the fraction can be simplified, do that next.

$\cfrac{330}{650} \,$ can be simplified to $\, \cfrac{33}{65} \, .$

$\text {Percent change }=\cfrac{33}{65} \times 100$

Then you will convert the fraction to a decimal.

$\cfrac{33}{65}=0.51$

$\text {Percent change }=0.51 \times 100$

Then you will calculate the percent change.

$0.51 \times 100=51$

$\text {Percent change }=51 \%$

The percent change is a $51\%$ decrease.

18.25\%

85 \%

17.4\%

82.25\%

Start by finding the amount of change by subtracting the original number from the new number.

The value has changed from $\$11,500$ to $\$9,500.$

$11,500-9,500=\$ 2,000$

Next, plug numbers into the percent change formula.

The change is $\$2,000$ and the original amount is $\$11,500.$

$\text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100$

$\text { Percent change }=\cfrac{2,000}{11,500} \times 100$

If the fraction can be simplified, do that next.

$\cfrac{2,000}{11,500} \,$ can be simplified to $\, \cfrac{4}{23} \, .$

$\text {Percent change }=\cfrac{4}{23} \times 100$

Then you will convert the fraction to a decimal.

$\cfrac{4}{23}=0.174$

$\text {Percent change }=0.174 \times 100$

Then you will calculate the percent change.

$0.174 \times 100=17.4$

$\text {Percent change }=17.4 \%$

The tractor decreased in value by $17\%.$

Percent decrease FAQs

Can finding the percent change give you a negative number for a percent?

If you are finding a percent decrease, or any percentage where the value is decreasing, the initial percent change calculation will result in a negative number. However, you will use the absolute value of the difference to calculate the overall percent change, which will result in a positive number.

Is there a different formula to calculate percent increase and percent decrease?

You use the same formula whether you are finding the percent increase or decrease. With both, you are calculating the percent to which the measure either increases or decreases.

The next lessons are

Compound measures
Exponents
Converting fractions, decimals, and percentages
Algebraic expressions

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.