Add the percent you are increasing by and [katex] textbf{100%} [/katex].

[katex] 100 \%+20 \%=120 \% [/katex]

Subtract the percent you are decreasing from [katex] textbf{100%} [/katex].

This is a [katex] 15 \% [/katex] decrease, so you will subtract [katex] 15 \% [/katex] from [katex] 100 \%. [/katex] [katex] 100 \%-15 \%=85 \% [/katex]

Percent Increase And Decrease - Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Simplifying fractions Percent to decimal Percent to fraction

Math resources Ratio and proportion Percent

Percent increase and decrease

Here you will learn about percent increase and decrease, including how to increase and decrease a value by a given percentage, use decimals to calculate percent increase and percent decrease and find percent change.

Students will first learn about percent increase and decrease as part of ratios and proportions in the $7$ th grade.

What is the percent increase and decrease?

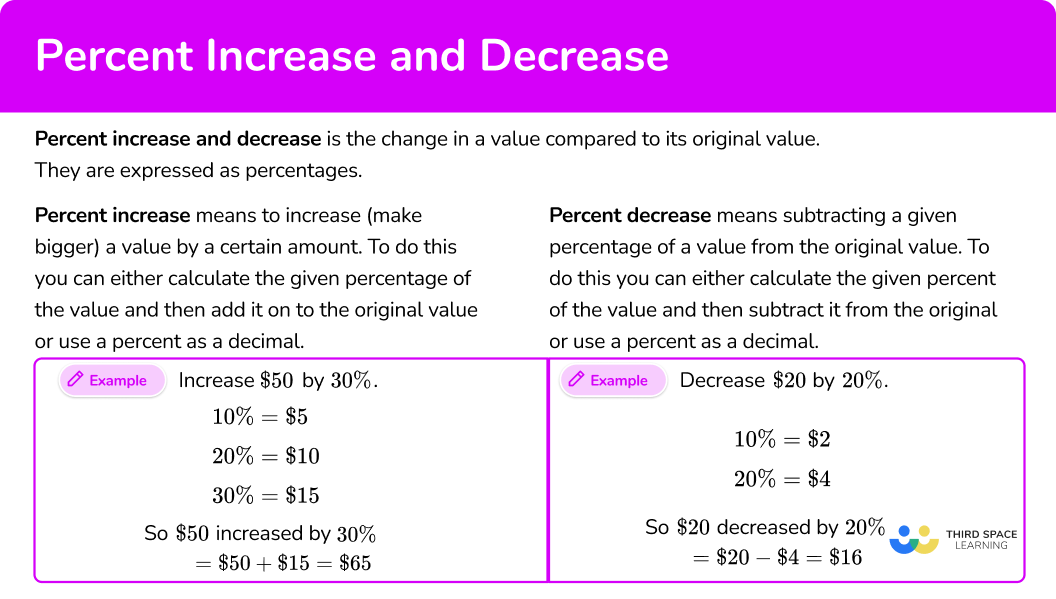
Percent increase and decrease is the change in a value compared to its original value. They are expressed as percentages.

Percent increase means to increase (make bigger) a value by a certain amount.

Percent decrease means to decrease (make smaller) a value by a certain amount.

In math, you may need to increase or decrease a value by a percentage or calculate a percentage change of two values.

To do increase a value by a percentage, you can either calculate the given percentage of the value and then add it on to the original value or use a percent as a decimal.

For example,

Increase $\$ 50$ by $30 \%.$

Add on the percent	Percent as a decimal
$\begin{aligned} & 10 \%=\$ 5 \\\\ & 20 \%=\$ 15 \\\\ & 30 \% = \$ 15 \end{aligned}$ So $\$50$ increased by $30\% = \$ 50+\$ 15=\$ 65.$	$\begin{aligned} & 100 \%+30 \%=130 \% \\\\ & 130 \%=\frac{130}{100}=1.3 \\\\ & \$ 50 \times 1.3=\$ 65 \end{aligned}$

To do decrease a value by a percentage, you can either calculate the given percent of the value and then subtract it from the original or use a percent as a decimal.

For example,

Decrease $\$ 20$ by $20 \%.$

Subtract the percent	Percent as a decimal
$\begin{aligned} & 10 \%=\$ 2 \\\\ & 20 \%=\$ 4 \end{aligned}$ So $\$20$ decreased by $20\% = \$ 20-\$ 4=\$ 16.$	$\begin{aligned} & 100 \%-20 \%=80 \% \\\\ & 80 \%=\frac{80}{100}=0.8 \\\\ & \$ 20 \times 0.8=\$ 16 \end{aligned}$

To calculate the percent difference or percentage change of two values, You can calculate percent change using the percentage change formula.

$\text { Percent change }=\frac{\text { amount of change }}{\text { original }} \times 100$

When the value goes down this may also be called percent decrease, percent loss, or a markdown.

What is the percent increase and decrease?

[FREE] Percent Increase And Decrease Worksheet (Grade 7)

Use this worksheet to check your 7th grade students’ understanding of percent increase and decrease. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Percent Increase And Decrease Worksheet (Grade 7)

Use this worksheet to check your 7th grade students’ understanding of percent increase and decrease. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7: Ratios and Proportional Relationships (7.RP.3)
Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.

How to increase or decrease a value by a percent

In order to increase or decrease a value by a given percent:

Calculate the given percent of the value.
Add or subtract the calculated percent to/from the original number.

Percent increase and decrease examples

Example 1: increase value by a percent

Increase $500$ by $50 \%.$

Calculate the given percent of the value.

You will first calculate $50 \%$ of $500.$

You can calculate $10 \%$ (by dividing by $10$ ) and then multiply by $5$ to get to $50 \%.$

$10 \%$ of $500=50$

$50 \times 5=250$

$50 \%$ of $500$ is $250.$

Note: You can also calculate $50 \%$ of an amount by dividing it by $2$ .

2Add or subtract the calculated percent to/from the original number.

Because you are calculating a percent increase, add $250$ on to the original value of $500.$

$500+250=750$

The final answer is $750.$

$500$ increased by $50 \%$ is $750.$

Example 2: decrease value by a percent

Decrease $\$ 1,200$ by $25 \%.$

Calculate the given percent of the value.

First, you will calculate $25 \%$ of $\$ 1,200.$

You can calculate $25 \%$ by first finding $10 \%$ (dividing by $10$ ), then multiplying by $2$ to find $20 \%.$

$10 \%$ of $\$ 1,200$ is $120.$

$20 \%$ of $\$ 1,200$ is $240.$

You can then find $5 \%,$ by dividing $120$ by $2.$

$120 \div 2=60.$

$5 \%$ of $\$ 1,200$ is $60.$

$240+60=300.$

$25 \%$ of $\$ 1,200$ is $300.$

Note: You can also calculate $25 \%$ of an amount by dividing it by $4$ .

Add or subtract the calculated percent to/from the original number.

Because you are calculating a percent decrease, you will subtract $\$ 300$ from the original value, $\$ 1,200.$

$1,200-300=900$

The final answer is $\$ 900.$

A $25 \%$ decrease of $\$ 1,200$ is $\$ 900.$

Percent increase and decrease using a percent as a decimal

In order to increase a value by using a percent as a decimal:

Add the percent you are increasing by and $\textbf{100\%}$ .
Convert the percent to a decimal.
Multiply the original amount by the decimal.

In order to decrease a value by using a percent as a decimal:

Subtract the percent you are decreasing from $\textbf{100\%}$ .
Convert the percent to a decimal.
Multiply the original amount by the decimal.

Example 3: percent increase using a percent as decimal

Increase $2,200 \, ml$ by $20 \%.$

Add the percent you are increasing by and $\textbf{100\%}$ .

$100 \%+20 \%=120 \%$

Convert the percent to a decimal.

Divide the percentage by $100.$

$120 \% \div 100=1.2$

$120 \%=1.2$

Multiply the original amount by the decimal.

Multiply $2,200$ by $1.2.$

$2,200 \times 1.2=2,640 \mathrm{~ml}$

$2,200 \, ml$ increased by $20 \%$ is $2,640 \, ml.$

Example 4: percent decrease using a percent as decimal

Kendra had a car payment of $\$ 430.$ When she purchased a new car, her car payment decreased $15 \%.$ How much is Kendra’s car payment now?

Subtract the percent you are decreasing from $\textbf{100\%}$ .

This is a $15 \%$ decrease, so you will subtract $15 \%$ from $100 \%.$

$100 \%-15 \%=85 \%$

Convert the percent to a decimal.

Now divide the percentage by $100.$

$\begin{aligned}&85 \div 100=0.85\\\\ &85 \%=0.85\end{aligned}$

Multiply the original amount by the decimal.

Multiply the original price of $\$ 430$ by $0.85.$

$430 \times 0.85=\$ 365.50$

Remember to always write money using two decimal places.

Kendra’s car payment decreased from $\$ 430$ to $\$ 365.50.$

Calculating percent increase and decrease

In order to calculate the percent increase or percent decrease after a percent change:

Find the amount of change using subtraction.
Plug numbers into the percent change formula.
$\text { Percentage change }=\cfrac{\text { Change }}{\text { Original }} \times 100$
Simplify the fraction, if necessary, using equivalent fractions.
Convert the fraction to a decimal.
Calculate percent change.

Example 5: percent decrease after a percent change

Karla weighed $67 \, kg$ in January. Over a period of time, her weight had decreased to $55 \, kg.$ Calculate the percent decrease in her weight.

Find the amount of change using subtraction.

Karla’s weight has changed from $67 \, kg$ to $55 \, kg.$ You will subtract her original new from her original weight.

$67 \mathrm{~kg}-55 \mathrm{~kg}=12 \mathrm{~kg}$

Plug numbers into the percent change formula.

The change is $12 \, kg$ and the original amount is $67 \, kg.$ Plug the numbers into the following formula:

$\begin{aligned}& \text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100 \\\\ &\text { Percent change }=\cfrac{12}{67} \times 100\end{aligned}$

Simplify the fraction, if necessary, using equivalent fractions.

$\cfrac{12}{67} \,$ is already in simplest form.

Convert the fraction to a decimal.

$\cfrac{12}{67}=0.1791$

You can round this decimal number to $0.18$ to solve.

$\text { Percent change }=0.18 \times 100$

Calculate percent change.

$0.18\times 100=18$

$\text { Percent change }=18 \%$

The percent decrease is about $18 \%.$

Example 6: percent increase after a percent change

The cost of a cup of coffee has increased from $\$ 2.75$ to $\$ 3.50.$ Find the percent increase in cost of a cup of coffee.

Find the amount of change using subtraction.

The cost of a cup of coffee has changed from $\$ 2.75$ to $\$ 3.50.$ You will subtract the old cost from the new cost.

$\$ 3.50-\$ 2.75=\$ 0.75$

Plug numbers into the percent change formula.

Apply the percent change formula. The amount of increase is $\$ 0.75$ and the original price is $\$ 2.75.$ Plug the numbers into the following formula:

$\begin{aligned}& \text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100 \\\\ & \text { Percent change }=\cfrac{0.75}{2.75} \times 100\end{aligned}$

Simplify the fraction, if necessary, using equivalent fractions.

$\cfrac{0.75}{2.75}$ can be simplified to $\cfrac{3}{11}.$

$\text{ Percent change }=\cfrac{3}{11} \times 100$

Convert the fraction to a decimal.

$\cfrac{3}{11}=0.2727...$

You can round this decimal number to $0.27$ to solve.

$\text { Percent change }=0.27 \times 100$

Calculate percent change.

$0.27\times 100=27$

$\text { Percent change }=27 \%$

The percent increase is about $27 \%.$

[FREE] Percents Worksheet (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of percents. 10+ questions with answers covering a range of 6th and 7th grade percent topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Percents Worksheet (Grade 6 to 7)

DOWNLOAD FREE

Teaching tips for percent increase and decrease

Microsoft Excel provides a way to calculate percent change. Students who possess Excel proficiency can further enhance their understanding of percent change by exploring this additional teaching aspect.

There are times when the figures used to calculate percent change can be large. To help them with calculating, students can use calculators or percentage change calculators.

Easy mistakes to make

Believing that percents cannot exceed $\textbf{100\%}$
Percent increase or decrease can be greater than $100 \%.$ It simply means that the value has more than doubled (in case of an increase) or more than halved (in case of a decrease).

Incorrectly converting percentages to decimals
The most common mistakes are with single digit percentages (for example, $7 \%$ ), multiples of $10$ (for example, $50 \%$ ) and decimal percentages (for example $4.5 \%$ ). Remember to divide the percentage by $100$ to find the decimal. For example,
$7 \%=0.07,\, 50 \%=0.5, \, 4.5 \%=0.045.$

Using an incorrect value for the denominator in the percentage increase formula
Use the new number instead of the original value for the denominator when calculating percent increase.

Percent increase and decrease practice questions

\$ 112.50

\$ 562.50

\$ 90.00

\$ 658.00

First, calculate $25 \%$ of $\$ 450.$

$\begin{aligned}& 10 \% \text { of } 450=45 \\\\ & 20 \% \text { of } 450=90 \\\\ & 25 \% \text { of } 450=112.5\end{aligned}$

Because you are calculating a percent increase, add $112.5$ on to the original value of $450.$

$450+112.5=562.5$

Remember when representing money, there should be two decimal places.

The final answer is $\$ 562.50.$

72 \, m

60 \, m

48 \, m

12 \, m

First, you will need to calculate $60 \%$ of $120 \, m.$

$10 \%$ of $120 \, m = 12 \, m$

$12 \times 6=72$

$60 \%$ of $120 \, m = 72 \, m$

Then you will subtract $72 \, m$ from the original value.

$120-72=48 \mathrm{m}$

A $60 \%$ decrease of $120 \, m$ is $48 \, m.$

121.00

52.03

43.32

56.47

Add the percentage you are increasing by, $21 \%,$ and $100.$

$100+21 =121$

Next, you will convert the percentage to a decimal by dividing.

$121 \div 100=1.21$

Then multiply the original amount by the decimal.

$43 \times 1.21=52.03$

$43$ increased by $21 \%$ is $52.03.$

\$ 491.50

\$ 240.00

\$ 560.00

\$ 506.00

This is a $30$ percent decrease so start by subtracting $30 \%$ from $100 \%.$

$100 \%-30 \%=70 \%$

Next, to convert a percent to a decimal, you divide the percent by $100.$

$70 \div 100=0.70$

$70 \% = 0.70$

Then, you will multiply the original number $, \$ 800,$ by the decimal.

$800 \times 0.70=\$ 560.00$

$\$ 800$ decreased by $30 \%$ is $\$ 560.00.$

87 \%

260 \%

300 \%

81 \%

First, you will calculate the change from $300 \, ml$ to $560 \, ml.$

$560-300=260$

The change is $260 \, ml,$ so you can now plug the numbers into the percent change formula.

$\text { Percent change }=\cfrac{260}{300} \times 100$

After simplifying the fraction to $\cfrac{13}{15},$ you would convert it to the decimal $0.87.$

$\begin{aligned}& 0.87 \times 100=87 \\\\ & \text { Percentage increase }=87 \%\end{aligned}$

150 \%

21 \%

32 \%

112 \%

Start by finding the amount of change by subtracting the original number from the new number.

The value has changed from $725 \, kg$ to $575 \, kg.$

$725-575=150 \mathrm{~kg}$

Next, plug numbers into the percent change formula. The change is $150 \, kg$ and the original amount is $725 \, kg.$

$\begin{aligned}& \text { Percent change }=\cfrac{\text { Change }}{\text { Original }} \times 100 \\\\ &\text { Percent change }=\cfrac{150}{725} \times 100\end{aligned}$

If the fraction can be simplified, do that next.

$\cfrac{150}{725}$ can be simplified to $\cfrac{6}{29}.$

$\text { Percent change }=\cfrac{6}{29} \times 100$

Then you will convert the fraction to a decimal.

$\begin{aligned}& \cfrac{6}{29}=0.21 \\\\ & \text { Percent change }=0.21 \times 100\end{aligned}$

Then you will calculate the percent change.

$0.21 \times 100=21$

$\text { Percent change }=21 \%$

The percent change is a $21 \%$ decrease.

Percent increase and decrease FAQs

Can percent increase or decrease be a negative number?

No, percent increase or decrease cannot be a negative value. The negative sign is used to indicate the direction of change (increase or decrease), but the percent itself is always a positive value.

How do I interpret a percent increase or decrease?

A positive percent increase indicates growth or expansion, while a percent decrease represents a reduction or contraction. For example, a $20 \%$ increase means the value has grown by $20 \%,$ whereas a $10 \%$ decrease means the value has decreased by $10 \%.$

The next lessons are

Compound measures
Converting fractions decimals and percentages
Ratio
Decimals

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.