[FREE] Fun Math Games & Activities Packs
Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!
In order to access this I need to be confident with:
Simplifying fractions Percent to decimal Percent to fractionPercent change
Here you will learn about percent change, including how to calculate the percentage by which a value has increased or decreased.
Students will first learn about percent change as part of ratios and proportional relationships in 7th grade.
What is percent change?
Percent change equals the change in value divided by the absolute value of the original value, multiplied by 100. It is when the percentage of its original value has changed to either increase or decrease the value.
When you calculate percent change, you are calculating by what percentage of its original value something has changed.
To calculate percent change, you can use the percentage change formula:
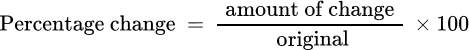
Percent change can refer to many different types of scenarios. This can include percentage increase, percentage decrease, percentage profit, percentage gain, markups and markdowns, or percentage loss.
Percent increase
Percentage increase, or percent gain, is when the percent increases, or gets bigger, between a starting percent and the final percent.
For example, at the beginning of the month you had \$50 in your savings account and by the end of the month you had \$75, you may want to find the percentage increase of the money you saved over the period of time.
Percent decrease
Percentage decrease, or percent loss, is when the percent decreases, or gets smaller, between a starting percent and the final percent.
For example, buying a tank of gas last year was cheaper than it is now. You could calculate the percent decrease in the amount of a gallon of gas.
Percent profit
Percentage profit refers to when a store or person is selling a good or a service, and they want to calculate the difference between the cost price and the selling price and represent it as a percent.
For example, a school store buys pencils for \$0.50 a piece, but sells them to the students for \$0.75. The school store would make \$0.25 profit, or 50\% profit.
Markups and markdowns
Markups are the increased price of a good, and markdowns are the decreased price of a good.
Markdowns are more commonly known as discounts or sales in a retail store.
A company may markup an item that is in high demand, and people are willing to pay more money for it.
What is the percent change?

Common Core State Standards
How does this relate to 7th grade math?
- Grade 7: Ratios and Proportional Relationships (7.RP.3)
Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
How to calculate percent change
In order to calculate percent change, you need to:
- Find the amount of change by subtracting the original number from the new number.
- Plug numbers into the percent change formula.
\text { Percentage change }=\cfrac{\text { Change }}{\text { Original }} \times 100 - Simplify the fraction, if necessary, using equivalent fractions.
- Convert the fraction to a decimal.
- Calculate percent change.
![[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Percents-check-for-understanding-quiz-listing-image-.png)
[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)
![[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Percents-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of percents. 10+ questions with answers covering a range of 6th and 7th grade percent topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Percents-check-for-understanding-quiz-listing-image-.png)
[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)
![[FREE] Percents Check for Understanding Quiz (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Percents-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of percents. 10+ questions with answers covering a range of 6th and 7th grade percent topics to identify areas of strength and support!
DOWNLOAD FREEPercent change examples
Example 1: percent increase
The weight of a baby has increased from 4 \, kg to 7 \, kg. Find the percentage difference in the baby’s weight.
- Find the amount of change by subtracting the original number from the new number.
The baby’s weight has increased from 4 \, kg to 7 \, kg. Calculate the percent change:
7-4=3 \mathrm{~kg}
2Plug numbers into the percent change formula.
The change is 3 \, kg and the original number is 4. Apply the percent change formula:
\begin{aligned} & \text {Percent change }=\cfrac{\text { change }}{\text { original }} \times 100 \\\\ & \text {Percent change }=\cfrac{3}{4} \times 100 \end{aligned}
3Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{3}{4} \, does not need to be simplified.
\text {Percent change }=\cfrac{3}{4} \times 100
4Convert the fraction to a decimal.
\cfrac{3}{4}=0.75
\text{Percent change } =0.75 \times 100
5Calculate percent change.
\begin{aligned} & 0.75 \times 100=75 \\\\ & \text {Percent change }=75 \% \end{aligned}
The final answer is 75\% percent change. The baby’s weight increased by 75\%.
Example 2: percent loss
Anna bought a computer for \$1,200. \; 2 years later, Anna sold the computer for \$800.
Calculate Anna’s percent loss.
Find the amount of change by subtracting the original number from the new number.
The initial price is \$1,200 and the new price is \$800. Calculate the change:
\$ 1,200-\$ 800=\$ 400
Plug numbers into the percent change formula.
The change is \$400 and the original price is \$1,200. Apply the percentage change formula:
\begin{aligned} & \text {Percent change }=\cfrac{\text { change }}{\text { original }} \times 100 \\\\ & \text {Percent change }=\cfrac{400}{1,200} \times 100 \end{aligned}
Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{400}{1,200} \, can be simplified to \, \cfrac{1}{3}.
\text {Percent change }=\cfrac{1}{3} \times 100
Convert the fraction to a decimal.
\cfrac{1}{3}=0.33…
This is a repeating decimal, but you can round to 0.33 to solve.
\text {Percent change }=0.33 \times 100
Calculate the percent change.
\begin{aligned} & 0.33 \times 100=33 \\\\ & \text {Percent change }=33 \% \end{aligned}
After selling the computer, Anna had a 33\% percent loss in the money she earned.
Example 3: percent profit
Matthew bought an antique for \$360. He sold it for \$396. Calculate Mattew’s percentage profit.
Find the amount of change by subtracting the original number from the new number.
The initial price is \$360 and the new price is \$396. Calculate the change:
\$396-\$360 =\$36
Plug numbers into the percent change formula.
\begin{aligned} \text {Percent change }&=\cfrac{\text { Change }}{\text { Original }} \times 100 \\\\ \text {Percent change }&=\cfrac{36}{360} \times 100 \end{aligned}
Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{36}{360} \, can be simplified to \, \cfrac{1}{10}.
\text {Percent change }=\cfrac{1}{10} \times 100
Convert the fraction to a decimal.
\cfrac{1}{10}=0.1
\text {Percent change }=0.1 \times 100
Calculate the percent change.
\begin{aligned} & 0.1 \times 100=10 \\\\ & \text {Percent change }=10 \% \end{aligned}
Matthew earned a 10\% profit when selling the antique.
Example 4: percent decrease
A clothing shop reduced the price of a jacket from \$48 to \$36. Find the percentage decrease.
Find the amount of change by subtracting the original number from the new number.
The starting value is \$48 and the new value is \$36. Calculate the change:
\$48-\$36 = \$12
Plug numbers into the percent change formula.
\begin{aligned} \text {Percent change }&=\cfrac{\text { Change }}{\text { Original }} \times 100 \\\\ \text {Percent change }&=\cfrac{12}{48} \times 100 \end{aligned}
Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{12}{48} \, can be simplified to \, \cfrac{1}{4}.
\text {Percent change }=\cfrac{1}{4} \times 100
Convert the fraction to a decimal.
\cfrac{1}{4}=0.25
\text {Percent change }=0.25 \times 100
Calculate the percent change.
\begin{aligned} & 0.25 \times 100=25 \\\\ & \text {Percent change }=25 \% \end{aligned}
The price of the jacket was decreased by 25\%.
More than one percent change
Sometimes, a product in a shop may be discounted twice, or the value of something may increase and then decrease. It is common to think that you can just add the percentage changes together, but this does not work.
For example, if something is reduced by 10\% in a sale and the sale price is then reduced by 10\%, this does not mean a total reduction of 20\%. This is because 10\% of the sale price is not the same as 10\% of the original price.
To calculate the total percent change after two percentage changes:
- Apply the first percent change.
- Apply the second percent change.
- Calculate the percent change between the final value and the original value and plug numbers into the percent change formula.
- Simplify the fraction, if necessary, using equivalent fractions.
- Convert the fraction to a decimal.
- Calculate the percent change.
Example 5: double percentage reduction
A television was priced at \$500 and was reduced by 10\% in a sale. 2 weeks later, the sale price was reduced by 10\%. Find the overall percentage reduction in price.
Apply the first percent change.
10\% of \$500 = \$50
\$500-\$50 = \$450
Apply the second percent change.
10\% of \$450 = \$45
\$450-\$45 = \$405
Calculate the percent change between the final value and the original value and plug numbers into the percent change formula.
The old value is \$500 and the new value is \$405.
Change: \$500-\$405 = \$95
\begin{aligned}
& \text {Percent change }=\cfrac{\text { change }}{\text { original }} \times 100 \\\\
& \text {Percent change }=\cfrac{95}{500} \times 100
\end{aligned}
Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{95}{500} \, can be simplified to \, \cfrac{19}{100}.
\text{Percent change }=\cfrac{19}{100} \times 100
Convert the fraction to a decimal.
\begin{aligned} &\cfrac{19}{100}=0.19 \\\\ &\text {Percent change }=0.19 \times 100 \end{aligned}
Calculate the percent change.
\begin{aligned} & 0.19 \times 100=19 \\\\ & \text {Percent change }=19 \% \end{aligned}
The television price has decreased by 19\% over the two weeks.
Example 6: percentage decrease and increase
Holly bought a diamond ring for \$2,000 in 2015. By 2017, the value of the ring had decreased by 5\%. By 2020, the value of the ring had increased by 20\% from its value in 2017.
Find the overall percentage change in the value of the diamond ring.
Apply the first percent change.
5\% of \$2,000 = \$100
\$2,000-\$100 = \$1,900
Apply the second percent change.
20\% of \$1,900 = \$380
\$1,900+\$380 = \$2,280
Calculate the percent change between the final value and the original value and plug numbers into the percent change formula.
Change: \$2,280-\$2,000 = \$280
\begin{aligned}
& \text {Percent change }=\cfrac{\text { change }}{\text { original }} \times 100 \\\\
& \text {Percent change }=\cfrac{280}{2,000} \times 100
\end{aligned}
Simplify the fraction, if necessary, using equivalent fractions.
\cfrac{280}{2,000} \, can be simplified to \, \cfrac{7}{50}.
\text{Percent change }=\cfrac{7}{50} \times 100
Convert the fraction to a decimal.
\begin{aligned} & \cfrac{7}{50}=0.14\\\\ & \text {Percent change }=0.14 \times 100 \end{aligned}
Calculate the percent change.
\begin{aligned} & 0.14 \times 100=14 \\\\ & \text {Percent change }=14 \% \end{aligned}
The value of Holly’s diamond ring increased by 14\% .
Teaching tips for percent change
- When calculating percent change, sometimes the numbers can be quite large. Students may use a calculator or a percentage change calculator to assist them with solving these problems.
- Percent change can be calculated using Microsoft Excel. For students who are proficient using Excel, this could be an additional teaching point while discussing percent change.
Easy mistakes to make
- Using an incorrect value for the denominator in the percent increase formula
Using the new value instead of the original value for the denominator when calculating percentage change will lead to an incorrect percent.
- Adding together multiple percent changes to find total percent change
Adding the percentages together to find the total percentage change does not work. Remember that a percentage of an already increased or decreased value will be different from a percentage of the original value.
Related lessons on percent
- Percent
- Percent of a number
- Percent decrease
- Simple interest
- Percent increase
- Percent increase and decrease
- Percent error
- Exponential decay
- Compound interest formula
Percent change practice questions
Calculate the percent change that has occurred in each of these questions.
1. \$400 increased to \$568.




First, you will calculate the change from \$400 to \$568.
568-400=168
The change is \$168, so you can now plug the numbers into the percent change formula.
\text{Percent change }=\cfrac{168}{400} \times 100
After simplifying the fraction to \, \cfrac{42}{100} \, , you would convert it to the decimal 0.42.
0.42 \times 100=42
\text{Percentage increase } =42 \%
2. 70 \, kg reduced to 59 \, kg.




First, you will calculate the change from 70 \, kg to 59 \, kg.
70-59=11
The change is 11, so you can now plug the numbers into the percent change formula.
\text{Percent change }=\cfrac{11}{70} \times 100
\cfrac{11}{70} \, is in simplest terms, you would convert it to the decimal 0.16, rounded to two decimal places.
0.16 \times 100=16
\text{Percentage reduced } =16 \%
3. 60 \, cm increased to 75 \, cm.




First, you will calculate the change from 60 \, cm to 75 \, cm.
75-60=15
The change is 15, so you can now plug the numbers into the percent change formula.
\text{Percent change }=\cfrac{15}{60} \times 100
After simplifying the fraction to \, \cfrac{1}{4} \, , you would convert it to the decimal 0.25.
0.25 \times 100=25
\text { Percentage increased }=25 \%
4. \$90 reduced to \$63.




First, you will calculate the change from \$90 to \$63.
90-63=27
The change is 27, so you can now plug the numbers into the percent change formula.
\text{Percent change }=\cfrac{27}{90} \times 100
After simplifying the fraction to \, \cfrac{3}{10} \, , you would convert it to the decimal 0.30.
0.30 \times 100=30
\text {Percentage reduced }=30 \%
5. \$500 increased by 20\% and then increased again by a further 10\%.




First, you will apply the first percent change, a 20\% increase to \$500.
20\% of \$500 = \$100
\$500 + \$100 = \$600
Next, apply the second percent change, a 10\% increase to \$600.
10\% of \$600 = \$60
\$600 + \$60 = \$660
The overall change is \$160, so you can now plug the numbers into the percent change formula.
\text {Percent change }=\cfrac{160}{500} \times 100
After simplifying the fraction to \, \cfrac{8}{25} \, , you would convert it to the decimal 0.32.
0.32 \times 100=32
\text {Percentage increased } = 32\%
6. \$6,000 increased by 20\% and then decreased by 25\%.
22.5\% decrease

22.5\% increase

10\% decrease

10\% increase

First, you will apply the first percent change, a 20\% increase from \$6,000.
20\% of \$6,000 = \$1,200
\$6,000 + \$1,200 = \$7,200
Next, apply the second percent change, a 25\% decrease from \$7,200.
25\% of \$7,200 = \$1,800
\$7,200-\$1,800 = \$5,400
The overall change is \$600, so you can now plug the numbers into the percent change formula.
\text {Percent change }=\cfrac{600}{6,000} \times 100
After simplifying the fraction to \, \cfrac{1}{10} \, , you would convert it to the decimal 0.10.
0.10 \times 100=10
\text {Percentage decreased } = 10\%
Percent change FAQs
If you are finding a percent decrease, or any percentage where the value is decreasing, the initial percent change calculation will result in a negative number. However, you will use the absolute value of the difference to calculate the overall percent change, which will result in a positive number.
You use the same formula whether you are finding the percentage increase or decrease. With both, you are calculating the percentage to which the measure either increases or decreases.
The next lessons are
- Compound measures
- Converting fractions, decimals, and percentages
- Exponents
- Simplifying fractions
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!