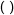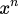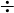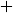High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Arithmetic Exponents Rational numbers Adding and subtracting rational numbersOrder of operations
Here you will learn about order of operations, including what it means and how to calculate and solve order of operations problems using PEMDAS.
Students will first learn about order of operations as a part of operations and algebraic thinking in elementary school.
What is the order of operations?
Order of operations refers to the rule that explains the sequence of steps necessary for correctly evaluating a mathematical expression or math problem.
You will use the acronym PEMDAS to help recall the correct order, or priority, in which you complete mathematical operations.
Mathematical operations such as multiplication and addition have to be completed in a specific order. This sequence of steps helps us to evaluate any mathematical expression, both with numerical values and algebraic expressions.
To evaluate an expression using PEMDAS, you need to understand what PEMDAS represents and be able to apply the PEMDAS rule to any calculation.
PEMDAS stands for:
Parentheses, Exponents, Multiplication and Division, Addition and Subtraction
Parentheses have a higher priority than exponents, so we calculate what is inside a pair of parentheses first. Exponents have a higher priority than division and multiplication, so any exponent that can be evaluated is calculated next, and so on.
The order can be remembered using the mnemonic device for PEMDAS, ‘Please Excuse My Dear Aunt Sally.’
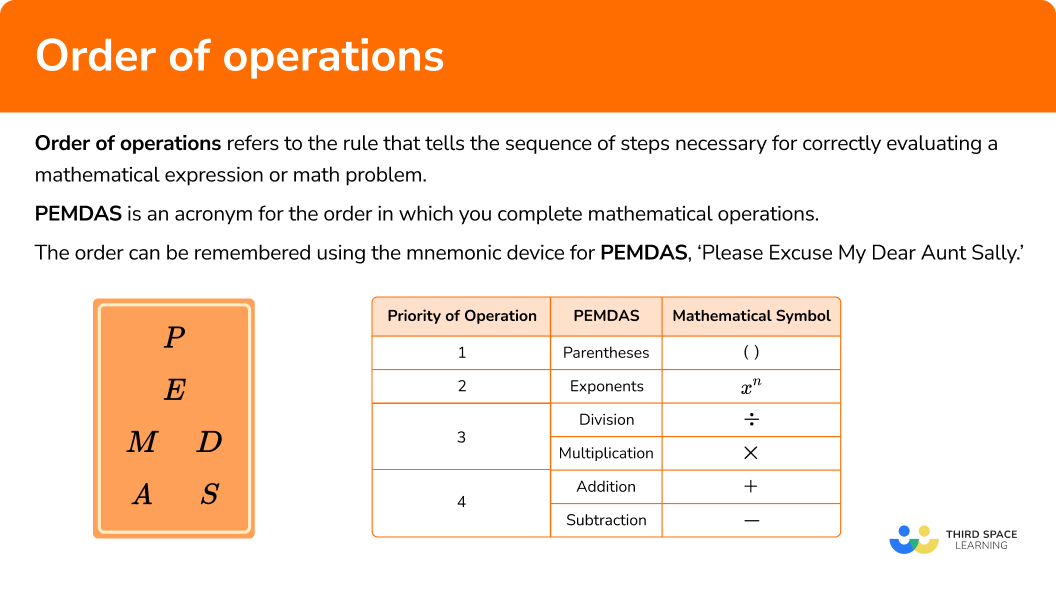
Order of operations
| Priority of Operation | PEMDAS | Mathematical Symbol |
|---|---|---|
| 1 | Parentheses | |
| 2 | Exponents | |
| 3 | Division
Multiplication | |
| 4 | Addition Subtraction | \bf{−} |
It is important to note that multiplication and division are given equal priority, and addition and subtraction are given equal priority.
When completing calculations that involve multiplication and division or addition and subtraction, you work from left to right.
For example,
Consider the following expression 12-7+6.
12-7=5 and then 5+6=11
For example,
Consider the following expression 10 \div 5 \times 2.
10 \div 5=2 and then calculate 2 \times 2=4.
Visually you could represent PEMDAS as:

What is the order of operations?
Common Core State Standards
How does this relate to 5th grade math and 6th grade math?
- Grade 5: Operations and Algebraic Thinking (5.OA.1)
Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.
- Grade 5: Operations and Algebraic Thinking (5.OA.2)
Write simple expressions that record calculations with numbers, and interpret numerical expressions without evaluating them.
- Grade 6: Expressions and Equations (6.EE.1)
Write and evaluate numerical expressions involving whole-number exponents.
How to evaluate using order of operations
In order to evaluate expressions using order of operations, you would use PEMDAS:
- Solve any calculations within parentheses.
- Solve for any exponents.
- Solve any division and multiplication calculations.
- Solve any addition and subtraction calculations.
![[FREE] Order Of Operations Worksheet (Grade 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Order-of-Operations-Worksheet-listing-image.png)
[FREE] Order Of Operations Worksheet (Grade 5 and 6)
![[FREE] Order Of Operations Worksheet (Grade 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Order-of-Operations-Worksheet-listing-image.png)
Use this worksheet to check your 5th and 6th grade students’ understanding of order of operations. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Order Of Operations Worksheet (Grade 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Order-of-Operations-Worksheet-listing-image.png)
[FREE] Order Of Operations Worksheet (Grade 5 and 6)
![[FREE] Order Of Operations Worksheet (Grade 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2025/01/Order-of-Operations-Worksheet-listing-image.png)
Use this worksheet to check your 5th and 6th grade students’ understanding of order of operations. 15 questions with answers to identify areas of strength and support!
DOWNLOAD FREEOrder of operations examples
Example 1: PEMDAS with addition and multiplication
Evaluate 3+6\times{7}.
- Solve any calculations within parentheses.
There are no parentheses.
2Solve for any exponents.
There are no exponents.
3Solve any division and multiplication calculations.
The multiplication that we need to calculate is 6\times{7}=42.
Replacing 6\times{7} with 42 gives us the calculation 3+42.
4Solve any addition and subtraction calculations.
3+42=45
So 3+6\times{7}=45
Example 2: PEMDAS with division and subtraction
Evaluate 12-8\div{2}.
There are no parentheses.
There are no exponents.
The division you need to calculate is 8\div{2}=4.
Replacing 8\div{2} with 4 gives us the calculation 12-4.
12-4=8
So 12-8\div{4}=8
Example 3: PEMDAS with parentheses and multiplication
Evaluate 3(2+4\times{6}-3).
You have a pair of parentheses and so you need to resolve what is inside the set of parentheses first. This is the calculation 2+4\times{6}-3.
Using PEMDAS, multiplication comes before addition and subtraction so you need to solve the multiplication 4\times{6}=24.
Replacing 4\times{6} with 24 in the calculation, you have 2+24-3.
Addition and subtraction should be completed from left to right and so you have 2+24=26 and 26-3=23. Therefore 2+24-3=23.
As 2+4\times{6}-3=23 and 3(2+4\times{6}-3) means 3\times(2+4\times{6}-3), you have the updated calculation 3\times{23}.
There are no exponents.
3\times{23}=69
There is nothing else to solve, so the final answer is:
3(2+4\times{6}-3)=69
Example 4: PEMDAS with an exponent and multiplication
Evaluate 4\times{3}^{2}.
There are no parentheses.
Here you have to resolve 3^{2}=3\times{3}=9.
Replacing 3^{2} with 9 in the calculation, you now have:
4\times{9}
The final step needed is to calculate 4\times{9}=36
There is nothing else to solve, so the final answer is:
4\times{3}^{2}=36
Example 5: PEMDAS with brackets, an exponent and division
Evaluate 3+(10\div{4}\times{20})^{2}.
Within the set of parentheses, you have the calculation 10\div{4}\times{20}.
You need to work from left to right.
Completing the division, you have 10\div{4}=2.5
Next, 2.5\times{20}=50
Therefore, 10\div{4}\times{20}=50.
Replacing 10\div{4}\times{20} with 50, you now have the updated calculation,
3+50^{2}
You now have to solve 50^{2}=50\times{50}=2500.
Updating the calculation, you now have 3+2500.
There are no divisions or multiplications to solve.
3+2500=2503 which gives us the final answer:
3+(10\div{4}\times{20})^{2}=2503
Example 6: PEMDAS with everything
Evaluate 4^{2}+2(14-8)\div{3}.
Within the brackets is the calculation 14-8=6.
Updating the calculation by changing the value in the bracket to 6, you have
4^{2}+2\times{6}\div{3}
As 4^2=4 \times 4=16, you now have
16+2\times{6}\div{3}
Here you have to calculate 2\times{6}\div{3}. Working from left to right, you calculate 2\times{6} and then divide the solution by 3.
2\times{6}=12
12\div{3}=4
Updating the calculation, you now have 16+4.
As 16+4=20, our final answer is:
4^{2}+2(14-8)\div{3}=20
Teaching tips for order of operations
- While PEMDAS is a great way for students to remember the order of operations, it’s important that the students understand how to solve for each of the operations required, not simply giving them the acronym to memorize.
- It is important to find a way for students to practice outside of order of operations worksheets. The more practice a student gets, the better. For example you can physically separate word problems from the answer choices in the classroom. Students would have to walk around to discuss and solve the problem and then find the answer that matches.
- Students could be given an expression without the symbols. They would have to then decide which operations/symbols would make the expression true.
Easy mistakes to make
- Multiplication/division and addition/subtraction in the incorrect order
When you have a chain of multiplication and division calculations or a chain of addition and subtraction calculations, you work from left to right.
For example, If you put parentheses into the calculation 12\div{4}\times{3} with the purpose of keeping the calculation exactly the same, you must place the parentheses around 12\div{4}.
This is because 12\div{4}\times{3}=9, and (12\div{4})\times{3}=3\times{3}=9.
If you placed parentheses around 4\times{3} you would have 12\div{(4\times{3})}=12\div{12}=1 which is a different answer that you would get without the parenthesis.
- Exponents as multiplying a number by 2
When introducing exponents, some students will interpret 4^2 as 4 \times 2 instead of 4 \times 4. The use of a number line to represent this expression or using expanded notation when introducing the concept can help students internalize the learning.
- Multiplying before exponents
Take 2\times{3}^{4}. Because you would perform exponents before you perform multiplication within PEMDAS, you need to calculate the exponent term first, and then multiply the solution by 2. Inserting a pair of parentheses with the purpose of keeping the calculation exactly the same, 2\times{3}^{4}=2\times(3^{4})=162. A common misconception is that the multiplication is carried out first, and then the value is raised to the power; here this would look like (2\times{3})^{4} and is equal to 6^{4}=1296 which is the wrong answer.
Related properties of equality lessons
Practice order of operations questions
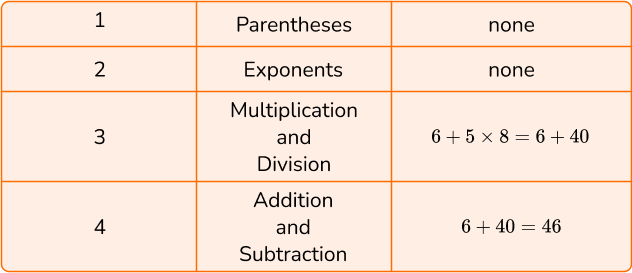
1. Calculate 6+5 \times 8.




To solve, follow the order of operations by using PEMDAS.
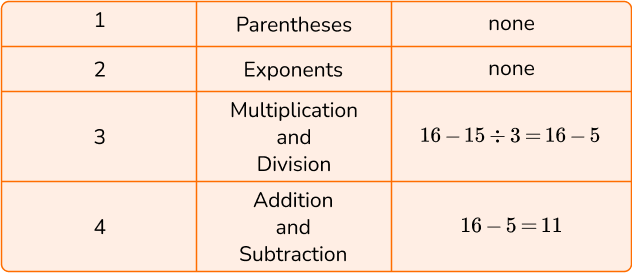
2. Calculate 16-15 \div 3.




To solve, follow the order of operations by using PEMDAS.
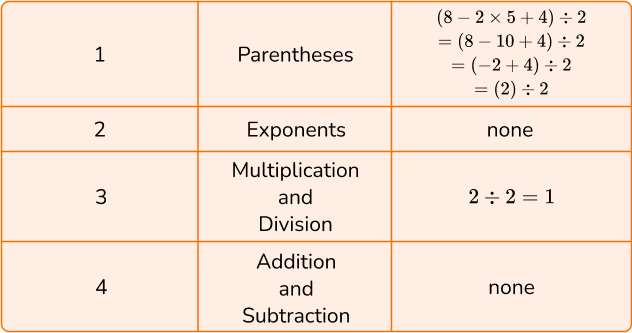
3. Calculate (8-2 \times 5+4) \div 2.




To solve, follow the order of operations by using PEMDAS.
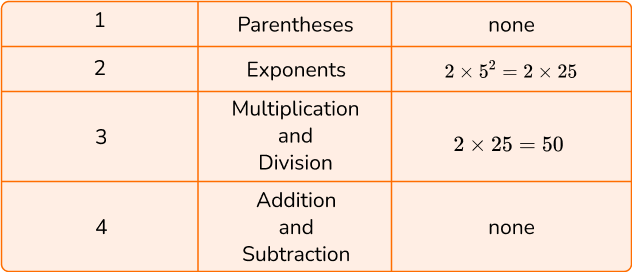
4. Calculate 2 \times 5^2.




To solve, follow the order of operations by using PEMDAS.
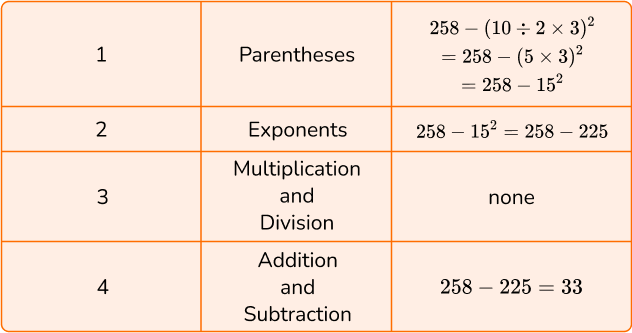
5. Calculate 258-(10 \div 2 \times 3)^2.




To solve, follow the order of operations by using PEMDAS.
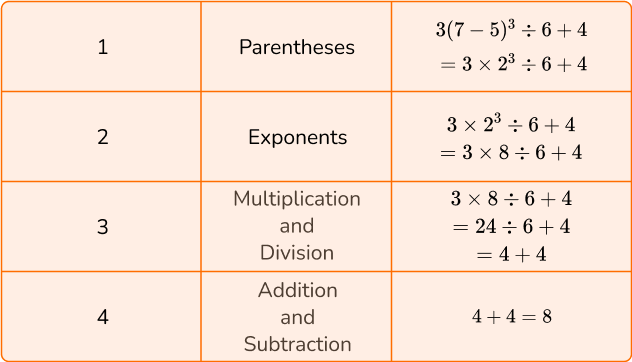
6. Calculate 3(7-5)^3 \div 6+4.




To solve, follow the order of operations by using PEMDAS.
Order of operations FAQs
In the order of operations, multiplication and division are seen as equal and would be performed as they are stated within the expression, starting from left to right. The same is true with addition and subtraction.
Both PEMDAS and BODMAS are correct. The acronym BODMAS is the UK version of the same rules. It can also be referred to as BIDMAS or BEDMAS. The acronym in the UK would read as: Brackets, Indices, Division and Multiplication, Addition and Subtraction.
An exponent refers to the number of times a number is multiplied by itself. For example 7^2 = 7 \times 7 or 4^3 = 4 \times 4 \times 4.
Parentheses are used within mathematical expressions to note a modification is the normal order of operations. In the expression, (3+4) \times 3, because the addition is within parentheses, it is solved before the multiplication.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!