High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Area of a triangle Hypotenuse Trig functions Rounding decimals Significant figures Pythagorean Theorem Square rootsTrig formula for area of a triangle
Here you will learn about the trig formula for area of a triangle, including how to generate the formula, use the formula to find the area of a triangle, and apply this formula to other polygons.
Students will first learn about the trig formula for the area of a triangle as part of geometry in high school.
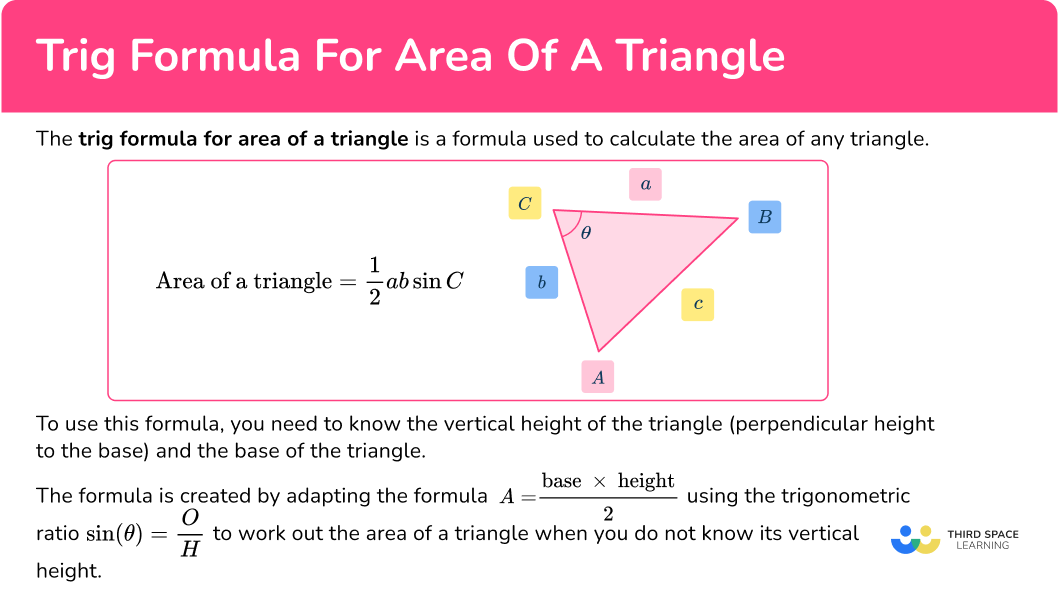
What is the trig formula for area of a triangle?
The trig formula for area of a triangle is a formula used to calculate the area of any triangle.
Area of a triangle =\cfrac{1}{2} \, ab\sin{C}
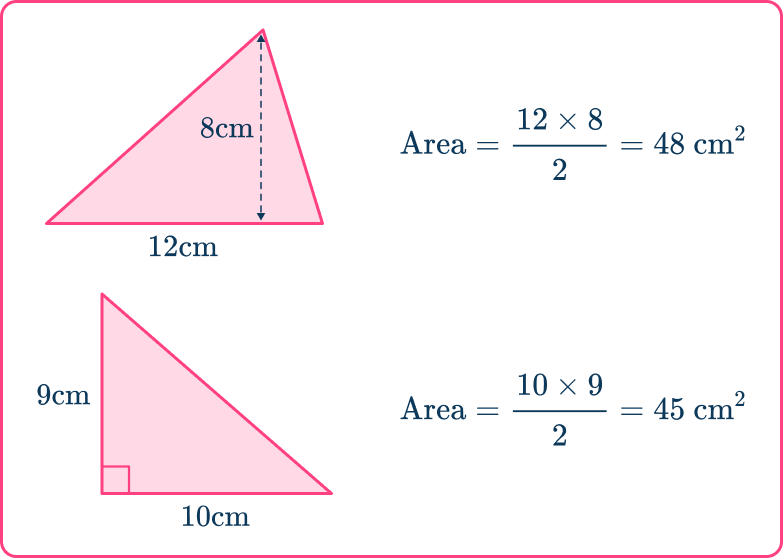
Previously, you have calculated the area of a triangle using the area formula
Area of a triangle =\cfrac{\text{base }\times\text{ height}}{2}
To use this, you need to know the vertical height of the triangle (perpendicular height to the base) and the base of the triangle.
You can adapt this formula using the trigonometric ratio \sin(\theta)=\cfrac{O}{H} to work out the area of a triangle when you do not know its vertical height. The formula you get is:
Area of a triangle =\cfrac{1}{2} \, ab\sin{C}
The triangle should be labeled as follows, with the lower case letter for each side opposite the corresponding upper case letter for the angle.
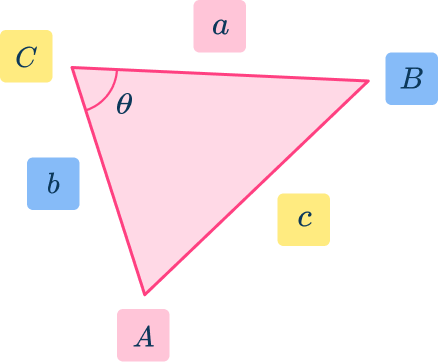
You need to know
- the length of at least 2 sides of a triangle
- the included angle between these two sides.
For example, triangle ABC has been labeled where C is the included angle between the two sides of the triangle a and b.
What is the trig formula for area of a triangle?
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Worksheet (Grade 9 to 12)
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
[FREE] Trigonometry Worksheet (Grade 9 to 12)
![[FREE] Trigonometry Worksheet (Grade 9 to 12)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Trigonometry-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 9 to 12 students’ understanding of Trigonometry. 15+ questions with answers covering a range of 9th to 12th grade trigonometry topics to identify areas of strength and support!
DOWNLOAD FREEWhich area of a triangle formula should I use?
If you know or can work out the vertical height of a triangle, it can be easier to use
Area of a triangle =\cfrac{\text{base }\times\text{ height}}{2}.
For example,
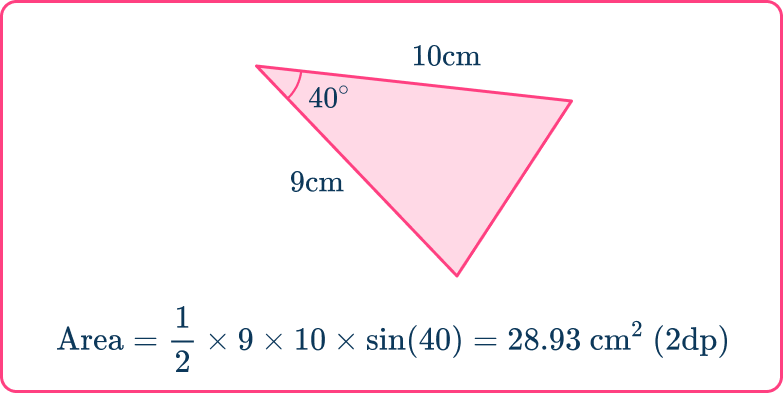
However, if the vertical height is not labeled and there are two given sides and the angle in between, you would need to use
Area of a triangle =\cfrac{1}{2} \, ab\sin{C}
Once you know which formula to use, you need to substitute the correct values into it and then solve the equation to calculate the area.
The area is always written with square units.
Remember: other polygons can be split into triangles to find the interior angles, so the formula for the area of a triangle \left(A=\cfrac{1}{2} \, ab\sin{C}\right) can be applied to find the area of a rectangle, the area of an equilateral triangle, the area of a pentagon, or the area of a parallelogram etc.
Common Core State Standards
How does this relate to high school math?
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.D.9)
Derive the formula A=\cfrac{1}{2} \, ab\sin{C} for the area of a triangle by drawing an auxiliary line from a vertex perpendicular to the opposite side.
How to use the trig formula for area of a triangle
In order to use the trig formula for area of a triangle:
- Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} . - Substitute the given values into the formula, Area =\bf{\cfrac{1}{2}} \, \textbf{ab} \, \bf{\sin} \, \textbf{{C}}.
- Solve the equation.
Trig formula for area of a triangle examples
Example 1: with two sides and the angle in between
Calculate the area of the triangle ABC. Write your answer to the nearest hundredth.
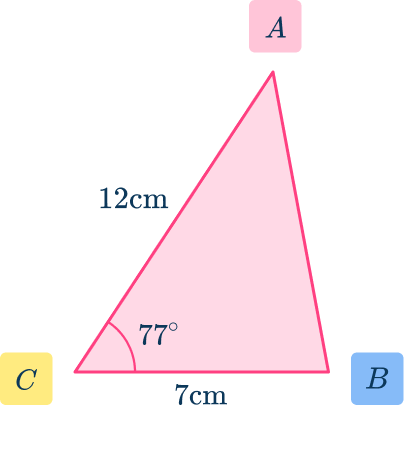
- Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Remember that angles are capitalized and the side opposite each angle is the respective lower case letter (for example, side a is opposite angle A ).
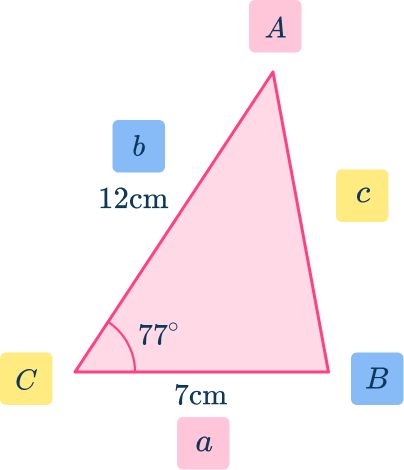
2Substitute the given values into the formula.
\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2}\times{7}\times{12}\times\sin(77) \end{aligned}3Solve the equation.
A=42\times\sin(77)=40.92\mathrm{~cm}^{2}\text{ (2dp)}.Example 2: with two sides and the angle in between
Calculate the area of the triangle. Write your answer to the nearest hundredth.
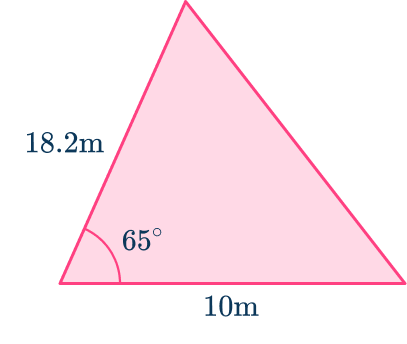
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Here, you label each side a, \, b, and c and each vertex A, \, B and C .
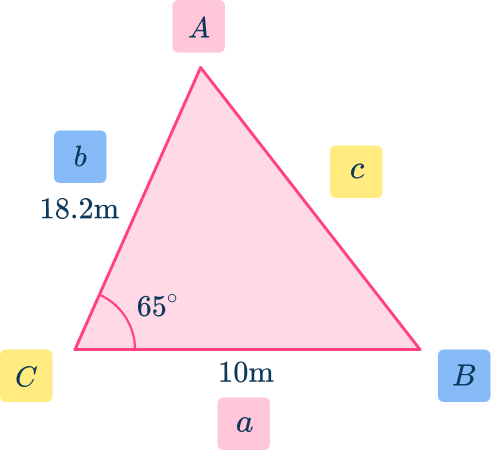
Substitute the given values into the formula
Solve the equation.
Example 3: with three sides and one angle
Calculate the area of the scalene triangle PQR. Write your answer to 3 significant figures.
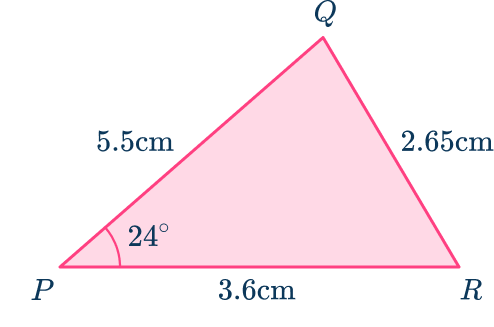
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Here, you label each side and each angle. You could do this in an alternative color pen.
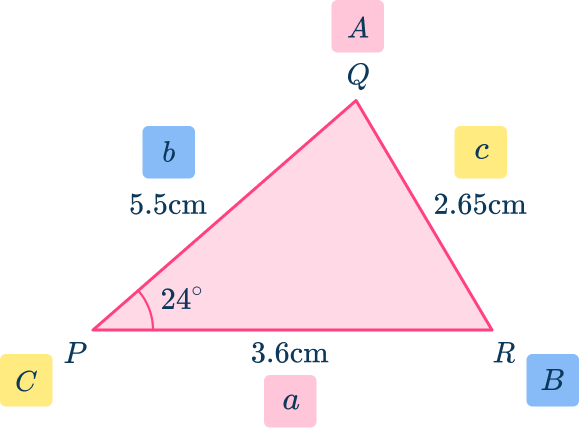
Substitute the given values into the formula
Solve the equation.
Example 4: area of an isosceles triangle with a known angle
Triangle XYZ is an isosceles triangle. Find the area of the triangle to the nearest hundredth.
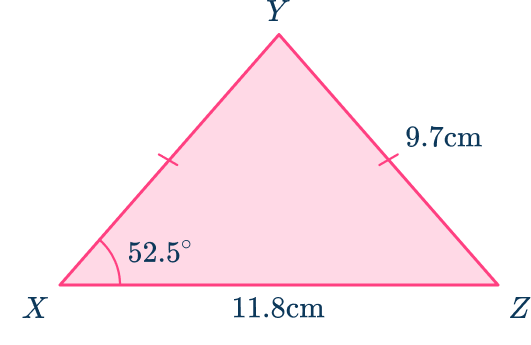
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Here, you label each side and each angle.
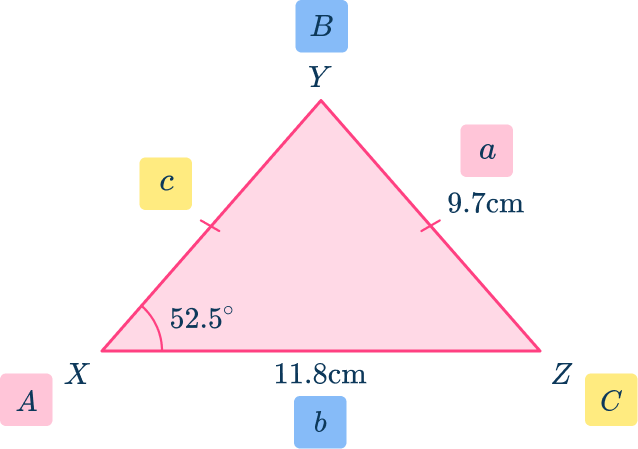
Substitute the given values into the formula
As triangle XYZ is isosceles, a=c=9.7\mathrm{~cm} and angle C= angle A=52.5^{\circ}.
\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2}\times{9.7}\times{11.8}\times\sin(52.5) \end{aligned}
Solve the equation.
Example 5: with two sides and two angles
Calculate the area of the triangle ABC. Write your answer to the nearest hundredth.
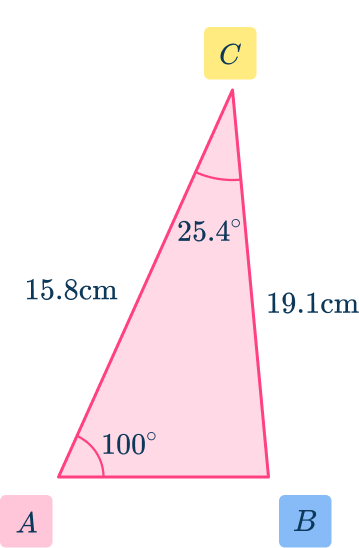
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Here, you label 25.4^{\circ} as C as this angle is between two known sides.
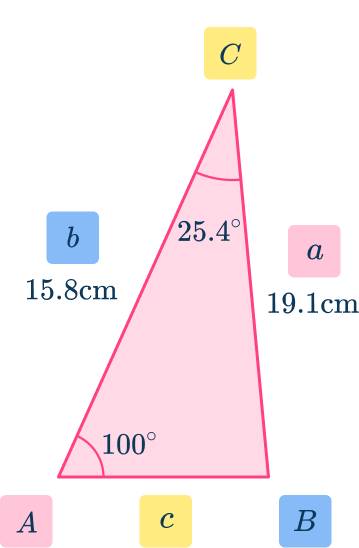
Substitute the given values into the formula
Solve the equation.
Example 6: with two sides and two angles
Calculate the area of the triangle ABC. Write your answer to 4 significant figures.
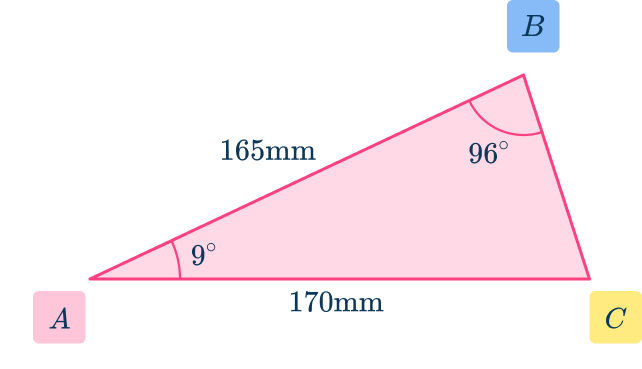
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
Here, you have to think carefully before Step 2 because a, \, b, and C do not correspond to a, \, b and C in A=\cfrac{1}{2} \, ab\sin{C}.
As the known sides b and c have the included angle at A with all three values known, you can adjust the area of a triangle using sine to make A=\cfrac{1}{2} \, bc\sin{A} .
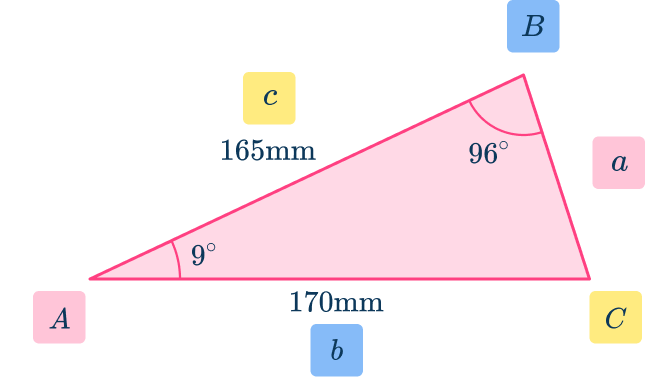
Substitute the given values into the formula.
Solve the equation.
Example 7: finding a length given the area
The area of this triangle is 30 \, cm^2. Find the length labeled x.
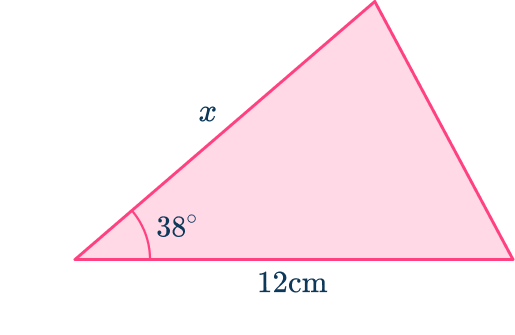
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
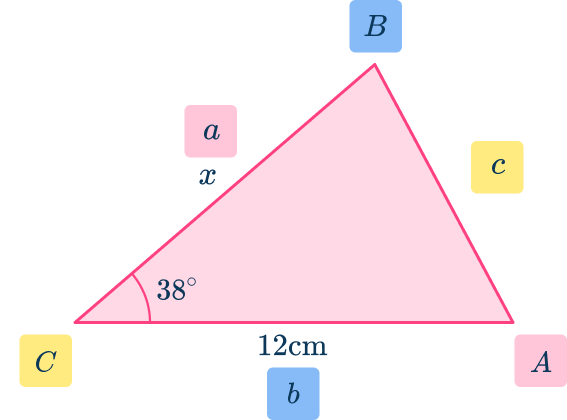
Substitute the given values into the formula
This time, you know the area and are calculating the missing side a.
\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ 30&=\cfrac{1}{2}\times{x}\times{12}\times\sin(38) \end{aligned}
Solve the equation.
Example 8: finding an angle given the area
The area of this triangle is 42 \, cm^2. Find the angle labeled x.
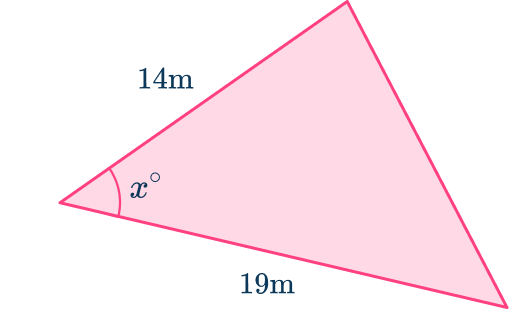
Label the angle you are going to use angle \textbf{C} and its opposite side \textbf{c} .
Label the other two angles \textbf{A} and \textbf{B} and their corresponding sides \textbf{a} and \textbf{b} .
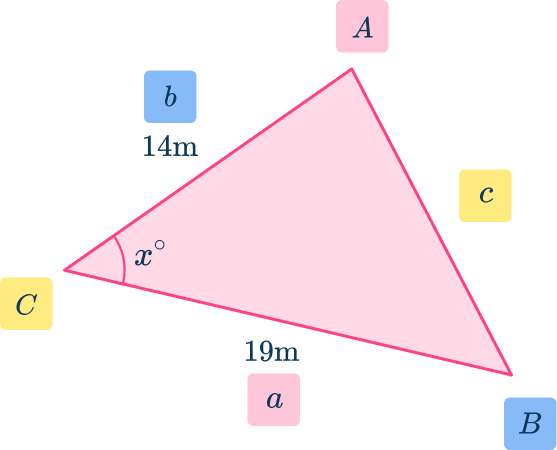
Substitute the given values into the formula.
This time, you know the area and are calculating the missing angle x.
\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ 42&=\cfrac{1}{2}\times{19}\times{14}\times\sin(x) \end{aligned}
Solve the equation.
Teaching tips for trig formula for area of a triangle
- Begin with the basic formula for the area of a triangle (halving the base times height): \text{Area }=\cfrac{1}{2}\times\text{ base }\times{height}. Explain that when the height is not directly given, we can use trigonometric functions, specifically \sin(C), to calculate it.
- Introduce Heron’s formula for the area of a triangle when all three sides are known:
\text{Area }=\sqrt{s(s-a)(s-b)(s-c)}
where s=\cfrac{a+b+c}{2} is the semi-perimeter.
Discuss when each formula is most appropriate:- Use Heron’s formula when the lengths of all three sides are known.
- Use \cfrac{1}{2} absinC when two sides and the included angle are given.
Easy mistakes to make
- Forgetting to use sine for the angle
Some students may substitute the angle C directly into the formula instead of finding \sin(C). Remember that \sin(C) is the sine function of the angle, not the angle itself. Use a calculator or table to compute it.
- Confusing different formulas
Understand when to use each formula. Use \cfrac{1}{2} absinC specifically when you have two sides and the included angle.
- Using degrees when the angle is in radians (or vice versa)
Check the calculator mode (DEG or RAD) and ensure it matches the given angle’s unit.
Related trigonometry lessons
Practice trig formula for area of a triangle questions
1. Calculate the area of the right angle triangle.
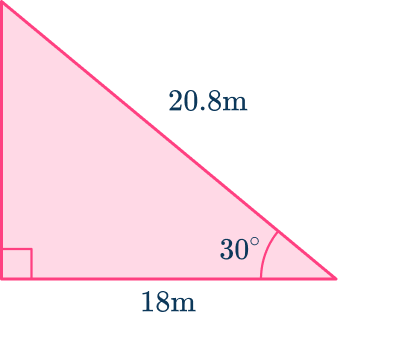




Label the triangle:
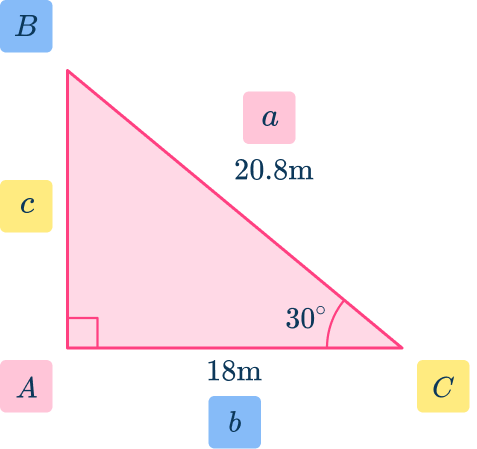
\begin{aligned}\text{Area }&=\cfrac{1}{2} \, ab\sin(C) \\\\ &=\cfrac{1}{2}\times{20.8}\times{18}\times\sin(30) \\\\ &=93.6\mathrm{~m}^{2} \end{aligned}
2. Calculate the area of the triangle, correct to the nearest hundredth.
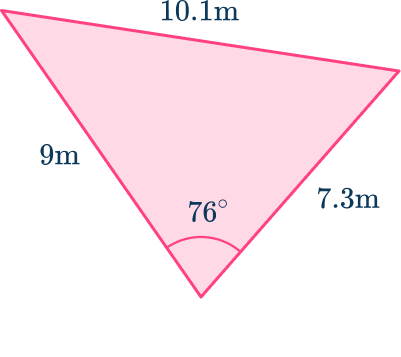




Label the triangle:
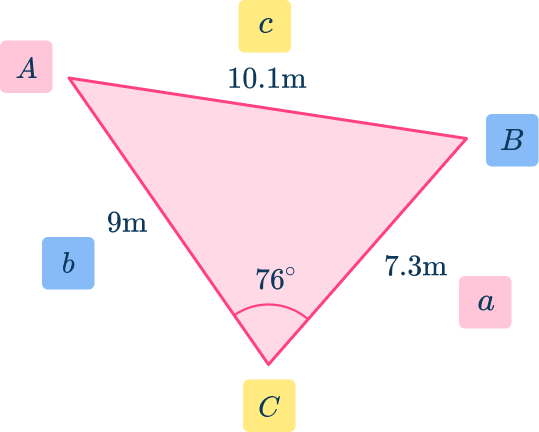
\begin{aligned}\text{Area }&=\cfrac{1}{2} \, ab\sin(C) \\\\ &=\cfrac{1}{2}\times{7.3}\times{9}\times\sin(76) \\\\ &=31.87\mathrm{~m}^{2} \end{aligned}
3. Calculate the area of the equilateral triangle XYZ. Write your answer to the nearest hundredth.
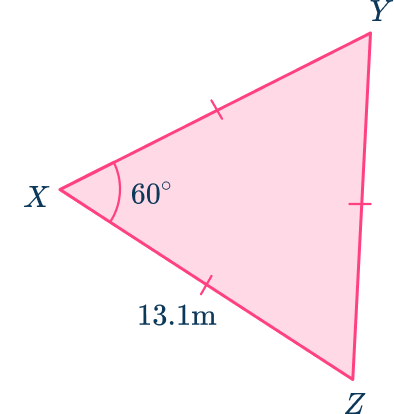




Label the triangle:
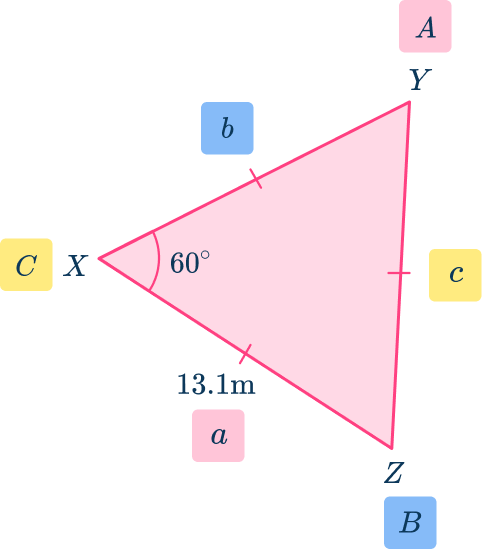
\begin{aligned}\text{Area }&=\cfrac{1}{2} \, ab \sin(C) \\\\ &=\cfrac{1}{2}\times{13.1}\times{13.1}\times\sin(60) \\\\ &=74.31\mathrm{~m}^{2}\end{aligned}
4. Calculate the area of the parallelogram, correct to the nearest hundredth.
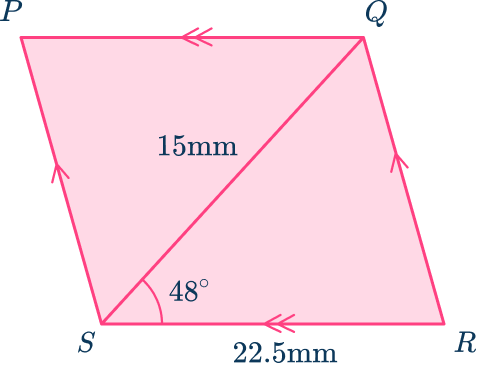




You need to look at the two triangles individually. The triangles are congruent (exactly the same) since all three of the lengths of the sides are equal (SSS). Therefore you can calculate the area of one triangle and then double it.
Label one triangle:
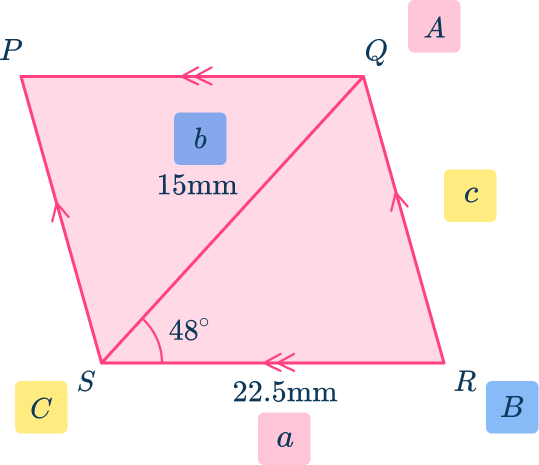
\begin{aligned}\text{Area }&=\cfrac{1}{2} \, ab\sin(C) \\\\ &=\cfrac{1}{2}\times{22.5}\times{15}\times\sin(48) \\\\ &=125.406\mathrm{~mm}^{2} \\\\ \text{Total area }&={2}\times{125.406}\\\\ &=250.81\mathrm{~mm}^{2} \end{aligned}
5. Calculate the area of the isosceles triangle PQR, correct to 3 significant figures.
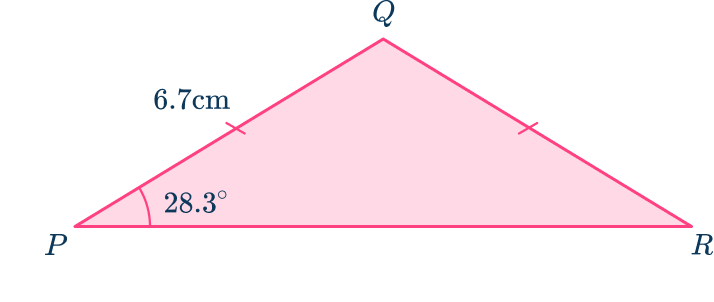




First, calculate angle PQR\text{:} \, 180-28.3-28.3=123.4^{\circ}
Then label the triangle:
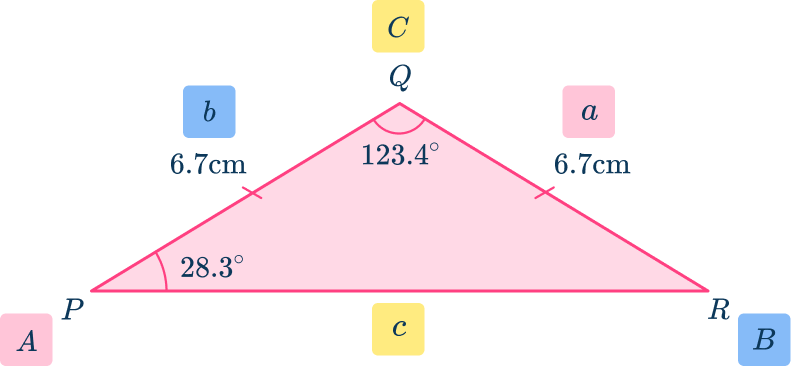
\begin{aligned}\text{Area }&=\cfrac{1}{2} \, ab \sin(C) \\\\ &=\cfrac{1}{2}\times{6.7}\times{6.7}\times\sin(123.4) \\\\ &=18.7\mathrm{~cm}^{2} \end{aligned}
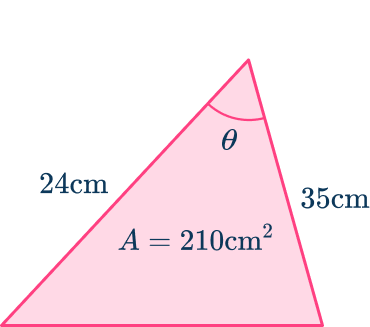
6. Calculate the value of \theta.




Trig formula for area of a triangle FAQs
You can find the area of a triangle using trigonometry by using the trig formula for area of a triangle: Area =\cfrac{1}{2} \, ab\sin{C}
This formula is useful when:
◦ You know the lengths of two sides of a triangle and the measure of the angle between them.
◦ The height of the triangle isn’t directly provided but can be calculated using trigonometry.
It works because:
◦ The basic formula for the area of a triangle is \cfrac{1}{2} \text{ base }\times\text{ height} .
◦ Using trigonometry, the height can be expressed as b\sin{C} when one side acts as the base and the other forms the hypotenuse of a right triangle with the height as the perpendicular.
You should use this formula when:
◦ You know two sides and the included angle of a triangle.
◦ The triangle is not a right triangle, and the height is not explicitly given.
The next lessons are
- Circle math
- Angles of a circle
- Circle theorems
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!