High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Parts of a circle Congruent shapes Right triangle Isosceles triangle Pythagorean TheoremCircle chord theorems
Here you will learn about circle theorems involving the chords of a circle and the relationships they create. You will learn the application of these theorems, the proofs of these theorems, and how to use them to solve more complex problems.
Students first learn how to work with these circle theorems in a geometry course where they spend a time delving into the proofs and application. Circle theorems are essential for success on graduation assessments as well as college entrance assessments.
What are circle chord theorems?
Chord circle theorems are geometrical properties of circles that can be calculated using the chord of a circle. The chord of a circle is a line segment that connects two points that sit on the edge of a circle. The longest chord in a circle is the diameter of the circle.
Recall the parts of a circle that are essential to understand circle chord theorems.

- The diameter of the circle is the width of a circle, through the center. The endpoints of the diameter lie on the circumference of the circle. The diameter is twice the length of the radius of the circle.
- An arc is a part of the circumference.
- The major segment is the larger part of a circle when it is enclosed by a chord and the major arc.
- The minor segment is the smaller part of a circle when it is cut by a chord and the minor arc.
- The radius of a circle is the distance between the center of the circle and the circumference of the circle.
Let’s take a look at the first circle theorem.
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREE![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
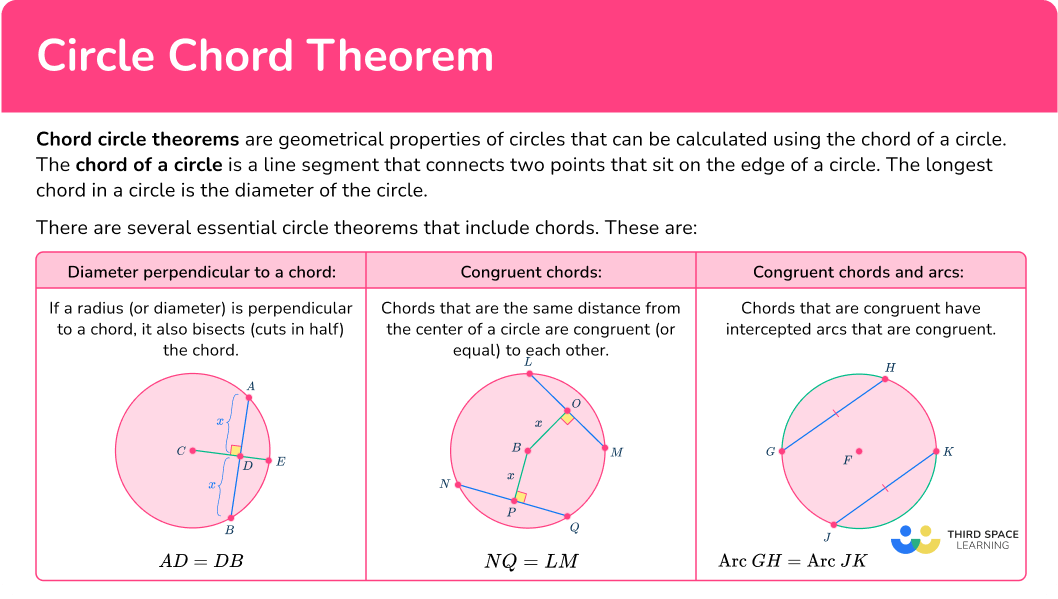
DOWNLOAD FREE1) Diameter perpendicular to a chord
The perpendicular from the center of a circle to a chord bisects the chord (splits the chord into two equal parts).
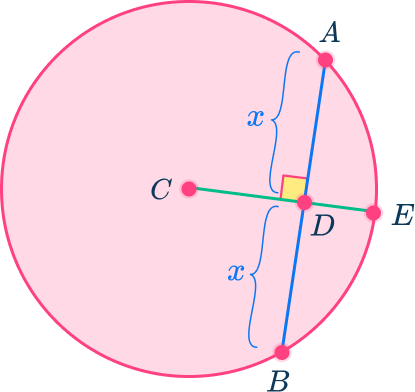
In the diagram above, AB is a chord and CE is a radius (half the diameter).
Here we can see that the radius CE bisects the chord AB at 90 degrees and the lengths AD=BD=x
You can use congruent triangles to prove this is always true.
First, draw two radii, AC and BC, to make two right triangles, triangle ADC and triangle BDC.
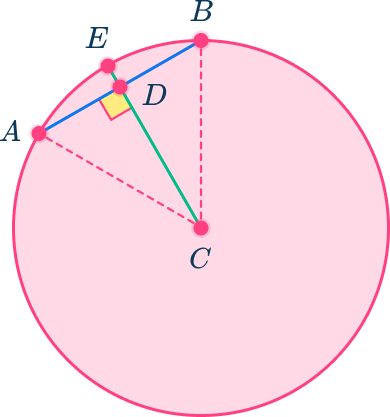
Since radii within a circle are congruent in length, you know that the hypotenuses of both triangles are congruent.
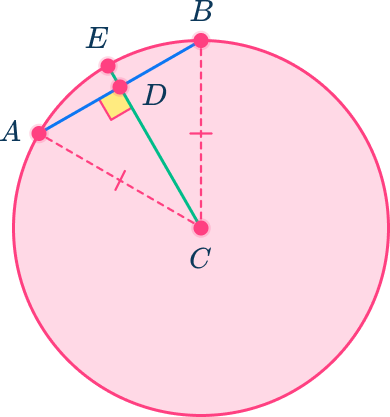
Since both triangles share side CD, through the reflexive property, CD is congruent to itself.
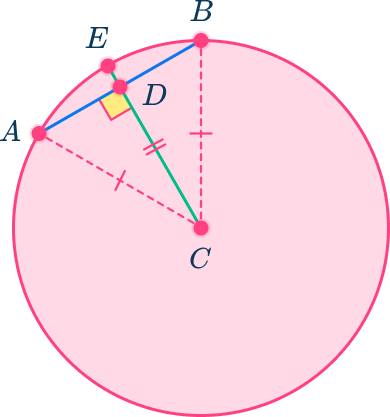
Therefore, using the triangle congruence theorem of Hypotenuse-Leg, you can conclude that triangle ADC is congruent to triangle BDC.
Since the two triangles are congruent, you can further conclude through the definition of congruent triangles that AD is congruent to BD.
This proves that when the diameter (or radius) is perpendicular to a chord, it also bisects (cuts in half) the chord.
2) Congruent chords
Chords in a circle are congruent if and only if they are the same distance from the center of the circle.
In circle B, BO and BP are the same length, x units.
Therefore, chord LM and chord NQ are congruent because they are the same perpendicular distance from the center of the circle.
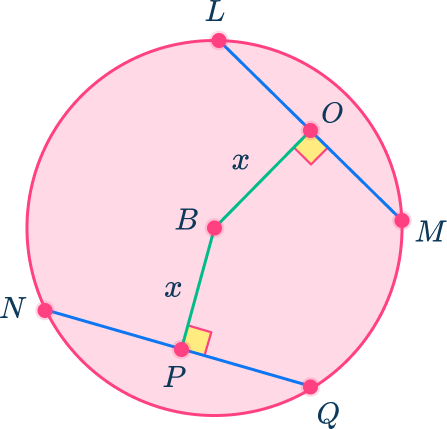
Again, you can use congruent triangles to prove this is true.
First, sketch in the radii to create two triangles. All the radii within the same circle are congruent. Triangle LBM and triangle NBQ are isosceles triangles.
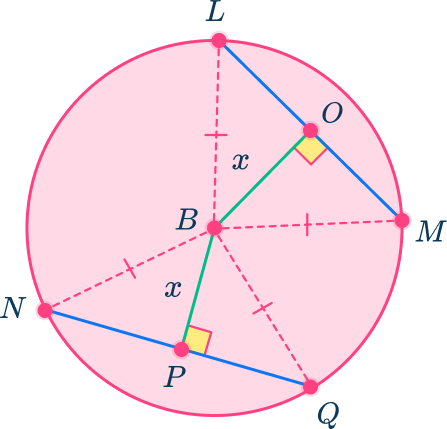
Using the Isosceles triangle theorem, you know that opposite congruent sides of a triangle are congruent angles.

Angle BNQ is congruent to angle BQN. Also, angle BML is congruent to angle BLM.
Since BN is congruent to BQ which is congruent to BM which is congruent to BL, you can conclude that angle BNQ is congruent to angle BQN which is congruent to angle BML which is congruent to angle BLM.
Hence, using the Angle-Angle-Side triangle congruent theorem, you can conclude that triangle NBQ is congruent to triangle LBM.
Since the triangles are congruent, then using the definition of congruent triangles, you can conclude that side NQ is congruent to side LM.
3) Congruent chords and intercepted arcs
When two chords in a circle are congruent, the arcs they intercept are congruent.
If chord JK is congruent to chord GH, then arc JK is congruent to arc GH.
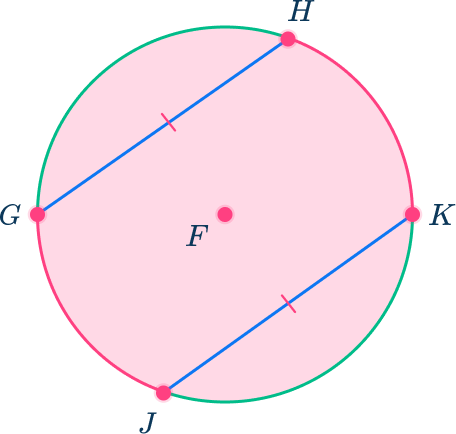
You can use central angles to prove this is true.
First, draw in two diameters.
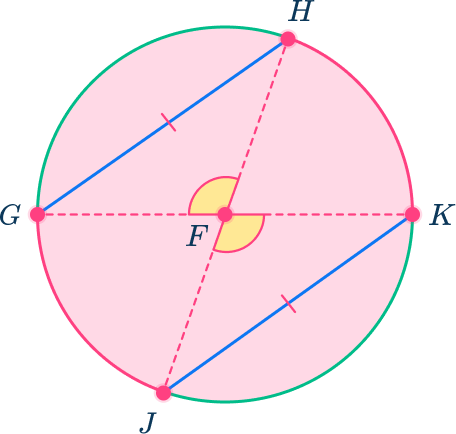
The diameters create central angles. Central angle GFH is congruent to angle JFK because they are vertical angles.
Angle GFH intercepts arc GH and angle JFK intercepts arc JK.
Since angle GFH is congruent to angle JFK, you can conclude that arc GH is congruent to arc JK because central angles are equal in measure to the arcs they intercept.
Likewise, angle GFJ is congruent to angle HFK because they are vertical angles. So, arc GJ must be congruent to arc HK.
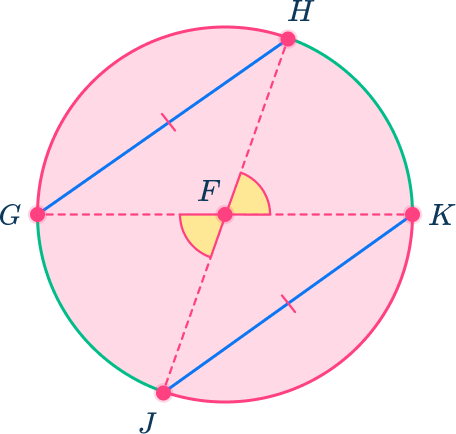
Note that for this example, the two arcs GH and JK are parallel. If they are not parallel, the proof would be similar to that for “(2) Congruent Chords ”.
Subtended angles
An angle within a circle is created by two chords meeting at a point on the circumference. The diagrams below show the inscribed angle subtended by arc AC from point B for two different circles.
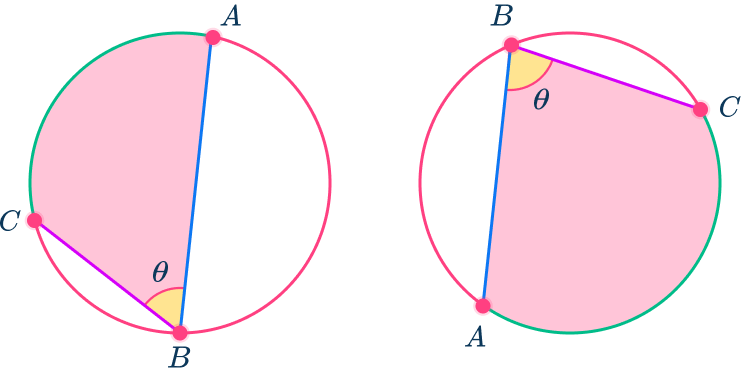
Top tip: The word subtend is used a lot within circle theorems so make sure you know what it means.
What are circle chord theorems?
Common Core State Standards
How does this apply to geometry?
- High School Geometry – Circles (HSG-C.A.2)
Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle.
How to use circle chord theorems to solve problems
In order to find missing angles or the length of a chord:
- Identify the key parts of the circle that are given.
- Apply the appropriate theorem to problem solve.
- Describe or create an equation to find the missing part.
- Find the solution.
Circle chord theorems examples
Example 1:
In circle C, DK is perpendicular to GH. If GH is 26 units, find HJ.
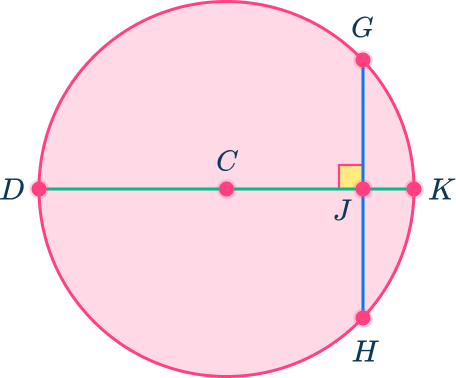
- Identify the key parts of the circle that are given.
Since C is the center of the circle, DK is the diameter, which means that CK is the radius.
GH is a chord that has a length of 26 units.
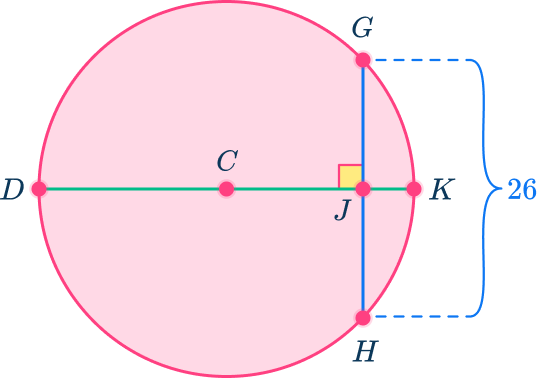
2Apply the appropriate theorem to problem solve.
Using the theorem that if the diameter or radius is perpendicular to a chord, then it bisects the chord – meaning it cuts the chord into two equal halves. So, the diameter is the perpendicular bisector of a chord.
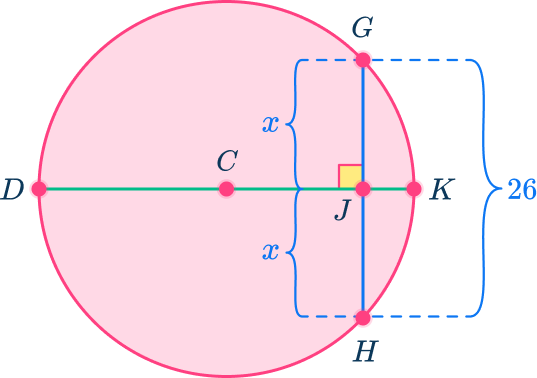
3Describe or create an equation to find the missing part.
In this case, divide 26 by 2 or multiply it to \cfrac{1}{2}.
26\div{2}=13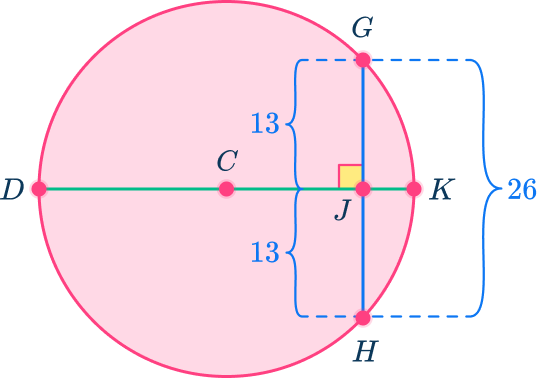
4Find the solution.
HJ=13 units
Example 2: triangle
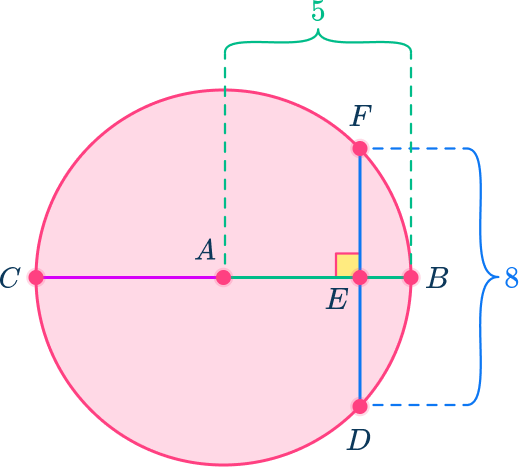
In circle A, diameter BC is perpendicular to DF. DF is equal to 8 and BC=10, find the length of BE.
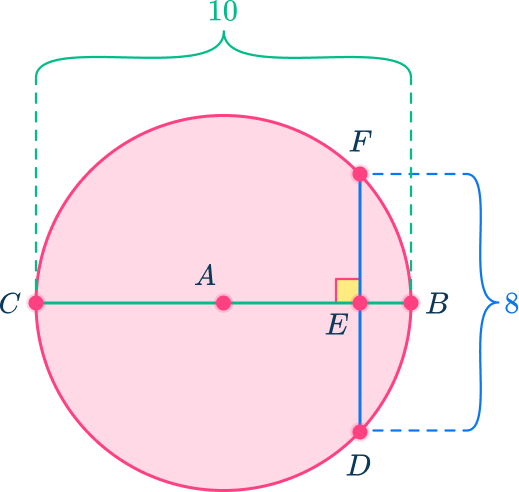
Identify the key parts of the circle that are given.
Diameter BC is perpendicular to chord DF so DF is also being bisected by BC. AB and AC are radii of the circle. As the radius of any circle is half the length of the diameter, AB=AC=5.
Apply the appropriate theorem to problem solve.
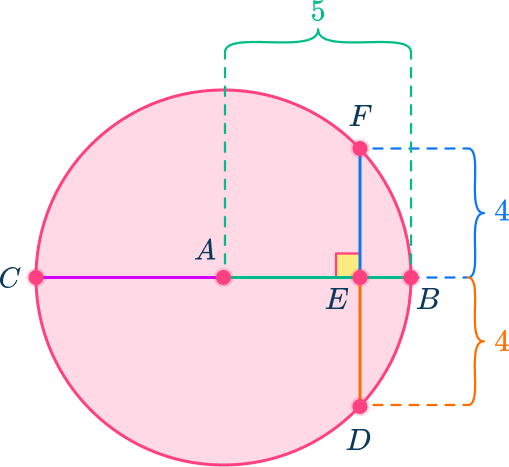
Using the theorem that if the diameter or radius is perpendicular to a chord, then it bisects the chord – meaning it cuts the chord into two equal halves.
DE=EF=8\div{2}=4
Describe or create an equation to find the missing part.
In this case, draw in another radius to create a right triangle AEF.
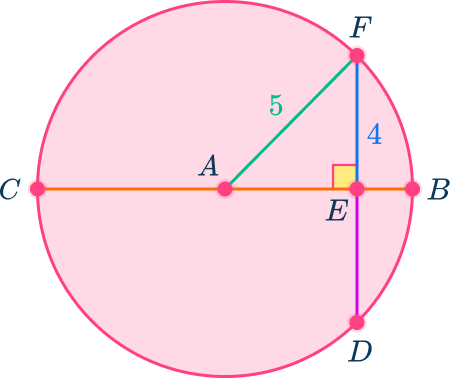
The radius is the hypotenuse of the triangle, AF=5.
EF is one of the legs of the right triangle, EF=4.
Since it is a right triangle, use the Pythagorean Theorem (a^{2}+b^{2}=c^{2}), find the missing leg, AE.
Find the solution.
Let AE=a, EF=b=4, and AF=c=5 (remember c is always the hypotenuse of a right triangle).
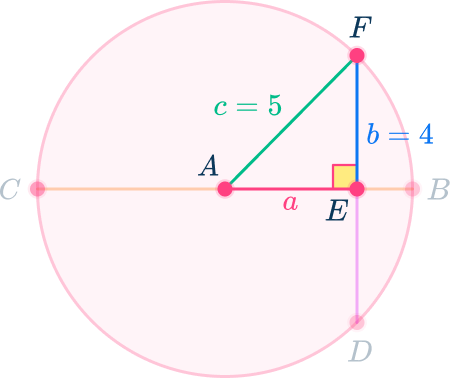
Then,
\begin{aligned} a^{2}+4^{2}&=5^{2} \\\\ a^{2}+16&=25 \\\\ a^{2}&=25-16=9 \\\\ a&=\sqrt{9}=3 \end{aligned}
So, AE=3 units.
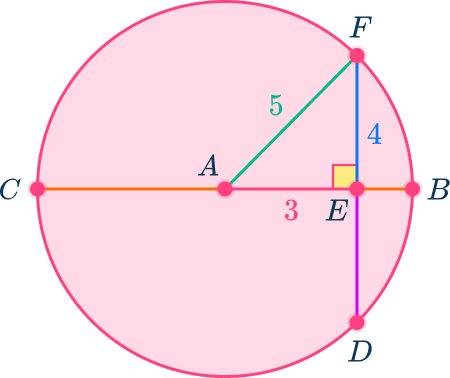
Since the radius AB is 5 units, subtract AE from AB to find BE,
AB-AE=5-3=2.
BE=2 units.

Example 3: arcs
In circle B, chord LM is congruent to chord KN.
Minor arc LM=5x-2
Minor arc KN=3x+14
Find the measure of Minor arc KN.
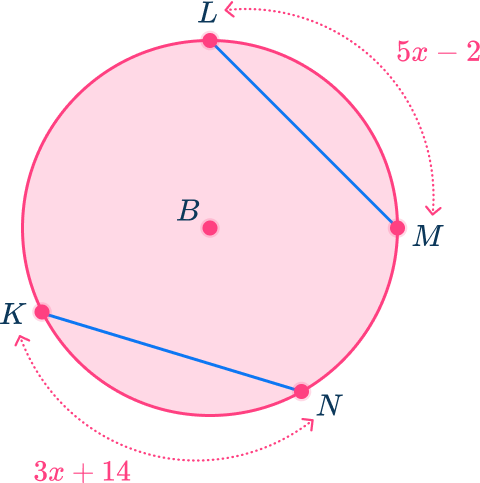
Identify the key parts of the circle that are given.
In circle B, chord LM intercepts minor arc LM and chord KN intercept minor arc KN.
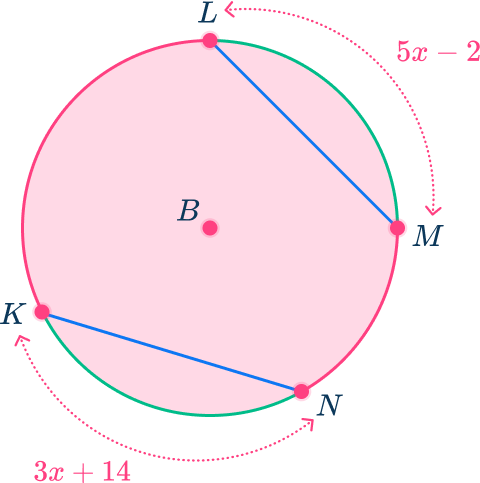
Apply the appropriate theorem to problem solve.
Using the theorem that congruent chords intercept congruent arcs, minor arc KN is congruent to minor arc LM.
Describe or create an equation to find the missing part.
As the chords are congruent, the arcs are congruent (the same length), so
5x-2=3x+14
Find the solution.
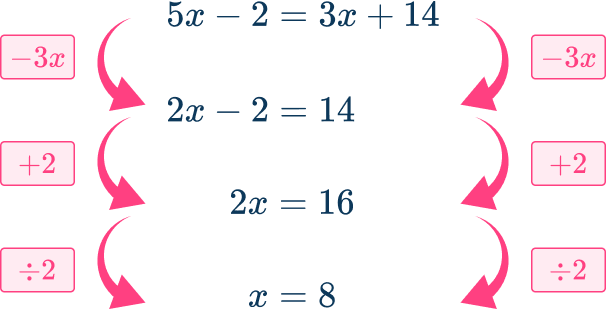
Substitute x=8 into 3x+14 to find the length of arc KN\text{:}
Arc KN=3(8)+14=38 units
Example 4:
In circle M, LK is the diameter and perpendicular to PR. If RS=7x-3 and PS=3x+17, find PR.
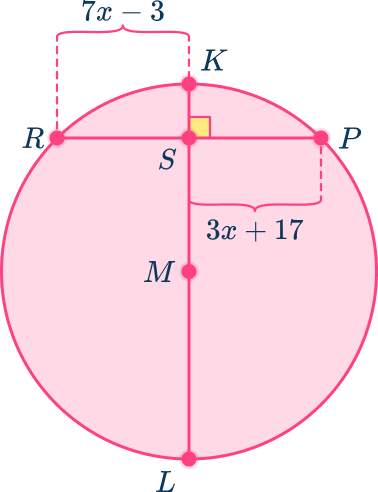
Identify the key parts of the circle that are given.
In circle M, KL is a diameter and is perpendicular to PR. \; KM is a radius of circle M.
RS=7x-3
PS=3x+17

Apply the appropriate theorem to problem solve.
Using the theorem that if the diameter or radius is perpendicular to a chord, then it bisects the chord – meaning it cuts the chord into two equal halves. This means that RS=PS.
Describe or create an equation to find the missing part.
As RS=PS, form the equation
7x-3=3x+17
Find the solution.
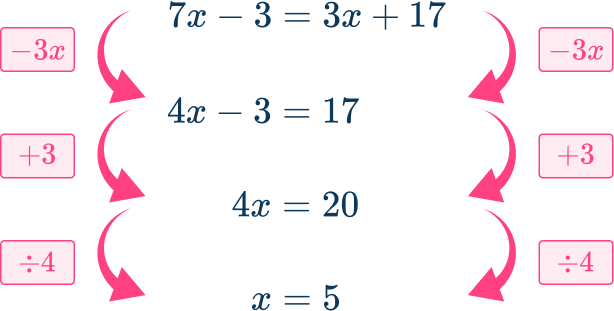
Substitute x=5 into 7x-3 to find the measure of RS:
RS=7(5)-3=32
Substitute x=5 into 3x+17 to find the measure of PS\text{:}
PS=3(5)+17=32
Find the sum of RS and PS to find the measure of PR:
PR=RS+PS=32+32=64 units
Example 5:
In circle L,
- QU=5a
- Chord ST=60
- LU=LW=4 units
- Angle LWT= Angle LUQ=90^{\circ}.
Find the value of a.
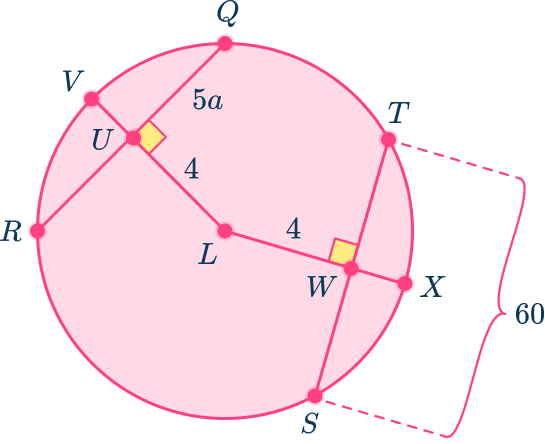
Identify the key parts of the circle that are given.
Chord ST=60
LU=LW=4
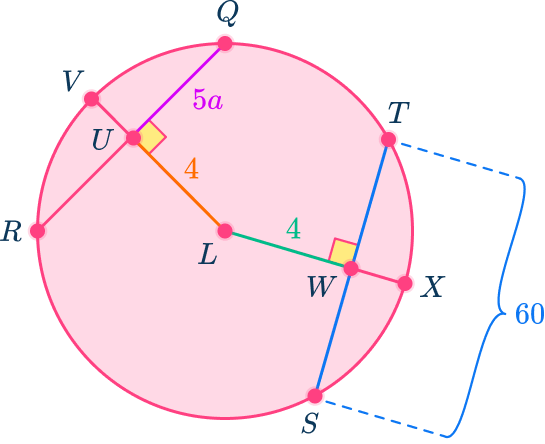
Apply the appropriate theorem to problem solve.
Since chord ST and chord QR are the same distance from the center of the circle, they are congruent to each other. This means that QR=ST.
LU is perpendicular to QR so QU is half the length of QR.
As QR=ST, QU is half the length of ST.
Describe or create an equation to find the missing part.
As QU=5a and ST=60
5a=\cfrac{1}{2} \times 60
Find the solution.
So, a=6.
Example 6: semicircle
In circle B, minor arc LM and minor arc KN are congruent to each other. Chord LM=x^{2} and chord KN=x+6, find the measure of LM.

Identify the key parts of the circle that are given.
In circle B, minor arc LM is equal/congruent to minor arc KN.
Chord LM=x^2 and chord KN=x+6
Chord LM intercepts arc LM and chord KN intercepts arc KN.
Apply the appropriate theorem to problem solve.
If two arcs are congruent, the chords that intercept the congruent arcs are also congruent.
Describe or create an equation to find the missing part.
Chord KN is the same length as chord LM because they are congruent, so x^{2}=x+6.
Find the solution.
As this is a quadratic, rearrange the quadratic to the general form ax^2+bx+c=0\text{:}
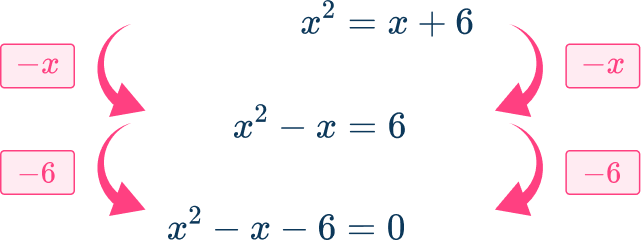
This quadratic can be solved by factorising as b^2-4ac=25
Step-by-step guide: Factoring quadratics
\begin{aligned} &x^{2}-x-6=0\\\\ &(x-3)(x+2)=0\\\\ &x=3\text{ and }x=-2 \end{aligned}
Check the values to see if they work in the original problem. Remember, lengths of chords cannot be negative.
When x=3, LM=x^{2}=3^{2}=9>0.
When x=3, KN=x+6=3+6=9>0.
(LM=KN>0)
When x=-2, LM=x^{2}=(-2)^{2}=4>0
When x=-2, KN=x+6=-2+6=4>0.
(LM=KN>0)
Both values of x work in this case.
Teaching tips for circle chord theorems
- Provide opportunity for students to discover the theorems and make conjectures using compasses and protractors.
- Instead of worksheets, have students use online platforms for game playing to practice skills.
- Incorporate digital platforms such as Desmos for students to explore and investigate the theorems.
Easy mistakes to make
- Forgetting to sketch in a radius to create a triangle
In certain cases, it is helpful to draw in a radius to create a right triangle to find a missing chord length. For example, to find the length EF, it might be helpful to make a right triangle.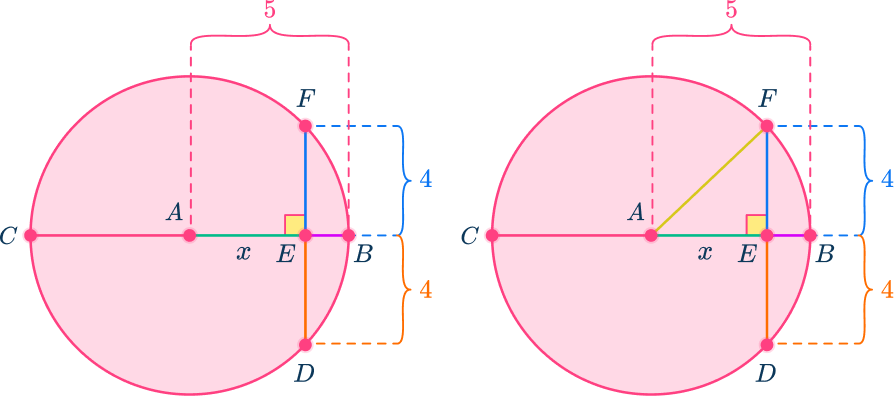
- Not knowing which theorem to apply
Building conceptual understanding of the theorems through constructions helps students to remember and apply the theorems. When problem solving, sometimes you have to apply more than one theorem to solve.
Related circle theorems Lessons
Practice circle chord theorem questions
1. In circle O, minor arc PQ and minor arc MN are 42^{\circ}, chord MN=6x-2 and chord PQ=4x+12.
Find the length of MN.
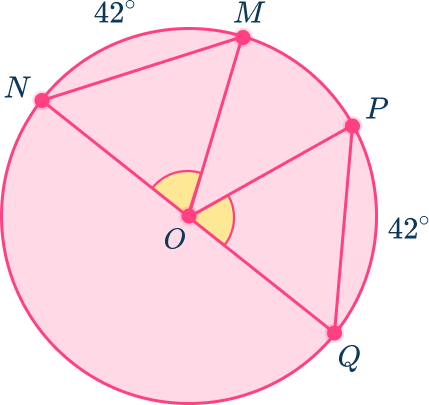
42 units

40 units

7 units

38 units

In circle O, since the arcs are equal in measure, the chords that intercept them are also equal in measure (they are equal chords of a circle).
Chord PQ intercepts arc PQ and chord MN intercepts arc MN.
So, PQ=NM.
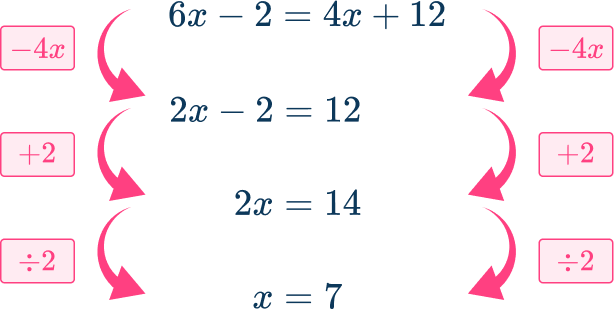
Substitute x=7 into 6x-2 to find the length of LM\text{:}
LM=6x-2=6\times{7}-2=42-2=40 units
2. In circle P, minor arc RS=10x-14 and minor arc TW=6x+22.
Solve for x.





In circle P, chord RS is equal to chord TW, so arc RS has to be equal to arc TW because chord RS intercepts arc RS and chord TW intercepts arc TW.
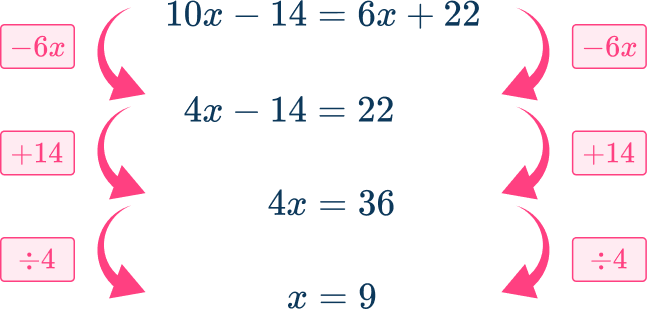
3. In circle C, AG=21. Find BG.
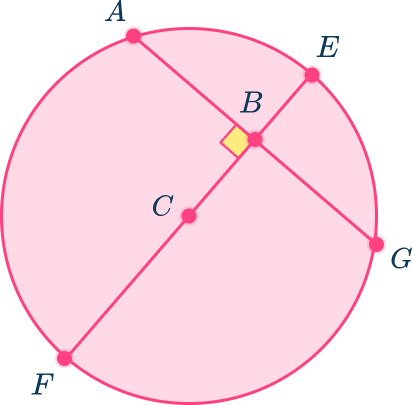
21 units

10 units

11 units

10.5 units

In circle C, EF is the diameter and it is perpendicular to chord AG.
When the diameter of a circle is perpendicular to a chord, it also bisects the chord. So, as AG=21, BG=21 \div 2=10.5 units.
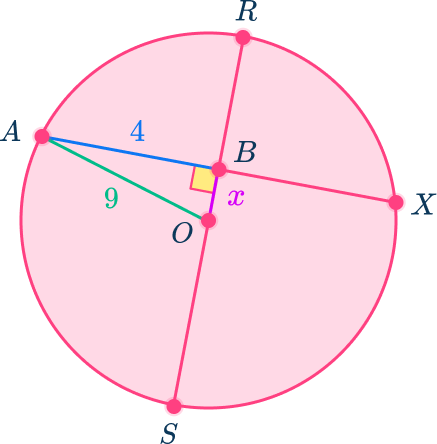
4. In circle O, the diameter is 18 units in length and BX=4 units. Find the length of the chord AX. Round your answer to the nearest tenth.

8.1 units

9 units

16.2 units

8 units

In circle O, since the diameter is perpendicular to chord AX, it bisects chord AX, so AB=BX.
Sketch a right triangle in circle O by drawing in a radius.
Triangle ABO is a right triangle where the hypotenuse of the triangle is the radius of the circle, AO.
Since the diameter is 18 units, the radius is 9 units.
Using Pythagoras’ theorem, you can solve for BO\text{:}
\begin{aligned} 4^{2}+x^{2}&=9^{2}\\\\ 16+x^{2}&=81\\\\ x^{2}&=65\\\\ x&=\sqrt{65}\approx{8.1}\\\\ BO=8.1 \end{aligned}
Since AB=BX, to find AX, multiply 8.1 by 2.
8.1\times{2}=16.2
AX=16.2 units
5. In circle W, find QS if RT=10 and SW=8. Round your answer to the nearest tenth.
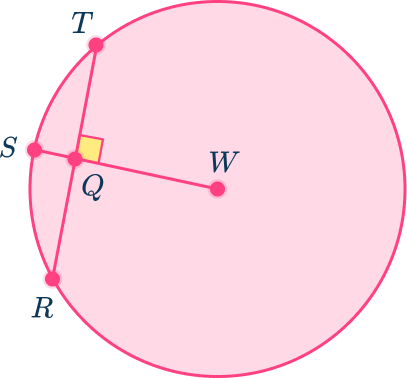
1.8 units

6.2 units

5 units

2 units

In circle W, the radius SW is perpendicular to chord RT so it also bisects chord RT, giving QR=QT.
Since RT=10, QT=RT=5.
Draw in another radius to create a right triangle in order to use the Pythagorean theorem.
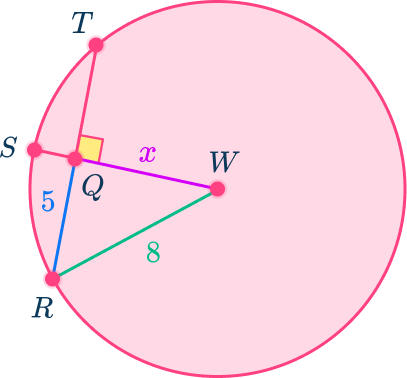
Since the radius SW=8, all the radii in the circle equal 8. Triangle WQR is a right triangle where the radius WR is the hypotenuse.
5^2+x^2=8^2
25+x^2=64
\begin{aligned} x^{2}&=39\\\\ x&=\sqrt{39}\approx{6.2} \end{aligned}
So QW=6.2
In order to find QS, take the radius SW and subtract QW from it.
QS=SW-QW=8-6.2=1.8
6. A semicircle entryway is being built in the King’s new home. They want to hang a light from the middle of the semicircle which is represented by point K to the point H.
The width of the entryway is 8.5 feet and the distance from point L to point M of the entryway is 5 feet. What is the maximum height of the hanging light HK? Round your answer to the nearest tenth.
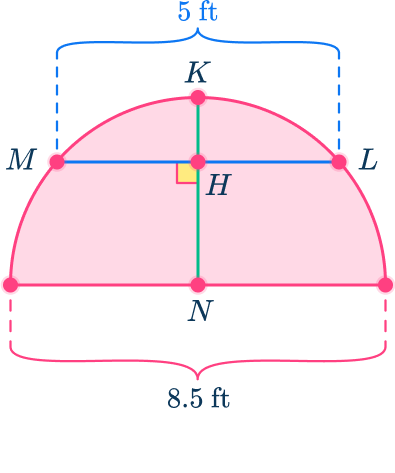




The center of the semicircle is point N.
The diameter of the semicircle is 8.5 feet so the radius is 4.25{~ft}.
The radius is the perpendicular bisector of the chord LM so HL=HM=2.5{~ft}.
Sketching another radius to create a right triangle MHN where point M is on the circumference of a circle.
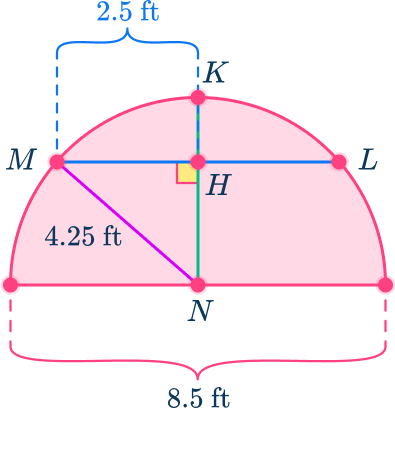
\begin{aligned} 4.25^2&=x^2+2.5^2 \\\\ 18.0625&=x^2+6.25 \\\\ 18.0625-6.25&=x^2 \\\\ x^2&=11.8125 \\\\ x&=\sqrt{11.8125}\approx{3.44} \end{aligned}
The distance from the bottom of the light to the ground is 3.44 feet so the maximum height of the light HK=4.25-3.44=0.81{~ft}.
Circle chord theorems FAQs
Yes, there are times where you might need to use trigonometry to find missing angles or chord lengths when applying circle chord theorems.
A secant line is a line that intersects a curve or circle at two points.
A cyclic quadrilateral is a quadrilateral that is inscribed in a circle meaning it is contained inside a circle with all 4 vertices on the circumference of the circle (edge of the circle).
The alternate segment theorem, is also known as the tangent-chord theorem. It is one of the circle theorems which states that the angle between a chord and a tangent through one of the chord’s endpoints is equal to the angle in the alternate segment of the chord.
The theorem is used to find missing angle and arc measurements. According to the alternate segment theorem, angle ABC is equal to angle EAC and angle BCA is equal to angle BAD. 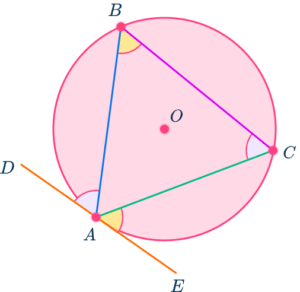
The next lessons are
- Types of data
- Averages and range
- Representing data
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!