High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Types of triangles Isosceles triangles Area of a triangle Parts of a circle Area of a circle Circumference of a circle Central angle Interior and exterior angles of polygons Substitution Rearranging equations

Math resources Geometry

Angles of a circle

Area of a seg. of a circle

Area of a segment of a circle

Here you will learn about the area of a segment of a circle including how to identify a segment of a circle and how to find the area of it.

Students will first learn about the area of a segment of a circle as part of geometry in high school.

What is the area of a segment of a circle?

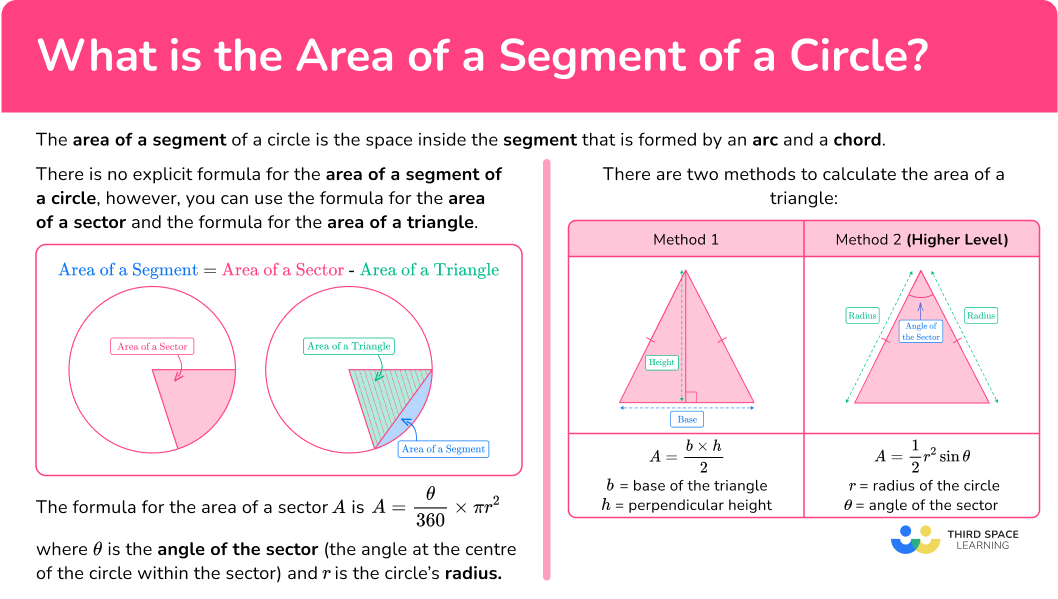
The area of a segment of a circle is the space inside the segment that is formed by an arc and a chord.

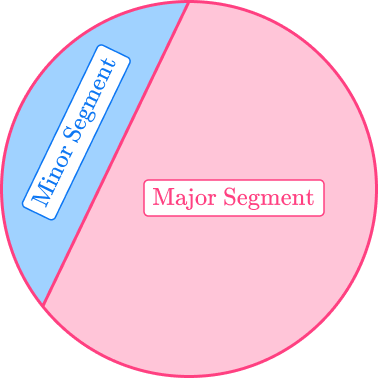
There are two types of segments,

A minor segment is a segment where the arc length is less than half of the circumference of the circle.

A major segment is a segment where the arc length is greater than half of the circumference of the circle.

To find the area of a segment of a circle, you can use the formula for the area of a triangle and the formula for the area of a sector. You subtract the area of the triangle from the area of the sector.

Area of a Segment $=$ Area of a Sector – Area of a Triangle

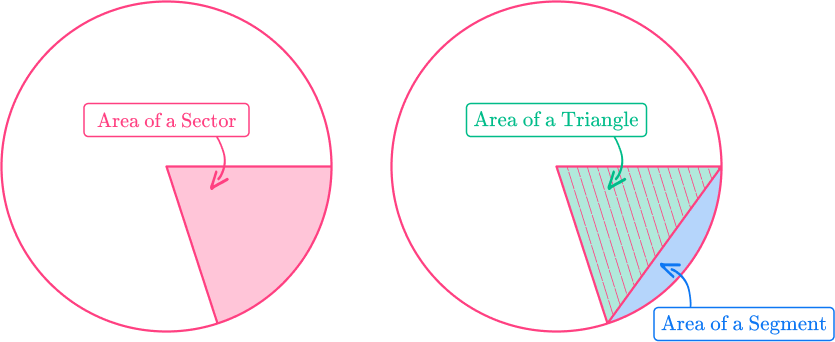
The formula for the area of a sector is

$\text{Area of a sector}=\cfrac{\theta}{360}\times\pi{r^2}$

where $\theta$ is the angle of the sector (the angle at the center of the circle within the sector) and $r$ is the radius of the circle.

Step-by-step guide: Area of a sector

[FREE] Area Worksheet (Grade 4 to 6)

Use this quiz to check your grade 4 to 6 students’ understanding of area. 15+ questions with answers covering a range of 4th, 6th and 7th grade area topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Area Worksheet (Grade 4 to 6)

DOWNLOAD FREE

There are two methods to calculate the area of a triangle. For both methods, notice that the triangle formed within a sector is always isosceles (two equal sides and two equal angles at the circumference of the circle).

Method 1: $\text{Area of a triangle}=\cfrac{\text{base}\times\text{perpendicular height}}{2}$

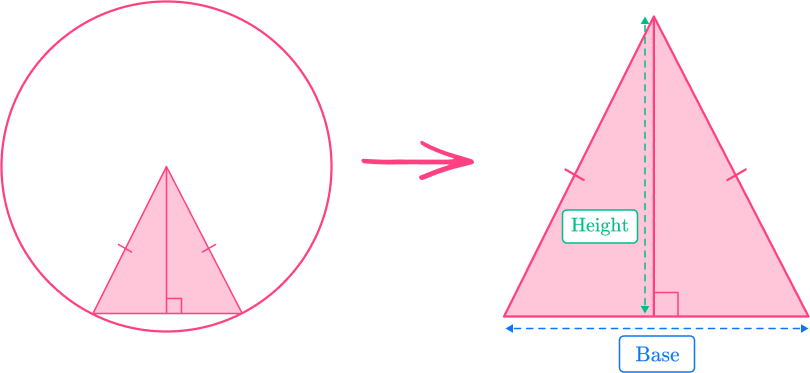
This method can be used if you know:

The distance from the chord to the center of the circle (which is equal to the perpendicular height of the triangle). This is NOT the radius of the circle.
The length of the chord (which is equal to the base of the triangle).

You can use Pythagoras’ Theorem if you know the radius to determine either of these values.

See also: Pythagoras’ Theorem

Method 2: $\text{Area of a triangle}=\cfrac{1}{2} \, ab\sin{C}$

Higher level – There is also a trigonometric formula you can use to find the area of a triangle. This is useful for triangles where you don’t know the height and you are unable to calculate it.

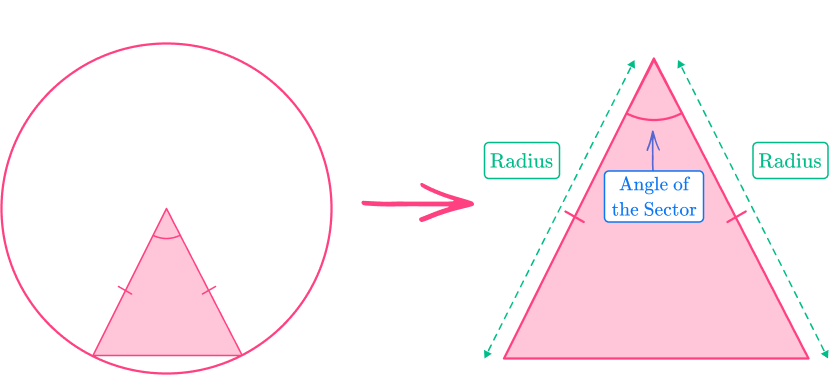
This method can be used if you know:

The radius of the circle (half the diameter).
The angle at the center of the circle within the sector. Remember that angles in a triangle sum to $180^{\circ}$ and the triangle is isosceles, so the two angles at the circumference of the circle are equal.

See also: $\cfrac{1}{2} \, ab\sin{C}$

As the lengths $a$ and $b$ are equal to the radius $r$ of the circle and $C$ is the included angle $\theta,$ you can adapt the formula for the area of a triangle to be:

$A=\cfrac{1}{2} \, r^{2}\sin{\theta}$

This method can be used for any triangle. It is useful to always calculate the area of the minor sector and subtract from the area of a circle if the segment is greater than half the area of the circle.

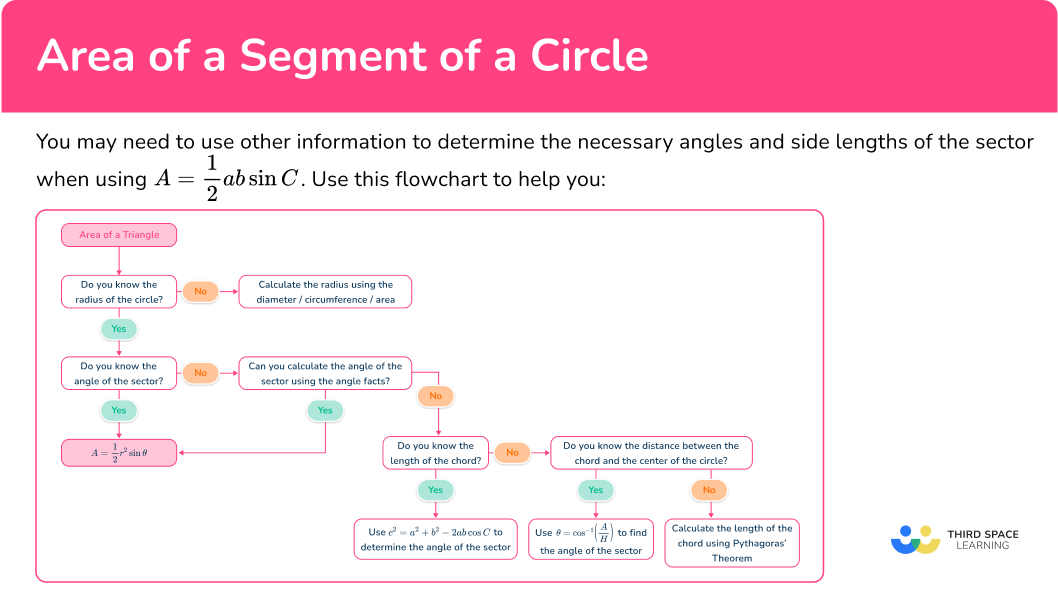
You may need to use other information to determine the necessary angles and side lengths of the sector when using $A=\cfrac{1}{2} \, r^{2}\sin{\theta}.$ Use this flowchart to help you:

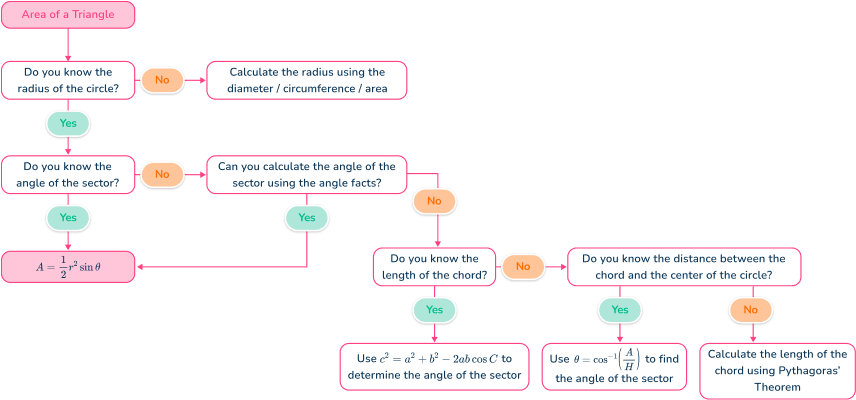
What is the area of a segment of a circle?

Common Core State Standards

How does this relate to high school math?

High School – Geometry – Circles (HS.G.C.B.5)
Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector.

How to calculate the area of a segment of a circle

In order to calculate the area of a segment:

Find the length of the radius.
Find the size of the angle creating the sector.
Find the area of the sector.
Find the area of the triangle created by the radii and the chord of a circle.
Subtract the area of the triangle from the area of the sector.
Clearly state your answer.

Area of a segment of a circle examples

Example 1: area of a minor segment using area of a triangle formula

Calculate the shaded region. Give your answer correct to the nearest hundredth ( $2$ decimal places).

Find the length of the radius.

Radius $=3\mathrm{~cm}$

2Find the size of the angle creating the sector.

\theta=90^{\circ}

3Find the area of the sector.

The sector area is:

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{90}{360}\times\pi\times{3^2} \\\\ &=\cfrac{9}{4} \, \pi\mathrm{~cm}^2 \end{aligned}

Note – You could have found the area of the sector, in this instance, by using the area of a circle formula to find the area of the circle as a whole, and then divided by four, because this sector has a $90^{\circ}$ angle, which means it is one-quarter of the whole circle.

4Find the area of the triangle created by the radii and the chord of a circle.

The triangle created by the radii and the chord of the circle is the white section of the sector. It is a right triangle.

The area of the triangle is:

\begin{aligned}A&=\cfrac{b\times{h}}{2} \\\\ &=\cfrac{3\times{3}}{2} \\\\ &=4.5\mathrm{~cm}^2 \end{aligned}

5Subtract the area of the triangle from the area of the sector.

The area of the shaded region, which is the segment, is

=\cfrac{9}{4} \, \pi-4.5=2.5685…

6Clearly state your answer.

The question asks for the answer to the nearest hundredth, so you write the answer as $2.57\mathrm{~cm}^2$ .

Example 2: area of a major segment using area of a triangle formula

Calculate the area of the major segment. Give your answer to the nearest hundredth.

Find the length of the radius.

Radius $=5\mathrm{~cm}$

Find the size of the angle creating the sector.

As you are finding the area of the major sector, subtract the area of the minor sector from the area of the full circle. This means that the angle for the minor sector is $\theta=90^{\circ}$ .

Find the area of the sector.

The area of the minor sector is:

$\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{90}{360}\times\pi\times{5^2} \\\\ &=\cfrac{25}{4} \, \pi\mathrm{~cm}^2 \end{aligned}$

Note – Keep the answer in terms of $\pi$ to maintain the best level of accuracy.

Find the area of the triangle created by the radii and the chord of a circle.

The area of the triangle for the minor sector is:

$\begin{aligned}A&=\cfrac{b\times{h}}{2} \\\\ &=\cfrac{5\times{5}}{2} \\\\ &=12.5\mathrm{~cm}^2 \end{aligned}$

Subtract the area of the triangle from the area of the sector.

The area of the minor segment, is

$\cfrac{25}{4} \, \pi-12.5=7.134954085…$

The question asks for the area of the major segment so the area of the minor segment needs to be subtracted from the area of the circle.

The area of a circle is $A=\pi{r^2}.$ As $r=5,$

$A=\pi\times{5^{2}}=25\pi\mathrm{~cm}^{2}.$

Subtract the area of the minor segment from the circle

$25\pi-7.134954085…=71.40486225…$

Clearly state your answer.

The question states that the answer should be rounded to the nearest hundredth.

Area of the major segment $=7.13\mathrm{~cm}^2$

Example 3: using trigonometry

Calculate the shaded region. Give your answer to $3$ significant figures.

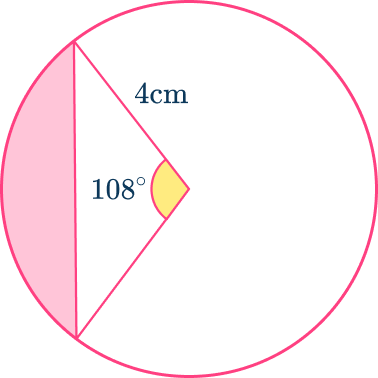
Find the length of the radius.

Radius $=4\mathrm{~cm}$

Find the size of the angle creating the sector.

\theta=108^{\circ}

Find the area of the sector.

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{108}{360}\times\pi\times{4^2} \\\\ &=\cfrac{24}{5} \, \pi\mathrm{~cm}^2 \end{aligned}

Note – Do not round your answer at this stage, for accuracy.

Find the area of the triangle created by the radii and the chord of a circle.

You know the radius of the circle and the angle of the sector, so you use trigonometry for the area of a triangle.

$A=\cfrac{1}{2} \, r^{2}\sin\theta$

where $r$ is the radius, and $\theta$ is the angle of the sector.

The area of the triangle is:

$\begin{aligned}A&=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{4}^{2}\times\sin(108) \\\\ &=7.60845213…\mathrm{~cm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Subtract the area of the triangle from the area of the sector.

The area of the shaded region, which is the segment, is

$\cfrac{24}{5} \, \pi-7.60845213…=7.47119261…$

Clearly state your answer.

The question asks for the answer rounded to $3$ significant figures, so you can round it and give the answer as $7.47\mathrm{~cm}^2.$

Example 4: theta not given

The radius of a circle is $6\mathrm{~mm}.$ Calculate the area of the shaded segment. Give your answer to $3$ significant figures.

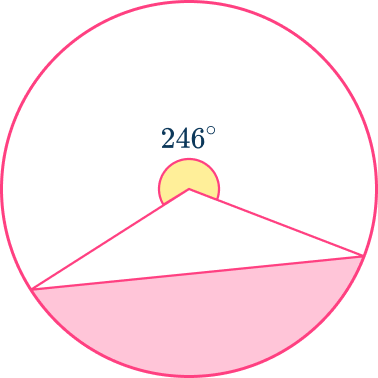
Find the length of the radius.

The length of the radius is given in the question.

Raduis $=6\mathrm{~mm}$

Find the size of the angle creating the sector.

The angle creating the sector is not marked on the diagram. However, you can use the angle fact ‘angles around a point add to $360^{\circ}$ ’ to calculate the angle creating the sector.

$\theta=360-246=114^{\circ}$

Find the area of the sector.

The area of the sector is:

$\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{114}{360}\times\pi\times{6^2} \\\\ &=\cfrac{57}{5} \, \pi\mathrm{~mm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Find the area of the triangle created by the radii and the chord of a circle.

You do not know the height of the triangle created by the radii and the chord of the circle in this example. So, you use the trigonometric formula for the area of a triangle:

$A=\cfrac{1}{2} \, r^{2}\sin\theta$

where $r$ is the radius, and $\theta$ is the angle of the sector.

The area of the triangle is:

$\begin{aligned}A&=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{6^2}\times\sin(114) \\\\ &=16.44381824…\mathrm{~mm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Subtract the area of the triangle from the area of the sector.

The area of the shaded region, which is the segment, is

$\cfrac{57}{5} \, \pi-16.44381824…=19.37074426…$

Clearly state your answer.

The question asks for the answer rounded to $3$ significant figures, so you can round it and give the answer as $19.4\mathrm{~mm}^2.$

Example 5: given base angle of isosceles triangle

Below is a circle with radius $4\mathrm{~mm}.$ Calculate the area of the shaded segment. Give your answer to $3$ significant figures.

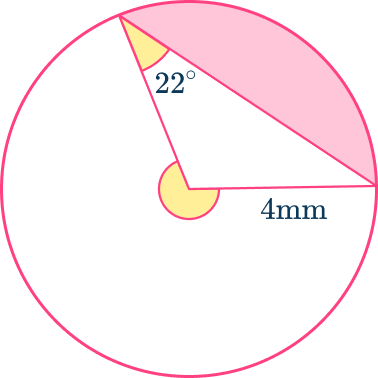
Find the length of the radius.

The length of the radius is given in the question.

Radius $=4\mathrm{~mm}$

Find the size of the angle creating the sector.

The angle creating the sector is not marked on the diagram. You need to calculate it. The first thing to recognize is which sides of the triangle formed in the sector are radii and which is the chord.

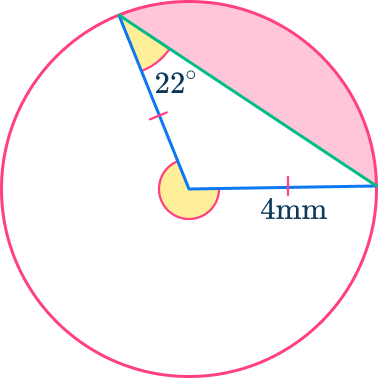
The two sides that meet in the center of the circle are both radii and are, therefore, equal in length. The third side of the triangle cuts the circle from circumference to circumference, not passing through the center, so is the chord.

The fact that you have two equal sides in this triangle, means it is isosceles.

The angle facts ‘base angles in an isosceles triangle are equal’ and ‘angles in a triangle add to $180^{\circ}$ ’ will help us to calculate the angle creating the sector, $\theta.$

$\theta=180-(22+22)=136^{\circ}$

Find the area of the sector.

The area of the sector is:

$\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{136}{360}\times\pi\times{4^2} \\\\ &=\cfrac{272}{45} \, \pi\mathrm{~mm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Find the area of the triangle created by the radii and the chord of a circle.

You do not know the height of the triangle created by the radii and the chord of the circle in this example. So, you use the area formula

$A=\cfrac{1}{2} \, r^{2}\sin\theta$

where $r$ is the radius, and $\theta$ is the angle of the sector.

The area of the triangle is:

$\begin{aligned}A&=\cfrac{1}{2} \, r^{3}\sin\theta \\\\ &=\cfrac{1}{2}\times4^{2}\times\sin(136) \\\\ &=5.557266964…\mathrm{~mm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Subtract the area of the triangle from the area of the sector.

The area of the shaded region, which is the segment, is

$\cfrac{272}{45} \, \pi-5.557266964…=13.4319153…$

Clearly state your answer.

The question asks for the answer rounded to $3$ significant figures, so you can round it and give the answer as $13.4\mathrm{~mm}^2.$

Example 6: missing radius

Below is a sector. The area of the sector is $67.02\mathrm{~cm}^2.$ The radius of the sector, $r,$ is an integer.

Calculate the area of the segment labeled $B.$ Give your answer to $3$ significant figures.

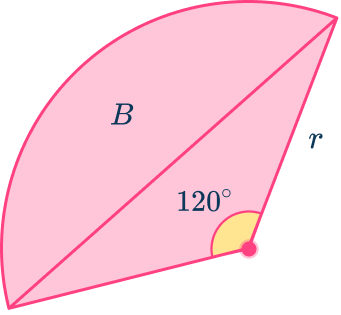
Find the length of the radius.

The length of the radius is given in the question as $r.$ So you need to calculate it.

You are given the area of the sector, so you can use this to calculate the radius.

Substituting what you know into the formula for the area of a sector you get $67.02=\cfrac{120}{360}\times\pi\times{r^2}.$

Rearranging this to make $r^2$ the subject gives

$r^2=\cfrac{67.02}{\cfrac{120}{360}\times\pi}$

So $r^2=63.99938572\dots$

You want the radius, $r,$ so you need to square root $r^2,$ to give

$r=7.999961607\dots$

The question tells us that the radius, $r,$ is an integer, so for this example you can say, $r=8\mathrm{~cm}.$

Find the size of the angle creating the sector.

\theta=120^{\circ}

Find the area of the sector.

The area of the sector is given in the question as $67.02\mathrm{~cm}^2.$

Find the area of the triangle created by the radii and the chord of a circle.

You do not know the height of the triangle created by the radii and the chord of the circle in this example. So, you use the trigonometric formula for the area of a triangle,

$A=\cfrac{1}{2} \, r^{2}\sin\theta$

where $r$ is the radius, and the angle $\theta$ is the angle creating the sector.

The area of the triangle is:

$\begin{aligned}A&=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times8^{2}\times\sin(120) \\\\ &=27.71281292…\mathrm{~cm}^2 \end{aligned}$

Note – Do not round your answer at this stage, for accuracy.

Subtract the area of the triangle from the area of the sector.

The area of the segment is

$67.02 - 27.71281292\dots= 39.30718708\dots$

Clearly state your answer.

The question asks for the answer rounded to $3$ significant figures, so you can round it and give the answer as $39.3\mathrm{~cm}^2.$

Teaching tips for area of a segment of a circle

Provide examples where the chord is a diameter and the area is half the circle (a semicircle), then transition to problems with shorter chords. This helps students understand how the segment’s area changes relative to the chord’s length.

Explain how inscribed angles can help simplify calculations for certain segments. Remind students that an inscribed angle is half the measure of the central angle that subtends the same arc. This can be useful when the problem involves inscribed angles instead of central angles, as it allows them to find the corresponding central angle easily for area calculations.

Easy mistakes to make

Confusing sector and segment
Sometimes the two can be confused. Remember,

A sector is formed when a circle is divided using two radii.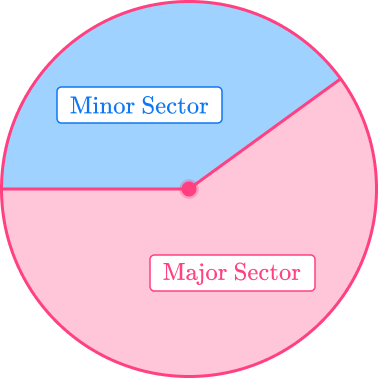

A segment is the area enclosed by an arc of a circle and a chord.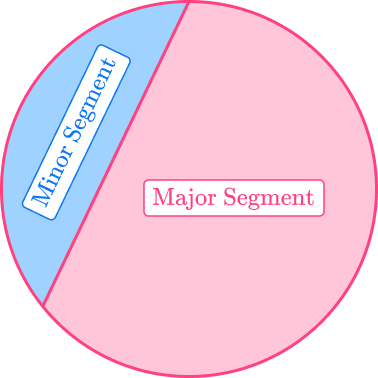

Not recognizing the angle creating the sector
The angle $C$ is the angle inside the sector you’re working with.

For example, in the diagram below, it is the angle $112^{\circ}$ that creates the sector, not the angle labeled $248^{\circ}.$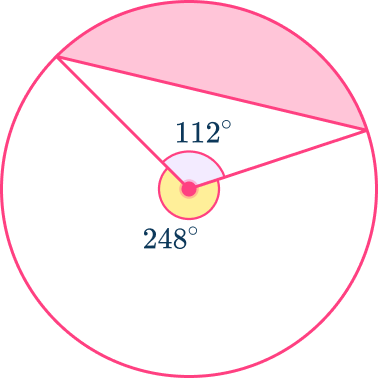

Note that the area of the segment is the shaded region.

Rounding too early
It is important to not round your answers in your work until you get to the end where you can round your final answer as the question asks. Otherwise, you could make your final answer slightly inaccurate.

Angles of a circle
Segment of a circle
Arc of a circle
Arc length formula
Perimeter of a sector

Practice area of a segment questions

14\mathrm{~cm}^2

13.98\mathrm{~cm}^2

62.98\mathrm{~cm}^2

63\mathrm{~cm}^2

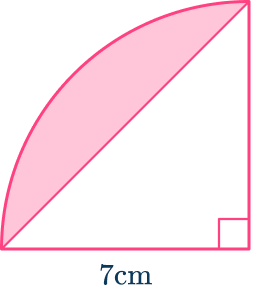
You need to calculate the area of the sector and the area of the triangle, then subtract the area of the triangle from the area of the sector.

The area of the sector is

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{90}{360}\times\pi\times{7^2} \\\\ &=\cfrac{49}{4} \, \pi\mathrm{~cm}^2 \end{aligned}

The area of the triangle is

A=\cfrac{b\times{h}}{2}=\cfrac{7\times{7}}{2}=24.5\mathrm{~cm}^2

Hence, the area of the segment is

$\cfrac{49}{4} \, \pi-24.5=13.98\mathrm{~cm}^2$ (nearest hundredth)

7.43\mathrm{~mm}^2

7.57\mathrm{~mm}^2

11.57\mathrm{~mm}^2

11.43\mathrm{~mm}^2

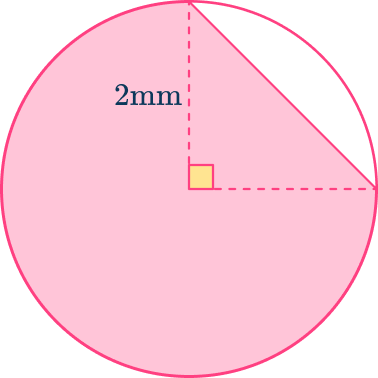
You need to calculate the area of the minor sector and the area of the triangle, then subtract the area of the triangle from the area of the sector. Finally, subtract the area of the minor segment from the area of the circle to find the area of the major sector.

The area of the sector is

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{90}{360}\times\pi\times{2^2} \\\\ &=\pi\mathrm{~mm}^2 \end{aligned}

The area of the triangle is

A=\cfrac{b\times{h}}{2}=\cfrac{2\times{2}}{2}=2\mathrm{~mm}^2

Hence, the area of the minor segment is

$\pi-2=1.14\mathrm{~mm}^{2}$ (nearest hundredth)

The area of the circle is

A=\pi\times{2^2}=4\pi\mathrm{~mm}^{2}

Hence, the area of the major segment is

$4\pi-1.14=11.43\mathrm{~mm}^{2}$ (nearest hundredth)

77.98\mathrm{~mm}^2

179.77\mathrm{~mm}^2

178\mathrm{~mm}^2

78\mathrm{~mm}^2

You need to calculate the area of the sector and the area of the triangle, then subtract the area of the triangle from the area of the sector.

First you need to calculate $\theta,$ the angle that creates the sector.

The two sides that meet in the center of the circle are both radii, therefore, equal in length. The third side of the triangle cuts the circle from circumference to circumference, not passing through the center, so is the chord.

The fact that you have two equal sides in this triangle, means it is isosceles.

The angle facts ‘base angles in an isosceles triangle are equal’ and ‘angles in a triangle add to $180^{\circ}$ ’ will help us to calculate the angle creating the sector, $\theta.$

\theta=180-18-18=144^{\circ}

The area of the sector is

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{144}{360}\times\pi\times{9^2} \\\\ &=\cfrac{162}{5} \, \pi\mathrm{~mm}^2 \end{aligned}

The area of the triangle is

\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{9^2}\times\sin(144) \\\\ &=23.80530272… \mathrm{~mm}^2 \end{aligned}

Hence, the area of the segment is

$\cfrac{162}{5} \, \pi-23.80530272…=77.98\mathrm{~mm}^2$ (nearest hundredth)

17\mathrm{~cm}^2

7.02\mathrm{~cm}^2

17.39\mathrm{~cm}^2

7\mathrm{~cm}^2

You need to calculate the area of the sector and the area of the triangle. Then subtract the area of the triangle from the area of the sector.

First you need to calculate $\theta,$ the angle that creates the sector.

You can use the angle fact ‘angles around a point add to $360^{\circ}$ ’ to calculate the angle creating the sector.

\theta=360-228=132^{\circ}

The area of the sector is

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{132}{360}\times\pi\times{3^2} \\\\ &=\cfrac{33}{10} \, \pi\mathrm{~cm}^2 \end{aligned}

The area of the triangle is

\begin{aligned}A& =\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{3^2}\times\sin(132) \\\\ &=3.344151715…\mathrm{~cm}^2 \end{aligned}

Hence, the area of the segment is

$\cfrac{33}{10} \, \pi-3.344151715…=7.02\mathrm{~cm}^2$ (nearest hundredth)

43.74\mathrm{~cm}^2

44\mathrm{~cm}^2

17\mathrm{~cm}^2

16.69\mathrm{~cm}^2

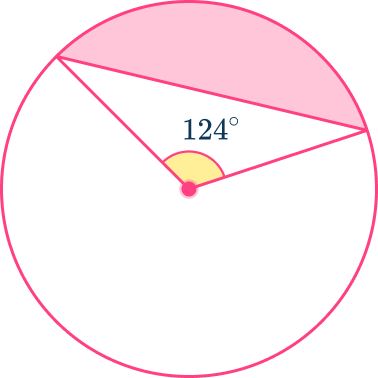
You need to calculate the area of the sector and the area of the triangle. Then subtract the area of the triangle from the area of the sector.

The area of the sector is

\begin{aligned}A&=\cfrac{\theta}{360}\times\pi{r^2} \\\\ &=\cfrac{124}{360}\times\pi\times{5^2} \\\\ &=\cfrac{155}{18} \, \pi\mathrm{~cm}^2 \end{aligned}

The area of the triangle is

\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{5^2}\sin(124) \\\\ &=10.36296966…\mathrm{~cm}^2 \end{aligned}

Hence, the area of the segment is

$\cfrac{155}{18} \, \pi-10.36296966…=16.69\mathrm{~cm}^2$ (nearest hundredth)

16.81\mathrm{~cm}^2

51.05\mathrm{~cm}^2

51\mathrm{~cm}^2

17\mathrm{~cm}^2

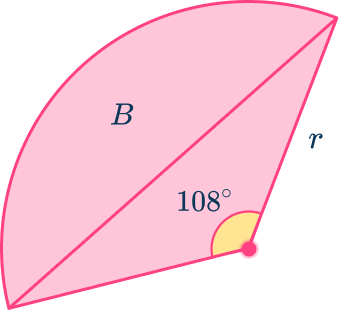
You need to calculate the area of the sector and the area of the triangle. Then subtract the area of the triangle from the area of the sector.

The length of the radius is given in the question as $r.$ So you need to calculate it. You are given the area of the sector, so you can use this to calculate the radius.

Substituting what you know into the formula for the area of a sector you get

33.93=\cfrac{108}{360}\times\pi\times{r^2}.

Rearranging this to make $r^2$ the subject gives

r^2=\cfrac{33.93}{\cfrac{108}{360}\times\pi}.

So, $r^2=36.00084813\dots$

You want the radius, $r,$ so you need to square root $r^2,$ to give

r=6.000070677\dots

The question tells us that the radius, $r,$ is an integer, so you can say, $r=6\mathrm{~cm}.$

The area of the sector is given in the question. So you need to find the area of the triangle.

The area of the triangle is

\begin{aligned}A&=\cfrac{1}{2} \, ab\sin{C} \\\\ &=\cfrac{1}{2} \, r^{2}\sin\theta \\\\ &=\cfrac{1}{2}\times{6^2}\times\sin(108) \\\\ &=17.11901729\mathrm{~cm}^2 \end{aligned}

Hence, the area of the segment is

$33.93-17.11901729…=16.81\mathrm{~cm}^2$ (nearest hundredth)

Area of a segment of a circle FAQs

How do you find the area of a segment of a circle?

Since there is no formula for the area of a segment of a circle, you can use the formula for the area of a triangle and the formula for the area of a sector. First determine the area of the sector, then subtract the area of the triangle formed by the radii and the chord to get the area of the segment.

What is the difference between a segment of a circle and a sector of a circle?

A segment of a circle is the area between a chord and the corresponding arc. A sector of a circle is the area between two radii and the corresponding arc.

What is the difference between the area of a segment of a circle and the surface area?

The area of a segment of a circle is the part of the circle’s area cut off by a chord. The surface area generally refers to a segment of a sphere and involves the curved surface area of that spherical segment.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.