High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Coordinate plane Plot points on a graph Linear graph

Math resources Algebra Graphing linear equations

Slope intercept form

y = mx + b

Here you will learn about the slope-intercept form of a line, $y=m x+b,$ including how to recognize the slope and $y$ -intercept from the equation $y=m x+b$ and rearrange an equation into slope intercept form $y=m x+b.$

Students first work with linear equations in $7$ th grade when they learn about the constant of proportionality and direct variation. They expand their knowledge as they move through $8$ th grade and high school math.

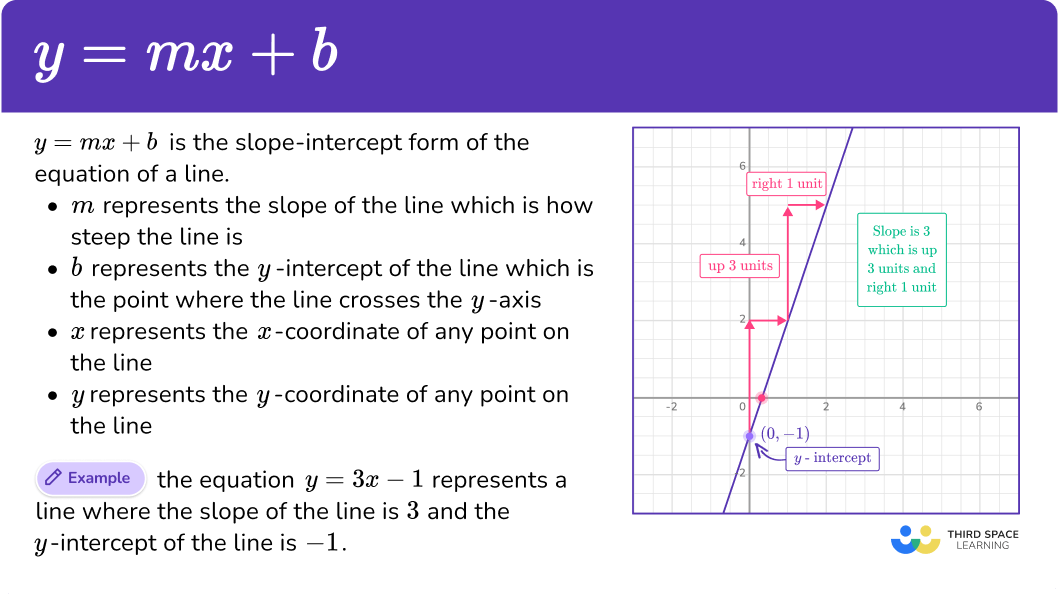
What is y = mx + b?

$y=m x+b$ is the slope intercept form of the line. There are other ways to write the equation of a straight line like standard form or point slope form. However, the focus here is going to be on the slope-intercept form of the equation of a line, $y=m x+b.$

$m$ represents the slope of a line which is how steep the line is
$b$ represents the $y$ -intercept of the line which is the point where the line intersects the $y$ -axis
$x$ value represents the $x$ -coordinate of any point on the line
$y$ value represents the $y$ -coordinate of any point on the line

$y=m x+b$ is a linear equation because when it’s graphed on the coordinate plane, it forms a line. You can also determine this because the power of $x$ is equal to $1.$

Let’s take a look at the linear equation $y=2 x+1.$

Since $m$ is represented by the number $2$ and $b$ is represented by the number $1.$ You can state that the slope of this line is $2$ and the $y$ -intercept is $1.$

Graphically, you can see that the ordered pair of the $y$ -intercept is $(0, 1)$ and the slope is represented by $2$ units up and $1$ unit to the right.

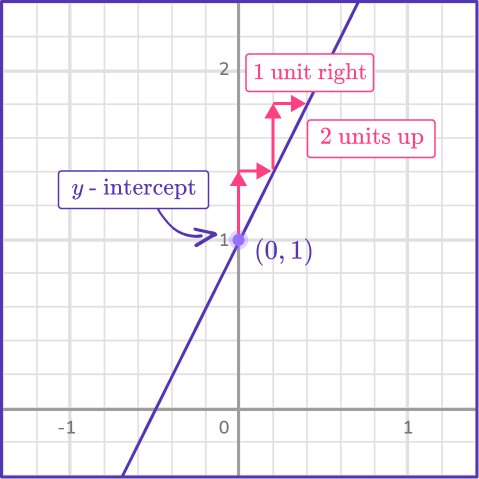
Since the $x$ and $y$ represent the coordinates of any point on the line, you can create a table of values to find ordered pairs to represent the line graphically. Recall that the independent variable is $x$ and the dependent variable is $y.$

[FREE] Algebra Worksheet (Grade 6 to 8)

Teaching slope-intercept form of a line? Use this quiz to check your grades 6–8 students’ understanding of algebra. 10+ questions with answers covering a range of topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Worksheet (Grade 6 to 8)

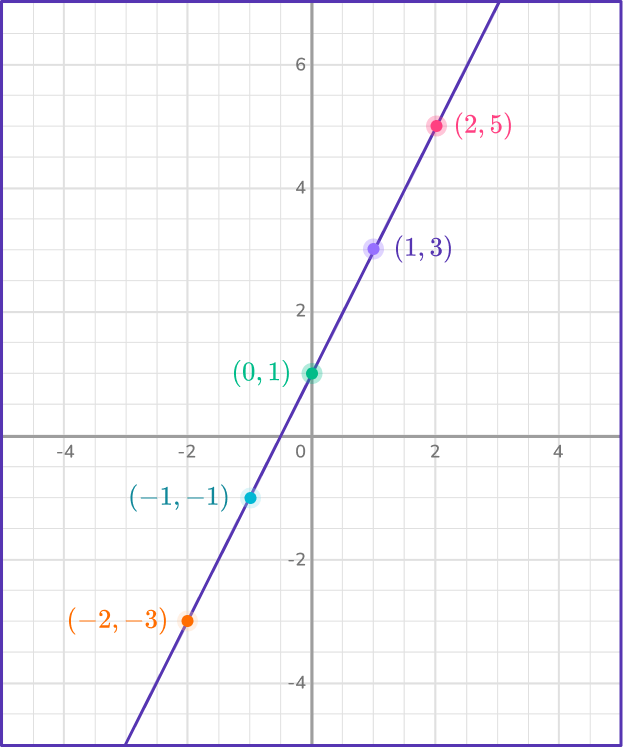
DOWNLOAD FREE

Here is a quick summary of some equations in the form $y=m x+b$ with the slope and $y$ intercept highlighted.

Special cases:

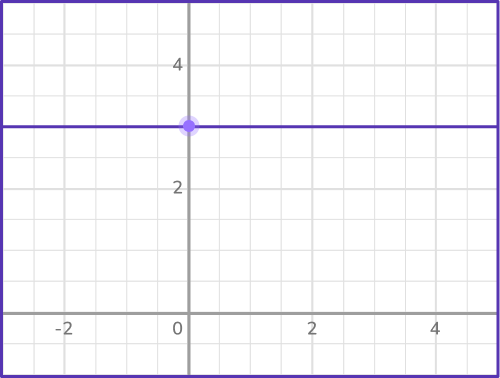
Horizontal lines

Horizontal lines have a slope of $0.$

So, the equation in slope-intercept form of the horizontal line below can be expressed as, $y=0 x+3$ which can be written as $y=3.$

Vertical lines:

Vertical lines have an undefined slope.

So, the equation of the line graphed below can be expressed as $x=3.$ The equation of all vertical lines will be the $x$ value of where the line intersects the $x$ axis.

What is y = mx + b?

Common Core State Standards

How does this relate to $8$ th grade math and high school math?

Grade 8 Functions (8.F.A.3)
Interpret the equation $y=m x+b$ as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function $A=s^2$ giving the area of a square as a function of its side length is not linear because its graph contains the points $(1,1), (2, 4)$ and $(3,9),$ which are not on a straight line.

Grade 8 Expressions and Equations (8.EE.B.6)
Use similar triangles to explain why the slope $m$ is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation $y = m x$ for a line through the origin and the equation $y = m x + b$ for a line intercepting the vertical axis at $b.$

High School Functions: Interpreting Functions (HSF-IF.C.7a)
Graph linear and quadratic functions and show intercepts, maxima, and minima.

High School Functions: Linear, Quadratic, and Exponential Models (HSF-LE.A.2)
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).

How to use y = mx + b

In order to state the slope and y-intercept of a line:

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$
Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$
State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

y = mx + b examples

Example 1: y = mx + b form

State the slope and $y$ -intercept of the line $y=-3 x+8.$

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The equation $y=-3 x+8$ is already in slope intercept form, $y=m x+b,$ so you can progress to step $2.$

2Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the given equation of $y=-3 x+8$ to the slope intercept form of a linear equation, $y=m x+b.$

You can conclude that:

$m=-3$ because it is the coefficient of the $x$ term

$b=8$ because it is the constant

3State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope is $-3$ which is the same as $-\cfrac{3}{1},$ the slope of this line is $3$ units down and $1$ unit to the right OR $3$ units up and $1$ unit left.

The $y$ -intercept is $8$ which means the line crosses the $y$ -axis at $8$ so the coordinate of the $y$ -intercept is $(0, 8).$ You can also find this by plugging in a $0$ for $x$ and solving for $y.$

\begin{aligned}&y=-3 x+8 \\\\ &\begin{aligned}& y=-3(0)+8 \\\\ & y=0+8 \\\\ & y=8 \end{aligned}\end{aligned}

Example 2: y = b + mx form

Find the slope and $y$ -intercept of the line $y=7-x.$

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The given equation is not in the form of $y=m x+b.$

By rearranging the terms, you can write it in the correct form.

$y=7-x$

$y=-x+7$ (simply rearrange the right handside of the equation writing the $x$ term first and then the constant term.)

Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the rearranged equation of $y=-x+7$ to the slope intercept form of a linear equation, $y=m x+b$

You can conclude that:

$m=-1$ because it is the coefficient of the $x$ term

$b=7$ because it is the constant term

State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope is $-1$ which is the same as $-\cfrac{1}{1},$ the slope of this line is $1$ unit down and $1$ unit to the right OR $1$ unit up and $1$ unit left.

The $y$ -intercept is $7$ which means the line crosses the $y$ -axis at $7$ so the coordinate of the $y$ -intercept is $(0, 7).$ You can also find this by plugging in a $0$ for $x$ and solving for $y.$

$\begin{aligned}&\begin{aligned}& y=-x+7 \\\\ & y=-1(0)+7 \\\\ & y=0+7\end{aligned}\\\\ &y=7\end{aligned}$

Example 3: solve the equation for y

Find the slope and $y$ -intercept of the line $x=y+10.$

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The given equation is not in the slope intercept form equation, $y=m x+b.$ So, you need to solve the equation, $x=y+10,$ for $y.$

$\begin{aligned}& x=y+10 \\\\ & x-y=y-y+10 \\\\ & x-y=10 \\\\ & x-x-y=10 \\\\ & -y=-x+10 \\\\ & \cfrac{-y}{-1}=\cfrac{-x}{-1}+\cfrac{10}{-1} \\\\ & y=x-10\end{aligned}$

Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the rearranged equation of $y=x-10$ to the slope intercept form of a linear equation, $y=m x+b$

You can conclude that:

$m=1$ because it is the coefficient of the $x$ term

$b=-10$ because it is the constant term

State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope is $1$ which is the same as $\cfrac{1}{1},$ the slope of this line is $1$ unit down and $1$ unit to the right.

The $y$ -intercept is $-10$ which means the line crosses the $y$ -axis at $-10$ so the coordinate of the $y$ -intercept is $(0, -10).$ You can also find this by plugging in a $0$ for $x$ and solving for $y.$

$\begin{aligned}& y=x-10 \\\\ & y=1(0)-10 \\\\ & y=0-10 \\\\ & y=-10\end{aligned}$

Example 4: solve the equation for y with a fraction

Find the slope and $y$ -intercept of the line $2 x=6 y-15.$

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The given equation is not in the form of $y=m x+b.$ So, you need to solve the equation, $2 x=6 y-15,$ for $y.$

$\begin{aligned}&\begin{aligned}& 2 x=6 y-15 \\\\ & 2 x-6 y=6 y-6 y-15 \\\\ & 2 x-2 x-6 y=-2 x-15 \\\\ & -6 y=-2 x-15\end{aligned}\\\\ &\cfrac{-6 y}{-6}=\cfrac{-2 x}{-6}-\cfrac{15}{-6}\end{aligned}$

$y=\cfrac{1 x}{3}+\cfrac{15}{6} \;\,$ (simplify the fractions when necessary)

$y=\cfrac{1 x}{3}+\cfrac{5}{2}$

Remember that,

$\begin{aligned}& \cfrac{1 x}{3}=\cfrac{1}{3} x \\\\ & \cfrac{5}{2}=2 \cfrac{1}{2}\end{aligned}$

So you can write the equation as, $y=\cfrac{1}{3} x+2 \cfrac{1}{2}.$

Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the rearranged equation of $y=\cfrac{1}{3} x+2 \cfrac{1}{2}$ to the slope intercept form of a linear equation, $y=m x+b.$

You can conclude that:

$m=\cfrac{1}{3}$ because it is the coefficient of the $x$ term

$b=2 \cfrac{1}{2}$ because it is the constant term

State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope of this line is $\cfrac{1}{3},$ this means that the slope is $1$ unit up and $3$ units right.

The $y$ -intercept is $2 \cfrac{1}{2}$ which means the line crosses the $y$ -axis at $2 \cfrac{1}{2}$ so the coordinate of the $y$ -intercept is $(0, 2 \cfrac{1}{2} \, ).$

You can also find this by plugging in a $0$ for $x$ and solving for $y.$

$\begin{aligned}&y=\cfrac{1}{3}\, x+2 \cfrac{1}{2}\\\\ &\begin{aligned}& y=\cfrac{1}{3}\,(0)+2 \cfrac{1}{2} \\\\ &y=0+2 \cfrac{1}{2} \\\\ & y=2 \cfrac{1}{2}\end{aligned}\end{aligned}$

Example 5: solving for y with parentheses

Find the slope and $y$ -intercept of the line $3 x=4(y-5)$ .

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The given equation is not in the form of $y=m x+b.$ So, you need to solve the equation, $3 x=4(y-5),$ for $y.$

$\begin{aligned}&\begin{aligned}& 3 x=4(y-5) \\\\ & 3 x=4 y-20 \\\\ & 3 x-4 y=4 y-4 y-20 \\\\ & 3 x-3 x-4 y=-3 x-20 \\\\ & -4 y=-3 x-20\end{aligned}\\\\ &\cfrac{-4 y}{-4}=\cfrac{-3 x}{-4}-\cfrac{20}{-4}\end{aligned}$

$y=\cfrac{3 x}{4}+\cfrac{20}{4} \;\,$ (simplify the fractions when necessary)

$y=\cfrac{3 x}{4}+5$

Remember that,

$\cfrac{3 x}{4}=\cfrac{3}{4} x$

So you can write the equation as, $y=\cfrac{3}{4} x+5$

Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the rearranged equation of $y=\cfrac{3}{4} x+5$ to the slope intercept form of a linear equation, $y=m x+b.$

You can conclude that:

$m=\cfrac{3}{4}$ because it is the coefficient of the $x$ term

$b=5$ because it is the constant term

State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope of this line is $\cfrac{3}{4},$ this means that the slope is $3$ units up and $4$ units right.

The $y$ -intercept is $5$ which means the line crosses the $y$ -axis at $5$ so the coordinate of the $y$ -intercept is $(0, 5).$ You can also find this by plugging in a $0$ for $x$ and solving for $y.$

$\begin{aligned}& y=\cfrac{3}{4} x+5 \\\\ & y=\cfrac{3}{4}(0)+5 \\\\ & y=0+5\end{aligned}$

Example 6: solving for y with decimals

Find the slope and $y$ -intercept of the line $x=\cfrac{y+0.85}{0.2}.$

Rearrange the equation to make sure it is in the form of $\textbf{y = mx + b}.$

The given equation is not in the form of $y=m x+b.$ So, you need to solve the equation, $x=\cfrac{y+0.85}{0.2},$ for $y.$

$\begin{aligned}& x=\cfrac{y+0.85}{0.2} \\\\ & x \times 0.2=\cfrac{y+0.85}{0.2} \times 0.2 \\\\ & 0.2 x=y+0.85 \\\\ & 0.2 x-y=y-y+0.85 \\\\ & 0.2 x-0.2 x-y=-0.2 x+0.85 \\\\ & -y=-0.2 x+0.85 \\\\ & \cfrac{-y}{-1}=\cfrac{-0.2 x}{-1}+\cfrac{0.85}{-1} \\\\ & y=0.2 x-0.85\end{aligned}$

Remember that,

$\begin{aligned}& 0.2=\cfrac{2}{10}=\cfrac{1}{5} \\\\ & 0.85=\cfrac{85}{100}=\cfrac{17}{20}\end{aligned}$

So you can write the equation as, $y=0.2 x+0.85$ OR $y=\cfrac{1}{5} x+\cfrac{17}{20}.$

Identify the numbers that represent $\textbf{m}$ and $\textbf{b}.$

Comparing the rearranged equation of $y=0.2 x+0.85,$ which is the same as $y=\cfrac{1}{5} x+\cfrac{17}{20},$ to the slope intercept form of a linear equation, $y=m x+b.$

You can conclude that:

$m=0.2$ or $\cfrac{1}{5}$ because it is the coefficient of the $x$ term

$b=0.85$ or $\cfrac{17}{20}$ because it is the constant term

To interpret the slope, it is best to have a fraction.

State the slope as rise over run and the $\textbf{y}$ -intercept as an ordered pair.

Since the slope of this line is $\cfrac{1}{5},$ this means that the slope is $1$ unit up and $5$ units right.

The $y$ -intercept is $0.85$ or $\cfrac{17}{20}$ which means the line crosses the $y$ -axis at $0.85$ or $\cfrac{17}{20}$ so the coordinate of the $y$ -intercept is $(0, 0.85)$ or $(0, \cfrac{17}{20}\,).$

You can also find this by plugging in a $0$ for $x$ and solving for $y.$

$\begin{aligned}& y=0.2 x+0.85 \\\\ & y=0.2(0)+0.85 \\\\ & y=0+0.85 \\\\ & y=0.85\end{aligned}$

Teaching tips for y = mx + b

Use digital graphing platforms such as Desmos so that students can connect the algebraic equation to the visual representation of the graph.

Expose students using Desmos to special cases, such as when the $y$ -intercept is $0$ or when the slope is $0.$

When students are first learning the concept, encourage them to write the equation in correct slope intercept form where the $x$ term is first and then the constant.

Always provide creative opportunities for students such as having them create designs using linear equations on Desmos.

Instead of a worksheet, have students practice skills using digital platforms like Khan Academy.

Easy mistakes to make

Using the incorrect inverse operation
When rearranging equations, instead of applying the inverse operation to the term being moved, the value is simply moved to the other side of the equals sign.
For example,
$y+5=2 x$ is rearranged to make $y=2 x+5.$

Stating the value of $\textbf{m}$ and $\textbf{b}$ when the equation is not in the form $\textbf{y = mx + b}$
For example, in the equation, $x=y+10$ stating that the $m$ or slope is $1$ and that the $b$ or $y$ -intercept is $10.$ Instead of first rearranging the equation to be in slope intercept form.
$x=y+10$
$x-10=y+10-10$
$x-10=y$ which is the same as $y=x-10$

$m=1$ (slope)
$b=-10$ ( $y$ -intercept)

Mixing up the slope and the $\textbf{y}$ -intercept
For example, the equation $y=10+3 x.$ Since the equation is not quite in slope-intercept form, $y=m x+b,$ students might think that the slope is $10$ because it is written first and that the $y$ -intercept is $3.$ The coefficient of $x$ is $3$ which means the slope is $3.$

Also, when $x = 0, \, y=10+3(0),$ the value of $y$ is $10$ which means the $y$ -intercept is $10.$ Students can also rearrange the equation to be in slope intercept form to avoid confusion, $y=3 x+10.$

Practice y = mx + b questions

m=-5, \; b=9

m=5, \; b = 9

m=9, \; b =5

m=9, \; b=-5

The slope intercept form of a linear equation is $y=m x+b.$

In this case, $y=-5 x+9, \, m=-5$ and $b=9.$

The coefficient of the $x$ term is $-5$ so it is the slope.

If you make $x=0$ you can solve for the $y$ -intercept.

\begin{aligned}& y=-5(0)+9 \\\\ & y=9\end{aligned}

So the $y$ -intercept is $9.$

m=6, \; b=-1

m=1, \; b=6

m=-1, \; b=6

m=0, \; b=6

The slope intercept form of a linear equation is $y=m x+b.$

In this case, $y=6-x,$ which should be rewritten in the form of $y=m x+b.$

You can switch the terms and write the equation as $y=-x+6$ where $m=-1$ and $b=6.$

The coefficient of the $x$ term is $-1$ so it is the slope.

If you make $x=0$ you can solve for the $y$ -intercept.

\begin{aligned}& y=-1(0)+6 \\\\ & y=6\end{aligned}

So the $y$ -intercept is $6.$

b=6

m=2, \; b=5

m=\cfrac{1}{2}, \; b=-\cfrac{5}{2}

m=\cfrac{1}{2}, \; b=5

m=1, \; b=5

First put the equation in $y=m x+b$ form first which means to solve the equation for $y.$

\begin{aligned}& x=2 y+5 \\\\ & x-5=2 y+5-5 \\\\ & x-5=2 y \\\\ & \cfrac{x}{2}-\cfrac{5}{2}=\cfrac{2 y}{2} \end{aligned}

$\cfrac{x}{2}-\cfrac{5}{2}=y$ which is the same as $y=\cfrac{x}{2}-\cfrac{5}{2}$

Remember that $\cfrac{x}{2}=\cfrac{1}{2} \, x.$

So the slope $= m=\cfrac{1}{2}$ and the $y$ -intercept $= b=\cfrac{5}{2}=2 \cfrac{1}{2} \, .$

y=0 x-5

y=5 x-0

y=-5 x

y=x-5

The slope is given to be $-5$ and the $y$ -intercept is given to be $0.$

So, $m=-5$ and $b=0.$

Using those values, substitute them into $y=m x+b,$ which gives the equation $y=-5 x+0.$ That is the same as $y=-5 x.$

m=\cfrac{2}{3}, \; b=-3

m=2, \; b=0

m=6, \; b=9

m=\cfrac{2}{3}, \; b=3

First put the equation in $y=m x+b$ form first which means to solve the equation for $y.$

\begin{aligned}& 2 x=3(3+y) \\\\ & 2 x=9+3 y \\\\ & 2 x-9=9-9+3 y \\\\ & 2 x-9=3 y \\\\ & \cfrac{2 x}{3}-\cfrac{9}{3}=\cfrac{3 y}{3} \end{aligned}

$\cfrac{2 x}{3}-3=y$ which is the same as $y=\cfrac{2 x}{3}-3$

Remember that $\cfrac{2 x}{3}=\cfrac{2}{3} \, x.$

So the slope $= m=\cfrac{2}{3}$ and the $y$ -intercept $= b=-3.$

m=0.75, \; b=0.5

m=-\cfrac{2}{3}, \; b=\cfrac{1}{3}

m=\cfrac{1}{3}, \; b=\cfrac{2}{3}

m=1.5, \; b=0.5

First put the equation in $y=m x+b$ form first which means to solve the equation for $y.$

\begin{aligned}& 0.5 x+0.75 y=0.25 \\\\ & 0.5 x-0.5 x+0.75 y=-0.5 x+0.25 \\\\ & 0.75 y=-0.5 x+0.25 \\\\ & \cfrac{0.75 y}{0.75}=\cfrac{-0.5 x}{0.75}+\cfrac{0.25}{0.75} \\\\ & y=-0 . \overline{6} x+0 . \overline{3}\end{aligned}

Recall:

\begin{aligned}& -0 . \overline{6}=\cfrac{6}{9}=\cfrac{2}{3} \\\\ & 0 . \overline{3}=\cfrac{3}{9}=\cfrac{1}{3} \\\\ & \text { So, } y=-\cfrac{2}{3} \, x+\cfrac{1}{3}\end{aligned}

The slope $= m=-\cfrac{2}{3}$ (negative slope) and the $y$ -intercept $= b=\cfrac{1}{3}$

y = mx + b FAQs

What is the $\textbf{x}$ -intercept of a line?

The $x$ -intercept is the point where the line passes or crosses the $x$ -axis.

Is there a way of finding the slope if it is not given?

Yes, you can use the slope formula to find the slope of a line using two points on the line.

How do you calculate the slope using the formula?

To calculate the slope, subtract the $y$ -coordinates and the $x$ -coordinates, and write them as a quotient of the differences of the $y’s$ over the differences of the $x’s.$

What is the slope intercept equation?

The slope intercept equation is $y=m x+b,$ where $m$ represents the slope and $b$ represents the $y$ -intercept.

The next lessons are

Angles
Rate of change
Systems of equations
Number patterns

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.