1. Show $ x > 5 $ on a number line.

2. Show $ x\leq{7} $ on a number line.

3. Show $ \cfrac{3}{2} \, > x $ on a number line.

6. Maria’s mom said she could invite $ 15 $ friends at most to her birthday party. Which graph shows how many friends she can invite to her birthday party?

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Whole Numbers Integers Decimal number line Fractions Greater than sign Less than sign

Math resources Algebra Inequalities

Inequalities on a number Line

Inequalities on a number line

Here you will learn about inequalities on a number line, including how to represent inequalities on a number line, interpret inequalities from a number line, and list integer values from an inequality.

Students will first learn about inequalities on a number line as part of expressions and equations in 6th grade.

What are inequalities on a number line?

Inequalities on a number line allow us to visualize the values that are represented by an inequality.

To represent inequalities on a number line, we show the range of numbers by drawing a straight line and indicating the end points with either an open circle or a closed circle.

An open circle shows it does not include the value.

A closed circle shows it does include the value.

For example,

Show $x < 3$ on a number line.

An open circle needs to be indicated at $‘3’$ on the number line. This shows that the solution to the inequality does not include the value.

$x < 3$ is read $‘x$ is less than $3’,$ so the values to the left of the circle need to be indicated with a line.

You can also represent a graphed inequality with symbols.

For example,

Write the inequality shown on the number line.

The graph starts at $0$ and the closed circle shows us that $0$ is included in the solution set. The line shows that values less than $0$ are also included in the solution set.

Comparing $x$ to $0,$ the graph shows that $‘x$ is less than or equal to $0’ → x \leq 0$

Comparing $0$ to $x,$ the graph shows that $‘0$ is greater than or equal to $x' → 0 \geq x$

While the first inequality is how this relationship is typically written, always remember that the other statement is equal.

What are inequalities on a number line?

[FREE] Inequalities on a Number Line Worksheet (Grade 6)

Use this worksheet to check your 6th-grade students’ skills in graphing inequalities on a number line. 15 questions complete with answers to identify learning gaps!

DOWNLOAD FREE NOW

[FREE] Inequalities on a Number Line Worksheet (Grade 6)

Use this worksheet to check your 6th-grade students’ skills in graphing inequalities on a number line. 15 questions complete with answers to identify learning gaps!

DOWNLOAD FREE NOW

Common Core State Standards

How does this relate to 6th grade math?

Grade 6 – Expressions and Equations (6.EE.B.8)
Write an inequality of the form $x > c$ or $x < c$ to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form $x > c$ or $x < c$ have infinitely many solutions; represent solutions of such inequalities on number line diagrams.

How to graph inequalities on a number line

In order to graph inequalities on a number line:

Identify the starting value.
Decide if the starting value is included in the solution set.
Identify the solution set with a straight line.

Inequalities on a number line examples

Example 1: single values

Graph $x > 3$ on a number line.

Identify the starting value.

The inequality indicates that $3$ is the starting value.

2Decide if the starting value is included in the solution set.

Since the symbol is $>,$ the $3$ is not included in the solution, so the graph has an open circle.

Inequalities on a Number Line example 1 image 1

3Identify the solution set with a straight line.

$x > 3$ reads $‘x$ is greater than $3’,$ so the line is drawn to the right of the circle to show the solution set includes all values greater than $3.$

Inequalities on a Number Line example 1 image 2

Example 2: single values

Graph $-2\geq{x}$ on a number line.

Identify the starting value.

The inequality indicates that $-2$ is the starting value.

Decide if the starting value is included in the solution set.

Since the symbol is $\geq,$ the $-2$ is included in the solution, so the graph has a closed circle.

Inequalities on a Number Line example 2 image 1

Identify the solution set with a straight line.

$-2 \geq x$ reads $‘-2$ is greater than or equal to $x’,$ so the line is drawn to the left of the circle to show the solution set includes all values less than or equal to $-2.$

Inequalities on a Number Line example 2 image 2

*Note that you can also read the inequality $-2 \geq x$ from right to left as $‘x$ is less than or equal to $-2’$ .

Example 3: single values

Graph $8.5 \leq x$ on a number line.

Identify the starting value.

The inequality indicates that $8.5$ is the starting value.

Decide if the starting value is included in the solution set.

Since the symbol is $\leq,$ the $8.5$ is included in the solution, so the graph has a closed circle.

Inequalities on a Number Line example 3 image 1

Identify the solution set with a straight line.

$8.5 \leq x$ reads $‘8.5$ is less than or equal to $x’,$ so the line is drawn to the right of the circle to show the solution set includes all values greater than or equal to $8.5.$

Inequalities on a Number Line example 3 image 2

*Note that you can also read the inequality $8.5 \leq x$ from right to left as $‘x$ is greater than or equal to $8.5’$ .

Example 4: writing an inequality from a number line

Write the inequality that is shown on the number line.

Identify the starting value.

The inequality indicates that $4$ is the starting value.

Decide if the starting value is included in the solution set.

Since the circle is closed, $4$ is included in the solution set.

Identify the solution set with a straight line.

The line shows that values greater than $4$ are also included in the solution set.

This graph shows the inequalities:

$x \geq 4 → ‘x$ is greater than or equal to $4’$

and

$4 \leq x → ‘4$ is less than or equal to $x’$ .

Example 5: writing an inequality from a number line

Write the inequality that is shown on the number line.

Identify the starting value.

The inequality indicates that $-3$ is the starting value.

Decide if the starting value is included in the solution set.

Since the circle is open, $-3$ is not included in the solution set.

Identify the solution set with a straight line.

The line shows that values greater than $-3$ are included in the solution set.

This graph shows the inequalities:

$x < -3 \to ‘x$ is less than $-3’$

and

$-3 > x \to ‘ -3$ is greater than $x’$ .

Example 6: real world example

Maryam wants to spend at least $45$ minutes each week memorizing her lines for the upcoming play.

Create a graph that represents how much time she should spend memorizing lines each week.

Identify the starting value.

‘Maryam wants to spend at least $45$ minutes each week…’ $\to 45$ is the starting value.

Decide if the starting value is included in the solution set.

$45$ is included in the solution set, because ‘at least’ means $45$ and greater, so the graph has a closed circle.

Inequalities on a Number Line example 6 image 1

Identify the solution set with a straight line.

The line is drawn to the right of the circle to show the solution set also includes all values greater than $45.$

Inequalities on a Number Line example 6 image 2

Teaching tips for inequalities on a number line

To help students memorize the inequality symbols, make sure they are posted in the classroom or somewhere else easily accessible. Also encourage students to read inequalities both forward and backwards, which forces them to focus on the shape of the inequality symbol.

When introducing the $\leq$ and $\geq ,$ explicitly make the connection between these signs and the greater than, less than, and equal sign.

Number line worksheets are a good way to help students develop this skill, but be sure to also include activities that are more interactive. This could include graphing inequalities digitally or using things that happen in and around the classroom as a basis for writing and graphing real world inequalities.

Easy mistakes to make

Confusing when to include or not include the starting value
Open circles do not include the value in the solution set and require a $‘<’$ or $‘>’$ sign. Closed circle do include the value in the solution set and require a $‘\leq’$ or a $‘\geq’$ sign.

Making the incorrect interpretation when the variable is on the right side
The direction of the inequality sign shows if the solution set is ‘greater than’ or ‘less than’. This can be confused when both sides of the inequality are switched.
For example,
$x > 8$ is the same as $8 < x$ .
In both, $x$ is greater than $8$ as the inequality sign is open towards the $x.$

Confusing the meaning of the phrases ‘at least’ and ‘at most’
‘At least’ includes the given number and everything above. ‘At most’ includes the given number and everything below. It is easy to think least means below and most means above, but you must consider these words within the context.
For example,
The weatherman says, at most the temperature will reach $7$ degrees. This means $‘7$ degrees or less’ or ‘no more than $7$ degrees’, so the inequality graph is…

Practice inequalities on a number line questions

Inequalities on a Number Line prac question 1 image 1

Inequalities on a Number Line prac question 1 image 2

Inequalities on a Number Line prac question 1 image 3

Inequalities on a Number Line prac question 1 image 4

$x > 5$ is read $‘x$ is greater than $5.’$ The starting value is not included in the solution set, so an open circle is used.

The solution set is all values greater than $5,$ so the line is to the right of the circle.

Inequalities on a Number Line prac question 2 image 1

Inequalities on a Number Line prac question 2 image 2

Inequalities on a Number Line prac question 2 image 3

Inequalities on a Number Line prac question 2 image 4

$x \leq 7$ is read $‘x$ is less than or equal to $7.’$ The starting value is included in the solution set, so a closed circle is used.

The solution set also includes all values less than $7,$ so the line is to the left of the circle.

Inequalities on a Number Line prac question 3 image 1

Inequalities on a Number Line prac question 3 image 2

Inequalities on a Number Line prac question 3 image 3

Inequalities on a Number Line prac question 3 image 4

$\cfrac{3}{2} \, > x$ is read $‘ \, \cfrac{3}{2} \,$ is greater than $x.’$

From right to left the inequality is read $‘x$ is less than $\, \cfrac{3}{2} \, .’$

The starting value is not included in the solution set, so an open circle is used.

The solution set includes all values less than $\, \cfrac{3}{2} \, ,$ so the line is to the left of the circle.

The circle is at $\, \cfrac{3}{2} \,$ or $1 \, \cfrac{1}{2} \, .$

x < 6

x \leq 6

x > 6

x \geq 6

$6$ is indicated with a closed circle so this value is included in the solution set.

The arrow is drawn to the left side to indicate values less than $6.$

The graph shows $x \leq 6.$

x < -9

x \leq -9

x > -9

x \geq -9

$-9$ is indicated with an open circle so this value is not included in the solution set.

The arrow is drawn to the right side to indicate values greater than $-9.$

The graph shows $x > -9.$

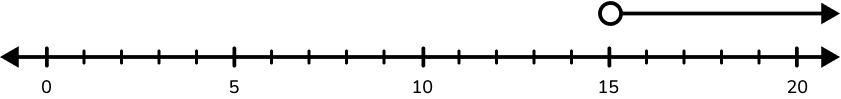
Inequalities on a Number Line prac question 6 image 1

Inequalities on a Number Line prac question 6 image 2

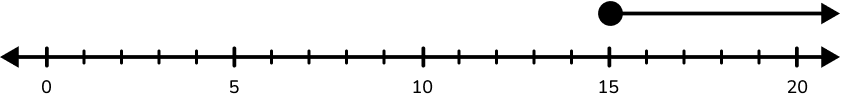
Inequalities on a Number Line prac question 6 image 3

Inequalities on a Number Line prac question 6 image 4

‘Maria’s mom said she could invite $15$ friends at most…’ $\to 15$ is the starting value.

$15$ is included in the solution set, because ‘at most’ means $15$ and less, so the graph has a closed circle.

The line is drawn to the left of the circle to show the solution set also includes all values less than $15.$

Inequalities on a number line FAQs

Do all inequalities only have one variable?

No, just like expressions and equations, inequalities increasingly get more complex as students advance in their math learning. In 7th grade, students will continue learning by working with linear inequalities, also known as two-step inequalities.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.