7. Represent the solution on a number line. $ 5x-2 < 28 $

Solving Inequalities - Math Steps, Examples & Questions

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

Algebraic expressions Integers Fractions Combining like terms

Math resources Algebra Inequalities

Solving inequalities

Here you will learn about solving inequalities, including how to solve linear inequalities, identify integers in the solution set, and represent solutions on a number line.

Students will first learn about solving simple inequalities as part of expressions and equations in 6th grade math and expand that knowledge in 7th grade math.

What is solving inequalities?

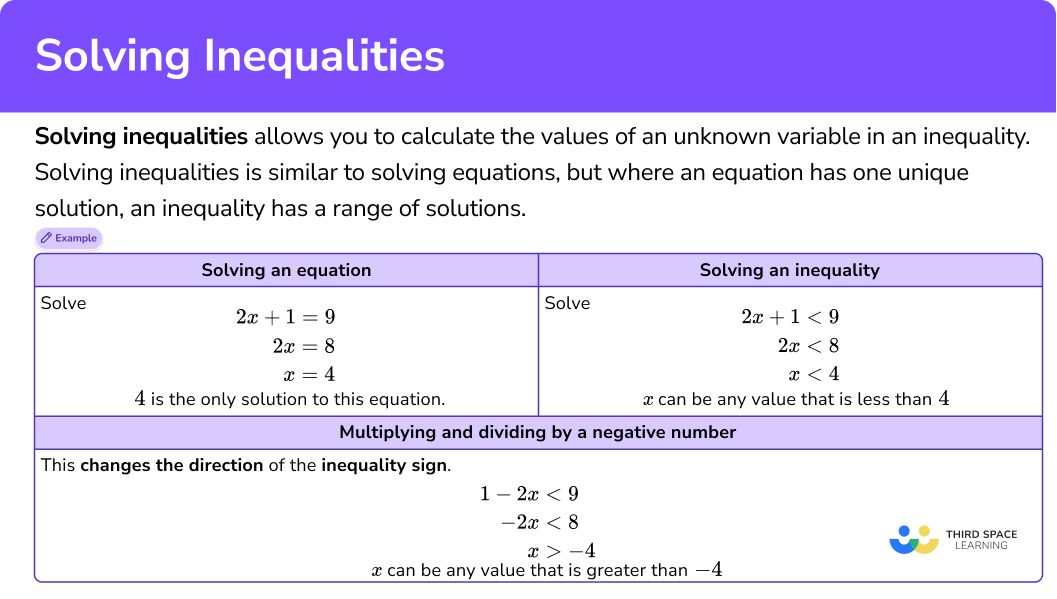
Solving inequalities allows you to calculate the values of an unknown variable in an inequality.

Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions.

In order to solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

For example,

Solving an equation	Solving an inequality
Solve $\begin{aligned} 2x + 1 &= 9 \\ 2x &= 8 \\ x&= 4 \end{aligned}$ $4$ is the only solution to this equation.	Solve $\begin{aligned} 2x + 1 &< 9 \\ 2x &< 8 \\ x&< 4 \end{aligned}$ $x$ can be any value that is less than $4.$

Solving an equation

Solving an inequality

Solve

\begin{aligned} 2x + 1 &= 9 \\ 2x &= 8 \\ x&= 4 \end{aligned}

$4$ is the only solution to this
equation.

Solve

\begin{aligned} 2x + 1 &< 9 \\ 2x &< 8 \\ x&< 4 \end{aligned}

$x$ can be any value that is less
than $4.$

Multiplying and dividing by a negative number
This changes the direction of the inequality sign. For example, $\begin{aligned} 1 - 2x &< 9 \\ -2x &< 8 \\ x&> -4 \end{aligned}$ $x$ can be any value that is greater than $-4.$

Multiplying and dividing by a negative number

This changes the direction of the inequality sign.
For example,

\begin{aligned} 1 - 2x &< 9 \\ -2x &< 8 \\ x&> -4 \end{aligned}

$x$ can be any value that is greater than $-4.$

What is solving inequalities?

Common Core State Standards

How does this relate to 6th grade and 7th grade math?

Grade 6 – Expressions and Equations (6.EE.B.8)
Write an inequality of the form $x > c$ or $x < c$ to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form $x > c$ or $x < c$ have infinitely many solutions; represent solutions of such inequalities on number line diagrams.

Grade 7 – Expressions and Equations (7.EE.4b)
Solve word problems leading to inequalities of the form $px + q > r$ or $px + q < r,$ where $p, q,$ and $r$ are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem.
For example: As a salesperson, you are paid $\$50$ per week plus $\$3$ per sale. This week you want your pay to be at least $\$100.$ Write an inequality for the number of sales you need to make, and describe the solutions.

How to solve inequalities

In order to solve inequalities:

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.
Write your solution with the inequality symbol.

[FREE] Solving Inequalities Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving inequalities. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Solving Inequalities Worksheet (Grade 6 to 8)

Use this worksheet to check your grade 6 to 8 students’ understanding of solving inequalities. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

Solving linear inequalities examples

Example 1: solving linear inequalities

Solve:

$4 x+6<26$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you are subtracting $6$ from both sides.

$\begin{aligned} 4x+6&<26\\ 4x&<20 \end{aligned}$

This leaves $4x$ on the left side of the inequality sign and $20$ on the right side.

2Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $4.$

$\begin{aligned} 4x&<20\\ x&<5 \end{aligned}$

This leaves $x$ on the left side of the inequality sign and $5$ on the right side.

3Write your solution with the inequality symbol.

$x < 5$

Any value less than $5$ satisfies the inequality.

Example 2: solving linear inequalities

Solve:

$5x-4 \geq 26$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to add $4$ to both sides.

$\begin{aligned} 5x-4&\geq26\\ 5x&\geq30 \end{aligned}$

This leaves $5x$ on the left side of the inequality sign and $30$ on the right side.

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $5.$

$\begin{aligned} 5x&\geq30\\ x&\geq6 \end{aligned}$

This leaves $x$ on the left side of the inequality sign and $6$ on the right side.

Write your solution with the inequality symbol.

$x\geq6$

Any value greater than or equal to $6$ satisfies the inequality.

Example 3: solving linear inequalities with parentheses

Solve:

$3(x-4)\leq12$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

Let’s start by expanding the parentheses.

$3x-12\leq12$

Then you need to add $12$ to both sides.

$\begin{aligned} 3x-12&\leq12\\ 3x&\leq24 \end{aligned}$

This leaves $3x$ on the left side of the inequality sign and $24$ on the right side.

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $3.$

$\begin{aligned} 3x&\leq24\\ x&\leq8 \end{aligned}$

This leaves $x$ on the left side of the inequality sign and $8$ on the right side.

Write your solution with the inequality symbol.

$x\leq8$

Any value less than or equal to $8$ satisfies the inequality.

Example 4: solving linear inequalities with unknowns on both sides

Solve:

$5x-6 > 2x + 15$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to subtract $2x$ from both sides.

$\begin{aligned} 5x-6&>2x+15\\ 3x-6&>15 \end{aligned}$

This leaves $3x-6$ on the left side of the inequality sign and $15$ on the right side.

Rearrange the inequality so that $\textbf{‘x’}$ s are on one side of the inequality sign and numbers on the other.

In this case you need to add $6$ to both sides.

$\begin{aligned} 3x-6&>15\\ 3x&>21 \end{aligned}$

This leaves $3x$ on the left side of the inequality sign and $21$ on the right side.

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $3.$

$\begin{aligned} 3x&>21\\ x&>7 \end{aligned}$

This leaves $x$ on the left side of the inequality sign and $7$ on the right side.

Write your solution with the inequality symbol.

$x > 7$

Any value greater than $7$ satisfies the inequality.

Example 5: solving linear inequalities with fractions

Solve:

$\cfrac{x+3}{5}<2$

Rearrange the inequality to eliminate the denominator.

In this case you need to multiply both sides by $5.$

$\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10 \end{aligned}$

Rearrange the inequality so that $\textbf{‘x’}$ s are on one side of the inequality sign and numbers on the other.

In this case you need to subtract $3$ from both sides.

$\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10\\ x&<7 \end{aligned}$

Write your solution with the inequality symbol.

$x < 7$

Any value less than $7$ satisfies the inequality.

Example 6: solving linear inequalities with non-integer solutions

Solve:

$6x+1\geq4$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to subtract $6$ from both sides.

$\begin{aligned} 6x+1&\geq4\\ 6x&\geq3 \end{aligned}$

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $6.$

$\begin{aligned} 6x+1&\geq4\\ 6x&\geq3\\ x&\geq\cfrac{3}{6} \end{aligned}$

This can be simplified to $\, \cfrac{1}{2} \,$ or the decimal equivalent.

Write your solution with the inequality symbol.

$x\geq\cfrac{1}{2}$

Any value greater than or equal to $\, \cfrac{1}{2} \,$ satisfies the inequality.

Example 7: solving linear inequalities and representing solutions on a number line

Represent the solution on a number line:

$2x-7 < 5$

Rearrange the inequality so that $\textbf{‘x’}$ s are on one side of the inequality sign and numbers on the other.

In this case you need to add $7$ to both sides.

$\begin{aligned} 2x-7&<5\\ 2x&<12 \end{aligned}$

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by $2.$

$\begin{aligned} 2x-7& <5\\ 2x& <12\\ x& < 6 \end{aligned}$

Represent your solution on a number line.

$x <6$

Any value less than $6$ satisfies the inequality. An open circle is required at $6$ and the values lower than $6$ indicated with an arrow.

Example 8: solving linear inequalities with negative x coefficients

Solve:

$1-2x <7$

Rearrange the inequality so that $\textbf{‘x’}$ s are on one side of the inequality sign and numbers on the other.

In this case you need to subtract $1$ from both sides.

$\begin{aligned} 1-2x & <7 \\ -2x & <6 \end{aligned}$

Rearrange the inequality by dividing by the $\textbf{x}$ coefficient so that $\textbf{‘x’}$ is isolated.

In this case you need to divide both sides by negative $2.$

$6 \div-2=-3$

Change the direction of the inequality sign.

Because you divided by a negative number, you also need to change the direction of the inequality sign.

$\begin{aligned} 1-2x & <7 \\ -2x & <6 \\ x &>-3 \end{aligned}$

Example 9: solving linear inequalities and listing integer values that satisfy the inequality

List the integer values that satisfy:

$3 < x+1\leq8$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to subtract $1$ from each part.

$\begin{aligned} 3&<x+1\leq8\\ 2&<x\leq7\\ \end{aligned}$

List the integer values satisfied by the inequality.

$2<x\leq7$

$2$ is not included in the solution set. $7$ is included in the solution set. The integers that satisfy this inequality are:

$3, 4, 5, 6, 7$

Example 10: solving linear inequalities and listing integer values that satisfy the inequality

List the integer values that satisfy:

$7\leq4x\leq20$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to divide each part by $4.$

$\begin{aligned} 7\leq \, & 4x\leq20\\ \cfrac{7}{4}\leq & \; x \leq5 \end{aligned}$

List the integer values satisfied by the inequality.

$\cfrac{7}{4} \leq x \leq 5$

$\cfrac{7}{4} \,$ is included in the solution set but it is not an integer.

The first integer higher is $2.$

$5$ is also included in the solution set.

The integers that satisfy this inequality are:

$2, 3, 4, 5$

Example 11: solving linear inequalities and representing the solution on a number line

List the integer values that satisfy:

$-3<2x+5\leq7$

Rearrange the inequality so that all the unknowns are on one side of the inequality sign.

In this case you need to subtract $5$ from each part.

$\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2 \end{aligned}$

Rearrange the inequality so that $\textbf{‘x’}$ is isolated. In this case you need to divide each part by $\bf{2}$ .

$\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2\\ -4<x&\leq1 \end{aligned}$

Represent the solution set on a the number line

$-4<x\leq1$

$-4$ is not included in the solution set so requires an open circle. $1$ is included in the solution set so requires a closed circle.

Put a solid line between the circles to indicate all the values that satisfy the solution set.

Teaching tips for solving inequalities

Students should master solving simple inequalities (one-step inequalities) before moving on to two-step inequalities (or multi-step inequalities).

Foster student engagement by practicing solving inequalities through classroom games such as BINGO rather than daily worksheets.

Student practice problems should have a variety of inequalities such as inequalities with fractions, negative numbers, and parentheses. (see examples above)

Easy mistakes to make

Solutions as inequalities
Not including the inequality symbol in the solution is a common mistake. An inequality has a range of values that satisfy it rather than a unique solution so the inequality symbol is essential.

For example, when solving $x + 3 < 7$ giving a solution of $4$ or $x = 4$ is incorrect, the answer must be written as an inequality $x < 4$ .

Balancing inequalities
Errors can be made with solving equations and inequalities by not applying inverse operations or not balancing the inequalities. Work should be shown step-by-step with the inverse operations applied to both sides of the inequality.

For example, when solving $x + 3 < 7 ,$ adding $3$ to both sides rather than subtracting $3$ from both sides.

Practice solving inequalities questions

3x < 24

x > 8

8

x<8

$\begin{aligned} 3x+7&<31\\ 3x&<24\\ x&<8 \end{aligned}$

x < 7

x \geq 7

x > 7

7

$\begin{aligned} 4x-3&\geq25\\ 4x&\geq28\\ x&\geq7 \end{aligned}$

x < 9

x \leq-1

x \leq9

9

$\begin{aligned} 2(x-5)&\leq8\\ 2x-10&\leq8\\ 2x&\leq18\\ x&\leq9 \end{aligned}$

x > 3

x < 3.5

x \leq 3

3

$\begin{aligned} 6x-5&>4x+1\\ 2x-5&>1\\ 2x&>6\\ x&>3 \end{aligned}$

x < 4

x > 16

x\leq3

16

$\begin{aligned} \cfrac{x-4}{2}&>6\\ x-4&>12\\ x&>16 \end{aligned}$

x\geq 4

x\leq4

\cfrac{1}{4}

x\geq \, \cfrac{1}{4}

$\begin{aligned} 8x+1&\geq3\\ 8x&\geq2\\ x&\geq\cfrac{2}{8}\\ x&\geq\cfrac{1}{4} \end{aligned}$

Solving Inequalities prac question 7 image 2

Solving Inequalities prac question 7 image 3

Solving Inequalities prac question 7 image 4

Solving Inequalities prac question 7 image 5

$\begin{aligned} 5x-2&<28\\ 5x&<30\\ x&<6 \end{aligned}$

An open circle is required and all values less than $6$ indicated.

x > 4

x < -4

-x > 4

x < \, \cfrac{16}{3}

$\begin{aligned} 2-3x &>14 \\ -3x &>12 \\ x &< -4 \end{aligned}$

Change the direction of the inequality sign as you have divided by a negative number.

0, 1, 2

2, 3, 4, 5

3, 4, 5

-1, 0, 1, 2

$\begin{aligned} 2<x&+3\leq5\\ -1< \, &x\leq2 \end{aligned}$

$-1$ is not included in the solution set as is greater than $-1.$

$2$ is included in the solution set as $x$ is less than or equal to $2.$

1, 2, 3, 4, 5, 6, 7

2, 3, 4, 5, 6

1, 2, 3, 4, 5, 6

2, 3, 4, 5, 6, 7

$\begin{aligned} 4\leq3&x\leq21\\ \cfrac{4}{3} \, \leq \, &x\leq7 \end{aligned}$

The first integer greater than $\, \cfrac{4}{3} \,$ is $2.$

$7$ is included in the solution set as $x$ is less than or equal to $7.$

-2, -1, 0, 1

-1, 0

-1, 0, 1

-3, -2, -1, 0, 1, 2, 3, 4, 5

$\begin{aligned} -4<3x&+2\leq5\\ -6<3&x\leq3\\ -2< \, &x\leq1 \end{aligned}$

$-2$ is not included in the solution set as $x$ is greater than $-2.$

$1$ is included in the solution set as $x$ is less than or equal to $1.$

Solving inequalities FAQs

What is solving inequalities?

Solving inequalities is where you calculate the values that an unknown variable can be in an inequality.

How do you solve an inequality?

To solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.

How does solving inequalities differ from solving equations?

Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.