Geometric Sequence Formula - Math Steps, Examples & Question

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Multiplication and division Absolute value Substitution Sequences

Math resources Algebra Number patterns

Geometric sequence formula

Here you will learn what geometric sequences are, how to continue a geometric sequence, how to generate a geometric sequence formula and how to translate between recursive and explicit formulas.

Students will first learn about geometric sequence formula as part of algebra in high school.

What are geometric sequences?

Geometric sequences are ordered sets of numbers that progress by multiplying or dividing each term by a common ratio.

If you multiply or divide by the same number each time to make the sequence, it is a geometric sequence.

The common ratio is the same for any two consecutive terms.

For example,

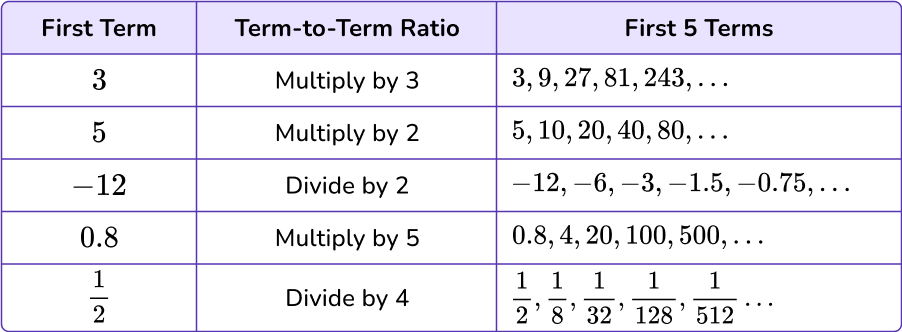
The geometric sequence recursive formula is:

a_{n+1}=r \cdot a_n

Where,

$a_{n}$ is the $n$ th term (general term)

$a_{n+1}$ is the term after $n$

$n$ is the term position

$r$ is the common ratio

The recursive formula calculates the next term of a geometric sequence, $n+1,$ based on the previous term, $n.$

The geometric sequence explicit formula is:

a_{n}=a_{1}(r)^{n-1}

Where,

$a_{n}$ is the $n$ th term (general term)

$a_{1}$ is the first term

$n$ is the term position

$r$ is the common ratio

The explicit formula calculates the $n$ th term of a geometric sequence, given the term number, $n.$

You create both geometric sequence formulas by looking at the following example:

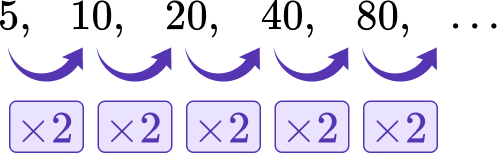
You can see the common ratio $(r)$ is $2,$ so $r=2.$

The recursive formula is $a_{n+1}=2 \cdot a_n,$ for $a_1=5.$

\begin{aligned}& a_2=2 \cdot a_1=2 \cdot 5=10 \\\\ & a_3=2 \cdot a_2=2 \cdot 10=20 \\\\ & a_4=2 \cdot a_3=2 \cdot 20=40 \\\\ & a_5=2 \cdot a_4=2 \cdot 40=80 \end{aligned}

The explicit formula is $a_n=5(2)^{n-1}.$

\begin{aligned}& a_2=5(2)^{2-1}=5(2)^1=5 \cdot 2=10 \\\\ & a_3=5(2)^{3-1}=5(2)^2=5 \cdot 4=20 \\\\ & a_4=5(2)^{4-1}=5(2)^3=5 \cdot 8=40 \\\\ & a_5=5(2)^{5-1}=5(2)^4=5 \cdot 16=80 \end{aligned}

What are Geometric Sequences?

Common Core State Standards

How does this relate to high school math?

Functions – Building Functions (HSF.BF.A.2)
Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.

Functions – Linear, Quadratic and Exponential Models (HSF.LE.A.2)
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).

[FREE] Geometric Sequence Formula Worksheet (Grade 9 to 12)

Use this worksheet to check your grade 9 to 12 students’ understanding of geometric sequence formula. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Geometric Sequence Formula Worksheet (Grade 9 to 12)

Use this worksheet to check your grade 9 to 12 students’ understanding of geometric sequence formula. 15 questions with answers to identify areas of strength and support!

DOWNLOAD FREE

How to continue a geometric sequence

To continue a geometric sequence:

To identify $\textbf{r},$ take two consecutive terms from the sequence.
Divide the second term by the first term to find the common ratio $\textbf{r}.$
Multiply the last term in the sequence by the common ratio to find the next term.
Repeat Step $\bf{3}$ for each new term.

Geometric sequence examples

Example 1: continuing a geometric sequence given a graph

Calculate the next three terms for the geometric sequence shown in the graph below.

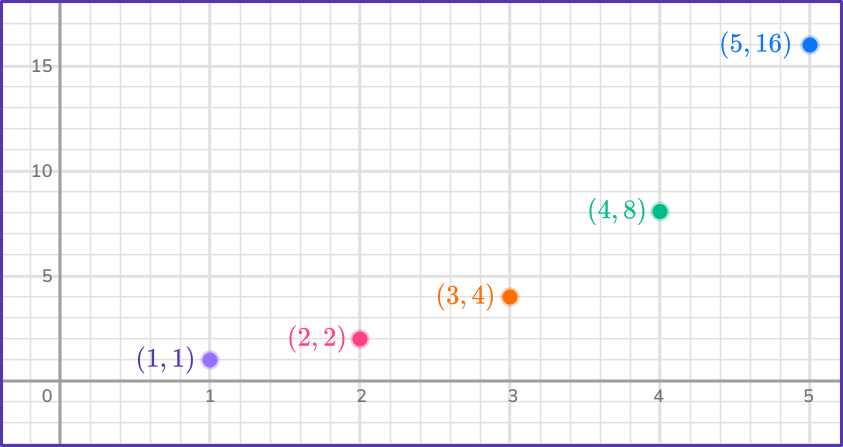
To identify $\textbf{r},$ take two consecutive terms from the sequence.

There are $5$ terms shown. Any two consecutive terms of a geometric sequence can be used. Let’s use the third term and the fourth term: $(3,4)$ and $(4,8).$

The $x$ coordinate is the term position (first, second, third, etc.). The $y$ coordinate is the actual term value.

So $(3,4)$ is $a_3=4$ and $(4,8)$ is the $a_4=8.$

2Divide the second term by the first term to find the common ratio $\textbf{r}.$

\begin{aligned}r&=8 \div 4 \\\\ r&=2 \end{aligned}

3Multiply the last term in the sequence by the common ratio to find the next term.

16 \times 2=32

4Repeat Step $\bf{3}$ for each new term.

\begin{aligned}& 32 \times 2=64 \\\\ & 64 \times 2=128\end{aligned}

The next three terms in the sequence are $32, 64,$ and $128.$

Example 2: continuing a geometric sequence given a table

Calculate the next three terms for the sequence in the table below.

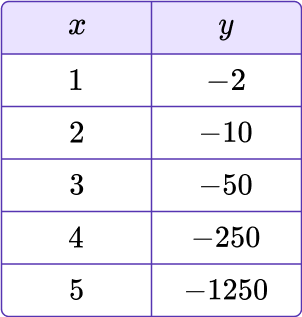
To identify $\textbf{r},$ take two consecutive terms from the sequence.

There are $5$ terms shown. Any two consecutive terms of a geometric sequence can be used. Let’s use the second term and the third term: $(2,-10)$ and $(3,-50).$

In the table, the $x$ value is the term position (first, second, third, etc.). The $y$ value is the actual term value.

Divide the second term by the first term to find the common ratio $\textbf{r}.$

\begin{aligned}r&=-50 \div -10 \\\\ r&=5 \end{aligned}

Multiply the last term in the sequence by the common ratio to find the next term.

-1250 \times 5=-6,250

Repeat Step $\bf{3}$ for each new term.

\begin{aligned}& -6250 \times 5=-31,250 \\\\ & -31250 \times 5=-156,250\end{aligned}

The next three terms are $-6,250, -31,250,$ and $-156,250.$

How to find a formula for a geometric sequence

In order to find a formula for a geometric sequence:

Identify the first term.
Divide the second term by the first term to find the common ratio, $\textbf{r}$ .
Write the recursive formula, $\bf{\textbf{a}}_{\textbf{n}+1}={\textbf{r}} {\textbf{a}}_{\textbf{n}}$ .
Write the explicit formula, $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1 (\textbf{r})^{\textbf{n}-1}}$ .

Example 3: writing formulas given a sequence with decimals

Write the recursive and explicit formula for the sequence below.

100, \, 10, \, 1, \, 0.1, \, 0.01, …

Identify the first term.

a_1=100

Divide the second term by the first term to find the common ratio, $\textbf{r}.$

\begin{aligned}& r=10 \div 100 \\\\ & r=0.1\end{aligned}

Write the recursive formula, $\bf{\textbf{a}}_{\textbf{n}+1}={\textbf{r}} {\textbf{a}}_{\textbf{n}}.$

Replace $r$ with $0.1$ in the formula.

$a_{n+1}=0.1 a_n$

Write the explicit formula, $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1 (\textbf{r})^{\textbf{n}-1}}$ .

Replace $a_1$ with $100$ and $r$ with $0.1$ in the formula.

$a_n=100(0.1)^{n-1}$

Example 4: writing formulas given a sequence with fractions

Write the recursive and explicit formula for the sequence below.

10, \, 5, \, 2 \cfrac{1}{2} \, , \, 1 \cfrac{1}{4} \, , \, \cfrac{5}{8} \ldots

Identify the first term.

a_1=10

Divide the second term by the first term to find the common ratio, $\textbf{r}.$

\begin{aligned}& r=5 \div 10 \\\\ & r=\cfrac{1}{2}\end{aligned}

Write the recursive formula, $\bf{\textbf{a}}_{\textbf{n}+1}={\textbf{r}} {\textbf{a}}_{\textbf{n}}.$

Replace $r$ with $\cfrac{1}{2}$ in the formula.

$a_{n+1}=\cfrac{1}{2} \, a_n$

Write the explicit formula, $\bf{\textbf{a}_\textbf{n}=\textbf{a}_1 (\textbf{r})^{\textbf{n}-1}}$ .

Replace $a_1$ with $10$ and $r$ with $\cfrac{1}{2}$ in the formula.

$a_n=10\left(\cfrac{1}{2}\right)^{n-1}$

How to translate between recursive and explicit formulas

In order to translate between recursive and explicit formulas:

Identify the common ratio, $\textbf{r}$ and first term, $\bf{\textbf{a}_1}.$
Rewrite the formula.

Example 5: translate between recursive and explicit

The recursive formula for a geometric sequence is $a_{n+1}=-4 a_n$ and $a_1=3.$ What is the explicit formula?

Identify the common ratio, $\textbf{r}$ and first term, $\bf{\textbf{a}_1}.$

$r$ is the coefficient in the recursive formula, so $r=-4$ and $a_1=3.$

Rewrite the formula.

The explicit formula of a geometric sequence is $a_n=a_1(r)^{n-1}.$

The explicit formula for this sequence is $a_n=3(-4)^{n-1}.$

Example 6: translate between explicit and recursive

The explicit formula for a geometric sequence is $a_n=-3(2.5)^{n-1}.$ What is the recursive formula?

Identify the common ratio, $\textbf{r}$ and first term, $\bf{\textbf{a}_1}.$

$a_1$ is the coefficient in the explicit formula, so $a_1=-3.$

$r$ is the base of the exponent in the explicit formula, so $r=2.5.$

Rewrite the formula.

The recursive formula of a geometric sequence is $a_{n+1}=r a_n.$

The recursive formula for this sequence is $a_{n+1}=2.5 a_n$ and $a_1=-3.$

Note: Always define $a_1$ with the recursive formula.

Teaching tips for geometric sequence formula

Spend time letting students explore the tables and graphs of geometric sequences to compare and contrast how different values for $a_1$ and $r$ impact the sequence.

Easy mistakes to make

Mixing up the common ratio of a geometric sequence with the common difference for arithmetic sequences
Although these two phrases are similar, each type of sequence is different. The successive term in a geometric sequence of numbers is calculated by multiplying the previous term by a common ratio and not by adding a common difference.

Misunderstanding sequence notation
It can be easy to confuse sequence notation with other types of mathematical notation, such as exponential notation. The first term of the sequence should always be defined, and is often $a_1.$

If $a_1$ is the first term, the successive terms of the geometric sequence follow this same pattern. Such as the $10$ th term, which is $a_{10}.$ This is NOT the same as $a^{10},$ which is $a$ to the power of $10,$ an exponent.

For example,
$a_n$ is the nth term, $a_{n+1}$ is the next term, and $a_{n-1}$ is the preceding term.
So a sequence looks like: $a_1, a_2, \ldots, a_{n-1}, a_n, a_{n+1}, \ldots$

Thinking a negative value for r means that all terms in the sequence are negative
This is not always the case as when the constant ratio, $r,$ is raised to an even power, the product of the exponent is always positive.

For example,
If the value of the common ratio, $r,$ is $-2$ and the first term is $1,$ the first five terms of the sequence are: $1, -2, 4, -8, 16.$

Incorrect simplifying of the $\bf{\textbf{n}}^{\textbf{th}}$ term
Unless the first term is $1,$ it cannot be multiplied by the base of the exponent, following the order of operations.

For example,
$6 \times 3^{n-1}$ is not equivalent to $18^{n-1}.$
$6 \times 3^{n-1}$ cannot be simplified any further.

Practice geometric sequence questions

1000, 5000, 10000

950, 1400, 1850

5000, 50000, 500000

550, 555, 560

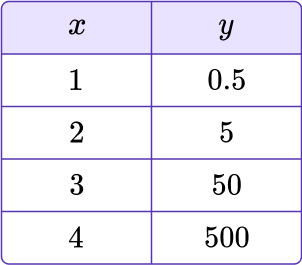
In the table, the $x$ value is the term position (first, second, third, etc.).

The $y$ value is the actual term value.

There are $4$ terms shown. Any two consecutive terms of a geometric sequence can be used to find the common ratio.

Let’s use the second term and the third term: $(2,5)$ and $(3,50).$

Common ratio:

50\div 5=10

Use the common ratio to calculate the next three terms.

\begin{aligned}& 500 \times 10=5000 \\\\ & 5000 \times 10=50000 \\\\ & 50000 \times 10=500000\end{aligned}

50, 100, 200

125, 625, 3125

50, 1000, 20000

12.5, 6.25, 3.125

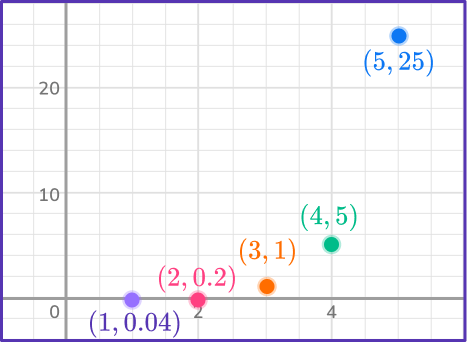
In the graph, the $x$ coordinate is the term position (first, second, third, etc.). The $y$ coordinate is the actual term value.

There are $5$ terms shown. Any two consecutive terms of a geometric sequence can be used to find the common ratio. Let’s use the fourth term and the fifth term: $(4,5)$ and $(5,25).$

Common ratio:

25\div 5=5

Use the common ratio to calculate the next three terms.

\begin{aligned}&\begin{aligned}& 25 \times 5=125 \\\\ & 125 \times 5=625\end{aligned} \\\\ &625 \times 5=3125\end{aligned}

a_n=(-3)^{n-1}

a_{n+1}=3(-1)^n

a_{n+1}=-1(-3)^n

a_n=-1(3)^{n-1}

Identify the first term.

a_1=-1

Choose two consecutive terms: $-27$ and $-9$

Common ratio:

-27 \div-9=3

Write the geometric explicit formula, $a_n=a_1(r)^{n-1}.$

Replace $a_1$ with $-1$ and $r$ with $3$ in the formula.

a_n=-1(3)^{n-1}

$a_{n+1}=\cfrac{1}{3} \, a_n$ and $a_1=36$

$a_n=3 a_{n+1}$ and $a_1=36$

$a_{n+1}=a_n+\cfrac{1}{3}$ and $a_1=36$

$a_n=\cfrac{1}{3} \, a_n$ and $a_1=36$

Identify the first term.

a_1=36

Choose two consecutive terms: $12$ and $4$

Common ratio:

4\div 12=\cfrac{1}{3}

Write the geometric recursive formula, $a_{n+1}=r a_n.$

Replace $r$ with $\cfrac{1}{3}$ in the formula.

a_{n+1}=\cfrac{1}{3} \, a_n

a_{n+1}=-88+0.9 a_n

a_{n+1}=0.9(-88)^{n-1}

a_n=-88(0.9)^{n-1}

$a_n=\cfrac{1}{3} \, a_n$ and $a_1=36$

$r$ is the coefficient in the recursive formula, so $r=0.9$ and $a_1=-88.$

The explicit formula of a geometric sequence is $a_n=a_1(r)^{n-1}.$

The explicit formula for this sequence is $a_n=-88(0.9)^{n-1}.$

$a_{n+1}=\cfrac{1}{2} \, a_n$ and $a_1=-1$

a_{n+1}=-1\left(\cfrac{1}{2}\right)^n

a_{n+1}=-1\left(\cfrac{1}{2} \, a_n\right)

-1, \,-\cfrac{1}{2} \, , \, -\cfrac{1}{4} \, , \, -\cfrac{1}{8} \, , \, -\cfrac{1}{16}

$a_1$ is the coefficient in the explicit formula, so $a_1=-1.$

$r$ is the base of the exponent in the explicit formula, so $r=\cfrac{1}{2} \, .$

The recursive formula of a geometric sequence is $a_{n+1}=r a_n.$

The recursive formula for this sequence is $a_{n+1}=\cfrac{1}{2} \, a_n$ and $a_1=-1.$

AND

$a_n=-1\left(\cfrac{1}{2}\right)^{n-1}$ is equal to $a_{n+1}=-1\left(\cfrac{1}{2}\right)^{n},$ because the input for both formulas is the previous term and the output is the next term.

AND

The first five terms:

\begin{aligned}& a_1=-1\left(\cfrac{1}{2}\right)^{1-1}=-1\left(\cfrac{1}{2}\right)^0=-1 \\\\ & a_2=-1\left(\cfrac{1}{2}\right)^{2-1}=-1\left(\cfrac{1}{2}\right)^1=-\cfrac{1}{2} \\\\ & a_3=-1\left(\cfrac{1}{2}\right)^{3-1}=-1\left(\cfrac{1}{2}\right)^2=-\cfrac{1}{4} \\\\ & a_4=-1\left(\cfrac{1}{2}\right)^{4-1}=-1\left(\cfrac{1}{2}\right)^3=-\cfrac{1}{8} \\\\ & a_5=-1\left(\cfrac{1}{2}\right)^{5-1}=-1\left(\cfrac{1}{2}\right)^4=-\cfrac{1}{16}\end{aligned}

Geometric sequence formula FAQs

What is the difference between the recursive formula and the explicit formula?

The recursive formula requires the term before it to calculate the next term. The explicit formula uses the term position to calculate the term value.

What is a geometric series?

The sum of the terms in a geometric sequence (geometric progression) is a geometric series. It can be the sum of an infinite geometric sequence, from $n=1$ to $\infty$ (know as an infinite geometric series) or a range of terms, such as the sum of the first $n$ terms, where $n$ is the number of terms included in the series.

The next topics are:

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.