What Is An Acute Triangle? An Explanation And Examples For Teachers And Students

Acute triangles are introduced to students in 4th grade. Although students learn about geometric shapes in kindergarten, they only begin to categorize triangles, including acute triangles, in fourth grade. This is based on two attributes: side lengths and angles.

Learning about geometric shapes, such as acute triangles, is extremely important because it connects math to the physical world and supports mathematical thinking in areas such as engineering, and physical sciences. 

This blog explores the knowledge students gain about the properties of acute triangles in fourth grade to using Heron’s formula and Pythagorean theorem in middle school through to trigonometry in high school. 

What is an acute triangle?

An acute triangle is a triangle with all acute angles (angles that measure less than 90 degrees). Acute triangles are classified as polygons – any two-dimensional, closed shape made of straight lines. 

Acute triangles can be classified into different triangle types including: 

• isosceles acute triangles
• scalene acute triangles
• equilateral triangles

Other properties that help students recognise an acute triangle include the following:

• All three interior angles of an acute triangle have a sum of 180 degrees. 
• The angle opposite the longest side is the largest, and the angle opposite the smallest side is the smallest. 
• A line drawn from the triangle’s base to the opposite vertex is always perpendicular and measures the triangle’s height. 
• The perpendicular bisector forms a right angle within the acute triangle.
• Acute triangles have a circumcenter where the perpendicular bisector meets the triangle’s sides.
• The triangle’s base is perpendicular to the height. 

Examples of acute triangles

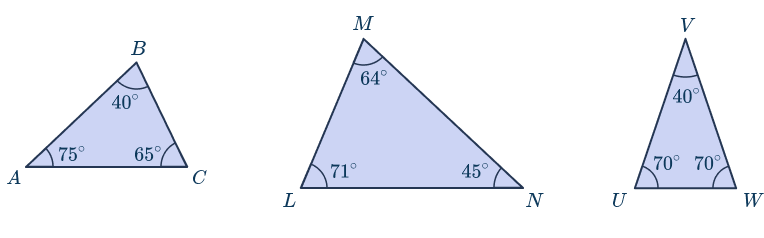
All three triangles above are acute triangles because they all have three acute angles. This means that each of the interior angles of the triangle is less than 90 degrees.

Types of acute triangles

We can classify triangles that are acute into three categories: an equilateral triangle, an acute isosceles triangle, and a scalene acute triangle. 

Here is the definition of each triangle type, their properties and an example.

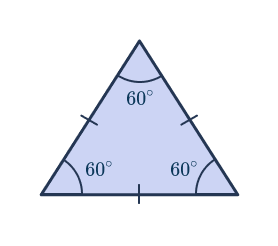
Equilateral triangle 

An equilateral triangle has 3 equal sides and 3 equal angles. All three angles each measure 60 degrees. 

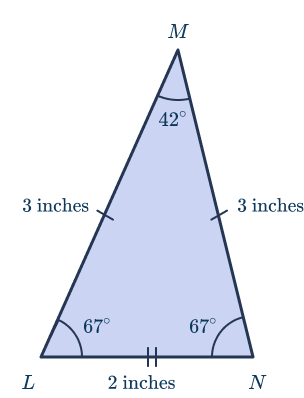
Isosceles triangle 

Acute isosceles triangles have 2 equal angles and 2 equal sides opposite of those angles. All three angles are less than 90 degrees each. The sum of the interior angles is 180 degrees.

Scalene triangle 

A scalene acute triangle has no equal sides, no equal angles and no lines of symmetry. All three sides have different lengths and all three interior angles of a triangle of this type are less than 90 degrees.

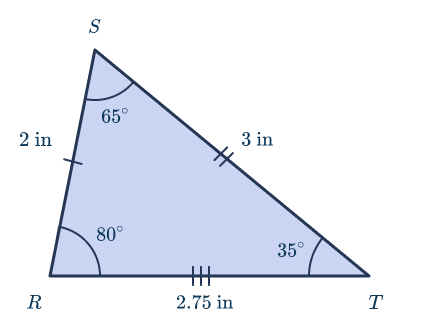
Relationships with other types of triangles

Acute triangles have some similarities and differences with other types of triangles. Right triangles have three angles, two are acute angles (less than 90 degrees). However, the third angle in a right triangle is a right angle, measuring at 90 degrees. 

Obtuse triangles also have three angles, with two acute angles measuring less than 90 degrees. But the third angle is an obtuse angle, an angle that is greater than 90 degrees. 

As an acute triangle shares properties with other triangles, it can transform into other types of triangles based on the lengths of its sides. For instance, an equilateral triangle has 3 acute, equal angles and 3 equal square unit sides. However, if two sides lengthen, it can create an acute isosceles triangle with 2 equal square unit sides and 3 acute angles with two angles being the same size. 

Lastly, if the triangle has 3 acute angles with no equal square unit sides, it becomes a scalene, acute triangle. 

Acute triangle formulas

To find the area of an acute triangle and the perimeter of an acute triangle, two formulas acute triangle formulas 

Here are both formulas, how to use them and some worked examples!

Area of an acute triangle

The area of an acute triangle refers to the amount of space the triangle occupies. To find the area of an acute triangle, students can use two formulas. 

The first formula is: A = \frac{1}{2} bh

In this formula: 

• A = area
• b = base
• h = height

The base of the triangle, b , is the side perpendicular to the height of the triangle. The triangle’s height is the length of a perpendicular line segment connecting the triangle’s base to its opposite vertex. 

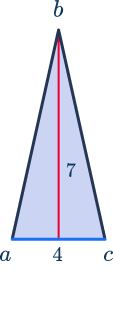
In the example above, triangle abc has a height of 7 square units and a base of 4 square units. 

Here’s how to use the formula to find the area of triangle abc :

\begin{aligned} A &= \frac{1}{2}bh \\\\ A &= \frac{1}{2}(4)(7) \\\\ A &= \frac{1}{2}(28) \\\\ A &= 14 \text{ square units} \end{aligned}

Heron’s formula is the second formula used to find the area of an acute triangle. 

A = \sqrt{s \, (s-a)(s-b)(s-c)}

In this formula: 

• A = area
• s = the semi-perimeter of a triangle
• a, b, and c are the lengths of the sides 

The semi-perimeter of a triangle can be found by adding all three sides together and dividing by 2.

s = \text{ semi-perimeter of a triangle } = \frac{a+b+c}{2}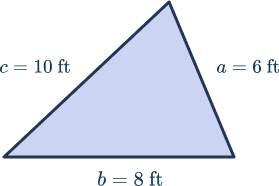

Here’s how to use Heron’s formula to find the area of the acute triangle above. 

First, find the semi-perimeter of the triangle: 

s = \text{ semi-perimeter of a triangle } = \frac{a+b+c}{2}

\begin{aligned} s &= \frac{6 +8 + 102}{2} \\\\ s &= \frac{24}{2} = 12 \text{ ft.} \end{aligned}

Knowing the semi-perimeter of the triangle is 12 ft., you can use Heron’s formula to find the area:

\begin{aligned} A &= \sqrt{s \, (s-a)(s-b)(s-c)} \\\\ A &= \sqrt{12 \, (12-6)(12-8)(12-10)} \\\\ A &= \sqrt{12 \, (6)(4)(2)} \\\\ A &= \sqrt{12 \, (48)} \\\\ A &= \sqrt{576} \\\\ A &= 24 \text{ ft.} \\\\ \end{aligned}

Perimeter of an acute triangle

The perimeter of an acute triangle is the sum of the length of its sides. Here’s the formula to find the perimeter:

P = \text{ perimeter of an acute triangle } = a+b+c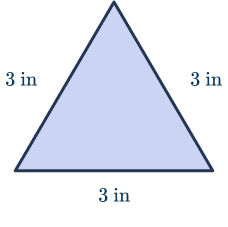

In the equilateral acute triangle above, each side has a length of 3 inches. Here’s how to the perimeter:

P = \text{ perimeter of an acute triangle } = a+b+c

\begin{aligned} P &= 3 \text{ in.} + 3 \text{ in.} + 3 \text{ in.} \\\\ P &= 9 \text{ in.} \end{aligned}

When do students learn about acute triangles?

Students learn to recognize shapes, including triangles, visually first as early as pre-kindergarten. in early elementary years, learners then move to a more descriptive way of thinking about shapes, such as discussing the basic properties of shapes. For example, triangles have 3 sides and 3 corners. 

By fourth grade, students begin to look at shapes analytically and characterize shapes by their properties. Students are introduced to acute triangles in fourth grade. As students’ mathematical journey progresses, they think about shapes abstractly. 

In middle school, students explore Heron’s formula and Pythagorean theorem. By 10th and 11th grade, students explore the world of trigonometry and the relationships between angles and side lengths of triangles. Learners for relationships between classes of triangles and other shapes which leads to higher-level geometry, including arguments and proofs.

Worked examples

Example 1: 4th grade 

What is the measure of angle DAC?

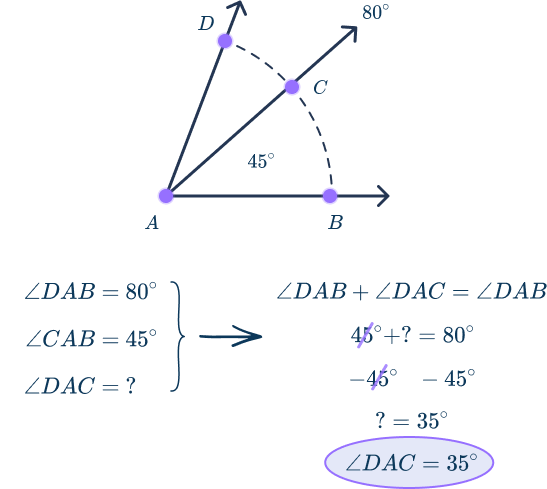
First, it’s important to recognize all three angles are acute angles. Angle DAB is 80 degrees and angle CAB is 45 degrees. 

To work out the measure of angle DAC , students must understand that two smaller angles can join together to create one bigger angle. Thus, they can add angle CAB to angle DAC to solve angle DAB . 

Using algebraic thinking, students can determine that the angle DAC = 35 degrees. 

Example 2: 4th grade

The sides of the triangle are 3 inches, 5 inches, and 2 inches. The sum of all three angles is 180 degrees. What kind of triangle is this?

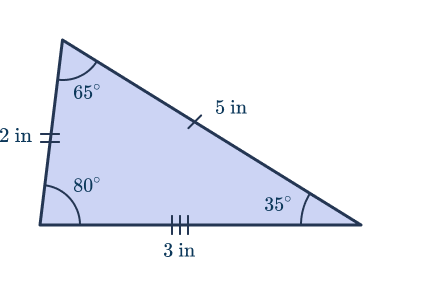
This is a scalene acute triangle, they have no equal sides and no equal angles. It’s acute because the sum of all three angles in the triangle is less than 180 degrees. 

Example 3: 6th grade 

What is the area of the triangle QRS ?

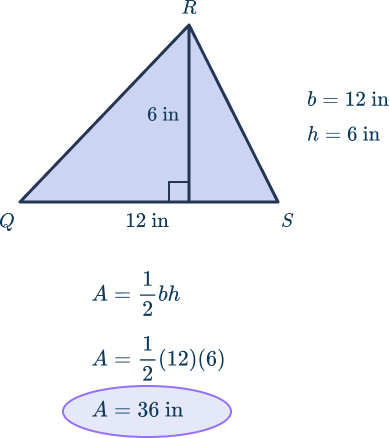
To find the area of a triangle like this, students should use the following formula: A= (\frac{1}{2})bh.  . 

QS is the base, which has a length of 12 inches. The triangle’s height is labeled 6 inches. Using the area of a triangle formula, students can determine that the area of triangle QRS  is 36 inches. 

12 x 6 = 72 

72 ÷ 2 = 36

Example 4: 6th and 7th grade 

For the triangle below, the perimeter is 80. Find the value of c . 

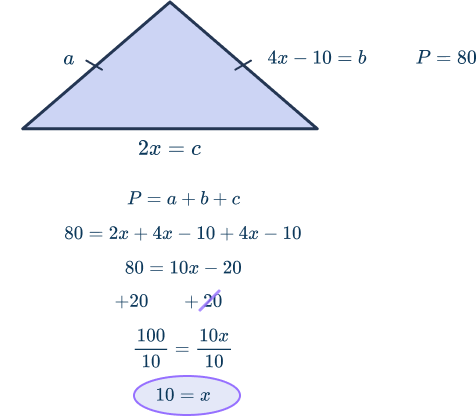
To find the perimeter of the triangle, students must use the formula: P = a + b+ c where a, b, , and c represent the sides of a triangle. 

Students know the perimeter of the triangle is 80 and the length of two sides: 4x-10 and 2x. . 

The dashes on two sides of the triangle mean those two sides are congruent, or equal. That means the length of the missing side is also 4x-10. . 

With the formula for each side, students can solve the perimeter using algebraic thinking: 

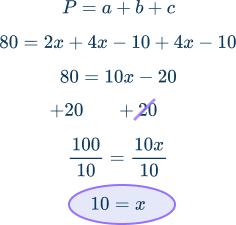
Knowing the value of x , students can find the value of c  

\begin{aligned} C &= 2x \\ C &= 2(10) \\ C &= 20 \text{ square units} \end{aligned}

Practice questions

Question 1: 4th grade 

Jenn drew an acute angle. Lenny drew an acute angle 3 times larger than Jenn’s. What is the largest possible angle Lenny could have drawn? Explain.

Question 2: 4th grade 

What is the measure of acute angle FGH? Explain how you know.

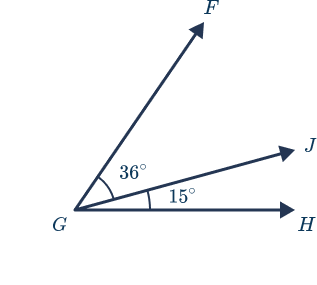
Acute angle FGH is made up of two smaller angles: angle FGJ and angle JGH. Two smaller angles can be joined together to create one bigger angle. Here is how students might solve  acute angle FGH:

\begin{aligned} \text{Angle FGH } &= \text{ Angle FGJ } + \text{ Angle JGH} \\ \text{Angle FGH } &= 36^{\circ} + 15^{\circ} \\ \text{Angle FGH } &= 51^{\circ} \end{aligned}

Question 3: 4th grade 

Find the missing acute angle.

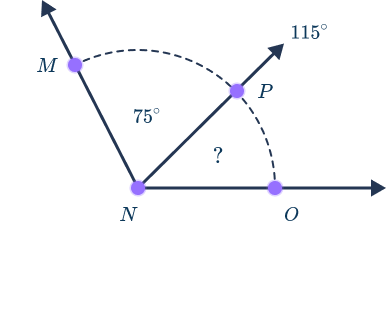
Acute angle PNO is the missing acute angle and is part of a larger angle, angle MNO. Two smaller angles can join together to create one bigger angle. Here is how students might solve acute angle PNO:

\text{Angle MNO } = \text{ Angle MNP } + \text{ Angle PNO}

\begin{aligned} 115^{\circ} &= 75^{\circ} + \text{ Angle PNO} \\ -75 \; & \; -75 \\ 40^{\circ} &= \text{ Angle PNO} \end{aligned}

Question 4: 6th – 8th grade 

What is the area and perimeter of the acute triangle TUV to the nearest tenth?

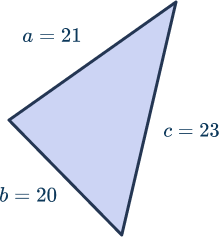
Students can use Heron’s formula to find the area of the triangle above. First, find the semi-perimeter of the triangle

s = \text{ semi-perimeter of a triangle } = \frac{a+b+c}{2}

\begin{aligned} s &= \frac{21+20+23}{2} \\\\ s &= \frac{64}{2} = 32 \text{ square units} \end{aligned}

Knowing the semi-perimeter of the triangle is 32 square units, learners can use Heron’s formula to find its area.

\begin{aligned} \text{Area of triangle TUV } &= \sqrt{s \, (s-a)(s-b)(s-c)} \\ \text{Area of triangle TUV } &= \sqrt{32 \, (32-21)(32-20)(32-23)} \\ \text{Area of triangle TUV } &= \sqrt{12 \,(11)(12)(9)} \\ \text{Area of triangle TUV } &= \sqrt{12 \, (1,188)} \\ \text{Area of triangle TUV } &= \sqrt{14,256)} \\ \text{Area of triangle TUV } &= 119.4 \text{ square units} \end{aligned}

The perimeter of an acute triangle is the sum of the length of its sides. 

Here’s how to find the perimeter of triangle TUV:

\begin{aligned} \text{P } = \text{ perimeter of an acute triangle } &= a+b+c \\ \text{Perimeter of triangle TUV } &= 21 + 20 + 23 \\ \text{Perimeter of triangle TUV } &= 64 \text{ square units} \end{aligned}

Why learn about acute triangles?

Learning about geometric shapes connects math to the physical world and supports mathematical thinking in subjects such as engineering and physical sciences. 

Acute triangles are one of the first shapes students study in fourth grade. Alongside acute angles that measure less than 90 degrees, acute angles have many properties that help to identify them. 

Students can use angle measures to find the area and perimeter of a triangle and later create arguments and proofs in trigonometry. 

The worked examples above can help to solidify and extend students’ knowledge of acute triangles.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?