What Is Area And Perimeter? Explained For Teachers And Students
Area and perimeter are real-world math concepts taught in elementary grades and expanded upon in middle school math. Children need to learn the definition of area and perimeter, the difference between the two and how to calculate area and perimeter for various shapes. Learning about area and perimeter helps students with real life skills outside of the classroom.
This guide focuses on the meaning of area and perimeter, examples of how to calculate the area and perimeter of various shapes and sample problems with worked explanations for area and perimeter at the elementary level.
What is the area and perimeter?
Area and perimeter are measurable attributes of two-dimensional shapes. Every 2D shape has an area and perimeter.
Area refers to the measure of the amount of space occupied by a flat math shape or non-math shape and is measured in square units. All two-dimensional shapes have a measurable area. If you lay a piece of paper flat on a table, the amount of space it takes up is the area.
Perimeter is the total distance around the boundary or outline of a two-dimensional shape and is measured in units. If you lay the same piece of paper on the table and trace a line around the outside of the paper, you are tracing the perimeter.
Area and perimeter real life examples
There are many examples of real world area problems. For example, if someone wanted to tile the bottom of a swimming pool they would need to know the area of the base of the pool. Or if they want to cover their yard with sod, they need to measure the area of their yard.
There are also many examples of area in a classroom, such as the area of the surface of a desk, the area of the board in the front of the classroom, and the area of the classroom rug.
Perimeter is different from the area. Knowing how to measure the perimeter of a shape is a helpful life skill in situations such as knowing how much fencing you need to fence in a yard.
Another example is calculating the distance around a running track or measuring the distance around the outside of a picture frame.
A useful way to describe perimeter to young learners is to imagine you had a picnic blanket on the ground and an ant walked around the outside of the picnic blanket, it walked the perimeter of the blanket.
Perimeter Check for Understanding
10 questions with answers covering a range of 3rd and 4th grade perimeter topics.
Download Free Now!When do students learn about areas and perimeter?
Children learn about area and perimeter in a spiral curriculum throughout elementary school in the Measurement & Data and Geometry domains of common core standards. First, students must learn basic measurement units and skills in the lower elementary grades.
In 3rd grade math, children learn about the meaning of area and relate it to multiplication. In 4th grade, students learn how to calculate the area of rectangles and the perimeter of rectangles. By the end of 5th grade, children should apply area and perimeter to find volume of three-dimensional shapes.
Beyond 5th grade, students learn formulas to calculate the area of triangles in 6th grade, the area of circles in 7th grade and later the volume of a variety of three-dimensional figures in 8th grade.
Area and perimeter content learned at each grade level
| Grade Level | Area/Perimeter Topics Learned |
| 2nd Grade | Pre-Area/Perimeter Concepts:
|
| 3rd Grade | Understand concepts of area and relate area to multiplication and addition
|
| 4th Grade | Apply the area and perimeter formulas for rectangles in real-world and mathematical problems |
| 5th Grade | Expand on understanding of two-dimensional area to calculate volume of three-dimensional figures
|
| 6th Grade | Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing them into rectangles or decomposing them into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.Find the volume of right rectangular prisms with fractional side lengths |
| 7th Grade | Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms. |
| 8th Grade | Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems. |
Calculating area and perimeter
Calculating area and perimeter ranges in difficulty. It’s fairly straightforward to calculate the area and perimeter of regular polygons but irregular polygons and irregular shapes are more challenging.
How to find the area of a shape
When students first learn to find area, they begin with finding area of rectangles and squares. An effective teaching strategy is to connect the area of rectangles and squares to multiplication.
Students then advance to finding the area of other shapes such as triangles and squares. In 6th grade, learners begin to find the area of more difficult polygons and geometric shapes.
Here are the formulas for calculating the area of different shapes commonly seen in elementary and middle school.
Area of a rectangle
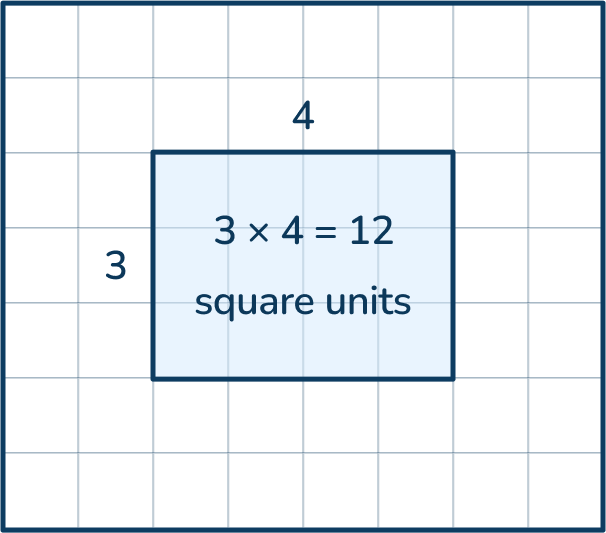
To calculate the area of a rectangle, students need to multiply the shapes length by the width.
length x width
- First, measure the length and width of the rectangle.
- Multiply the two dimensions together to find the area.
A helpful visual model for finding area is to use grid paper so students can see how the area fills the space inside the rectangle. Learners can also use the grid squares to prove the concept of area and check their work when calculating. When using grid squares, the area is measured in square units.
Area of a square
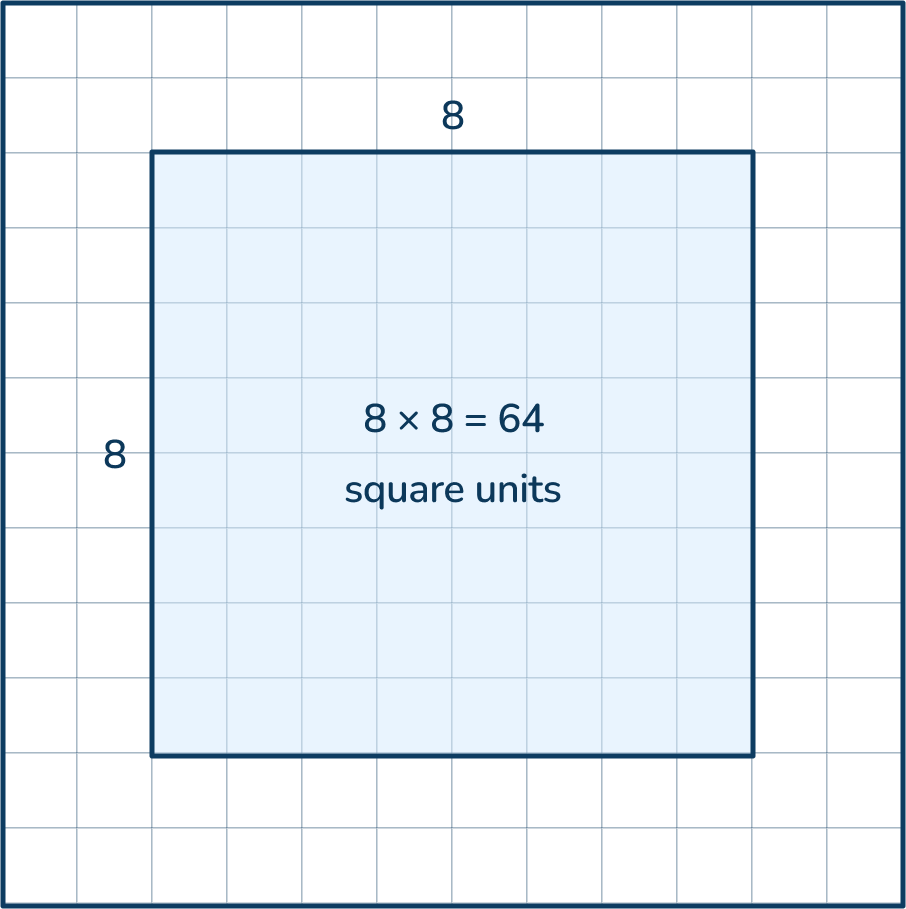
Finding the area of a square is similar to finding the area of a rectangle. The sides are multiplied together. The difference is the side lengths of a square are the same length so you can multiply the measure of one side length by itself.
To calculate the area of the square, learners must measure the side of the square and multiply it by two.
It can be written as:
- side length x side length
- side length x 2
- side length squared or side length ²
For example, if the length of the side of a square is 8 feet, the area is calculated by finding 8².
When students first learn to find the area of rectangles and squares in third grade they have not yet learned about exponents. Using the formula side length x side length is more appropriate than side length².
However, at the upper elementary level in fourth and fifth grade, teachers can introduce the exponent method.
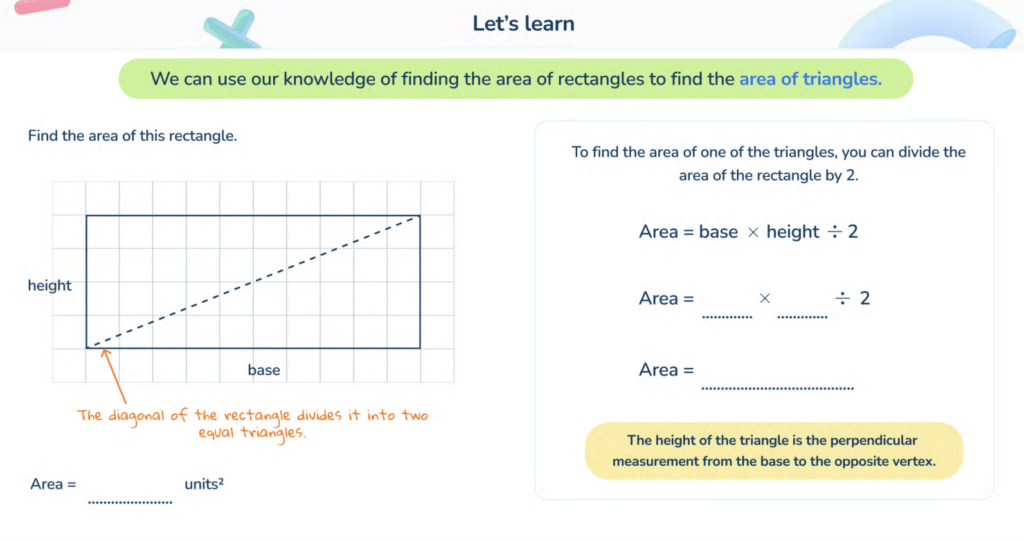
Area of a triangle
Students find the area of an equilateral triangle and other types of triangles in 6th grade and beyond.
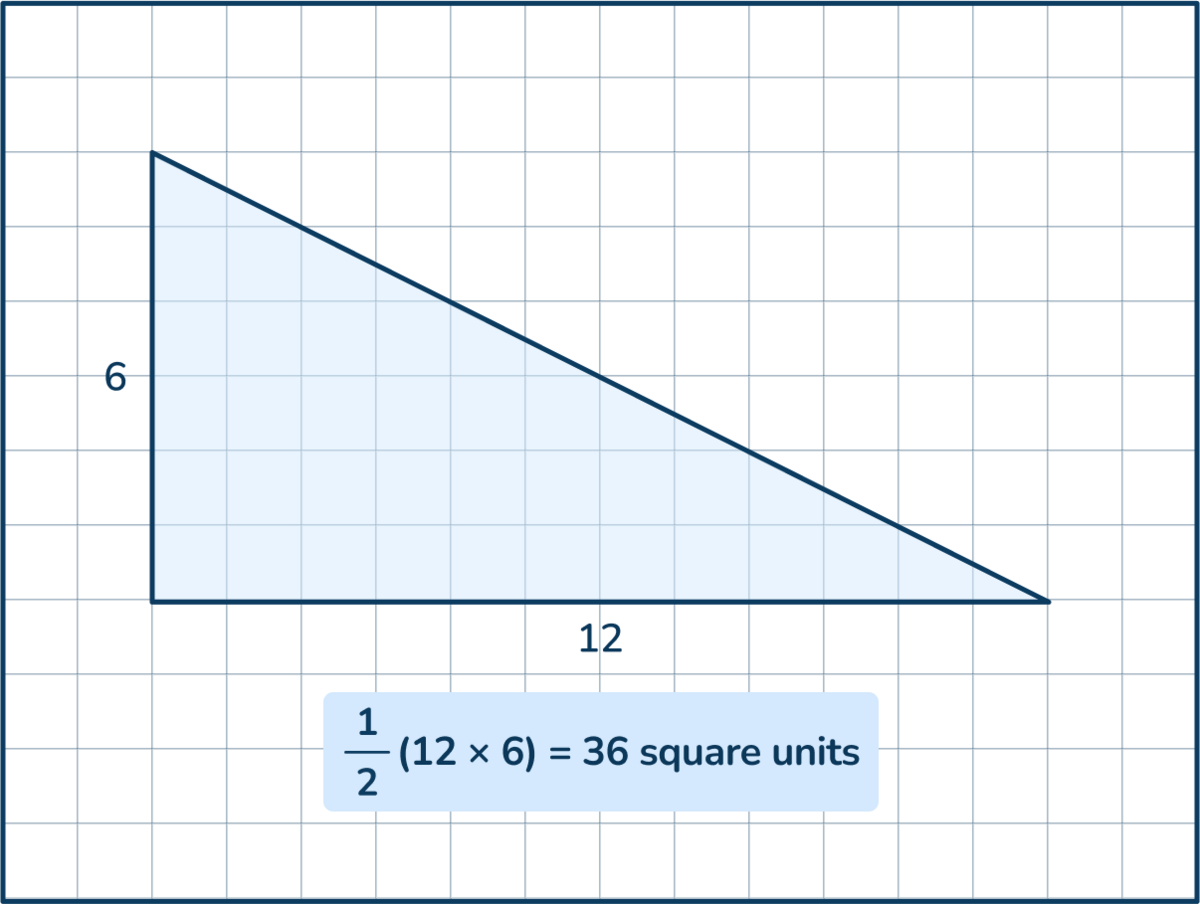
The formula for calculating the area of a triangle is \frac{1}{2}bh. This means students need to calculate \frac{1}{2} of the base x the height. Students can also write this formula as \frac{base x height}{2}.
To find these measurements, students need to:
- measure the length of the triangle base;
- measure the height from the base to the top point of the triangle;
- multiply the two numbers together;
- halve the total or divide the total by two.
Area of a circle
In 7th and 8th grade students learn to calculate the area of a circle.
To find the area of a circle, students must first find the radius by measuring from the midpoint of a circle out to any point along the circle border.
They can then use the formula for calculating the area of a circle, πr². Which can also be written as π x r x r.
Summary table of formulas for area
Area Formulas for Polygons at the Elementary Level
| Shape | Formula for Calculating Area(Square Units) |
| Rectangle | Length x width |
| Square | Side length x side length or side length² |
| Circle | \frac{1}{2}bh or \frac{base x height}{2} |
| Triangle | πr² or π x r x r |
Units of measurement for area
Area is always recorded in square units. These can be either US-Standard or metric square units. The specific units differ based on the size of the shape and the reason for measuring area.
For example, a large shape such as a football field might have an area recorded in square yards, where yards is the unit chosen. But to find the area of a piece of paper, square inches is a more appropriate unit.
Teachers can help students determine an appropriate unit of measure by considering the linear measurement of one side of the shape.
For example, when measuring the area of a wall for wallpaper, measuring the length of one wall in feet is an appropriate unit of measure. Therefore, the measure of the area of the wall would be in square feet.
Area can be converted to different unit squares. To do so, students need to:
- convert both dimensions to the new unit;
- calculate the area.
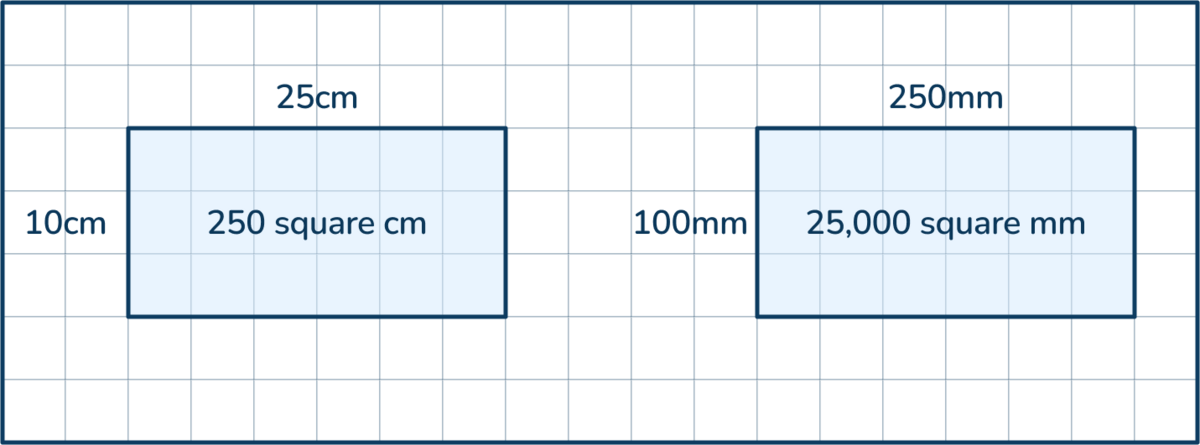
For example, if the length of a rectangle is 25 centimeters and the width is 10 centimeters, the area is 250 square centimeters.
25cm x 10cm = 250cm²
To find the area in square millimeters unit of measure:
- convert the 25cm length to millimeters by multiplying by 10 because there are 10mm in one cm;
- convert 10cm to mm by multiplying by 10;
- calculate the area.
25cm x 10 = 250mm
10cm x 10 = 100mm
250mm x 100mm = 25,000mm²
This concept can be confusing for students. They may be tempted to multiply the area in centimeters (250 square centimeters) to millimeters by multiplying 250 x 10. However, this does not represent the new unit of measurement correctly.
Drawing visual models and using physical objects can help children understand this concept.
How to find the perimeter of a shape
Students first learn how to find perimeter by finding linear measurements and connecting that skill to calculating perimeter.
Like area, students begin by finding the perimeter of rectangles, squares and other parallelograms in 3rd, 4th and 5th grade and then transition to finding the perimeter of circles, triangles and harder polygons in 6th and 7th grade.
Perimeter is the sum of the lengths. For basic geometric shapes like triangles, rectangles, trapezoids and parallelograms a formula is not needed. But learning the formulas can be helpful and make calculating the perimeter more efficient.
The following formulas for calculating the perimeter of various polygons are commonly seen at the elementary and middle school level.
Perimeter of a rectangle
The goal of calculating the perimeter of a rectangle is to efficiently add together the length of all four sides. For this, students can either calculate:
- length + length + width + width
or
- (length + width) x 2
Real life examples of perimeter of a rectangle include:
- Fencing around a rectangular yard;
- Tiling around the outside of a rectangular swimming pool;
- Taping the perimeter of a wall;
- Sewing ribbon around the outside of a rectangular blanket;
- Walking around the outside of a rectangular block.
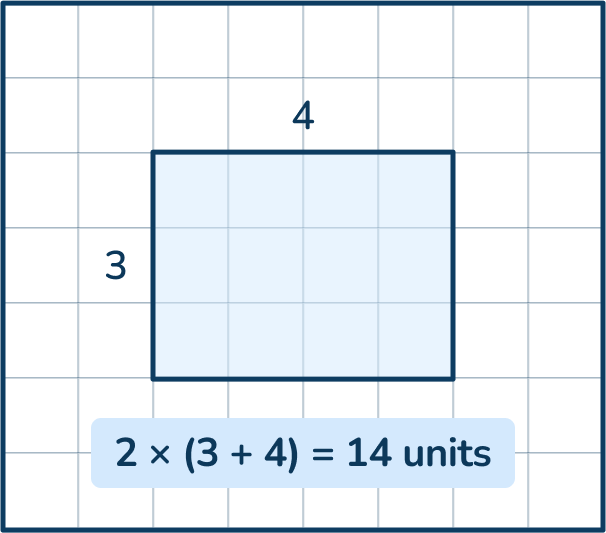
Perimeter of a square
The formula for calculating the perimeter of the square is either:
- side length + side length + side length + side length
or
- 4 x side length
As squares have four equal sides of the same length, the perimeter can be calculated efficiently by multiplying the length of one side by the total number of sides, which is four.
Real world examples of perimeters of squares are the same as rectangles, but squares have four sides of the same length.
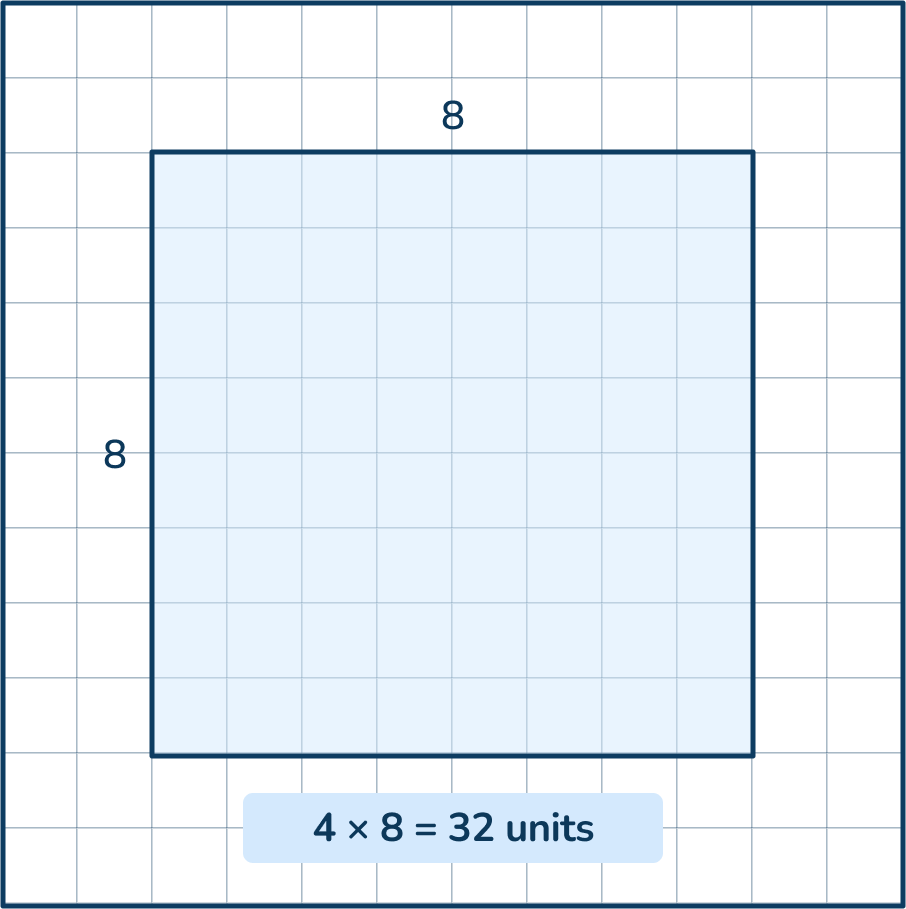
Perimeter of a circle
In 7th grade, students learn to calculate the perimeter of a circle, also known as the circumference. The circumference is the total distance around the outside of a circle.
Calculating the perimeter of a circle is more complex than calculating the perimeter of other polygons because the sides are curved and there are not easily distinguishable side lengths.
To calculate the perimeter of a circle students can use two formulas:
- 2 x π x radius
or
- 2πr
Perimeter of a triangle
Students learn to find the perimeter of a triangle in sixth grade. The formula is not as complex as the formula for area of a triangle.
Since the meaning of perimeter is the sum of all side lengths, the formula for finding perimeter of a triangle is simply a + b + c, where a,b, and c represent the three side lengths of the triangle.
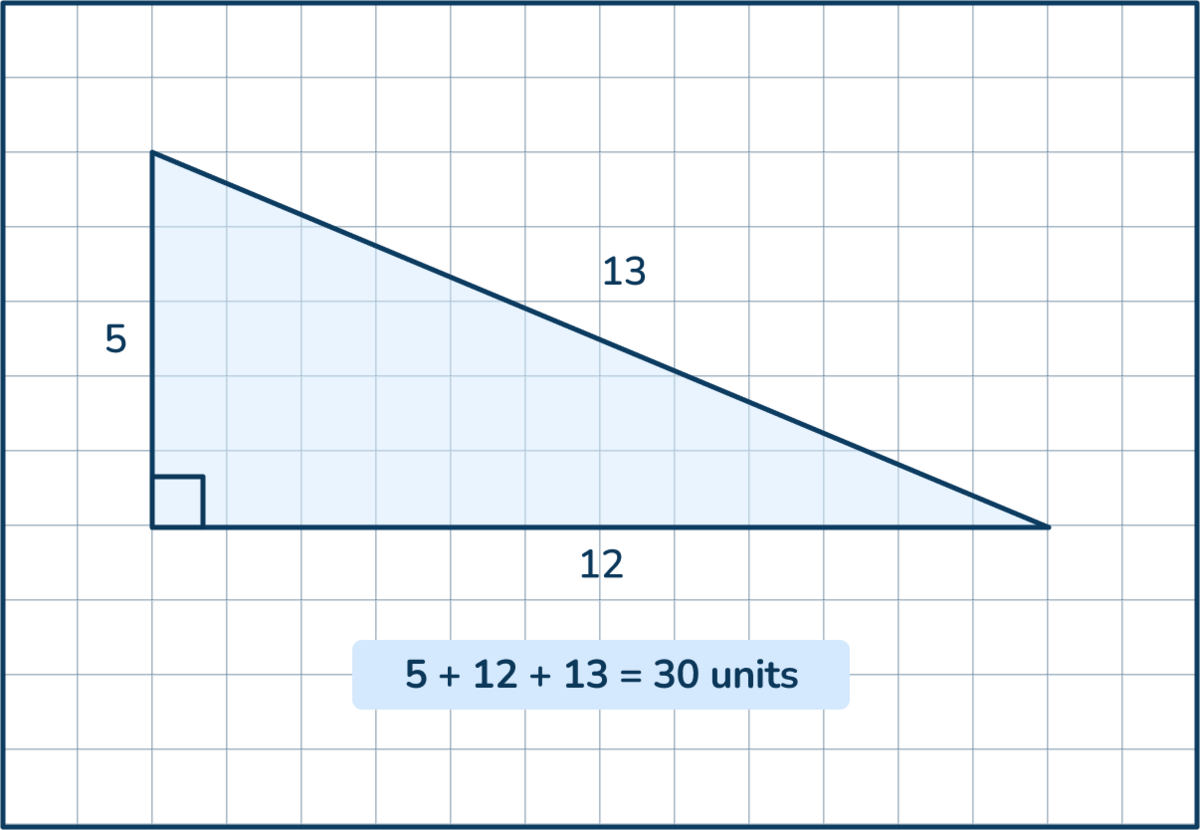
Perimeter Formulas for Polygons at the Elementary Level
| Shape | Formula for Calculating Perimeter (Units) |
| Rectangle | 2(l + w) or l + l + w + w |
| Square | 4 x side length, or l + l + l + l |
| Circle | Perimeter of a circle is known as circumference. The formula for calculating circumference is:2πr(or 2 x π x radius) |
| Triangle | a+b+c (add all three side lengths together) |
Units of measurement for perimeter
Perimeter is always recorded in linear units. These can be either US-Standard or metric units. The specific units differ based on the size of the shape and the reason for measuring perimeter.
For example, the perimeter of a large shape such as the fence around a yard might be measured in yards or feet, while the perimeter of a desk might be measured in smaller units such as inches.
To determine an appropriate unit of measure, first consider the linear measurement of one side of the shape and which unit would be most appropriate.
For example, if measuring the perimeter of a rectangular swimming pool, measuring the length of one side of the pool in yards is appropriate. The measure of the perimeter would be in yards.
To convert perimeter measurement to a different unit, such as feet to inches, convert the entire perimeter using the appropriate conversion rate.
For example, converting a room with a perimeter of 36 feet to inches.
There are 12 inches in one foot so students must multiply the perimeter by 12.
36ft x 12 = 432 inches
The answer would be the same if you multiply each dimension by 12 to convert each dimension from feet to inches and then calculate the perimeter.
- 8ft x 12 = 96 inches
- 8ft x 12 = 96 inches
- 10ft x 12 = 120 inches
- 10ft x 12 = 120 inches
- 120 + 120 + 96 + 96 = 432 inches
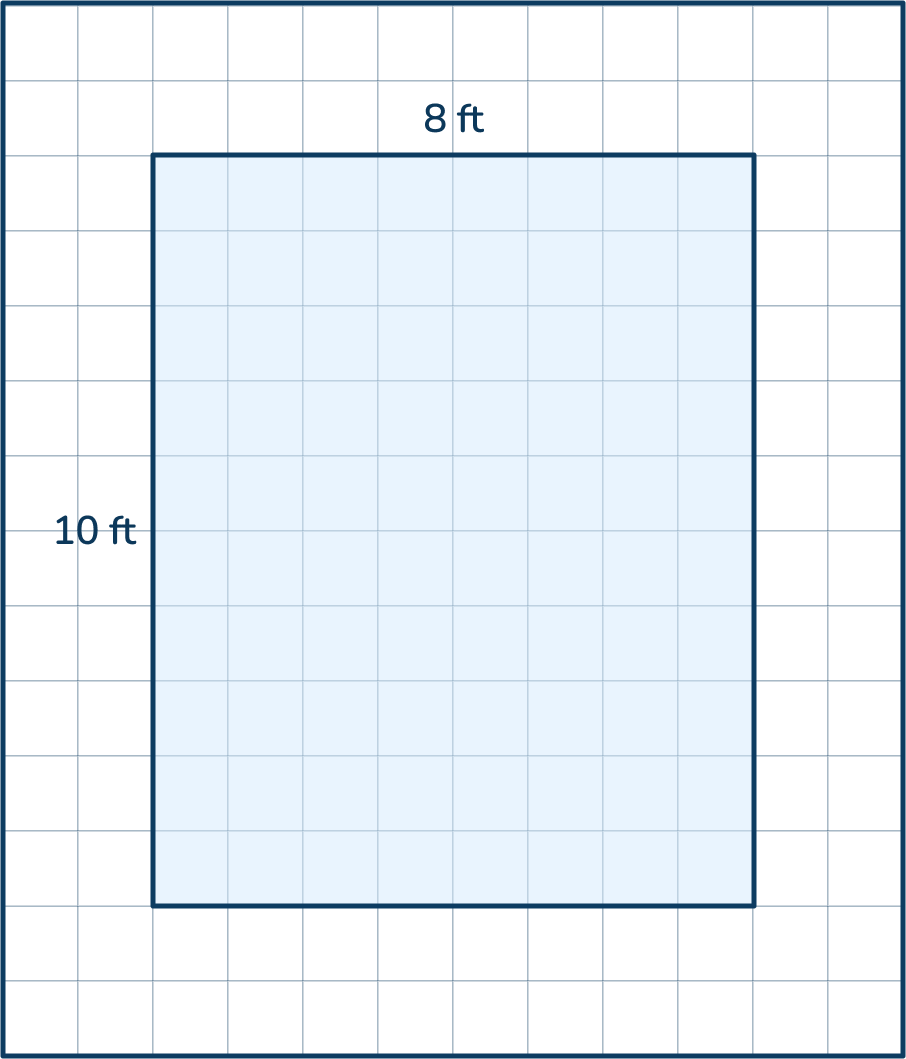
The relationship between area and perimeter
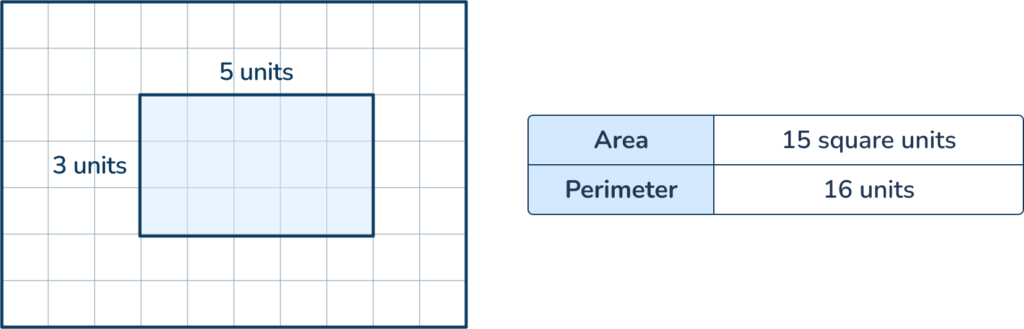
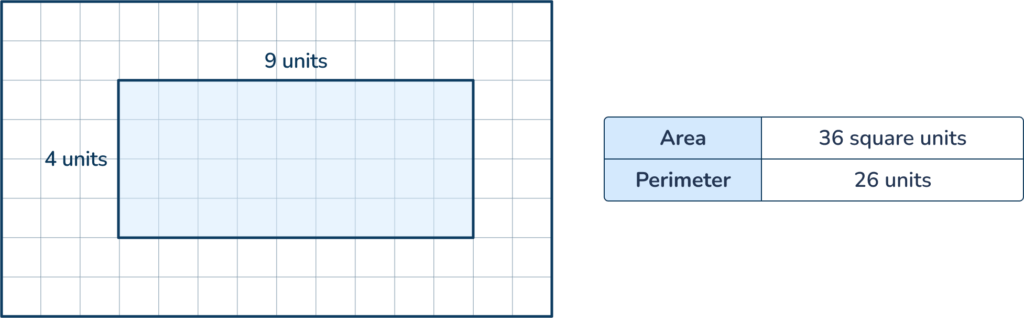
Area and perimeter are related measurements. Both area and perimeter involve the measure of side lengths of a shape. In some cases, the number measurement of the area may be larger than the perimeter and vice versa.
However, it is important to remember that the measurement units used for area and perimeter are different. Area is measured in square units while perimeter is measured in linear units.
When calculating area and perimeter remember there is no direct relationship between the two aside from using the side lengths as part of the formula.
Teachers should always encourage students to build a conceptual understanding of area and perimeter before applying the formulas for calculating these measurements. This will help prevent misunderstandings about which measurements to use and why.
The examples below show the area measures larger than the perimeter, and the reverse.
Area and perimeter worked examples
These perimeter and area worked examples reflect what 3rd grade – 5th grade students might see on perimeter or area worksheets or assessments.
Each example includes step-by-step instructions for problem solving.
Third Grade
Calculate the area of the rectangle below. Record your answer in square units.
Answer: 32 square units
- Step 1: Determine the length and width of the rectangle in square units. Length =8 units and width = 4 units. You may need to use a measuring tool or square units provided.
- Step 2: Calculate the area using the formula length x width. 8 units x 4 units.
- Step 3: Record the answer in square units. 32 square units.
Fourth Grade
The length of the rectangle below is 9 feet and the area is 54 square feet. What is the perimeter of the rectangle?
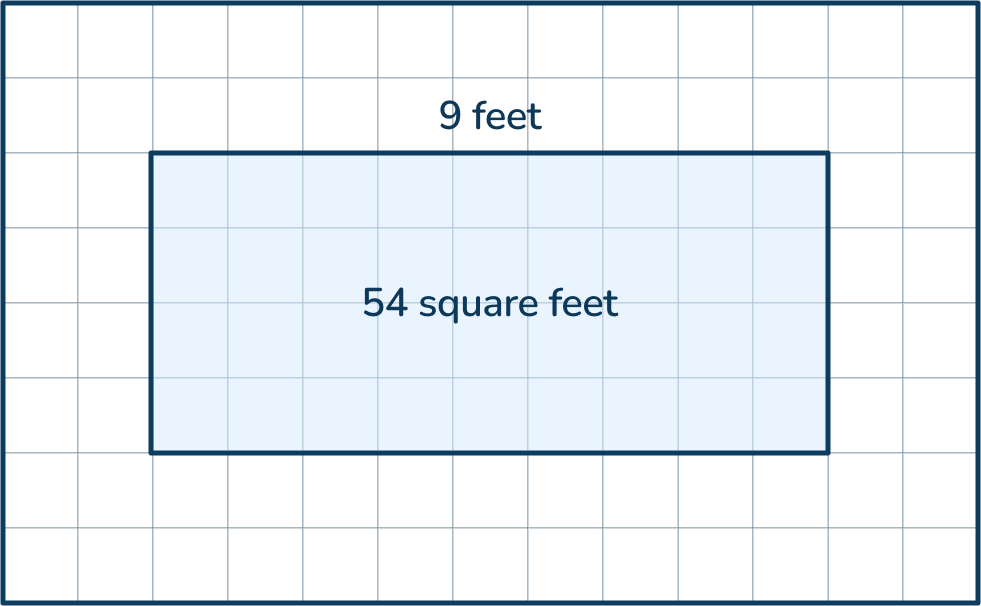
Answer: the perimeter is 30 feet
- Step 1: Determine the rectangle width, and divide the area by the length. If students know the formula for calculating area is a = l x w, they can use the inverse operation to determine one side length, w = a ÷ l.
- Step 2: Determine the perimeter using the formula (l x w) x 2. (9 + 6) x 2 = 30 feet.
Fifth Grade
Find the area of the rectangle below in square feet.
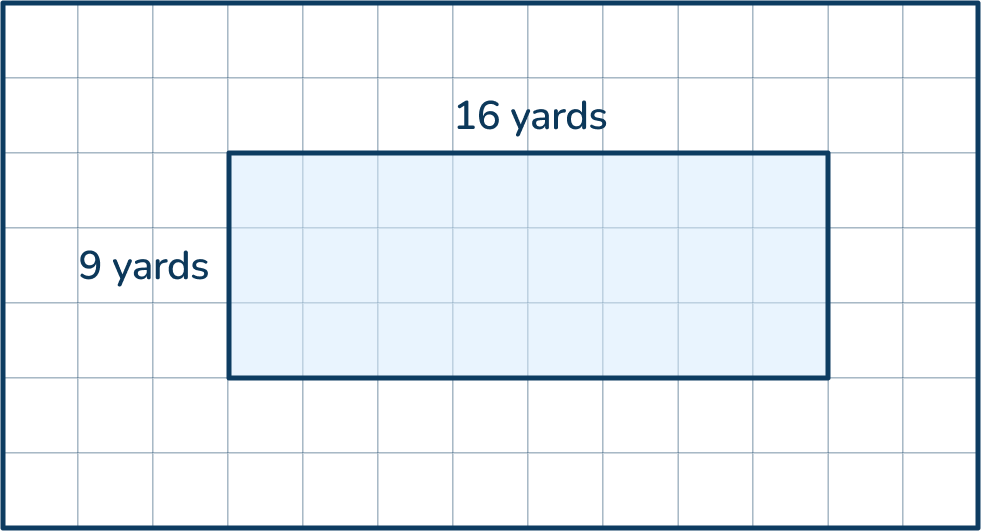
Answer: 1,296 square feet
- Step 1: Convert the length and width to feet. There are 3 feet in one yard so each dimension needs to be multiplied by 3. 16 yards x 3 = 48 feet. 9 yards x 3 = 27 feet.
- Step 2:Calculate the area in square feet. 48 x 27 = 1,296 feet.
Area and perimeter practice word problems
These word problems are typical of what students see on area and perimeter worksheets in the Geometry & Measurement and Data domains. The complexity of each word problem progresses from 3rd Grade through 7th Grade math.
Each problem includes a grade level alignment as well as an answer.
3rd grade word problems
A designer measured a wall she wanted to paint. The wall is 8 feet long and 6 feet tall. What is the area of the wall in square feet?
Answer: 48 square feet
4th grade word problems
The area of the garden is 72 square feet. But the gardener only has 50 feet of fencing for the garden perimeter.
What are all the possible dimensions for the garden? Remember it must have an area of 72 square feet and a perimeter of less than 50 feet.
Answer:
8 feet x 9 feet
Perimeter 34 feet
6 feet x 12 feet
Perimeter 36 feet
4 feet x 18 feet
Perimeter 44 feet
5th grade word problems
A moving box is 22 inches tall and has a base with an area of 240 square inches. If the length of the box is 16 inches, what is the perimeter of the base of the box?
Answer: 62 feet.
First divide 240 by 16 to get the width which is 15. Then calculate the perimeter.
6th grade word problems
A farmer wants to put fresh soil in a triangular patch of their farm. The triangle base is 15 yards and the height is 6 yards.
How many square yards of soil will the farmer need to buy to fill the triangular patch of land?
Answer: 45 square yards
\frac{1}{2} (15 x 6) = 45 square yards of soil
7th grade word problems
The bakery made a large circular pie with a radius of 9 inches. What is the circumference of the pie?
Answer: 56.52 inches
2π(9) = 56.2 inches
For over 10 years, Third Space Learning has provided one-on-one math sessions to the students who need it most. Specialist math tutors work with students on the math skills and concepts they need help with.
Sessions cover the full range of standards, including Geometry. Tutors personalize lessons and work at a pace and pitch to suit the student.
Area and perimeter FAQs
Area = length x width of a regular polygon
Perimeter = length + length + length + length of a regular polygon
Every shape has an area formula. The following is a list of formulas for calculating the area of common shapes:
Rectangle = length x width
Square = side length x side length
Triangle = /frac{1}{2}[katex} base x height
Circle = π radius²
Every shape has a formula for calculating perimeter. The following is a list of formulas for calculating perimeter of common shapes:
Rectangle = 2(l + w) or l + l + w + w
Square = 4 x side length, or l + l + l + l
Circle = Perimeter of a circle is known as circumference. The formula for calculating circumference is = 2πr (or 2 x π x radius)
Triangle = a+b+c
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state's standards and assessments, plus you'll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
- 2nd grade tutoring
- 3rd grade tutoring
- 4th grade tutoring
- 5th grade tutoring
- 6th grade tutoring
- 7th grade tutoring
- 8th grade tutoring
Why not learn more about how it works?
