How To Teach Math: 10 Effective Strategies For Teaching Math In The Classroom

Strategies for teaching math are ever-evolving. I see the phrase ‘teaching for understanding’ quite a lot, and it always confuses me slightly.

For knowledge and skills gained in the math classroom to persist beyond high school (and be useful in the future), an effective math education is essential. It ensures students have a deep understanding of the concepts involved beyond simply replicating a method on an exam.

Obviously, within the current education system, there are constraints and external pressures to take into account.

Here, I take you through 9 key teaching strategies for introducing new concepts. These will enhance student understanding while increasing their ability to learn math so that the knowledge and skills gained persist beyond the next assessment!

While this article will focus on classroom practice and planning learning cycles to help students understand new concepts, these principles also apply to independent learning and revision.

Look out for the ‘Top Tip‘ in each section to help teach math effectively to your students.

Let’s dive into the 9 essential takeaways for teachers and students to follow together, whatever stage they’re at on their math learning journey.

1. Create an engaging math class environment

Creating an engaging math class encourages student motivation and interest in math. A well-designed classroom environment can promote active learning, encourage student participation, and make math lessons more enjoyable. Here are some strategies for creating an engaging math class environment:

• Use visual aids and manipulatives: Visual aids like charts, graphs, and manipulatives such as blocks and tiles can make abstract mathematical concepts more tangible and easier to understand. For instance, using fraction tiles can help students visualize and grasp the concept of fraction addition.

• Incorporate technology: Utilize math software and apps to provide interactive and engaging math lessons. Tools like interactive whiteboards and online math games can make learning math fun and interactive, helping to keep students engaged.

• Encourage student collaboration: Group work and peer-to-peer teaching can foster a collaborative learning environment. When students work together to solve problems, they can learn from each other and develop a deeper understanding of math concepts.

• Use real-world examples: Relating math lessons to real-world scenarios can make math more relevant and interesting to students. For example, using examples like calculating discounts during shopping or measuring ingredients for a recipe can help students see the practical applications of math.

• Provide hands-on activities: Hands-on activities and projects allow students to explore and discover mathematical concepts on their own. Activities like building geometric shapes or conducting surveys and analyzing data can make math lessons more engaging and interactive.

By creating an engaging math class environment, teachers can help students develop a positive attitude towards math and improve their math achievement.

2. Check for prior knowledge when learning new math

Mathematics is a hierarchical subject, in that understanding new concepts depends on other underlying fundamental concepts. For example, to understand how multiplication works, students need to have a well-developed concept of addition to understand the concept of repeated addition and the links to multiplication.

The more complex the math level, the more foundational understanding blocks are needed. For example, fraction addition requires an understanding of:

• What a fraction is and what it represents;

• Equivalent fractions;

• Improper fractions and mixed numbers;

• General integer multiplication and number sense;

• Identifying multiples, including the lowest common multiples.

If one of these underlying concepts is underdeveloped (or missing), learners struggle far more to assimilate the new concept of fraction arithmetic with their existing knowledge. They are attempting to build the new concept up on wobbly foundations.

If misconceptions exist in the foundation blocks, it is likely that these misconceptions will compound as students attempt to understand new concepts.

By the time students reach middle school and high school level, there are many more of these interlinked concepts and many more opportunities for baked-in misconceptions.

Clearly, there is not enough syllabus time to re-teach every math topic from scratch, as if students have never experienced it before. We need to find a happy medium that allows our students to explore their prior math skills and knowledge and highlight issues.

3. Assess a starting point to establish realistic next steps

When beginning a new unit of work or topic, give students a quick, low-stakes diagnostic assessment. This will help engage students, assess their prior knowledge and work out a starting point.

Fraction addition example: establishing misconceptions

Taking my example of fraction addition, I might give students a few questions targeting some of the concepts I want to teach.

This does not have to be a written assessment. A mini-whiteboard quiz is just as valuable and is often a better way to get glimpses of general patterns.

If I was planning a unit on fraction addition, I’d be looking for things like:

• Can students use bar modeling or diagrams?

• Are students using a standard algorithm?

• If they are, is it correct?

• Are there basic arithmetic errors? Do students need work on multiplication facts recall? 

• Can students simplify answers correctly?

• Can they tackle mixed number problems using their preferred method – are there issues with improper and mixed number conversion that need to be tackled first?

Before teaching any new content, go back and address any large-scale misconceptions.

In some circumstances, it may be more appropriate to target individual students or small groups with a brief intervention. For example, direct them to a personalized learning program or video tutorials to review the key concepts.

Third Space Learning’s one-on-one, online math tutoring uses ongoing assessment to gauge students’ understanding and identify learning gaps. Using this information, tutors personalize teaching to address each student’s needs.

With lots of curriculum content to get through, it’s difficult to feel confident spending lesson time reviewing content they ‘should already know’, rather than giving new math instruction.

However, ensuring that new concepts are built on more solid foundations using a spiral curriculum has two big advantages.

1. The new concept is learned more quickly, as students can slot the new ideas into a clear existing framework;

2. If students build a conceptual understanding of new math, it is more likely to move from the student’s short-term to long-term memory. This means that less re-teaching will be needed in the future.

---

4. Work within the constraints of working memory

Research from cognitive science suggests that direct math instruction is generally more effective than discovery-based learning (Kirschner, Sweller and Clark 2006).

Be aware of cognitive overload and the relationships between working memory and long-term learning and memory, and how these impact students’ mathematical thinking.

Fraction addition example: comparing working memory

Returning again to adding fractions, let’s look at two different students.

Student A

Student B

They understood equivalent fractions when it was taught the first time around.They have a good concept of multiples.They have good times table recall.They have a good understanding of the underlying mathematical concepts.The procedures for calculating equivalent fractions and simplifying fractions are well-organized in their long-term memory.The relevant multiplication facts are there for rapid recall when needed.When they listen to an explanation on fraction addition, their working memory can concentrate fully on the new bits; why a common denominator is important and how to actually add the two fractions.

They can’t really remember what an equivalent fraction is (and probably didn’t really understand it in the first place).They were absent when multiples were taught.They aren’t particularly secure with 6, 7 or 8 times tables.They have a lot more going on in their working memory.– How has 45 \frac{4}{5} suddenly become 2430 \frac{24}{30} ?– What’s 4 × 6? 6, 12, 18, …– How does the teacher just ‘know’ what the denominator is? Why are they talking about multiples?

Student B is disadvantaged from the start. They aren’t secure woth the basic math they need to solve the problem. This creates extra work and cognitive overload. Therefore, Student B will progress slower than Student A.

The gaps in foundational mathematical knowledge must be addressed before introducing new concepts. If this is not possible (due to curriculum design or time constraints), we could support Student B and reduce their cognitive load. For example, we could provide them with a multiplication chart.

This is a hugely oversimplified model, and I don’t pretend to be a cognitive science expert.

However, we’ve all seen this in the classroom where students struggle to grasp a new concept. It isn’t because the new concept itself is particularly difficult, but because their brains are struggling making connections due to lacking the fundamental concepts.

---

5. Develop mathematical understanding using models

It can be very useful for students to use models or frameworks to link to the new information.

Visualizing math content through modeling

Manipulatives and models are useful in math at all grade levels. I particularly like bar modeling and algebra tiles for visual representations of a mathematical scenario. There are some great interactive versions available online.

These models are not generally the end goal. But, they can be an appropriate stopping point for some students and are valid methods for solving problems at high school level.

There is sometimes a temptation to cut out modeling for older students, skim over the understanding, and go straight to using an algorithm.

However, if you introduce students to a step-by-step procedure without the underlying conceptual ideas, they will be less successful when applying these procedures to non-standard problems. They’ll also struggle to recall the steps when they are needed further down the line.

Fraction addition example: modeling ideas

If there are underlying misconceptions about how fractions work, go back to basics. Use partitioned bars to illustrate examples of equivalent fractions.

Ensure students can find equivalent fractions, then build up to adding like fractions, and finally, unlike fractions.

Another way to explore links is to consider multiple representations of the same topic.

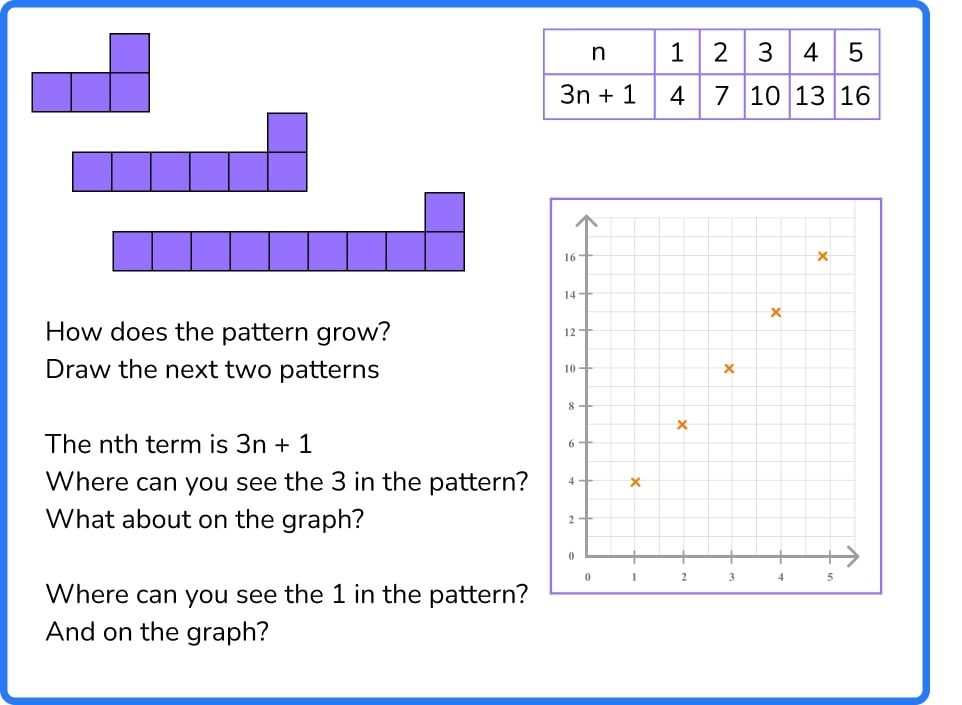
For example, I’ve used Jo Boaler’s suggestions for multiple representations of sequences to explore the links between sequences, functions and graphs. This kind of material is great for encouraging students to mathematical reasoning.

---

6. Develop familiarity with manipulatives and models

To illustrate this, I used algebra tiles when trying to find a way to explain to a group of 9th graders why we half the coefficient of x when completing the square.

I’d attempted to teach the process algorithmically, which had completely confused the majority of the class. I realized that I was asking them to do something far too abstract on some pretty shaky foundations.

Following a bit of research, I returned to them with some algebra tiles I’d cut out of cardboard.

We physically moved the x tiles around to convert the rectangular areas into squares. Some students suddenly understood why it was called ‘completing the square’!

After a couple of lessons on this, most of them were completing practice problems fairly competently.

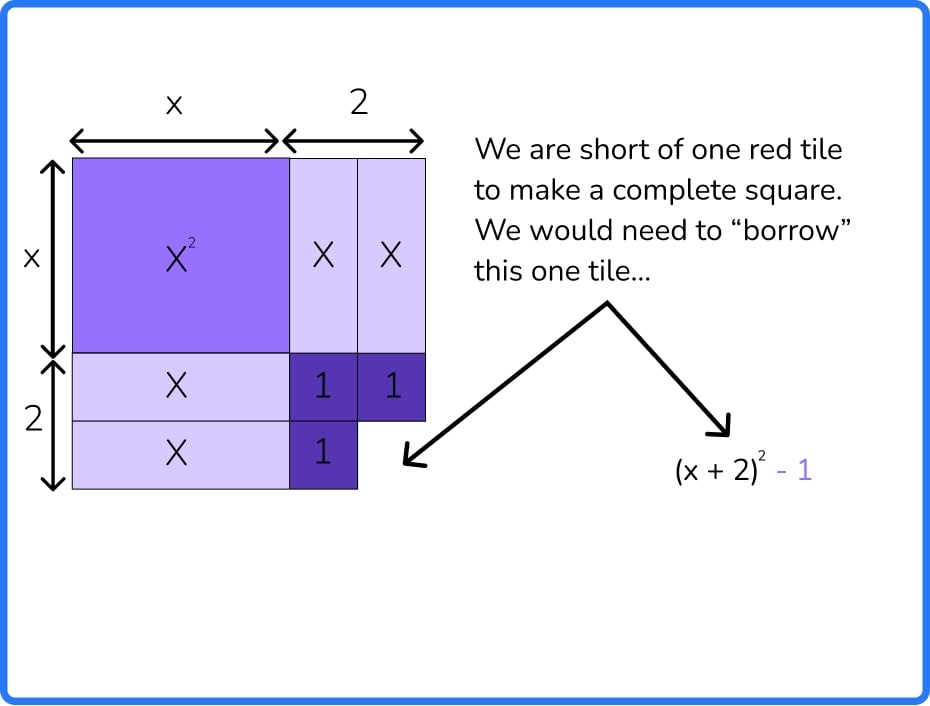
However, we had quite a few hang-ups on getting to grips with how the tiles worked; I was simultaneously asking every student to become familiar with a new visual representation of algebra, while also asking them to understand quite a complex new concept.

In subsequent years, most of my classes saw algebra tiles long before I asked them to complete the square with them, and this problem was significantly reduced.

Using models in this way can also help English language learners understand more abstract math concepts.

7. Connect math to the real-world

I don’t really like the phrase ‘real-world math’. After all, mathematics is the deep underlying structure on which our physical environment is based, but it’s important to try and take a student centered learning approach and make connections between the math classroom, mathematics education and everyday life.

For some topics, such as ratios, this is easy.

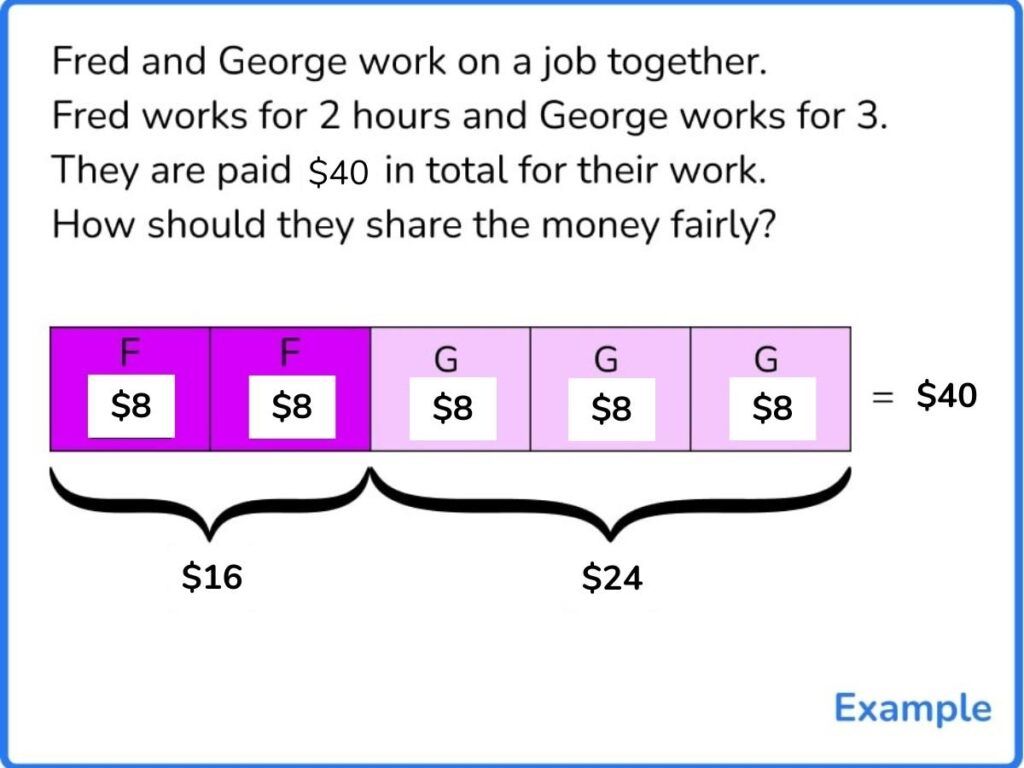
For example, two people complete a job, one works for three hours, the other only works two, how do they split a $50 payment fairly?

Math students can engage with this and debate why it isn’t fair to split the money 50:50 down the middle, particularly if you select a couple of students to play the parts of the workers.

For other topics, be careful that your real-world examples are relevant to the grade-level. I’m thinking about things like using trigonometry to calculate the safe angle of a ladder.

While this is a valid real-life application of trigonometry, safe working angles are unlikely to be something that your average 13-year-old needs to think about!

Again, consider cognitive overload. Our ratio scenario is going to add a bit of extra processing, but a middle school student is likely to have experience with sharing money or objects and the idea of fair and unfair sharing.

These ideas will be easier to think about/process and the scenario becomes useful for enhancing understanding.

Where there’s a relevant real-world connection that students have direct experience of, or are likely to understand with little-to-no additional information can be a nice way into a new math concept.

I’d recommend saving the applications for more abstract ideas until students are more familiar with the concepts behind them.

8. Use worked examples

The type of examples we provide our students can significantly influence how easily they grasp new math concepts. Good math problem worked examples make math instruction more effective and result in better understanding.

Fraction addition example: worked example hierarchy

So, for fraction addition, this might go as follows:

• Adding two fractions with unit numerators;

• Adding two fractions where one denominator is a multiple of another;

• Adding two fractions with any two denominators;

• Adding three fractions / subtracting fractions / improper and mixed numbers (depending on foundational knowledge).

Working this way removes a lot of initial cognitive load, particularly for those students who have gaps in knowledge.

When working with unit fractions, we’re only worrying about sorting denominators. Then, when looking at situations where one denominator is a multiple of the other, it’s easier to ‘spot’ the common denominator to use.

This also means that students whose multiplication recall isn’t great aren’t worrying about multiples, and can attend to the underlying concepts of fraction addition.

I’d judge the number of necessary examples (and the speed at which to work through them) from the student’s prior knowledge and how they did with their starting point assessment.

For some classes, a brief overview would be sufficient. For others, it might be necessary to break it up into chunks over several lessons:

• First covering unit denominators;

• Then giving students an opportunity to practice this;

• Then moving on to denominators with multiples, and so on.

---

9. Incorporate guided practice and faded examples

When I first started teaching, my process for worked examples was:

• I do one on the board and check for general understanding;

• They’re still confused, so I do another one;

• Some of them are ready to go now, but half of them are still lost, so we do another one as a class;

• Most of them are now getting fidgety, so I set them off on the practice task, then try to rush around to all the students who are still stuck and teach them again individually, inevitably wearing myself out and giving myself a headache!

This process was not particularly effective! I gradually tweaked my process over the years, incorporating a couple of key elements, guided practice and faded examples.

Method 1: guided practice

Guided practice or ‘I do, we do, you do’ is a great tool for supporting the learning of any skill, not just math skills.

It’s also closely related to how we appear to learn new skills or concepts naturally. Let’s take the example of a baby learning to walk.

1. First, they observe the people around them;

2. Then, they try to copy with support;

3. Next, they take the first few wobbly steps on their own;

4. Finally, they progress to confident walking, then running.

Method 2: faded examples

Faded examples are ones where scaffolding is gradually removed.

1. The first example presented has all steps complete;

2. The next example omits a stage for students to fill in;

3. The next leaves out more steps, until students complete the task independently.

The stage(s) omitted can be at any point in the process, and will probably depend on the topic being taught. 

A work in progress: using worked example methods in practice

Now, my examples process looks a bit like this:

• I do an example on the board, sometimes in silence, sometimes with an explanation (depending on the topic/class/starting points);

• We discuss the example and pull out key points through effective questioning;

• I work through a second example using the same process, but ask them to join in to complete the final step on their whiteboards (we do);

• We discuss and look for any misconceptions/problems;

• We look at a third example, with minimal guidance from me, except perhaps the starting step or a hint (we do);

• Students complete another couple of practice problems on their whiteboards, showing me after each one. This allows me to pick up on those who still have misconceptions that need addressing (you do);

• Students begin the independent task, while I support those who are still struggling. At this point, there should be less than five of them, so I get them in a small group and re-teach.

---

10. Master math basics before problem-solving

I’m only going to include a very brief discussion about reasoning and problem solving here due to the scope of this article; this is not to trivialize the very complex issue of ‘teaching problem solving’.

Applying skills to unfamiliar math problems is something that students really struggle with. Check out Willingham 2009 ‘Why don’t students like school’ (excerpt) for an explanation of why this is a problem inherent to our brain structure and not a deficit particular to teenagers!

My key takeaway for problem-solving is this: don’t ask students to solve problems when they’ve just met a topic for the first time.

They’re unlikely to have well-formed concepts in their long-term memory to draw upon, and the cognitive load of trying to simultaneously process new information and also solve unfamiliar problems using these ideas will be too great.

This often results in very limited success and a spiral of:

• “I don’t get math”

• “I don’t understand any of this”

• “I’m bad at math”

When looking to improve students’ problem-solving skills, I’d try to select a topic I know they’d ideally mastered, or at least mostly understood and were fairly confident with.

This can be a good opportunity to revisit prior knowledge from previous topics. Frequently recalling information from long-term memory means it is less likely to be forgotten.

---

And there you have it; 10 essential processes for teachers and students to work through together, whatever stage they’re at!

We’ve only explored teaching math for new concepts. It’s equally important to plan your teaching so that topics are revisited frequently at the appropriate spacing.

This ensures that all the hard work on developing conceptual understanding isn’t lost because students forget what they’ve learned.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by a former secondary Maths teacher Christine Norledge and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.