Converting units of area and volume

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Conversion of units Area of rectangles Decimals

Volume

Multiplication and division

Converting metric units Surface area

This topic is relevant for:

GCSE Maths Ratio and Proportion Units Of Measurement

Converting Units Of Area And Volume

Here we will learn about converting units of area and volume.

There are also worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is converting units of area and volume?

Converting units of area and volume is converting between different units from the metric system involving area and volume.

To do this we need to be able to convert between different units of length, and then adapt them for area and volume.

What is converting units of area and volume?

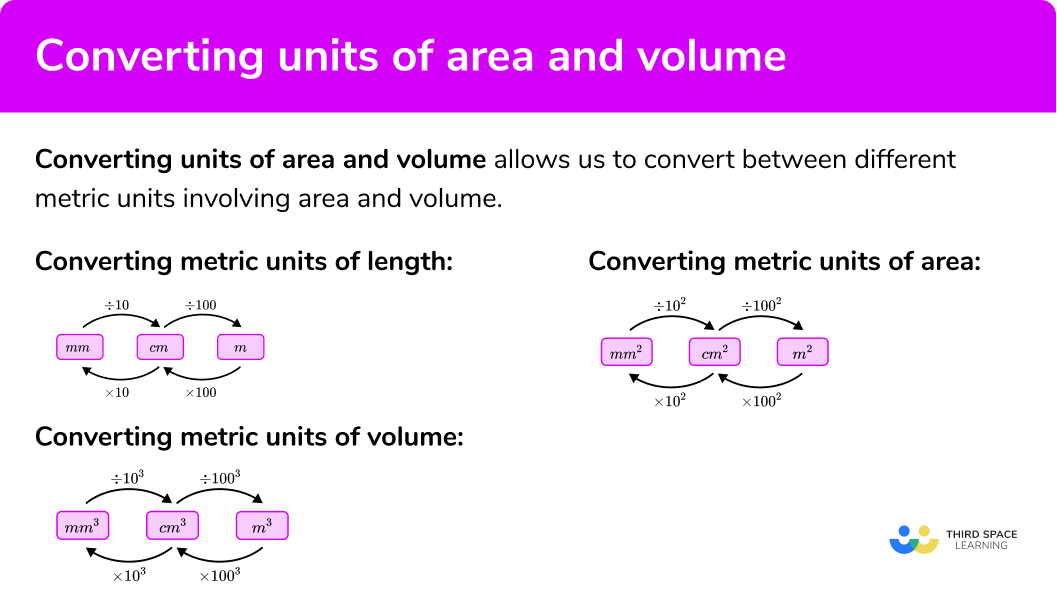
Units of length

We know that $1 \ m =100 \ cm$ and $1 \ cm =10 \ mm$ , so we can convert between these lengths:

Converting units of area and volume Image 1

Step-by-step guide: Converting metric units

We can then apply these to units of measurement for area and volume.

Units of area

Let’s apply this to area:

We know that $1 \ cm = 10 \ mm$

Converting units of area and volume Image 2

So, $1 \ cm^2 = 10 \times 10 =10^2 =100 \ mm^2$

Similarly we know that $1 \ m = 100 \ cm$

So, $1 \ m^2 = 100 \times 100 =100^2 =10 \ 000 \ cm^2$

Converting units of area and volume Image 3

Units of volume

Let’s apply this now to volume:

We know that $1 \ cm =10 \ mm$

Converting units of area and volume Image 4

So, $1 \ cm^3 =10 \times 10 \times 10 =10^3 =1000 \ mm^3$

Similarly we know that $1 \ m = 100 \ cm$

So, $1 \ m^3 =100 \times 100 \times 100 =100^3 =1 \ 000 \ 000 \ cm^3$

Converting units of area and volume Image 5

E.g.

Convert $7 \ m^2$ to $cm^2$

7\times 100^2 =70\ 000

So, $7 \ m^2 = 70 \ 000 \ cm^2$

How to convert units of area and volume

In order to convert units of area and volume:

Find the unit conversion.
Square or cube the unit conversion.
Multiply or divide.

How to convert units of area and volume

Converting units of area and volume worksheet

Get your free converting units of area and volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Converting units of area and volume worksheet

Get your free converting units of area and volume worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on units of measurement

Converting units of area and volume is part of our series of lessons to support revision on units of measurement. You may find it helpful to start with the main units of measurement lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Converting units of area examples

Example 1: converting square metres and square centimetres

Convert $3 \ m^2$ to $cm^2$

Find the unit conversion.

The units involve metres and centimetres

1 \ m=100 \ cm

2Square or cube the unit conversion.

The question involves square units, so we need to square the unit conversion.

100^2 = 10\ 000

3Multiply or divide.

As we are going from larger units to smaller units we multiply.

3 \times 100^2 = 3 \times 10 \ 000=30 \ 000

So, $\ 3 \ m^2 \$ is $\ 30 \ 000 \ cm^2$

Example 2: converting square metres and square centimetres

Convert $45 \ 000 \ cm^2$ to $m^2$

Find the unit conversion.

The units involve metres and centimetres

$1 \ m= 100 \ cm$

Square or cube the unit conversion.

The question involves square units, so we need to square the unit conversion.

$100^2 =10 \ 000$

Multiply or divide.

As we are going from smaller units to larger units we divide.

$45 \ 000 \div 100^2 =45 \ 000 \div 10 \ 000 =4.5$

So, $\ 45 \ 000 \ cm^2 \$ is $\ 4.5 \ m^2$

Example 3: converting square centimetres and square millimetres

Convert $6.1 \ cm^2$ to $mm^2$

Find the unit conversion.

The units involve centimetres and millimetres

$1 \ cm= 10 \ mm$

Square or cube the unit conversion.

The question involves square units, so we need to square the unit conversion.

$10^2 =100$

Multiply or divide.

As we are going from larger units to smaller units we multiply.

$6.1 \times 10^2 = 6.1 \times 100 =610$

So, $\ 6.1 \ cm^2 \$ is $\ 610 \ mm^2$

Example 4: converting square centimetres and square millimetres

Convert $7800 \ mm^2$ to $cm^2$

Find the unit conversion.

The units involve centimetres and millimetres

$1 \ cm= 10 \ mm$

Square or cube the unit conversion.

The question involves square units, so we need to square the unit conversion.

$10^2 =100$

Multiply or divide.

As we are going from smaller units to larger units we divide.

$7800 \div 10^2 =7800 \div 100 = 78$

So, $\ 7800 \ mm^2 \$ is $\ 78 \ cm^2$

Example 5: converting cubic centimetres and cubic millimetres

Convert $5 \ cm^3$ to $mm^3$

Find the unit conversion.

The units involve centimetres and millimetres

$1 \ cm = 10 \ mm$

Square or cube the unit conversion.

The question involves cubic units, so we need to cube the unit conversion.

$10^3 =1000$

Multiply or divide.

As we are going from larger units to smaller units we multiply.

$5 \times 10^3 =5 \times 1000=5000$

So, $\ 5 \ cm^3 \$ is $\ 5000 \ mm^3$

Example 6: converting cubic centimetres and cubic millimetres

Convert $68 \ 000 \ mm^3$ to $cm^3$

Find the unit conversion.

The units involve centimetres and millimetres

$1 \ cm = 10 \ mm$

Square or cube the unit conversion.

The question involves cubic units, so we need to cube the unit conversion.

$10^3 = 1000$

Multiply or divide.

As we are going from smaller units to larger units we divide.

$68 \ 000 \div 10^3 =68 000 \div 1000=68$

So, $\ 68 \ 000 \ mm^3 \$ is $\ 68 \ cm^3$

Common misconceptions

Remember to square or cube the unit conversion

You need to remember to square the unit conversion for units of area.

You need to remember to cube the unit conversion for units of volume.

E.g. convert $3 \ m^2$ to $cm^2$

This would be incorrect $\; \color{red} ✘$

$3 \times 100=300$

This would be correct $\; \color{green} ✔$

$3 \times 100^2 =3 \times 10 \ 000 = 30 \ 000$

$3 \ m^2 =30 \ 000 \ cm^2$

Practice converting units of area questions

5\ 600 \ cm^2

56\ 000 \ cm^2

560 \ cm^2

560\ 000 \ cm^2

We need to multiply by $100^2$ as we are converting $m^2$ to $cm^2$

5.6\times 100^2 = 5.6 \times 10\ 000 = 56\ 000

84\ 000 \ m^2

840 \ m^2

8\ 400 \ m^2

84 \ m^2

We need to divide by $100^2$ as we are converting $cm^2$ to $m^2$

840\ 000\div 100^2 = 840\ 000\div 10\ 000 = 84

9.4 \ mm^2

940 \ mm^2

9\ 400 \ mm^2

0.94 \ mm^2

We need to multiply by $10^2$ as we are converting $cm^2$ to $mm^2$

94\times 10^2 = 94\times 100 = 9 \ 400

5.7 \ cm^2

57 \ cm^2

0.57 \ cm^2

5\ 700 cm^2

We need to divide by $10^2$ as we are converting $mm^2$ to $cm^2$

570\div 10^2 = 570\div 100 = 5.7

63 \ mm^3

630 \ mm^3

0.63 \ mm^3

6\ 300 \ mm^3

We need to multiply by $10^3$ as we are converting $cm^3$ to $mm^3$

6.3\times 10^3 = 6.3\times 1000 = 6\ 300

91\ 000 \ cm^3

91 \ cm^3

9.1 \ cm^3

910 \ cm^3

We need to divide by $10^3$ as we are converting $mm^3$ to $cm^3$

9 \ 100\div 10^3 = 9 \ 100\div 1000 = 9.1

Converting units of area GCSE questions

1. Write $35 \ cm^3$ in $mm^3$

(2 marks)

Show answer

35\times 10^3

(1)

35 \ 000

(1)

2. Write $48 \ m^2$ in $cm^2$

(2 marks)

Show answer

48\times 100^2

(1)

480 \ 000

(1)

3. In the garden there is an area that needs covering with bark chippings.

The area is $210 \ 000 \ cm^2.$

A bag of bark chippings covers $4 \ m^2.$

How many bags of bark chippings are needed to be bought to cover the area?

(3 marks)

Show answer

210\ 000\div 100^2=21

(1)

21\div 4=5.25

(1)

$6$ bags are needed to be bought.

(Rounding up as we can only buy full bags.)

(1)

Learning checklist

You have now learned how to:

Convert metric units of area

Convert metric units of volume

The next lessons are

Did you know?

There are non-metric units of area and non-metric units of volume.

These are called imperial units.

Imperial units of area
There are non-metric units that can be used for area.
E.g.
There are $12$ inches in $1$ foot.
If we wanted to convert between square inches and square feet we would use the multiplier $12^2$ .
So $5$ square feet would be $5 \times 12^2$ square inches which is $720$ square inches.
We can do a similar thing for square feet and square yards.
E.g.
There are $3$ feet in $1$ yard, so we would use $3^2$ to convert between square feet and square yards.
This can be extended to the square mile.
E.g.
There are $1760$ yards in $1$ mile, so we would use $1760^2$ to convert between square feet and square miles.

Imperial units of volume
There are non-metric units that can be used for volume.
E.g.
There are $12$ inches in $1$ foot.
If we wanted to convert between cubic inches and cubic feet we would use the multiplier $12^3$ .
So $4$ cubic feet would be $4 \times 12^3$ cubic inches which is $6912$ cubic inches.
We can do similar for cubic feet and cubic yards.
E.g.
There are $3$ feet in $1$ yard, so we would use $3^3$ to convert
between cubic feet and cubic yards.

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.