High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Multiplication Division Converting units of time Converting metric units Rearranging equations Substitution

Math resources Ratio and proportion

Compound measures

Mass from D and V

Mass from density and volume

Here you will learn about mass from density and volume, including what mass, density and volume are, how to solve for mass and how to identify the units of mass.

Students will first learn about mass from density and volume as part of algebra in high school.

What is mass from density and volume?

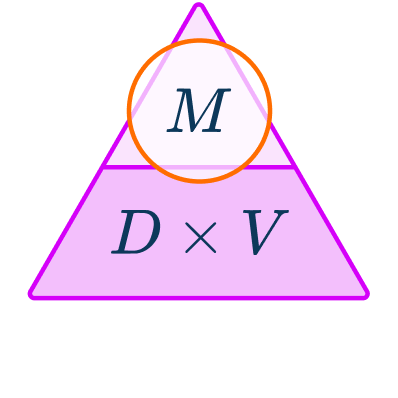
You can calculate mass from density and volume by using the formula,

$M=D\times{V}$

where $\textbf{M}$ represents mass, $\textbf{V}$ represents volume and $\textbf{D}$ represents density of an object.

This is the density equation or density formula rearranged to make mass the subject. You can also represent this using the density mass volume triangle,

[FREE] Ratio Worksheet (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of working with ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Ratio Worksheet (Grade 6 to 7)

DOWNLOAD FREE

Mass

The mass of an object is the amount of matter there is in an object.

The standard $SI$ unit of mass is kilograms $(kg)$ , but we can also use other metric units such as grams, milligrams or tonnes.

The following table shows the conversion of $1\mathrm{~kg}$ to these other units.

Customary units include pounds $(lb),$ ounces $(oz)$ and imperial tons $(ton).$

The customary ton is not the same as the metric tonne, as $1 \, ton=1.01605 \, t.$

Mass calculator

The mass of an object can be calculated with the density and volume of the object.

Mass is directly proportional to the volume of an object with a constant density; the heavier the mass, the larger the volume when the density remains the same.

This means that $M=kV$ where the constant of proportionality, $k,$ represents the density of the object.

Volume

The volume of an object is how much space an object or substance takes up.

The $SI$ unit for volume is cubic meters written as $m^3.$ Other volume units are the cubic centimeter $(cm^3)$ and the cubic millimeter $(mm^3).$

The volume of a liquid is referred to as its capacity where $1 \, cm^3=1 \, ml \, (1$ milliliter $),$ and so $1000 \, cm^3=1 \, L \, (1$ liter $).$

Volume calculator

The volume of a substance can be calculated with the density and mass of the object.

Volume is inversely proportional to the density of an object with a constant mass; the greater the volume, the lower the density of the object or substance with a constant mass.

This means that, for volume $V$ and density $D, \, V=\cfrac{k}{D}$ where the constant of proportionality, $k,$ represents the mass of the object.

See also: Volume

Density

Density is another physical property of an object or substance. The density of a material is a compound measure that relates how much matter there is in the substance per unit volume.

For example, a sponge has a higher density when it is squeezed as its volume has decreased, but the mass has not changed. Conversely, when the sponge has been released, it has a lower density as the volume has increased but the mass has stayed the same.

Below is a table describing some density measurements.

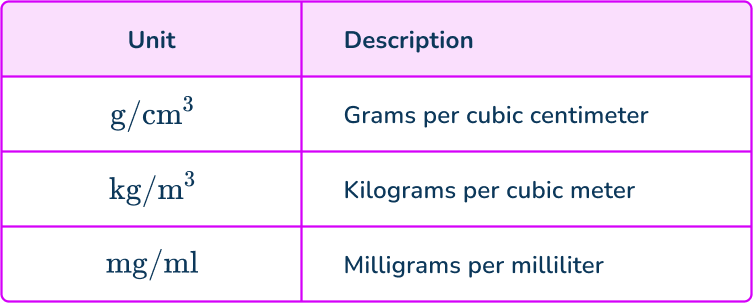
Notice that the first unit of each density unit is a mass (grams, kilograms, milligrams) and the divisor is a volume measurement (cubic centimeters, cubic meters, and milliliters).

Remember: $1 \, cm^3=1 \, ml.$

At $4^{\circ}C,$ the density of water is $1000 \, kg/m^{3},$ which is the same as $1 \, g/cm^{3}.$

Density calculator

The density of a substance can be calculated with the volume and mass of the object.

Density is inversely proportional to the volume of an object with a constant mass; the greater the density, the lower the volume of the object or substance with a constant mass.

This means that, for density $D$ and volume $V, \, D=\cfrac{k}{V}$ where the constant of proportionality, $k,$ represents the mass of the object.

What is mass from density and volume?

Common Core State Standards

How does this relate to high school math?

Algebra – Creating Equations (HS-A.CED.A.4)
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law $V=IR$ to highlight resistance $R.$

Number and Quantity – Quantities (HS-N.Q.A.1)
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.

How to find mass from density and volume

In order to find mass from density and volume:

Write the formula with the correct subject.
Substitute known values into the formula and do the calculation.
Write down the solution including the units.

How to find mass from density and volume examples

Example 1: calculate mass in grams

Find the mass of an object with volume $300 \mathrm{~cm}^3$ and density $5 \mathrm{~g}/\mathrm{cm}^3.$

Write the formula with the correct subject.

To calculate the mass, multiply the density of the substance by the volume of the object.

M=D\times{V}

2Substitute known values into the formula and do the calculation.

M=D \times V=300 \times 5=1,500

3Write down the solution including the units.

Let’s look at how the units were calculated.

The units for density here are grams per cubic centimeter, $\mathrm{g/cm}^{3}.$

The units for volume here are cubic centimeters, $\mathrm{cm}^{3}.$

As density is multiplied by volume to get mass, the units are

\cfrac{\mathrm{g}}{\mathrm{cm}^3}\times\mathrm{cm}^3=\cfrac{g}{\mathrm{cm}^3} \times\cfrac{\mathrm{cm}^3}{1}=g

Note how the centimeters cubed canceled out and left just $g.$ This makes sense, because you are calculating mass, which is measured in $g.$

The mass of the object is $1,500 \mathrm{~g}$ or $1.5 \mathrm{~kg}.$

Example 2: calculate mass in kilograms

Find the mass of an object with volume $450 \mathrm{~m}^3$ and density of the material is $7.2 \mathrm{~kg}/\mathrm{m}^3.$

Write the formula with the correct subject.

To calculate the mass, multiply the density of the substance by the volume of the object.

$M=D\times{V}$

Substitute known values into the formula and do the calculation.

M=D \times V=450 \times 7.2=3,240

Write down the solution including the units.

Let’s look at how the units were calculated.

The units for density here are kilograms per cubic meter, $\mathrm{kg}/\mathrm{m}^3.$

The units for volume here are cubic meters, $\mathrm{m}^{3}.$

As density is multiplied by volume to get mass, the units are

$\cfrac{\mathrm{kg}}{\mathrm{m}^3} \times \mathrm{m}^3=\cfrac{\mathrm{kg}}{\mathrm{m}^3} \times \cfrac{\mathrm{m}^3}{1}=\mathrm{kg}$

Note how the meters cubed canceled out and left just $kg.$ This makes sense, because you are calculating mass, which is measured in $kg.$

The mass of the object is $3,240 \mathrm{~kg}.$

Example 3: calculate mass in milliliters

Find the mass of a solid object with volume $4 \mathrm{~ml}$ and density of the material is $75 \mathrm{~mg}/\mathrm{ml}.$

Write the formula with the correct subject.

To calculate the mass, multiply the density of the substance by the volume of the object.

$M=D\times{V}$

Substitute known values into the formula and do the calculation.

M=D \times V=4 \times 75=300

Write down the solution including the units.

Let’s look at how the units were calculated.

The units for density here are milligrams per milliliter, $mg/ml.$

The units for volume here are milliliters, $ml.$

As density is multiplied by volume to get mass, the units are

$\cfrac{m g}{m l} \times m l=\cfrac{m g}{m l} \times \cfrac{m l}{1}=m g$

Note how the milliliters canceled out and left just $mg.$ This makes sense, because you are calculating mass, which is measured in $mg.$

The mass of the object is $300 \mathrm{~mg}.$

Example 4: calculate mass when units need converting

Find the mass of an object with volume $950 \mathrm{~cm}^3$ and density of the material is $18.2 \mathrm{~g}/\mathrm{cm}^3.$ Write the answer in kilograms.

Write the formula with the correct subject.

M=D \times V

Substitute known values into the formula and do the calculation.

M=D \times V=18.2 \times 950=17,290 \, g

Write down the solution including the units.

The mass is currently in grams, and you need to convert it to kilograms. Do this by dividing the mass by $1000$ since $1000\mathrm{~g}=1\mathrm{~kg}.$

$17,290\div{1,000}=17.29$

Mass $=17.29\mathrm{~kg}$

Example 5: calculate mass when units need converting

Find the mass of an object with volume $0.000875 \mathrm{~m}^3$ and density $15.3 \mathrm{~g} / \mathrm{cm}^3.$

Write the formula with the correct subject.

M=D \times V

Substitute known values into the formula and do the calculation.

The volume unit is in $\mathrm{m}^3$ and the density unit is in $\mathrm{g} / \mathrm{cm}^3,$ so convert the volume to $\mathrm{cm}^3.$ Since $1\mathrm{~m}^3=1,000,000\mathrm{~cm}^3,$ multiply the volume by $1,000,000 \, (=1$ million, or $10^6)$ first, then substitute the values into the formula.

$V=0.000875\times{1,000,000}=875\mathrm{~cm}^3$

Now $V=875\mathrm{~cm}^3$ and $D=15.3\mathrm{~g} / \mathrm{cm}^3$ and so

$M=D \times V=15.3 \times 875=13,387.5\mathrm{~g}$

Write down the solution including the units.

Mass $=13,387.5\mathrm{~g}.$

Example 6: calculate mass with scientific notation units

Find the mass of an object with volume $\left(2 \times 10^7\right) \mathrm{~cm}^3$ and density of the material is $3,100 \mathrm{~kg} / \mathrm{m}^3.$

Write the formula with the correct subject.

M=D \times V

Substitute known values into the formula and do the calculation.

The volume is currently in cubic centimeters, so convert to cubic meters by dividing by $1,000,000.$

$\left(2 \times 10^7\right) \div 1,000,000=2 \times 10^7 \div 10^6=2 \times 10^1=20$

Now $V=20 \, m^3$ and so

$M=D \times V=3,100 \times 20=62,000 \mathrm{~kg}$ or $6.2 \times 10^4 \mathrm{~kg}.$

Write down the solution including the units.

Mass $=62,000 \mathrm{~kg}$ or $6.2 \times 10^4 \mathrm{~kg}.$

Teaching tips for mass from density and volume

Collaborate with the science teachers, so you can teach this skill at the same time as students using it during an Earth Science or Chemistry class.

While worksheets can give students practice manipulating the equation and completing the calculations, be sure to also give students real world examples or projects that require them to calculate the mass to solve a problem.

Completing the calculation is typically not the focus of these lessons, so let students use a calculator to solve. Also encourage students to use the calculator to check their work.

Easy mistakes to make

Incorrectly using the density formula
A useful way to remember the correct orientation is referring to the units for density. For example, the density units $\mathrm{kg} / \mathrm{m}^3,$ so that density equals the mass $(kg)$ divided by the volume $(m^3).$ So when solving for the density, divide the mass by the volume.

Incorrectly converting between units of measure
Often the metric units are used for mass, density and volume. So it is important to be able to convert between metric units such as knowing there are $100\mathrm{~cm}$ in $1$ meter.

Occasionally you might come across other types of units, such as customary units like the cubic foot, so having a conversion strategy for these units is also necessary.

Incorrectly converting units of volume
Volume uses cubic units such as $m^3$ and $cm^3.$ The conversion for cubic units is the cube of the scale factor.

For example, a cube with a side length of $1\mathrm{~m}$ has a volume of $1\mathrm{~m}^3.$ The same cube has a side length of $100\mathrm{~cm},$ and so the volume of the cube is $100^3=1,000,000\mathrm{~cm}^3.$

This means that $1\mathrm{~m}^3=1,000,000\mathrm{~cm}^3$ and so if you convert cubic meters to cubic centimeters, you need to multiply the volume by $1,000,000.$

Practice mass from density and volume questions

\cfrac{c m^3}{g} \times c m^3=\cfrac{c m^3}{g} \times \cfrac{c m^3}{1}=g

\cfrac{\mathrm{g}}{\mathrm{cm}^3}\times\mathrm{cm}^3=\cfrac{g}{\mathrm{cm}^3} \times\cfrac{\mathrm{cm}^3}{1}=g

\cfrac{g}{\mathrm{cm}^3} \times \mathrm{cm}^3=\cfrac{\mathrm{g}}{\mathrm{cm}^3} \times \cfrac{1}{\mathrm{cm}^3}=\mathrm{cm}^3

\cfrac{c m^3}{g} \times g=\cfrac{c m^3}{g} \times \cfrac{g}{1}=c m^3

The units for density here are grams per cubic centimeter, $\mathrm{g/cm}^{3}.$

The units for volume here are cubic centimeters, $\mathrm{cm}^{3}.$

As density is multiplied by volume to get mass, the units are

\cfrac{\mathrm{g}}{\mathrm{cm}^3} \times \mathrm{cm}^3=\cfrac{\mathrm{g}}{\mathrm{cm}^3} \times \cfrac{\mathrm{cm}^3}{1}=\cfrac{\mathrm{g}}{1} \times \cfrac{\mathrm{cm}^3}{\mathrm{cm}^3}=\mathrm{g}

Note how the centimeters cubed canceled out, since $\cfrac{\mathrm{cm}^3}{\mathrm{cm}^3}=1,$ and left just $g.$ This makes sense, because you are calculating mass, which is measured in $g.$

400 \, g

360 \, g

40 \, g

36 \, g

\text { Mass }=\text { density } \times \text { volume }=3 \cfrac{\mathrm{g}}{\mathrm{cm}^3} \times 120 \mathrm{~cm}^3=360 \mathrm{~g}

620 \, g

660 \, g

640 \, g

680 \, g

\text { Mass }=\text { density } \times \text { volume }=4 \cfrac{\mathrm{g}}{\mathrm{cm}^3} \times 170 \mathrm{~cm}^3=680 \mathrm{~g}

1.8 \, kg

2 \, kg

18,000 \, kg

2,000 \, kg

\text { Mass }=\text { density } \times \text { volume }=6,000 \cfrac{\mathrm{kg}}{\mathrm{m}^3} \times 3 \mathrm{~m}^3=18,000 \mathrm{~kg}

10,660 \, g

1,066 \, g

1.066 \, kg

10.66 \, kg

0.00082 \, m^3=820 \, cm^3

\text { Mass }=\text { density } \times \text { volume }=13 \cfrac{\mathrm{g}}{cm}^3 \times 820 \mathrm{~cm}^3=10,660 \mathrm{~g}

Since $1 \, kg=1,000 \, g,$ divide by $1,000$ to convert to kilograms.

10,660\div 1,000 = 10.66 \, kg

600 \, kg

60 \, kg

1,215 \, kg

12,150 \, kg

\text { Mass }=\text { density } \times \text { volume }=2,700 \cfrac{\mathrm{kg}}{\mathrm{m}^3} \times 4.5 \mathrm{~m}^3=12,150 \mathrm{~kg}

To convert to tonnes

12150 \div 1000 = 12.15 \, tonnes

Mass from density and volume FAQs

What is the density formula?

The density formula is $\rho=\cfrac{m}{V},$ where $\rho \, (rho)$ is density, $m$ is mass and $V$ is volume.

What are different units of volume?

Some different units of volume are millimeters cubed $(\mathrm{mm}^3),$ centimeters cubed $(\mathrm{cm}^3),$ meters cubed $(\mathrm{m}^3),$ cubic inches $(\mathrm{inches}^3),$ cubic feet $(\mathrm{ft}^3),$ etc.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.