Dividing Ratios - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Addition and subtraction Multiplication and division Fractions Fractions as division Converting fractions, decimals, and percentages Equivalent fractions

Math resources Ratio and proportion Ratio

Dividing ratios

Here you will learn about dividing ratios, including how to share a quantity in a given ratio and real-life ratio problems.

Students will first learn about dividing ratios as part of ratios and proportional relationships in $6$ th grade.

What is dividing ratios?

Dividing ratios is a way of sharing a quantity in given parts of a ratio. This can also be referred to as “dividing a quantity by a ratio.”

Problems involving dividing ratios can get quite wordy as they typically apply directly to real-life problems, usually involving money or food.

This means that it is likely that you will have to draw out the relevant information from the word problem. You can also expect your answers to be integers (whole numbers), decimals, fractions, or mixed numbers.

[FREE] Ratio Check for Understanding Quiz (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Ratio Check for Understanding Quiz (Grade 6 to 7)

Use this quiz to check your grade 6 to 7 students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!

DOWNLOAD FREE

For example,

Share the amount $\$ 10$ in the ratio $2\text{:}3.$

Here, the quantity is $\$ 10,$ which is being shared in the parts of the ratio, $2$ and $3.$ You need to find an equivalent ratio where the sum of the ratio parts is equal to $10.$

Currently, you know the following facts:

The quantity $=\$ 10$

The ratio $=2\text{:}3$

You need to determine how many shares there are in the ratio overall.

You do this by adding the parts of the ratio together: $2+3=5$ shares.

You have $\$ 10$ being split into $5$ shares, and so you divide the quantity by the total amount of shares of the ratio $10\div5=2.$

This is the value of one share.

So each share is worth $\$ 2.$

If there are $2$ shares in the first part of the ratio, and each share is $\$ 2,$ you multiply these values together to get the amount for that part of the ratio: $2 \times \$ 2=\$ 4.$

Repeating this for the second part of the ratio, you get: $3 \times \$ 2=\$ 6.$

The solution is $\$ 4\text{:}\$ 6$ (in that order).

To check your solution, add the final parts of the ratio together. If it is correct, the total should match the original quantity $\$ 4+\$ 6=\$ 10.$ This is correct.

Note: Don’t be tempted to write your answer in its simplest form; you are finding an equivalent ratio where the parts total the quantity. That being said, it is a good way to check if your solution is correct. $4\text{:}6$ does simplify to $2\text{:}3,$ the original ratio.

Bar modeling

The example above shows the use of bar modeling in how to share a quantity in a given ratio. Let’s have a look at another example using a three-part ratio.

For example,

A bag contains $24$ sweets. Three friends share the sweets in a ratio of $1\text{:}2\text{:}3.$ How many sweets does each person get?

If person $A$ gets $1$ share, person $B$ gets $2$ shares and person $C$ gets $3$ shares, each time the parts are shared, you are using $1+2+3=6$ parts.

Each share is therefore worth $24 \div 6=4.$

If $A$ gets $1$ share, $B$ gets $2$ shares and $C$ gets $3$ shares, you have

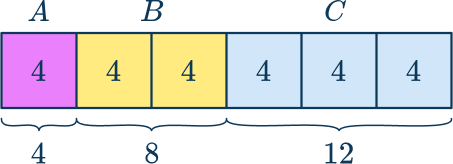
This gives us the ratio $4\text{:}8\text{:}12.$

What is dividing ratios?

Common Core State Standards

How does this relate to $6$ th grade math?

Grade 6 – Ratios and Proportional Relationships (6.RP.A.3)
Use ratio and rate reasoning to solve real-world and mathematical problems, example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

How to divide a quantity by a ratio

In order to divide a quantity by a ratio:

Add the parts of the ratio together.
Divide the quantity by the sum of the parts.
Multiply the share value by each part in the ratio.

Dividing ratios examples

Example 1: standard question

Share the amount $\$ 120$ in the ratio $1\text{:}4.$

Add the parts of the ratio together.

1+4=5

2Divide the quantity by the sum of the parts.

120 \div 5=24

3Multiply the share value by each part in the ratio.

24 \times 1=\$ 24

24 \times 4=\$ 96

Answer: $\$ 24\text{:}\$ 96$

A bag of sweets contains $600$ sweets. The sweets were divided between boys and girls in the ratio $1\text{:}2.$ If there are $25$ girls, how many sweets did each girl receive?

Add the parts of the ratio together.

So you have the amount of $600$ and the ratio $1\text{:}2.$

$1+2=3.$

Divide the quantity by the sum of the parts.

600 \div 3=200

Multiply the share value by each part in the ratio.

200 \times 1=200

$200 \times 2=400$

$400$ sweets were given to the $25$ girls, so

$400 \div 25=16$

Answer: $16$ sweets

Example 3: three part ratio

$30$ glue sticks were divided into $3$ groups in the ratio $3\text{:}2\text{:}1.$ Calculate how many glue sticks each group received.

Add the parts of the ratio together.

3+2+1=6

Divide the quantity by the sum of the parts.

30 \div 6=5

Multiply the share value by each part in the ratio.

5 \times 3=15

$5 \times 2=10$

$5 \times 1=5$

Answer: $15\text{:}10\text{:}5$

Example 4: large quantities

A dealership sells hatchbacks and SUVs. $1,600$ cars were sold in one year at the dealership in the ratio of $3\text{:}2$ of hatchbacks to SUVs. How many hatchbacks were sold?

Add the parts of the ratio together.

3+2=5

Divide the quantity by the sum of the parts.

1600 \div 5=320

Multiply the share value by each part in the ratio.

320 \times 3=960

$320 \times 2=640$

Answer: $960$ hatchbacks

Note: you do not need to work out all of the values in the new ratio but this can be helpful to check your answer is correct as the sum of these values must be the original amount.

Example 5: find one part

Concrete is made from $1$ part cement, $2$ parts sand, and $3$ parts gravel. If Jarred wants to make $900 \, kg$ of concrete, how much sand does he need?

Add the parts of the ratio together.

1+2+3=6

Divide the quantity by the sum of the parts.

900 \div 6=150

Multiply the share value by each part in the ratio.

150 \times 2=300 \mathrm{~kg}

Answer: $300\mathrm{~kg}$ of sand

Example 6: recipe

A cocktail is made from mixing pineapple juice, orange juice, and sparkling water in the ratio $300\mathrm{~ml}\text{:}700\mathrm{~ml}\text{:}0.5\mathrm{~L}.$ How much of each quantity would be needed to make $6\mathrm{~L}$ of cocktail?

Add the parts of the ratio together.

All the units must be the same in the ratio. $0.5\mathrm{~L}=500\mathrm{~ml}$ sparkling water, so the ratio of pineapple to orange to sparkling water is $300\text{:}700\text{:}500.$ This means the total is equal to

$300+700+500=1500\mathrm{~ml}=1.5\mathrm{~L}$

Divide the quantity by the sum of the parts.

6 \div 1.5=4

Multiply the share value by each part in the ratio.

4\times{300}=1200\mathrm{~ml}

$4\times{700}=2800\mathrm{~ml}$

$4\times{500}=2000\mathrm{~ml}$

Answer:

$1,200\mathrm{~ml}$ of pineapple juice $(=1.2\mathrm{~L})$

$2,800\mathrm{~ml}$ of orange juice $(=2.8\mathrm{~L})$

$2,000\mathrm{~ml}$ of sparkling water $(=2\mathrm{~L})$

Example 7: bar modeling

The bar model below shows the ratio of the length of time the red, yellow, and green traffic lights are on during one sequence.

In one day, how many hours is each light on?

Add the parts of the ratio together.

Adding up the number of shares in the bar, you have $3+2+5=10$ .

Divide the quantity by the sum of the parts.

A day has $24$ hours, and so $24 \div 10=2.4$ .

Each share represents $2.4$ hours.

Multiply the share value by each part in the ratio.

Looking at each color, you have

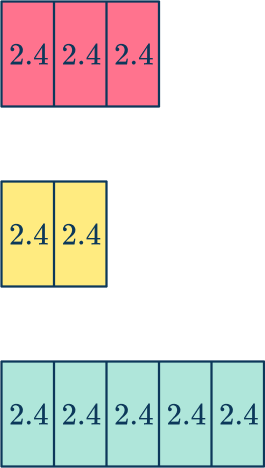
Red: $2.4 \times 3=7.2$ hours

Yellow: $2.4 \times 2=4.8$ hours

Green: $2.4 \times 5=12$ hours

Answer

Red $=7.2$ hours ( $7$ hours $12$ minutes)

Yellow $=4.8$ hours ( $4$ hours $48$ minutes)

Green $=12$ hours

How to find the whole quantity given the amount of one part

In order to find the whole quantity given the amount of one part of the ratio:

Divide the amount by the correct part of the ratio.
Multiply the share value by the other parts in the ratio.
Add the amounts from each part of the ratio.

Example 8: being given one part of the ratio

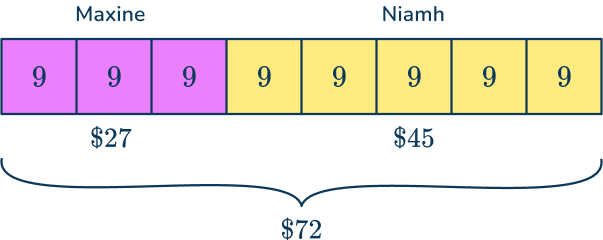
Maxine and Niamh share some money in the ratio $3\text{:}5.$ Niamh receives $\$ 45.$ How much money was shared?

Divide the amount by the correct part of the ratio.

You have been told that $5$ parts are $\$ 45.$ So you divide $\$ 45$ by $5$ to find the value of each share.

$45 \div 5=9$

Each share represents $\$ 9.$

Multiply the share value by the other parts in the ratio.

You can now work out Maxine’s part.

$3 \times 9=\$ 27$

Add the amounts from each part of the ratio.

Maxine has $\$ 27$ and Niamh has $\$ 45$ , so

$\$ 27+\$ 45=\$ 72$

Answer: $\$ 72$ was shared between Maxine and Niamh.

Here is the question as a bar model.

Teaching tips for dividing ratios

Be sure that students understand the fundamentals of ratios before introducing dividing ratios.
Step-by-step guide: Ratio
Step-by-step guide: How to write a ratio

Use word problems that relate to real life. For instance, if a recipe calls for a ratio of $2\text{:}3$ (flour to sugar) and you need to divide this ratio for a smaller batch, show how to apply the division in context.

If students are struggling, explain that dividing ratios relates to fractions because ratios can be expressed as fractions, and dividing a ratio is the same as dividing corresponding fractions.

For example, dividing the ratio $4\text{:}5$ by $2$ is like dividing the fraction $\cfrac{4}{5}$ by $2,$ which simplifies to $\cfrac{2}{5}.$

As you can see, the first number of the ratio is the same as the numerator of the fraction, and the second number of the ratio is the denominator of the fraction. The quotient represents the new ratio after division.

Solve several worksheet problems together as a class. Start with simple examples and gradually increase complexity.

Easy mistakes to make

Ratios and fractions confusion
Take care when writing ratios as fractions and vice versa. Most ratios you come across are $\text{part}\text{:}\text{part}$ and not $\text{part}\text{:}\text{total number of parts.}$

The ratio here of $\text{red}\text{:}\text{yellow}$ is $1\text{:}2.$ So the fraction which is red is $\cfrac{1}{3}$ (not $\cfrac{1}{2}$ ) because $1$ out of a total of $3$ parts are red.

Dividing the ratio by each part
As you need to divide something, it is incorrectly assumed that the amount is divided by each part of the ratio separately. Take for example $“$ divide $\$ 120$ in the ratio $2\text{:}3”.$

The answer is created by dividing $\$ 120$ by $2,$ and then $\$ 120$ by $3$ to get $\$ 60\text{:}\$ 40.$

This does not make sense as the answer ratio is not equivalent to the original ratio. Instead, the amount is divided by the sum of the parts in the ratio $120 \div(2+3)=120 \div 5=\$ 24,$ and then multiplied by each part in the ratio $24 \times 2=\$ 48,24 \times 3=\$ 72.$

Mixing units or using the wrong units
Make sure that all the units in the ratio are the same. For example, in example $6,$ the answer shows the units in the ratio were in milliliters OR liters. You did not mix $ml$ and $L$ in the ratio.

Not knowing what numbers to use
Knowing what each number represents is very important for these types of questions. If you get confused, write the units down on each line of work.

Counting the number of parts in the ratio, not the total number of shares
The ratio $5\text{:}4$ has $9$ shares and $2$ parts. This is because the ratio contains $2$ numbers but the sum of these parts (the number of shares) is $5+4=9.$

You need to find the value per share, so you need to use the $9$ shares in your next line of work.

Simplifying the answer
When sharing a quantity in a given ratio, you are finding an equivalent ratio. You do not need to simplify the answer.

Practice dividing ratios questions

\$ 1900\text{:}\$ 1710

\$ 200\text{:}\$ 180

\$ 180\text{:}\$ 200

\$ 10\text{:}\$ 9

Amount: $\$ 380$

Ratio: $10\text{:}9$

\begin{aligned}&10+9=19 \\\\ &\$ 380\div{19}=20 \\\\ &20\times{10}=\$ 200 \\\\ &20\times{9}=\$ 180 \end{aligned}

\$ 9\text{:}\$ 11

\$ 36000\text{:}\$ 36000

\$ 32400\text{:}\$ 39600

\$ 39600\text{:}\$ 32400

Amount: $\$ 72,000$

Ratio: $45\text{:}55 \, (=9\text{:}11)$

\begin{aligned}&9+11=20 \\\\ &72000\div{20}=\$ 3600 \\\\ &3600\times{9}=\$ 32400 \\\\ &3600\times{11}=\$ 39600 \end{aligned}

3408

2556

1704

1917

Amount: $7668$

Ratio: $2\text{:}3\text{:}4$

\begin{aligned}&2+3+4=9 \\\\ &7668\div{9}=852 \\\\ &852\times{2}=1704 \, (Males) \\\\ &852\times{3}=2556 \, (Females) \\\\ &852\times{4}=3408 \, (Children) \end{aligned}

Answer: $3408$ members are children

18750\text{:}21429

70,000\text{:}80,000

80,000

80,000\text{:}70,000

Amount: $150,000$

Ratio: $8\text{:}7$

\begin{aligned}&8+7=15 \\\\ &150,000\div{15}=10,000 \\\\ &10,000\times{8}=80,000 \\\\ &10,000\times{7}=70,000 \end{aligned}

3900\text{:}1050\text{:}50

78\text{:}21\text{:}1

1050\mathrm{~ml}=1.05\mathrm{~L}

3900\mathrm{~ml}=3.9\mathrm{~L}

Amount: $5\mathrm{~L}=5000\mathrm{~ml}$

Ratio: $78\text{:}21\text{:}1$

\begin{aligned}&78+21+1=100 \\\\ &5000\div{100}=50 \\\\ &50\times{21}=1050 \end{aligned}

The amount of oxygen is $1050\mathrm{~ml}$ or $1.05\mathrm{~L}.$

450\mathrm{~g}

1350\mathrm{~g}

600\mathrm{~g}

2700\mathrm{~g}

Amount of butter: $900\mathrm{~g}$

Part of the ratio for butter: $2$

Part of the ratio for flour: $3$

$900\div{2}=450\mathrm{~g}$ ( $1$ share)

$450\times{3}=1350\mathrm{~g}$ (amount of flour)

Dividing ratios FAQs

What does it mean to divide a ratio?

Dividing ratios is a way of sharing a quantity in given parts of a ratio.

How do you divide a quantity by a ratio?

To divide a quantity by a ratio, first you add the parts of the ratio together, then divide the quantity by the sum of the parts, and finally, multiply the share value by each part in the ratio.

How is dividing ratios similar to dividing fractions?

Dividing ratios is similar to dividing fractions because ratios can be expressed as fractions, and you divide the ratio by treating it like a fraction. For example, dividing the ratio $5\text{:}6$ by $2$ is like dividing the fraction $\cfrac{5}{6}$ by $2.$

Why is dividing ratios useful in real life?

Dividing ratios is useful in real-life situations such as resizing recipes, splitting expenses, or adjusting proportions in construction projects, as it helps maintain the correct balance between quantities.

The next lessons are

Proportion
Converting fractions decimals and percents
Percents

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.