High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Multiplication Division Converting units of time Converting metric units Rearranging equations SubstitutionDensity mass volume triangle
Here you will learn about mass, density and volume, including what they are and how they are related to each other.
Students will first learn about the density mass volume triangle as part of algebra in high school.
What is the density mass volume triangle?
Mass, density and volume are physical properties of objects.
- \underline{Mass}
Mass is the measurement of the amount of matter there is in an object. The units of mass are usually kilograms (kg) or grams (g). The kilogram is the SI unit (the International System of Units) for mass.
- \underline{Volume}
Volume is a measure of how much space an object takes up. The volume of a substance is often measured in cubic centimeters ({cm}^3). The derived SI unit for volume is the cubic meter ({m}^3).
- \underline{Density}
Density is a compound measure made from the ratio of mass and volume. Density is a measure of the amount of matter there is per unit volume. The SI unit for density is kilograms per cubic meter (\mathrm{kg/m}^3 ).
Imagine there are two objects of the same size. The first object has high density, the second object has a lower density.
The object with high density would feel heavier than the object with the lower density. You could try this with two water bottles that are the same size. Fill one with water and fill the other with air.
The density of water is approximately 1,000\mathrm{~kg/m}^{3}.
The density of air is approximately 1.225\mathrm{~kg/m}^{3}.
The density of water is greater than the density of air, so the bottle filled with water is heavier.
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
[FREE] Ratio Worksheet (Grade 6 to 7)
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!
DOWNLOAD FREE![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
[FREE] Ratio Worksheet (Grade 6 to 7)
![[FREE] Ratio Worksheet (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
Use this quiz to check your grade 6 to 7 students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!
DOWNLOAD FREEDensity
To calculate the mass, density or volume of an object, use the formula:
\text{Density}=\cfrac{\text{Mass}}{\text{Volume}}
This can be written as a formula triangle:

where M is the mass, D is the density, and V is the volume of an object.
Using this triangle, you can derive the formulas:
- M=D\times{V}
- D=M\div{V}
- V=M\div{D}
Note: The relative density, or specific gravity is the relationship between the density of a substance in relation to the density of another referenced substance.
For example, water at 4℃ has a density of 1\mathrm{~kg/L}. Liquid mercury has a density of 13.6\mathrm{~kg/L} and so its specific gravity is 13.6 as 13.6\div{1}=13.6. Since both units are in \mathrm{kg/L}, specific gravity has no units.
What is the density mass volume triangle?
Common Core State Standards
How does this relate to high school math?
- Algebra – Creating Equations (HS-A.CED.A.4)
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. For example, rearrange Ohm’s law V=IR to highlight resistance R.
- Number and Quantity – Quantities (HS-N.Q.A.1)
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
How to find the density, mass or volume
In order to find density, mass or volume:
- Write the formula with the correct subject.
- Substitute known values into the formula and do the calculation.
- Write down the solution including the units.
Density mass volume triangle examples
Example 1: calculating the density (g/cm³)
A sphere is made from gold. It has volume 3\mathrm{~cm}^{3} and mass 60\mathrm{~g}. Calculate the density of the object.
- Write the formula with the correct subject.
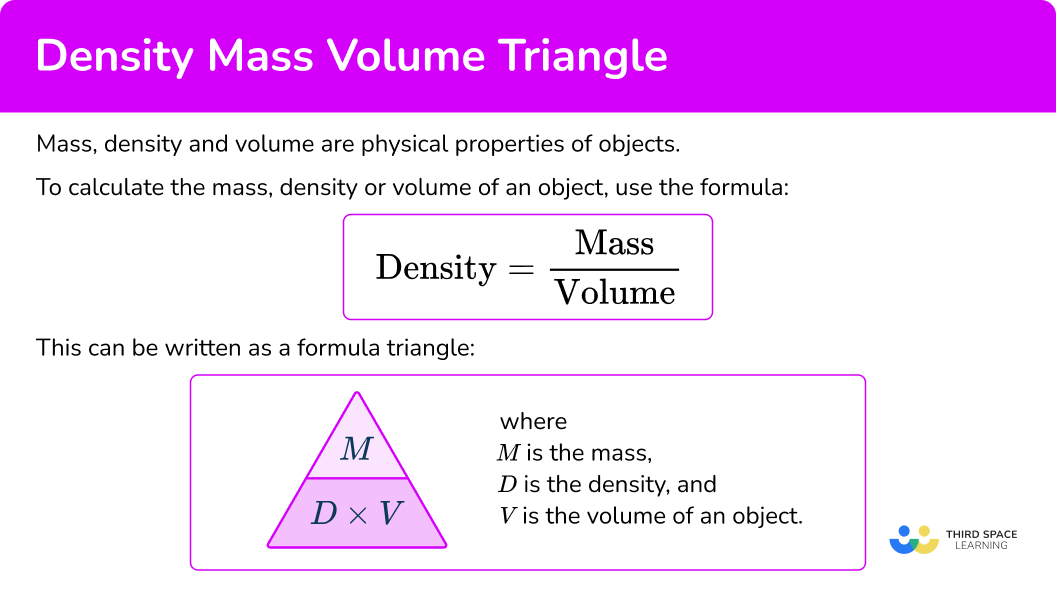
To calculate the density, divide the mass of the sphere by the volume of the sphere.
2Substitute known values into the formula and do the calculation.
D=\cfrac{M}{V}=\cfrac{60}{3}=203Write down the solution including the units.
The units for mass here are grams \mathrm{g}.
The units for volume here are cubic centimeters, \mathrm{cm}^{3}.
As mass is divided by volume to get density, the units are \mathrm{g}\div\mathrm{cm}^{3}=\mathrm{g/cm}^{3}.
The density of the object is 20\text{ g/cm}^{3}.
Example 2: calculating the density (kg/m³)
An object is made from steel. It has a volume of 25\mathrm{~m}^{3} and a mass of 425\mathrm{~kg}. Calculate the density of the object.
Write the formula with the correct subject.
To calculate the density, divide the mass of the object by the volume of the object.

D=\cfrac{M}{V}
Substitute known values into the formula and do the calculation.
Write down the solution including the units.
The units for mass here are kilograms \mathrm{kg}.
The units for volume here are cubic meters, \mathrm{m}^{3}.
As mass is divided by volume to get density, the units are \mathrm{kg}\div\mathrm{m}^{3}=\mathrm{kg/m}^{3}.
The density of the object made of steel is 17\mathrm{~kg/m}^{3}.
Example 3: calculating the volume (cm³)
The mass of an object is 600\mathrm{~g}. The density of the substance which the object is made from is 3.2\mathrm{~g/cm}^{3}. Calculate the volume of the object.
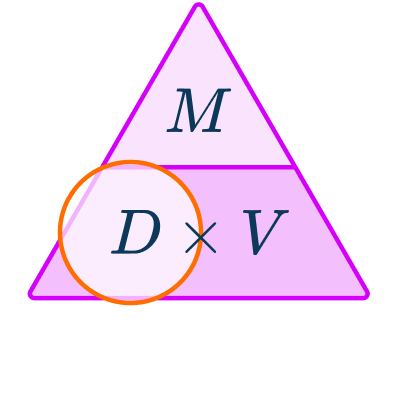
Write the formula with the correct subject.
To calculate the volume, we need to divide the mass of the object by the density of the substance.
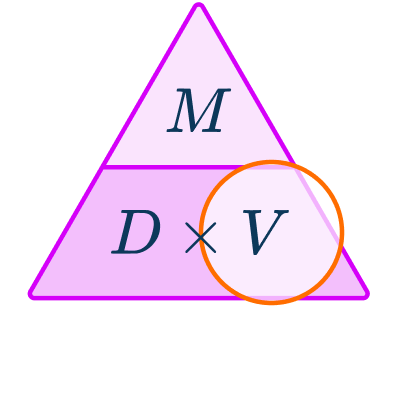
V=\cfrac{M}{D}
Substitute known values into the formula and do the calculation.
Write down the solution including the units.
Let’s look at how the units were calculated:
The units for mass here are grams \mathrm{g}.
The units for density here are grams per cubic centimeter, \mathrm{g/cm}^{3}.
As mass is divided by density to get volume, the units are
g\div\left(\mathrm{g/cm}^{3}\right)=g\div\cfrac{\mathrm{g}}{\mathrm{cm}^{3}}=\cfrac{\mathrm{g}}{1}\times\cfrac{\mathrm{cm}^{3}}{\mathrm{g}}=\mathrm{cm}^{3}
Note how the grams canceled out and left just \mathrm{cm}^3. This makes sense, because you are calculating volume, which is measured in \mathrm{cm}^3.
The volume of the object is 187.5\mathrm{~cm}^{3}.
Example 4: calculating the volume (m³)
The mass of an object is 1.5\mathrm{~kg}. The density of the substance which the object is made from is 6\mathrm{~g/m}^{3}. Calculate the volume of the object.
Write the formula with the correct subject.
To calculate the volume, divide the mass of the object by the density of the substance.

V=\cfrac{M}{D}
Substitute known values into the formula and do the calculation.
Note, here we have been given the mass in kilograms, but the density is in \mathrm{g/cm}^{3} so convert the mass to grams first.
1.5\mathrm{~kg}=1,500\mathrm{~g}
V=\cfrac{M}{D}=\cfrac{1500}{6}=250
Write down the solution including the units.
Let’s look at how the units were calculated:
The units for mass here are grams \mathrm{g}.
The units for density here are grams per cubic centimeter, \mathrm{g/cm}^{3}.
As mass is divided by density to get volume, the units are
g\div\left(\mathrm{g/cm}^{3}\right)=g\div\cfrac{\mathrm{g}}{\mathrm{cm}^{3}}=\cfrac{\mathrm{g}}{1}\times\cfrac{\mathrm{cm}^{3}}{\mathrm{g}}=\mathrm{cm}^{3}
The volume of the object is 250\mathrm{~cm}^{3}.
Example 5: calculate mass (g)
Copper has a density of 9\mathrm{~g/cm}^{3}. Calculate the mass of 240\mathrm{~cm}^{3} of copper.
Write the formula with the correct subject.
To calculate the mass, multiply the density of the substance by the volume of the object.
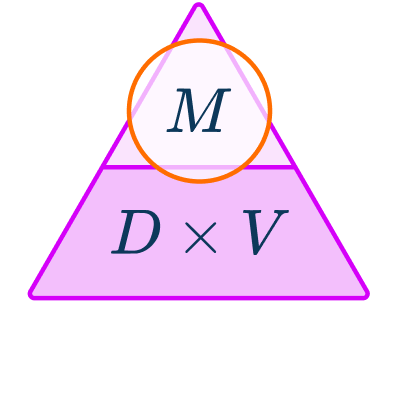
M=D\times{V}
Substitute known values into the formula and do the calculation.
Write down the solution including the units.
Let’s look at how the units were calculated.
The units for density here are grams per cubic centimeter, \mathrm{g/cm}^{3}.
The units for volume here are cubic centimeters, \mathrm{cm}^{3}.
As density is multiplied by volume to get mass, the units are
\cfrac{\mathrm{g}}{\mathrm{cm}^3}\times\mathrm{cm}^3=\cfrac{g}{\mathrm{cm}^3} \times\cfrac{\mathrm{cm}^3}{1}=g
Note how the centimeters cubed canceled out and left just \mathrm{g}. This makes sense, because you are calculating mass, which is measured in \mathrm{g}.
The mass of the object is 2,160\mathrm{~g}.
Example 6: calculating the mass (kg)
Lead has a density of 11.29\mathrm{~g/cm}^{3}. Calculate the mass of 0.5\mathrm{~m}^{3} of lead. Write your answer in kilograms.
Write the formula with the correct subject.
To calculate the mass, multiply the density of the lead by the volume of the lead.

M=D\times{V}
Substitute known values into the formula and do the calculation.
Since the volume of lead is 0.5\mathrm{~m}^{3} and the density is 11\mathrm{~g/cm}^{3}, convert the volume to \mathrm{cm}^{3} so they have the same unit.
1\mathrm{~m}^{3}=1,000,000\mathrm{~cm}^{3}
This means that 0.5\mathrm{~m}^{3}=500,000\mathrm{~cm}^{3}.
M=D\times{V}=11.29\times{500,000}=5,645,000
Write down the solution including the units.
Let’s look at how the units were calculated.
As density is multiplied by volume to get mass, the units are
\cfrac{\mathrm{g}}{\mathrm{cm}^3}\times\mathrm{cm}^3=\cfrac{g}{\mathrm{cm}^3} \times\cfrac{\mathrm{cm}^3}{1}=g
The mass is 5,645,000\mathrm{~g} but the question asked for the answer in kilograms.
As 1\mathrm{~kg}=1,000\mathrm{~g},
5,645,000\mathrm{~g}=5,645\mathrm{~kg}
The mass of the object is 5,645\mathrm{~kg}.
Teaching tips for density mass volume triangle
- Have a unit conversion chart posted in the classroom for students to refer to.
- Remind students that the unit of volume can be a capacity unit, like gallons, but it can also be a mathematical unit like \mathrm{cm}^3.
- Let students experience density hands on, instead of only using practice problems worksheets. This can be as simple as pouring different liquids into the same container, observing what happens and making conjectures about the density of substances in the container.
- Have students copy a few example problems for them to refer to as they answer practice questions on their own.
- Since the focus of this skill is understanding the formula and the units, let struggling students use a density calculator until they are comfortable completing the calculations on their own.
Easy mistakes to make
- Forgetting how to find the volume
You may need to find the volume of an object first. Remember, the volume of a rectangular prism is the product of its three dimensions.
For example,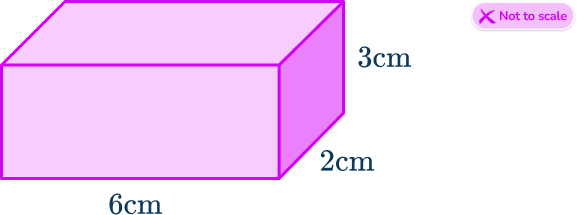
\text{Volume}=6\times{3}\times{2}=36\mathrm{cm}^{3}
- Confusing the conversions of measurement
Metric units are often used for mass, density and volume. It’s important to know how to convert between metric units.
For example, knowing there are 100\mathrm{~cm} in 1\mathrm{~m}.
- Not paying attention to what the question is asking
Check that you give the answer in the right form. You may have solved grams, but the answer needs to be in kilograms. You may have an answer which needs to be rounded to a specific number of significant figures or decimal places.
Related compound measures lessons
Practice density mass volume questions
1. Calculate the density of an object with a mass of 300\mathrm{~g} and a volume of 150\mathrm{~cm}^{3}.




2. Calculate the density of an object when the volume is 450\mathrm{~cm}^{3} and its mass is 700\mathrm{~g}. Give your answer to 3 significant figures.




D=\cfrac{M}{V}=\cfrac{700\mathrm{~g}}{450\mathrm{~cm}^{3}}=1.555 \ldots=1.56\mathrm{~g/cm}^{3} (rounded to the nearest hundredth)
3. Calculate the volume of an object when the mass of the object is 400\mathrm{~g} and the density of the substance is 16\mathrm{~g/cm}^{3}.




Let’s look at how the units were calculated.
\cfrac{\mathrm{g}}{\mathrm{g/cm}^{3}}=g\div\cfrac{\mathrm{g}}{\mathrm{~cm}^3}=\cfrac{\mathrm{g}}{1}\times\cfrac{\mathrm{cm}^3}{\mathrm{g}}=\mathrm{cm}^3
Note how the grams canceled out and left just \mathrm{cm}^{3}. This makes sense, because you are calculating volume, which is measured in \mathrm{cm}^{3}.
4. Calculate the volume of an object when the density of the substance is 13\mathrm{~g/cm}^{3} and its mass is 0.85\mathrm{~kg}. Write your answer to 3 significant figures.




Converting the mass to grams, 0.85\mathrm{~kg}=850\mathrm{~g}.
V=\cfrac{M}{D}=\cfrac{850\mathrm{~g}}{13\mathrm{~g/cm}^{3}}=65.384\ldots=65.4\mathrm{~cm}^{3} (rounded to the nearest tenth)
5. The density of a substance is 12\mathrm{~g/ml} and its volume is 360\mathrm{~ml}. Calculate the amount of mass of the substance in \mathrm{kg}.




Let’s look at how the units were calculated.
\cfrac{\mathrm{g}}{\mathrm{cm}^{3}}\times\mathrm{cm}^{3}=\cfrac{g}{\mathrm{cm}^{3}}\times\cfrac{\mathrm{cm}^{3}}{1}=\mathrm{g}
Note how the centimeters cubed canceled out and left just \mathrm{g}. This makes sense, because you are calculating mass, which is measured in \mathrm{g}.
The question asks for the answer in \mathrm{kg} so to convert grams to kilograms, divide by 1,000 to get:
4,320\mathrm{~g}=4.32\mathrm{~kg}
6. The density of this rectangular prism is 15\mathrm{~g/cm}^{3}. Calculate the mass of the rectangular prism.
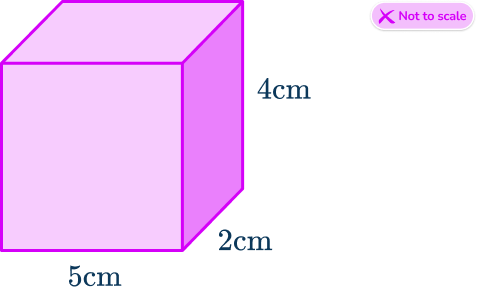




First, calculate the volume of the rectangular prism.
\text{Volume}=5\times{4}\times{2}=40\mathrm{~cm}^3
The mass is calculated by multiplying the density by the volume.
M=D\times{V}=15\mathrm{~g/cm}^{3}\times40\mathrm{~cm}^3=600\mathrm{~g}
Density mass volume triangle FAQs
A cuboid is another name for a rectangular prism.
The density formula is \rho=\cfrac{m}{V}, and \rho is density, m is mass and V is volume.
The next lessons are
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!