High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Fractions Decimals Coordinate plane Linear graph Congruence and similarityTransformations
Here you will learn about transformations, reflections, translations, rotations and dilations.
Students will first learn about transformations as part of geometry in 7 th and 8 th grade and continue to learn about them in high school.
What are transformations?
Transformations change the size and/or the position of a shape.
The first type of transformation students are introduced to in school is usually scale factor. The scale factor describes how much the size of a shape has been scaled up or down.
The scale factor is multiplied by every side length of a shape to increase or decrease the size. Changing a shape by a scale factor greater than \bf{1} will make the shape a larger figure.
For example,
Shape A that has been enlarged by scale factor 2 to give shape B.
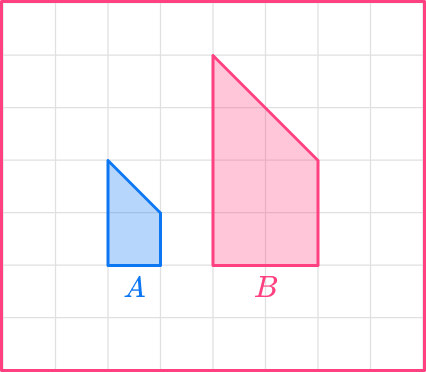
Step-by-step guide: Scale factor
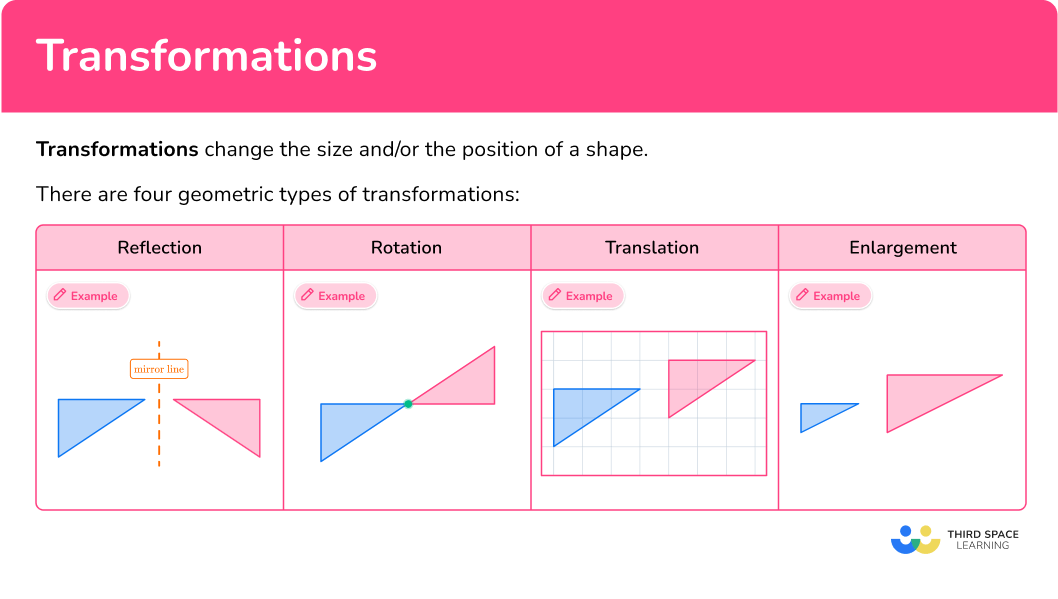
There are four geometric types of transformations:
Rotations involve a center of rotation, an angle of rotation and a direction of rotation (clockwise or anticlockwise).
For example,
Rotate shape A 90^{\circ} clockwise around a fixed point.
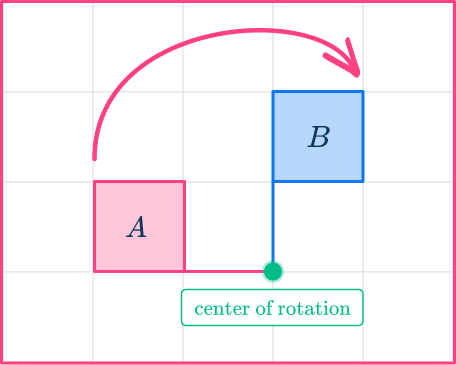
Shape A has been rotated a quarter turn clockwise to give shape B.
Step-by-step guide: Rotations
Translations involve a horizontal shift or vertical shift.
For example,
Shape A has been translated to shape B by the column vector \begin{pmatrix} \; 3 \;\\ \; 2 \; \end{pmatrix}
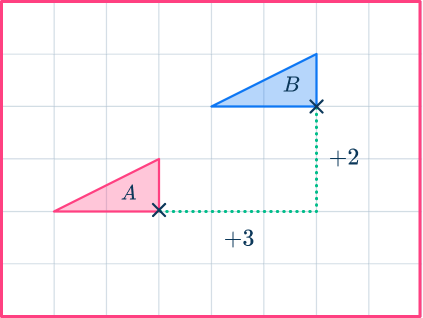
Step-by-step guide: Translation math
Reflections involve a mirror line, also known as a line of reflection.
For example,
Triangle P has been reflected across the line x=4 to give Triangle Q.
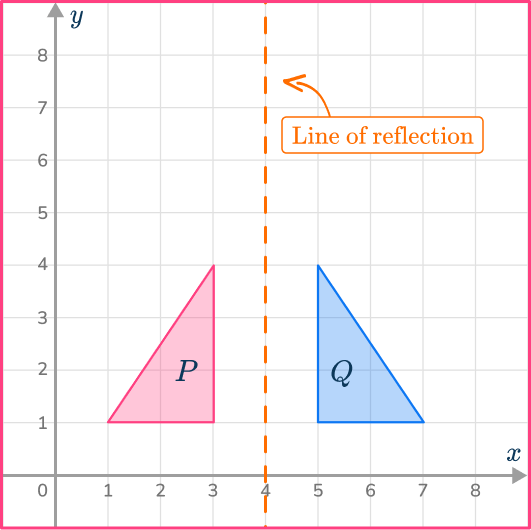
Triangle P is the original shape and Triangle Q is the image.
Step-by-step guide: Reflection in math
Dilations make a shape bigger or smaller. They must have a scale factor and they may involve a center of enlargement.
For example,
Shape A has been reduced by scale factor \cfrac{1}{2} to make shape B.
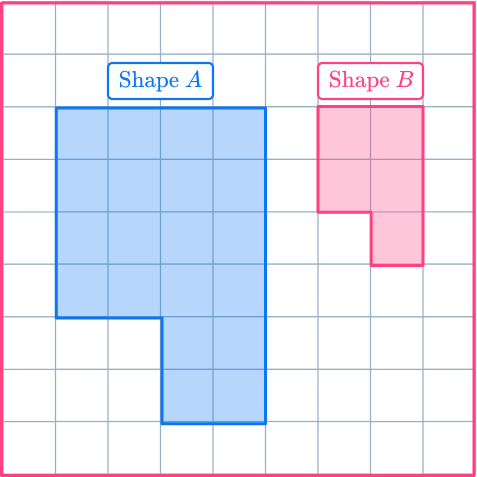
The corresponding angles are identical but the length of each side in shape B is half the size of the original shape.
Step-by-step guide: Dilations
The center of dilation is the fixed point from which all points of a figure are scaled during a dilation. To apply a dilation, draw rays from the center of dilation through the vertices of the original shape. These lines guide the resizing process.
For example,
Here triangle ABC has been enlarged by scale factor 2 about a center of dilation point O. The new triangle is A’B’C’.
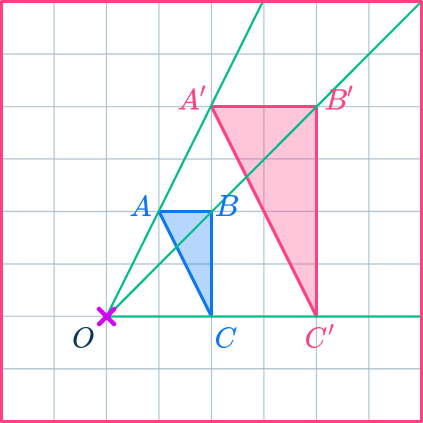
The lengths of the sides of the dilated image are double the lengths of the sides of the original shape.
The pairs of corresponding sides are parallel lines.
Step-by-step guide: Center of dilation
What are transformations?
Common Core State Standards
How does this relate to 7 th grade math, 8 th grade math and high school math?
- Grade 7 – Geometry (7.G.A.1)
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
- Grade 8 – Geometry (8.G.A.3)
Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- High School – Geometry – Congruence (HS.G.CO.A.5)
Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, for example, graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
- High School – Geometry – Congruence (HS.G.CO.B.6)
Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
- High school – Geometry – Similarity, Right Triangles, and Trigonometry (HSG.SRT.A.1)
Verify experimentally the properties of dilations given by a center and a scale factor.
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.A.1a)
A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged.
- High School – Geometry – Similarity, Right Triangles, & Trigonometry (HS.G.SRT.A.1b)
The dilation of a line segment is longer or shorter in the ratio given by the scale factor.
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREE![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
[FREE] Common Core Practice Tests (Grades 3 to 8)
![[FREE] Common Core Practice Tests (Grades 3 to 8)](https://thirdspacelearning.com/wp-content/uploads/2023/10/Common-Core-Practice-Test-Grade-3-8-OG-Image.png)
Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
DOWNLOAD FREEHow to perform transformations
In order to perform transformations:
- Identify the transformation required.
- Complete the transformation.
Transformations examples
Example 1: using a scale factor to enlarge a shape
Enlarge this shape by scale factor 3 \text{:}
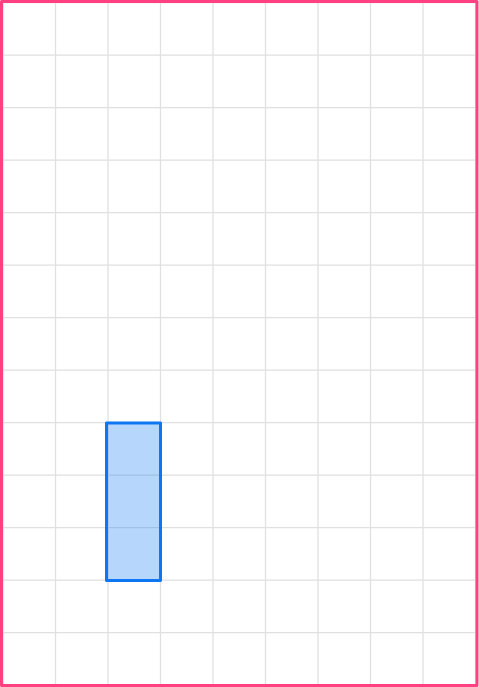
- Identify the transformation required.
This will be a dilation using scale factor. This is where you shrink or enlarge a shape; the dimensions change, but the orientation of the shape stays the same.
2Complete the transformation.
Let’s start with the base. The base in the original shape is 1, so the base of the image will be 3.
1\times3=3You can draw it anywhere on the grid.
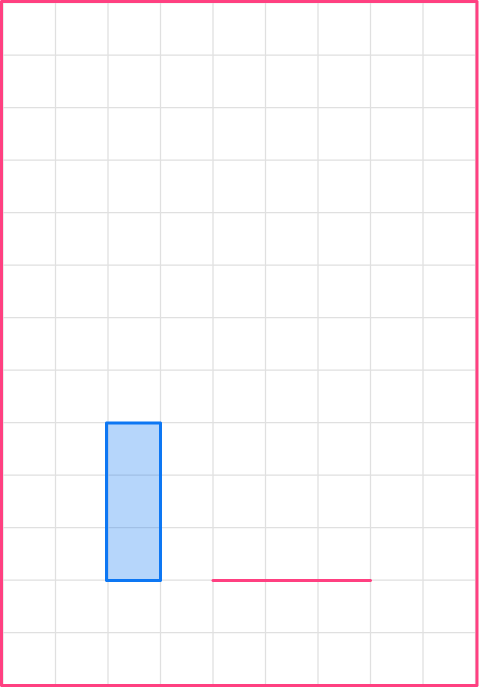
Now let’s do the height. The height of the first shape is 3, so the height of the enlarged shape will be 9.
3\times3=9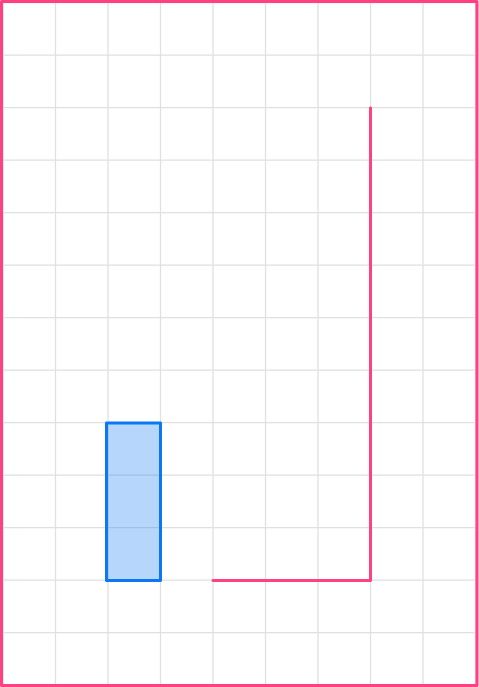
Now, complete the scaled shape.
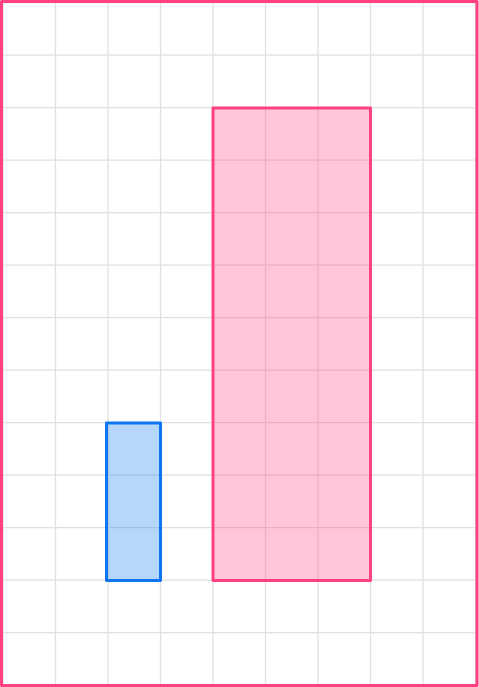
The lengths of the sides of the image are triple the lengths of the preimage. You can see the different sizes of the shapes above.
Example 2: rotate a shape around a center of rotation
Rotate the shape 180^{\circ} about the origin.
Identify the transformation required.
The question says to “rotate the shape”, which is a rotation. This is where you turn the shape about a point; the dimensions stay the same, but the orientation and the location of the shape changes.
Complete the transformation.
Mark the center of rotation on the diagram. The origin of the coordinate grid is the coordinates (0,0). It can be useful to add a line on the diagram extending from the shape to the center of rotation.
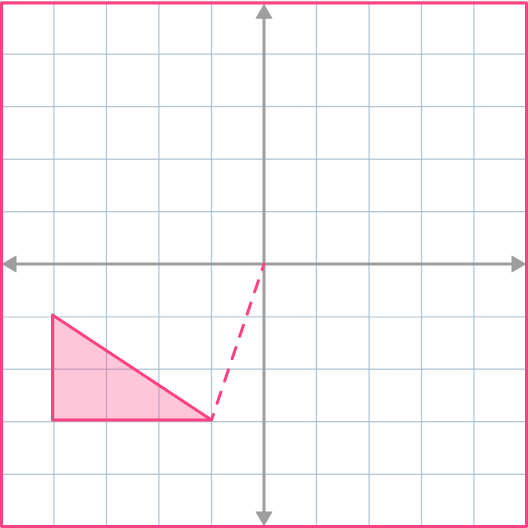
360^{\circ} is a full rotation so 180^{\circ} is half rotation. Rotate the shape halfway around the origin.
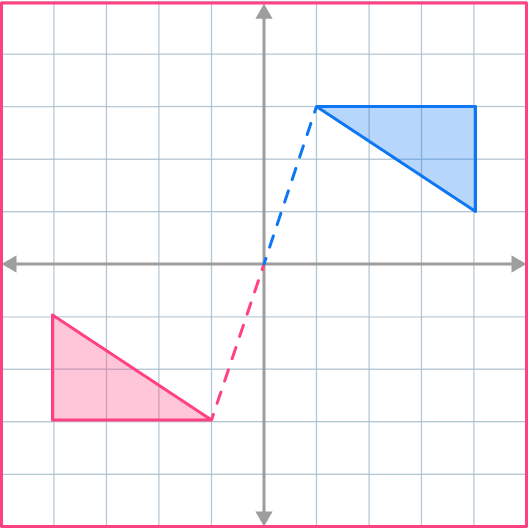
Notice how the additional dotted lines form a straight line or a 180^{\circ} angle.
Example 3: translate a 2D shape
Translate shape A by the column vector \begin{pmatrix} \; 0 \;\\ \; -3 \; \end{pmatrix} and label the image B.
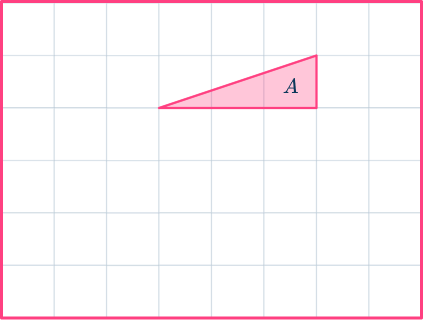
Identify the transformation required.
The question says to “translate the shape”, which is a translation. This is where you shift the shape up/down or left/right; the dimensions and orientation stay the same, but the location of the shape changes.
Complete the transformation.
Choose one of the vertices of the shape as the point you are going to move. Let’s use the bottom left hand corner of the shape.
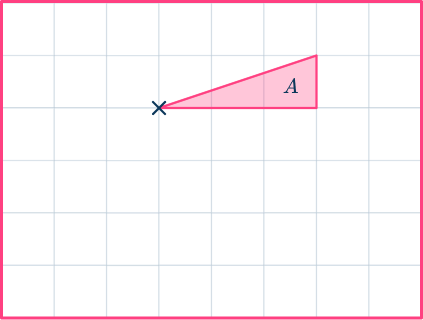
The top number in the column vector is 0 , so there is no horizontal movement of the point.
The bottom number in the column vector is -3 , so move the point 3 units down.
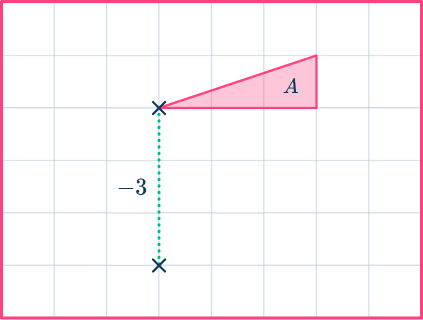
Move each of the other vertices in the same way and draw in the rest of the 2D shape.
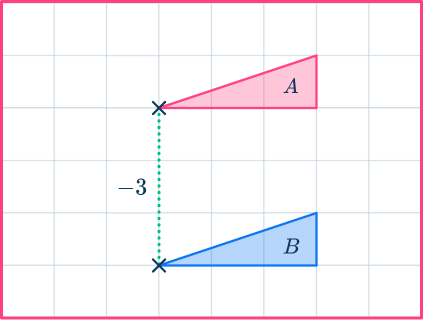
Example 4: reflect a shape on a coordinate grid
Reflect the triangle across the line y=-1\text{.}
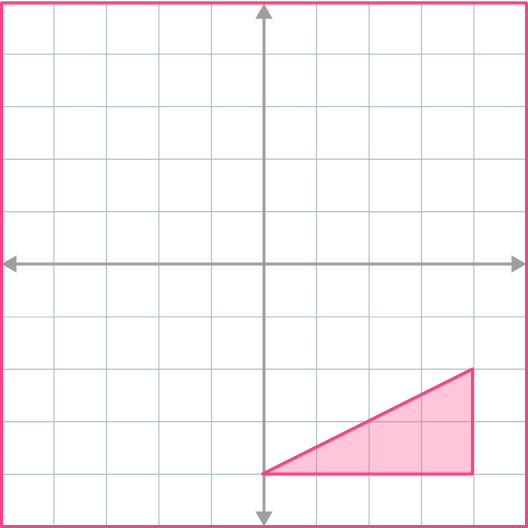
Identify the transformation required.
The question says to “reflect the triangle”, which is a reflection. This is where you flip the shape across a line, creating a mirror image; the dimensions stay the same, but the orientation and location of the shape changes.
Complete the transformation.
The line of reflection is y=-1 (the mirror line). This is a horizontal line that intersects the y- axis at -1. Draw this on the diagram.
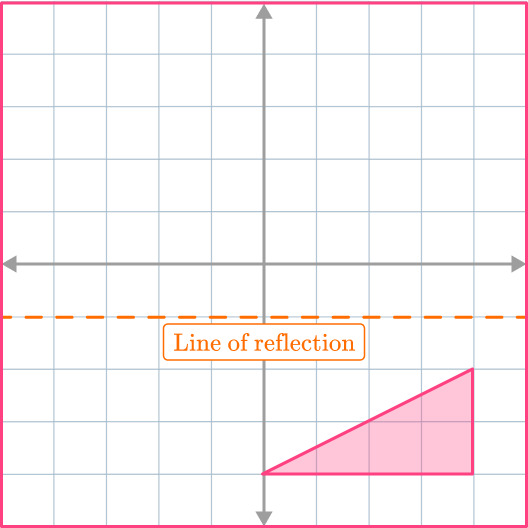
Choose the first vertex to reflect. It is easier to start with a vertex which is closest to the line of reflection (the mirror line). Let’s reflect the vertex (4, -2). The new vertex will be exactly the same distance away from the line of reflection as the original vertex.
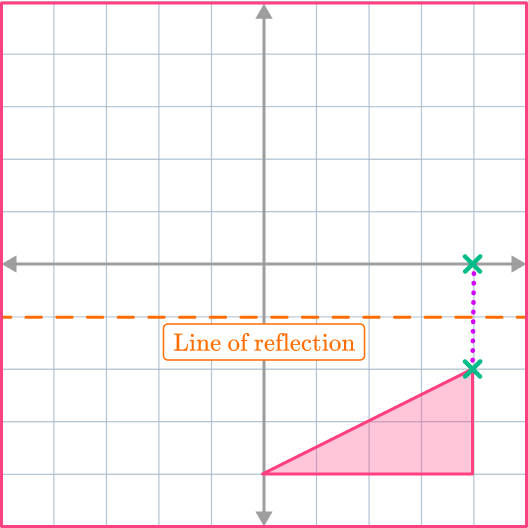
Here the second vertex (0, 4) is being reflected to give its image.
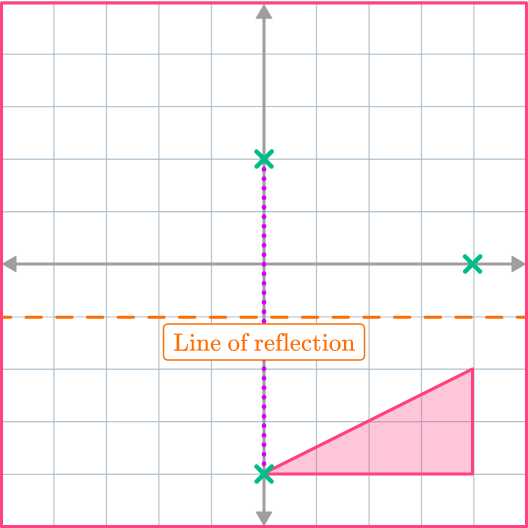
You can then reflect the third vertex (4, -4).
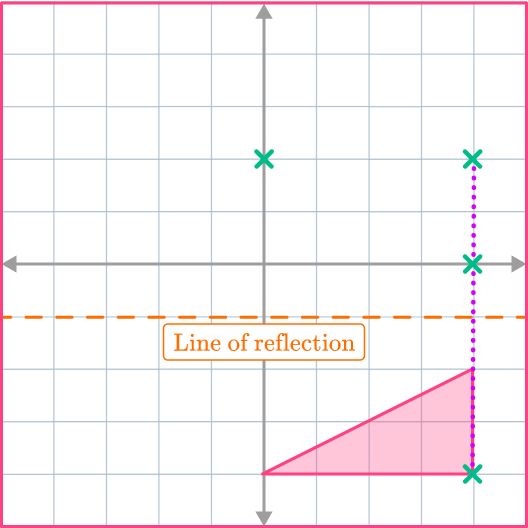
To finish the diagram, join up the reflected vertices.
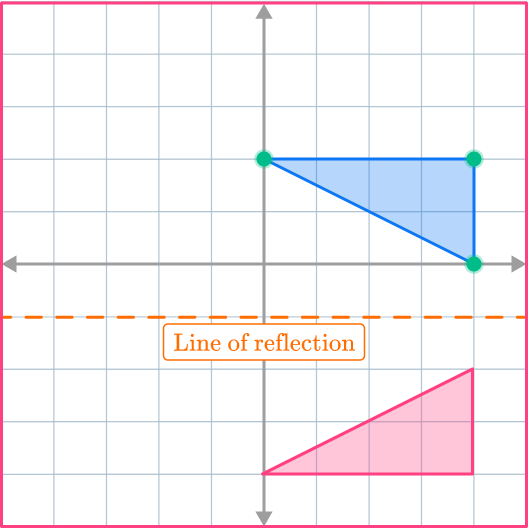
Example 5: dilation on a coordinate plane
Enlarge the shaded shape by scale factor 2 about the point (1,1) .
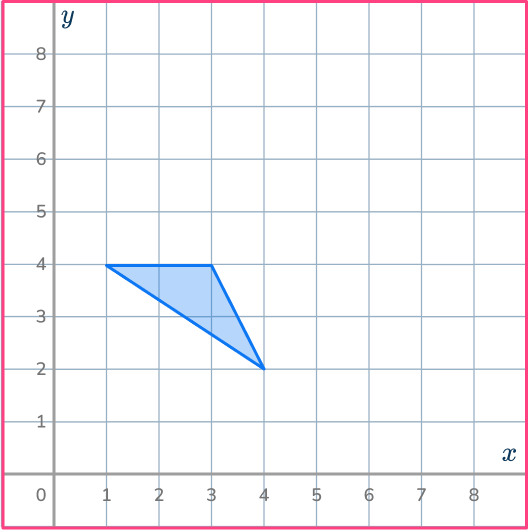
Identify the transformation required.
This will be a dilation on the coordinate grid using scale factor. This is where you shrink or enlarge a shape; the dimensions and location change, but the orientation of the shape stays the same.
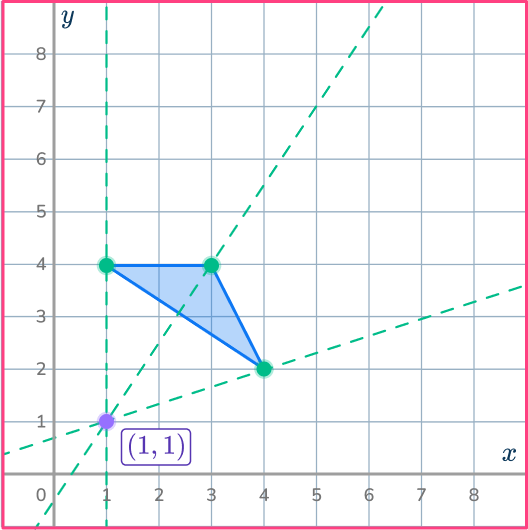
Complete the transformation.
Draw a dilation image using a scale factor of 2. This means each side length of the dilation image will be 2 times as long as the corresponding side length of the original shape.
First, you’ll need to plot the center of dilation on the coordinate grid. Then draw three ray lines from the center of dilation through the three vertices of the original shape.
Use the ray lines to help you enlarge the shape.
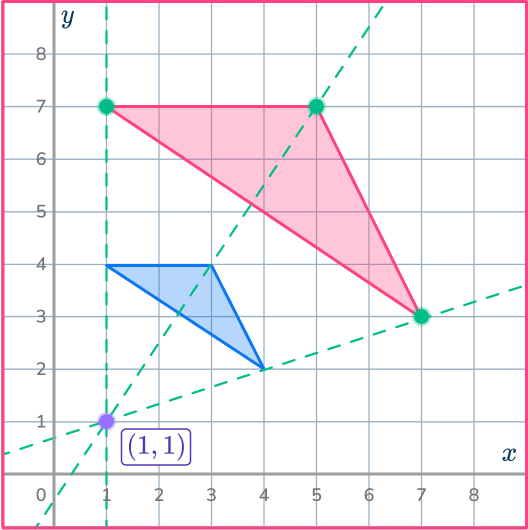
Example 6: dilation on a coordinate plane
Shrink the shaded shape by scale factor \cfrac{1}{2} about the point (1,0).
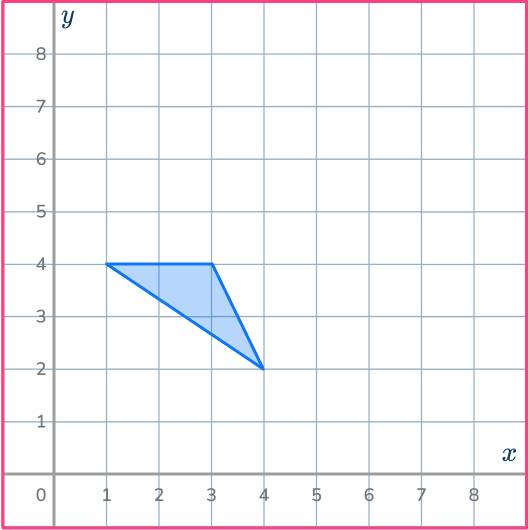
Identify the transformation required.
This will be a dilation on the coordinate grid using scale factor. This is where you shrink or enlarge a shape; the dimensions and location change, but the orientation of the shape stays the same.
Complete the transformation.
Draw a dilation image using a scale factor of \cfrac{1}{2}. This means each side length of the dilation image will be \cfrac{1}{2} times as long as the corresponding side length of the original shape.
First, you’ll need to plot the center of dilation on the coordinate grid. Then draw three ray lines from the center of dilation through the three vertices of the original shape.
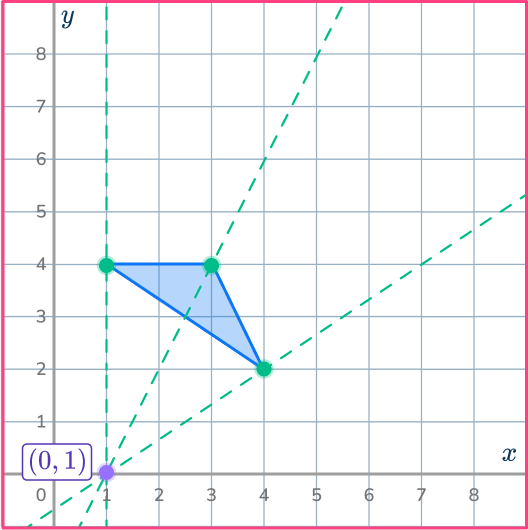
Use the ray lines to help you shrink the shape.
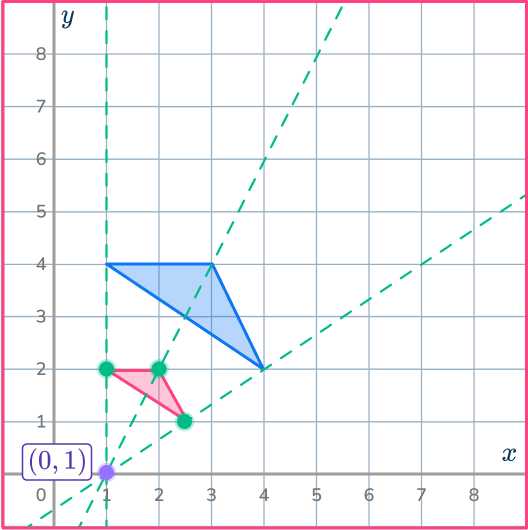
Teaching tips for transformations
- A good intro into this topic is to give students definitions of transformations and simple 2D shapes, preferable triangles or quadrilaterals, to practice with.
In the beginning, using digital tools or tracing paper, so that students can easily transform figures and make sense of each type of transformation.
- Rotations and dilations not centered on the origin are typically the hardest transformation for students to learn to do without tools.
As students are learning how to perform rotations with digital tools or tracing paper, highlight key strategies that will help them problem-solve when such tools are not available.
In particular, notice the use of guiding lines in the examples and explanations on this page, for these types of transformations.
Easy mistakes to make
- Not using the grid to help put the vertices of the shape in the correct position
Geometric transformations of shapes are often on grid paper. Use the lines and squares on the grid to help you be accurate about the position of the new shape.
- Not adding extra details onto your diagram to help you
Try not to do transformation work in your head. Make use of your pencil and ruler to add marks to help you. You may also use tracing paper (thin paper that you can see through).
- Forgetting to describe transformations fully
When you are asked to describe a transformation, make sure you state which kind of transformation it is and all other details.
- Not making sure you have the object and the image the right way around
The original shape is the preimage and the translated shape is the image. Make sure you know which shape is the original shape and start there when describing transformations such as translations.
- Confusing the \textbf{x}- axis and \textbf{y}- axis when completing reflections
Remember that the x- axis runs horizontal and the y- axis runs vertical. Confusing these can lead to incorrect reflections.
Practice transformations questions
1. Enlarge this shape by a scale factor of 2.



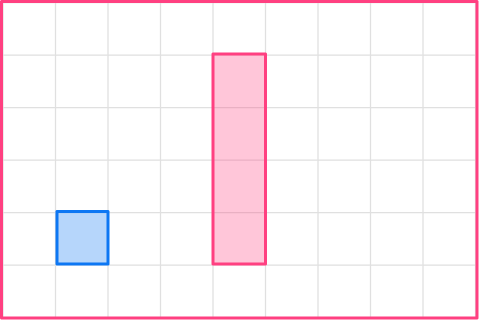

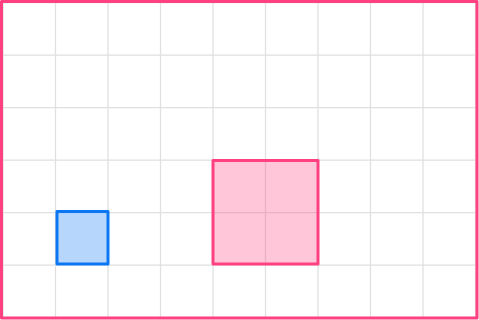

Scale factor involves multiplying all sides of the shape by the same number to shrink or enlarge it. In this case, since the scale factor is 2, the shape will be enlarged.
1 \times 2=2
The enlargement will be a square with side length 2.
2. Rotate the shaded shape 90^{\circ} clockwise around (0,0)\text{.}
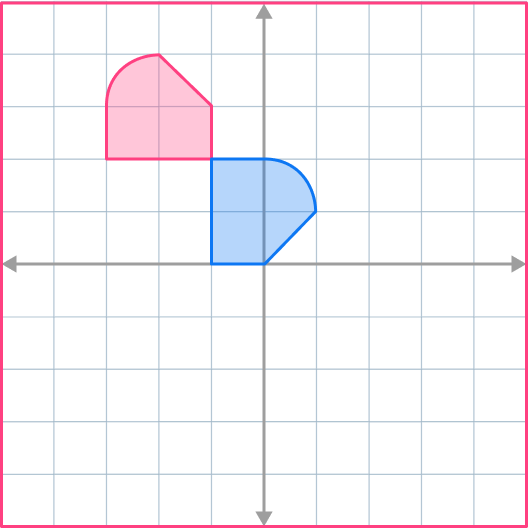




The shape has to be rotated 90^{\circ} clockwise. The center of rotation should be the origin.
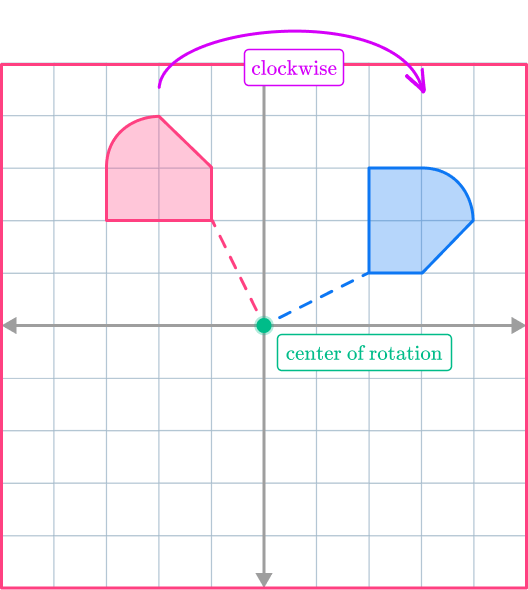
As you can see, the shape starts in the 2 nd quadrant but the rotated image is in the 1 st quadrant (having rotated across the y- axis.) Notice how the additional dotted lines form a 90^{\circ} angle.
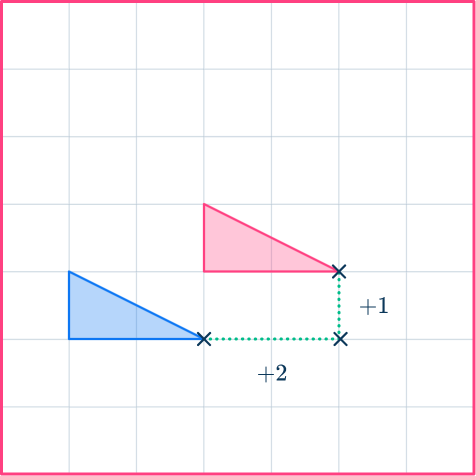
3. Translate the shaded shape by the column vector \begin{pmatrix} \; 2 \;\\ \; 1 \; \end{pmatrix} .
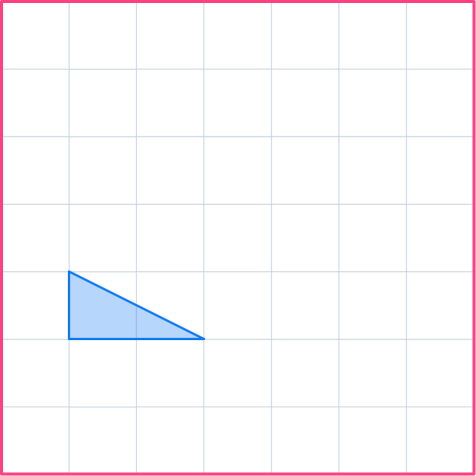
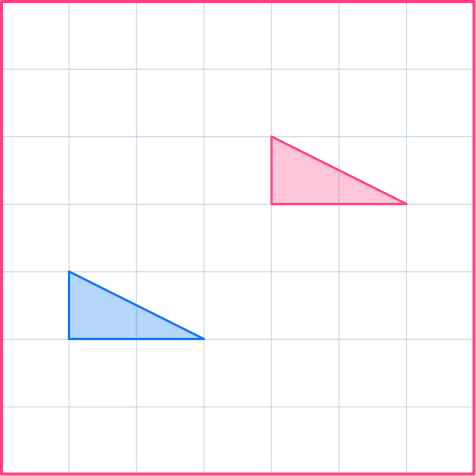

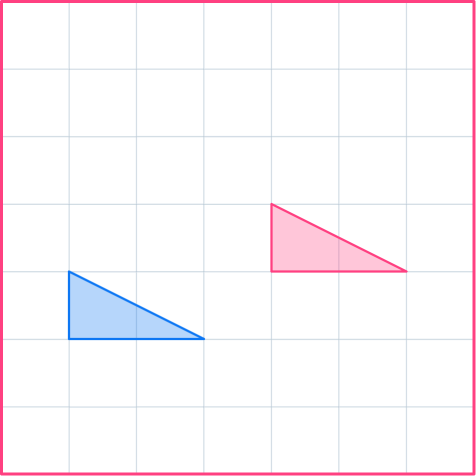

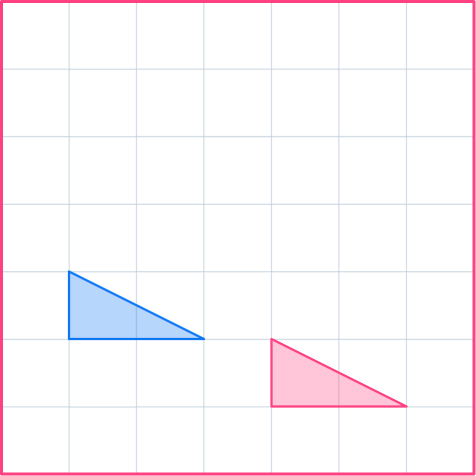

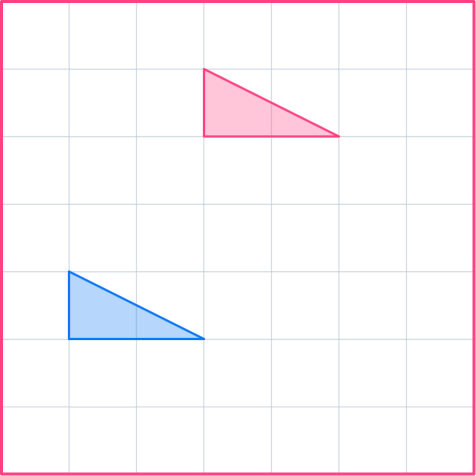

Choose a point on the vertex of the shape and move it 2 to the right and 1 up. Do the same with all the points, or carefully draw in the rest of the image.
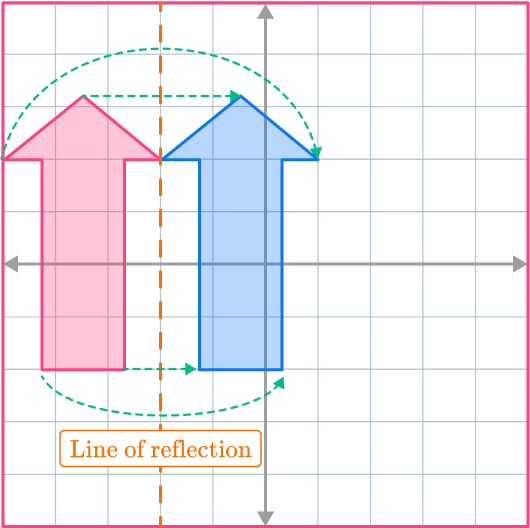
4. Reflect the shape across x=-2.
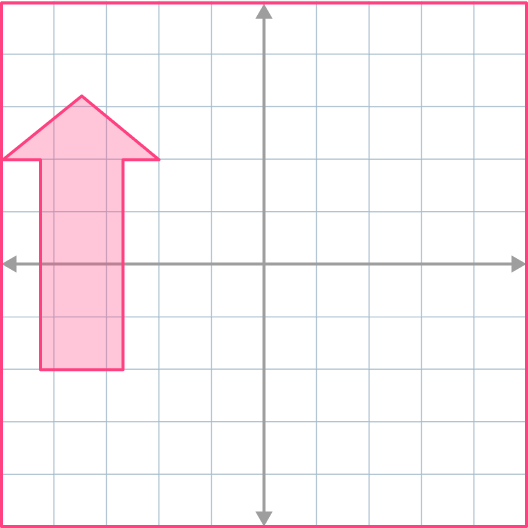
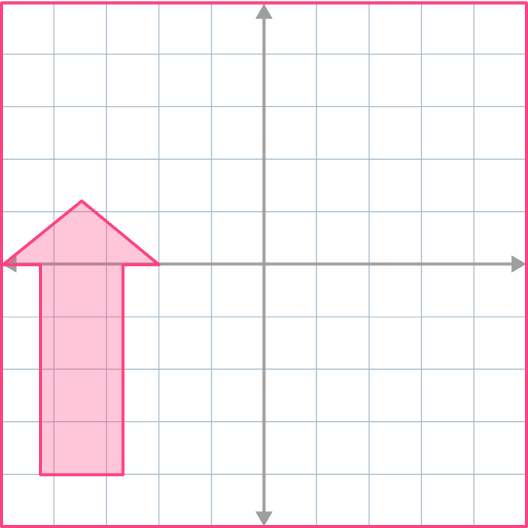

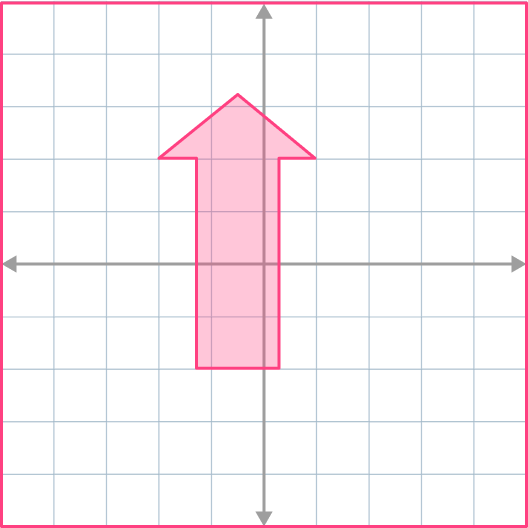

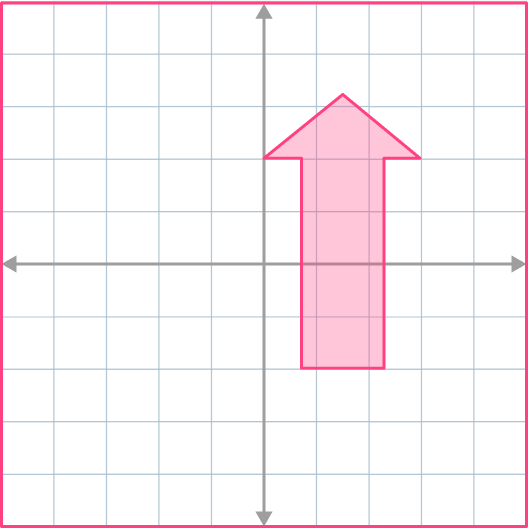

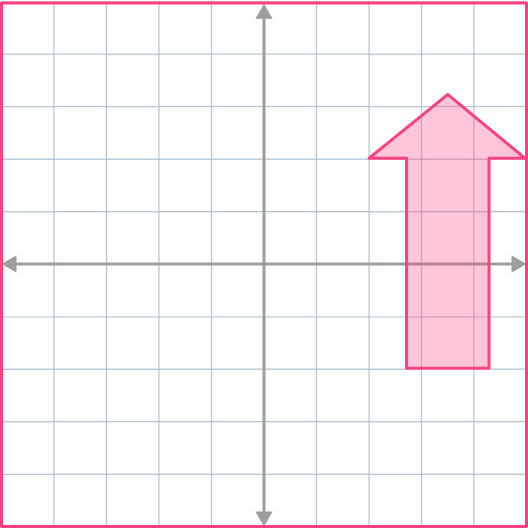

The corresponding points on the object and the image must be equidistant (the same distance) from the line of reflection.
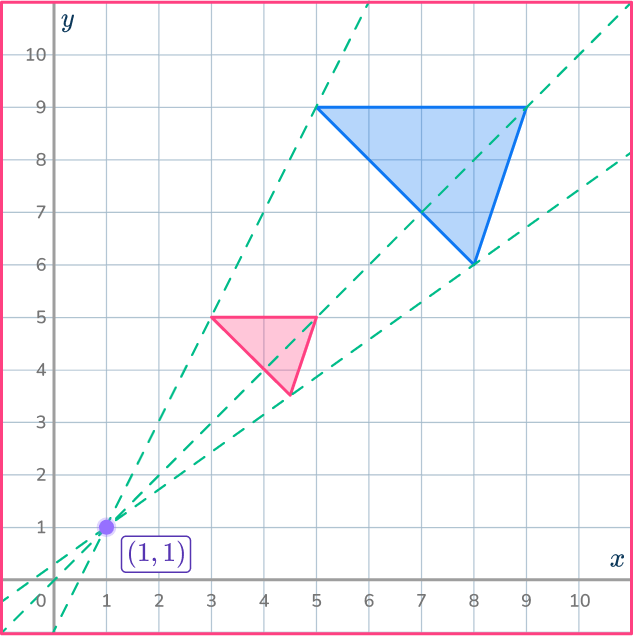
5. Dilate the shaded shape with scale factor \cfrac{1}{2} about the point (1,1).
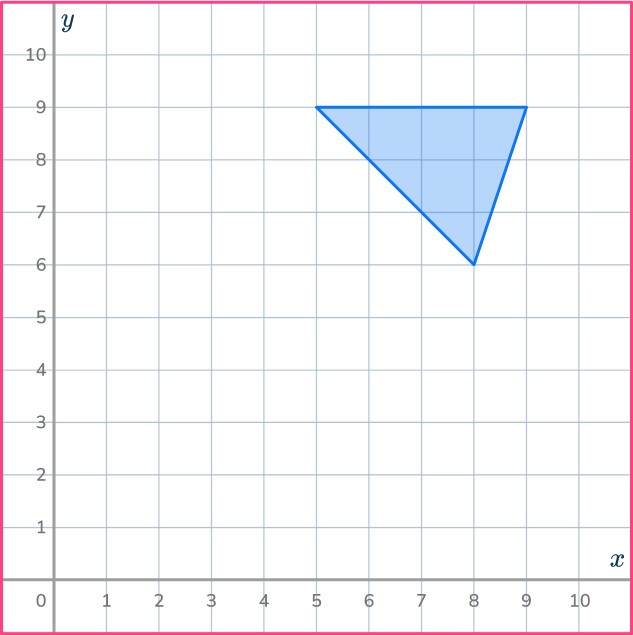
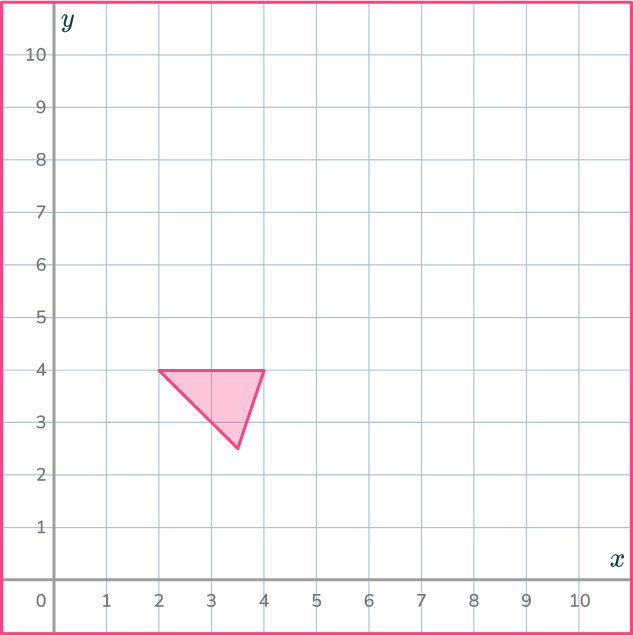

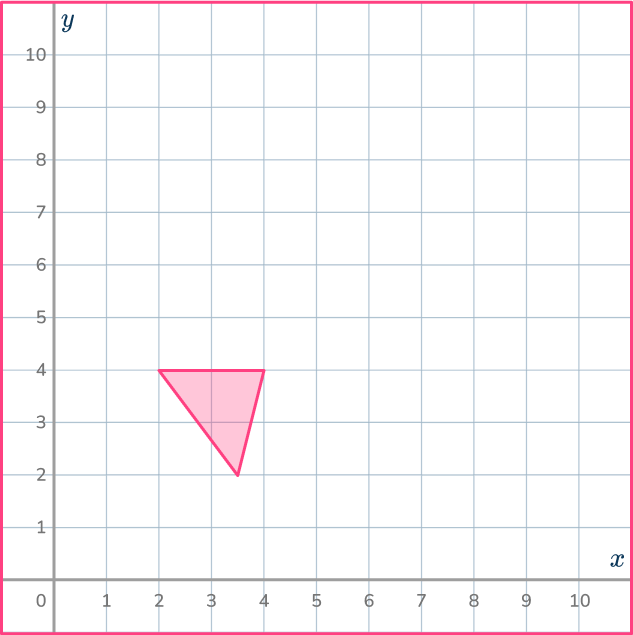

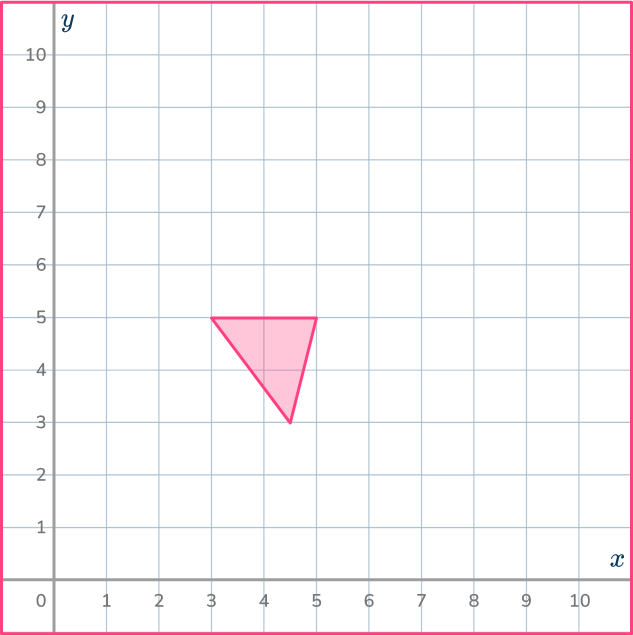

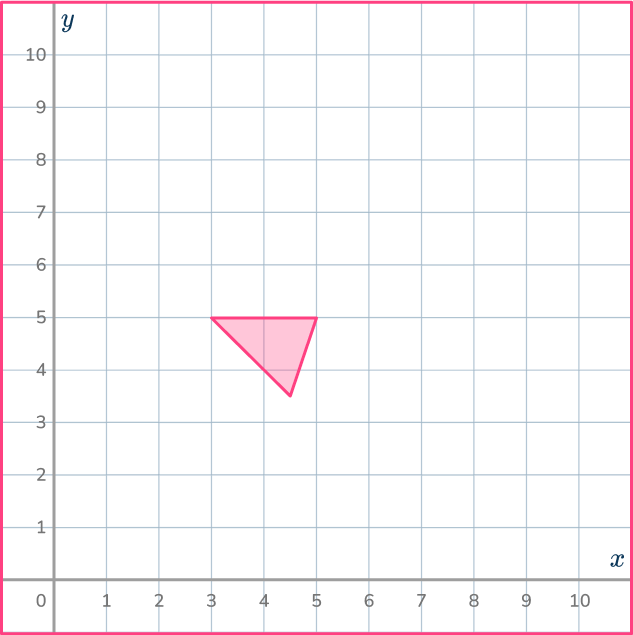

Use the ray lines to help you shrink the shape by \cfrac{1}{2} and get it in the correct position.
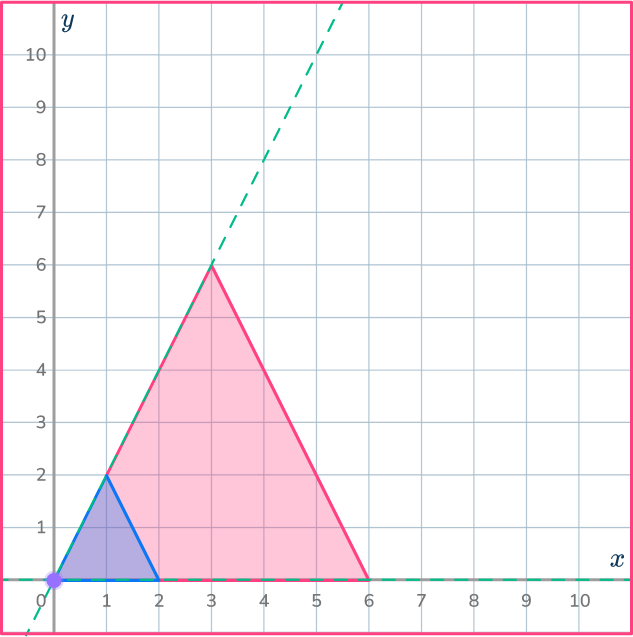
6. Dilate the shaded shape with scale factor 3 about the origin.
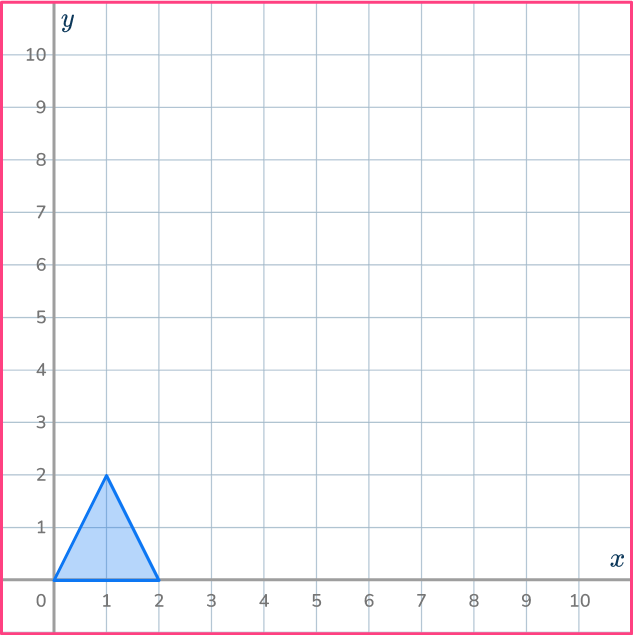
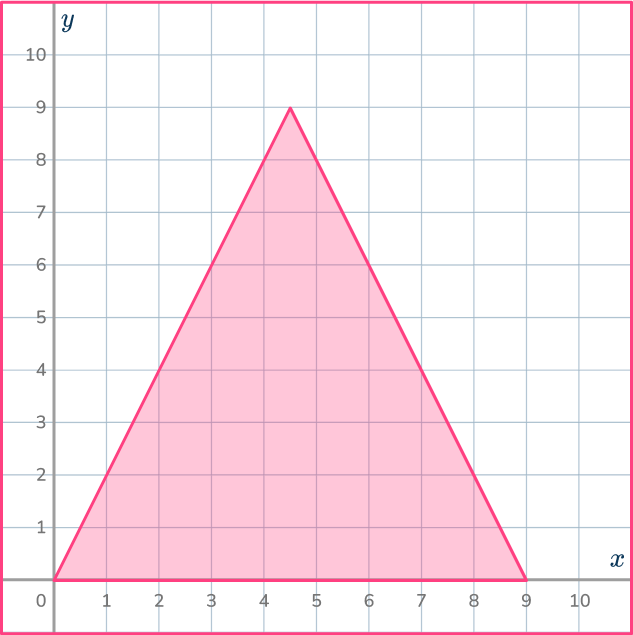

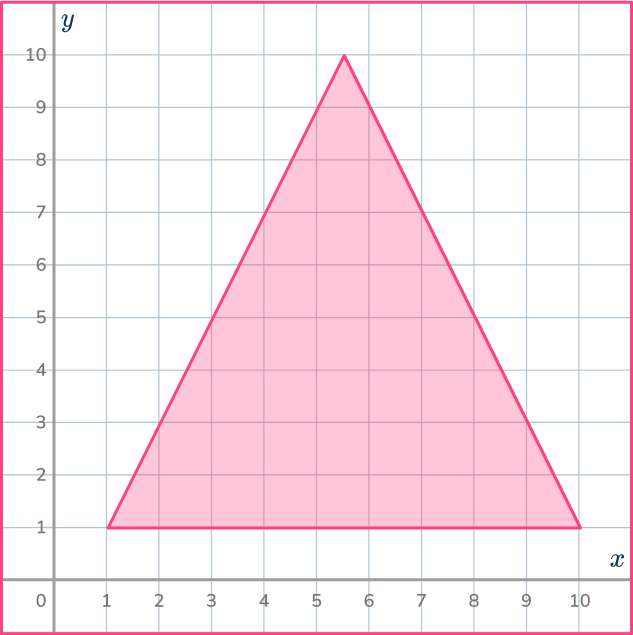




Use the ray lines to help you shrink the shape by 3 and get it in the correct position.
Transformation FAQs
A transformation that does not change the dimensions of the figure.
A function with a variable with an exponent of 2, that is the highest degree of any variables in the function.
It is the distance that number is from 0.
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!