[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

DOWNLOAD FREE

In order to access this I need to be confident with:

2D shapes Irrational numbers Rounding decimals Area Surface area

Math resources Geometry

Circle math

Pi r squared

𝝅r² (pi r squared)

Here you will learn about using the formula $\boldsymbol{\pi} r^2 \text { (pi r squared) }$ to calculate the area of a circle given the radius, diameter, or circumference.

Students will first learn about $\boldsymbol{\pi} r^2 \text { (pi r squared) }$ as part of geometry in $7$ th grade.

What is pi r squared?

Pi r squared (pi times the radius squared) is the formula for the area of a circle.

This is because there is a specific relationship between the radius of a circle and its area.

Area of a circle formula:

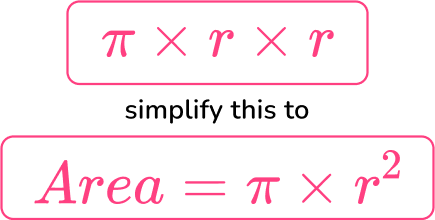
For example,

What is the area of a circle with radius $5 \, cm?$ Give your answer to the nearest tenth.

Squaring the radius of $5$ gives $25.$ Then multiply pi by this value to find the area of the circle.

\begin{aligned}\text { Area } & =\pi r^2 \\\\ & =\pi \times 5^2 \\\\ & =25 \pi \mathrm{~cm}^2 \\\\ & =78.5 \mathrm{~cm}^2 \text { (to the nearest tenth) }\end{aligned}

What is pi?

$\pi$ (pronounced pi) is a Greek letter that represents the ratio of the circumference of a circle to its diameter.

For all circles, if you divide the length of the circumference by the length of the diameter you get the value $\boldsymbol{\pi}.$

Note: $\boldsymbol{\pi}$ is an irrational number which means it cannot be written as a fraction. It is a non-recurring decimal and has an approximate value of $3.1415\dots$

Sometimes the question may ask you to give the answer ‘in terms of $\pi$ ’.

For example,

$3 \times \pi = 3\boldsymbol{\pi}$ (this is an answer in terms of pi)

$5 \times \pi = 5\boldsymbol{\pi}$ (this is an answer in terms of pi)

$17 \times \boldsymbol{\pi} = 53.407…$ (this is an answer not in terms of pi)

What is pi r squared?

Common Core State Standards

How does this relate to $7$ th grade math?

Grade 7 – Geometry (7.G.B.4)
Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

DOWNLOAD FREE

[FREE] Common Core Practice Tests (Grades 3 to 6)

DOWNLOAD FREE

How to use pi r squared

In order to calculate the area of a circle:

Find the radius of the circle.
Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.
Give your answer clearly with the correct units.

Pi r squared examples

Example 1: calculating the area of the circle given the radius

A circle has a radius of $7 \, cm.$

Calculate its area.

Give your answer to the nearest hundredth.

Find the radius of the circle.

The radius is given in the question.

Radius $=7 \, cm$

2Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times7\times 7 \\\\ &49\pi \\\\ &= 153.93904\dots \end{aligned}

Remember, the question asks you to round your answer to the nearest hundredth.
$153.94$

3Give your answer clearly with the correct units.

153.94 \, cm^2

Example 2: calculating the area of the circle given the diameter

The diameter of a circle is $20 \, mm.$

Calculate its area.

Give your answer to the nearest tenth.

Find the radius of the circle.

The question gives you the diameter which is twice the radius.

Diameter $=20 \, mm$

Radius $=20 \mathrm{~mm} \div 2$

Radius $=10 \, mm$

Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times10\times 10 \\\\ &100\pi \\\\ &= 314.159\dots \end{aligned}

Remember, the question asks you to round your answer to the nearest tenth.
$314.2$

Give your answer clearly with the correct units.

314.2 \, mm^2

Example 3: calculating the area of the circle, given the radius, answer in terms of π.

A circle has a radius of $18 \, m.$

Calculate its area.

Give your answer in terms of $\pi.$

Find the radius of the circle.

The radius is given in the question.

Radius $=18 \, m$

Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times18\times 18 \\\\ &324\pi \end{aligned}

Remember, the question asks you to give your answer ‘in terms of $\pi$ ’. Therefore, you leave the answer in the form $324\pi.$

Give your answer clearly with the correct units.

324\pi \, m^2

Example 4: calculating the area of the circle given the diameter

A circle has a diameter of $210 \, km.$

Calculate its area.

Give your answer in terms of $\pi.$

Find the radius of the circle.

The question gives you the diameter which is twice the radius.

Diameter $=210 \mathrm{~km}$

Radius $=210 \mathrm{~km} \div 2$

Radius $=105 \mathrm{~km}$

Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times105\times 105 \\\\ &11025\pi \end{aligned}

Remember, the question asks you to give your answer ‘in terms of $\pi$ ’. Therefore, you leave the answer in the form $11025\pi.$

Give your answer clearly with the correct units.

11025\pi \, m^2

Example 5: calculating the area of the circle given the circumference of a circle

A circle has a circumference of $12 \, cm.$

Calculate its area.

Give your answer to the nearest hundredth.

Find the radius of the circle.

The question gives you the circumference of the circle which is equal to $2\pi r.$

This means you can find the radius of the circle from the circumference; see below:

$Circumference =2\pi r$

$Circumference =12$

$12= 2\pi r \hspace{1cm}$ Divide both sides by $2\pi$

$\cfrac{12}{2\pi}= r$

$1.9099=r$

Notice how $r$ has been rounded to more decimal places than the question requires, so you do not cause a rounding error.

Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times1.9099\times 1.9099 \\\\ &11.4596 \end{aligned}

Remember, the question asks you to give your answer to the nearest hundredth.

$11.46$

Give your answer clearly with the correct units.

11.46 \, cm^2

Example 6: calculating the area of a semicircle given the diameter

A semicircle has a diameter of $200 \, m.$

Calculate its area.

Give your answer in terms of $\pi.$

Find the radius of the circle.

The question gives you the diameter which is twice the radius.

Diameter $=200 \mathrm{~m}$

Radius $=200 \mathrm{~m} \div 2$

Radius $=100 \mathrm{~m}$

Use the formula $\boldsymbol{\pi} r^2$ to calculate the area of the circle.

\begin{aligned}& \pi r^2 \\\\ &\pi \times r\times r \\\\ &\pi \times100\times 100 \\\\ &10000\pi \end{aligned}

The question asks you to give your answer to ‘in terms of $\pi$ ’. Therefore you leave the answer in the form $10000\pi.$

$10000\pi$

The area of a whole circle with a diameter of $20 \, m.$ You only want the area of a semicircle.

A semicircle has half the area of a full circle so you need to divide your answer by two. Remember to keep it in terms of $\pi.$

$10000\pi \div2$

$5000\pi$

Remember the question asks you to give your answer to ‘in terms of $\pi$ ’. Therefore you leave the answer in the form $5000\pi.$

Give your answer clearly with the correct units.

5000\pi \, m^2

Teaching tips for 𝝅r² (pi r squared)

Encourage students to draw circles, label the radius, and visualize how squaring the radius of the circle $(r^2)$ relates to the circle’s area.

Relate the concept to real-world examples where circles are prevalent, such as pizza, wheels, or clocks. Discuss how understanding the area of a circle is practical in various situations.

Compare the formula for the area of a circle with other area formulas, like the area of a square or parallelogram. Highlight the unique characteristics of circles.

Easy mistakes to make

Not using the radius
You must have the radius to find the area of a circle using the area formula. A question may not give you the radius directly and so you need to use the information given to find the radius first.

Not including the correct units
When working with area, you must always give the correct units squared
For example,
$\mathrm{cm}^2, \mathrm{~m}^2, \mathrm{~km}^2$ etc.

Not rounding correctly
These questions often involve rounding. Only round at the end of the question and to the specified number of decimal places.

Not giving answer in terms of $\boldsymbol{\pi}$
Sometimes the question may ask you to give the answer ‘in terms of $\boldsymbol{\pi}$ ’. This means you do not give the numerical answer that is produced when you multiply it by $\boldsymbol{\pi}.$
For example,
$6 \times \pi=6 \boldsymbol{\pi}$ (this is an answer in terms of pi)
$6 \times \pi=18.8495592 \ldots$ (this answer is not in terms of pi)

Practice pi r squared questions

6 \, cm

3 \, cm

12 \, cm

6\pi \, cm

The diameter of the circle is twice the size of the radius.

Therefore, to find the radius you can divide the diameter by $2.$

12 \mathrm{~cm} \div 2=6 \mathrm{~cm}

\pi d

2\pi r

\pi r^2

\pi r

\pi \times r\times r

Simplify this to,

\text { Area }=\pi r^2

4\pi \, cm^2

4\pi \, cm

12.6 \, cm

12.6 \, cm^2

Area of a circle $=\pi r^2$

$\pi \times 2 \times 2$ is equal to $12.566\dots$

This answer is correctly rounded to the nearest tenth and has the correct units.

9\pi \, cm^2

324\pi \, cm^2

18\pi \, cm^2

81\pi \, cm^2

Area of a circle $=\boldsymbol{\pi} r^2$

\begin{aligned}& \boldsymbol{\pi} \times 9 \times 9 \\\\ & 81 \boldsymbol{\pi} \, cm \end{aligned}

This answer is correctly given in terms of $\boldsymbol{\pi}.$

16\pi \, cm^2

64\pi \, cm^2

8\pi \, cm^2

2\pi \, cm^2

$8 \, cm =$ diameter

$4 \, cm =$ radius

Area of a circle $=\boldsymbol{\pi} r^2$

\begin{aligned}& \pi \times 4 \times 4 \\\\ & 16 \pi \, cm \end{aligned}

This answer is correctly given in terms of $\boldsymbol{\pi}.$

314 \, cm^2

314.1 \, cm^2

314.159 \, cm^2

100\pi \, cm^2

Area of a circle $=\boldsymbol{\pi} r^2$

$\pi \times 10 \times 10$ is equal to $314.1592654\dots$

This answer is correctly rounded to the nearest tenth and has the correct units.

Pi r squared FAQs

What is a circle?

A circle is a shape formed by a curved line; each point on the line is equidistant from the center of the circle.

How do you find the area of circles?

To find the area of circles, use the formula area $A=\boldsymbol{\pi} r^2$ (pi r squared). Area is measured in square units (square meters, square inches, etc.)

Why do we use pi to find the area of circles?

We use pi $(\pi)$ to find the area of circles because it represents the ratio of a circle’s circumference to its diameter. The formula for the area of a circle uses $\pi$ to mathematically relate the size of a circle (measured by its radius $r$ ) to the space it covers.

How can you use the formula $A=\boldsymbol{\pi} r^2$ (pi r squared) to find the radius of a circle?

You can use the formula $A=\boldsymbol{\pi} r^2$ (pi r squared) to find the radius of a circle if you know the area of the circle. Divide area $A$ by $\pi,$ and then find the square root of the quotient.

The next lessons are

Angles of a circle
Circle theorems
Prism shape

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.