Alternate interior angles theorem

Here you will learn about the alternate interior angles theorem, including how to recognize when angles are alternate, and apply this understanding to solve problems.

Students will first learn about the alternate interior angles theorem as part of geometry in 8 th grade.

What is the alternate interior angles theorem?

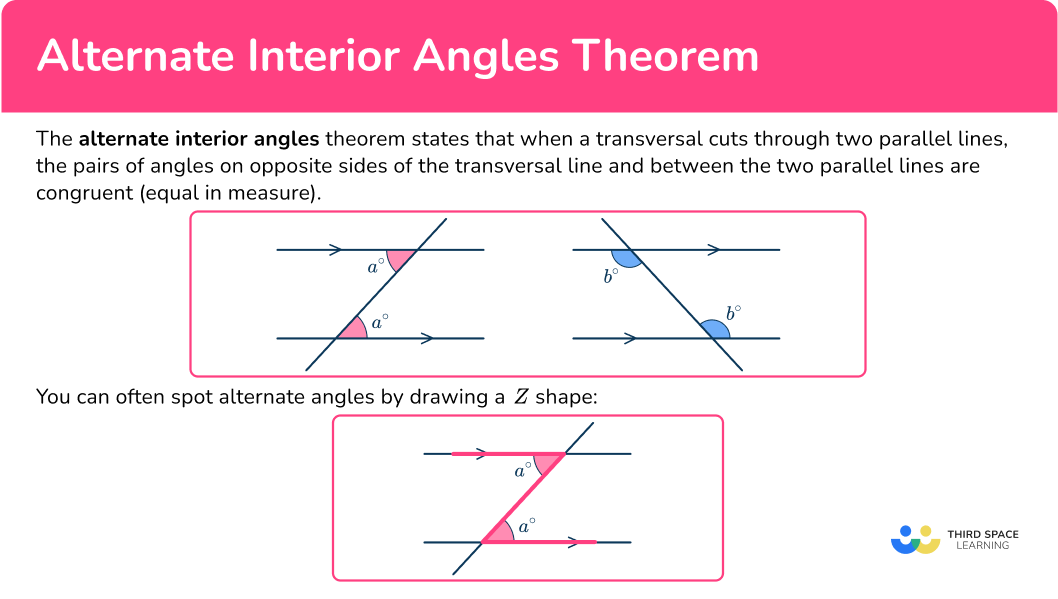
The alternate interior angles theorem states that when a transversal cuts through two parallel lines, the pairs of angles on opposite sides of the transversal line and between the two parallel lines are congruent (equal in measure).

Alternate interior angles are equal

You can often spot alternate angles by drawing a Z shape:

There are two different types of alternate angles: alternate interior angles and alternate exterior angles.

Below are diagrams showing these two variations.

Alternate interior angles

Here, the two angles of a and b are in between the parallel lines and therefore are pairs of alternate interior angles.

Alternate exterior angles

Here, the two angles of c and d are outside of the parallel lines and so these are two examples of pairs of alternate exterior angles.

It is important to notice that the transversal on each diagram is at a different angle but the two angles in each diagram are the same size. As is the case with all diagrams for angles in parallel lines, never use a protractor to find an angle as all the diagrams, unless stated otherwise, are not to scale.

What is the alternate interior angles theorem?

Common Core State Standards

How does this relate to 8 th grade math and high school math?

• Grade 8 – Geometry (8.G.A.5)
  Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.

• High School – Geometry – Congruence (HS.G.CO.C.9)
  Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints.

How to calculate missing angles using the alternate interior angles theorem

In order to calculate missing angles using the alternate interior angles theorem:

1. Highlight the angle(s) that you already know.
2. Use the alternate interior angles theorem to find a missing angle.
3. Use basic angle facts if needed to calculate other missing angles.

Steps 2 and 3 may be done in either order and may need to be repeated.

Step 3 may not always be required.

Alternate interior angles theorem examples

Example 1: alternate interior angles

Calculate the size of the missing angle \theta. Justify your answer.

1. Highlight the angle(s) that you already know.

2Use the alternate interior angles theorem to find a missing angle.

Here you can label the alternate angle on the diagram as 50^{\circ} .

3Use basic angle facts if needed to calculate other missing angles.

Here as \theta is on a straight line with 50^{\circ},

Example 2: alternate interior angles

Calculate the size of the missing angle \theta. Justify your answer.

Highlight the angle(s) that you already know.

Here you can also state the angle 62^{\circ} as it is corresponding to the original angle.

Use the alternate interior angles theorem to find a missing angle.

The angle \theta is the alternate angle to the sum of 56^{\circ} and 62^{\circ} as shown in the given figure.

Example 3: alternate interior angles with algebra

By finding the value for x, calculate the size of the missing angle \theta. Justify your answer.

Highlight the angle(s) that you already know.

Here you know most of the angles, so highlight the angles that are going to help you find the value of x.

Use the alternate interior angles theorem to find a missing angle.

Here, 3x and 30^{\circ} are alternate to each other. You can therefore find the value for x:

\begin{aligned} 3x&=30^{\circ} \\\\ x&=10^{\circ} \end{aligned}

Use basic angle facts if needed to calculate other missing angles.

Here you can use the sum of angles in a triangle to help us calculate the value for \theta.

The value for 10x=100^{\circ} as x=10^{\circ}. You therefore can calculate \theta:

\begin{aligned} \theta&=180^{\circ}-(100^{\circ}+30^{\circ}) \\\\ \theta&=50^{\circ} \end{aligned}

Teaching tips for alternate interior angles theorem

• Have students draw the parallel lines and transversal line, and then color-code pairs of alternate interior angles to make them easy to identify. Ask students to label the angles to help them clearly see which angles are congruent.

• Teach alternate interior angles alongside other types of angle relationships, such as corresponding angles, consecutive interior angles, and supplementary angles, formed by a transversal. This approach helps strengthen students’ overall understanding of angle relationships created by parallel lines.

• To avoid misconceptions, remind students that alternate interior angles are only congruent when the lines are parallel. Create a contrasting example using non-parallel lines to show that alternate interior angles are not necessarily congruent without parallelism.

• Be sure students understand the properties of alternate interior angles:
  • They are located on the inner side of two parallel lines and on opposite sides of the transversal.
  • When the lines are parallel, alternate interior angles are congruent (equal in measure).
  • They help prove parallelism: if alternate interior angles are congruent, then the lines are parallel.

Easy mistakes to make

• Mixing up angles definitions
  There are a lot of angle facts and it is easy to mistake alternate interior angles with corresponding angles or vertically opposite angles. To prevent this from occurring, think about the alternate interior angles being on the alternate sides of the given line.

• Confusing alternate interior angles with linear pairs
  Alternate interior angles are non-adjacent angles between two parallel lines cut by a transversal and are congruent. Linear pair angles are adjacent angles on the same side of the transversal that are supplementary.

• Using a protractor to measure an angle
  Using a protractor to measure an angle. Most diagrams are not to scale and so using a protractor will not result in a correct answer unless it is a coincidence.

Related angles in parallel lines lessons

• Parallel angles
• Corresponding angles
• Same side interior angles

The next lessons are

• 2 D shapes
• Triangles
• Quadrilateral

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.