3D Pythagorean Theorem - Math Steps, Examples & Questions

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Substitution Square roots Solving equations Rounding Congruent shapes 3D shapes Pythagorean theorem

Math resources Geometry Pythagorean theorem

3D Pythagorean theorem

Here you will learn about the 3D Pythagorean theorem including how to apply the Pythagorean theorem in three-dimensional situations.

Students will first learn about the 3D Pythagorean theorem as part of geometry in $8$ th grade (middle school).

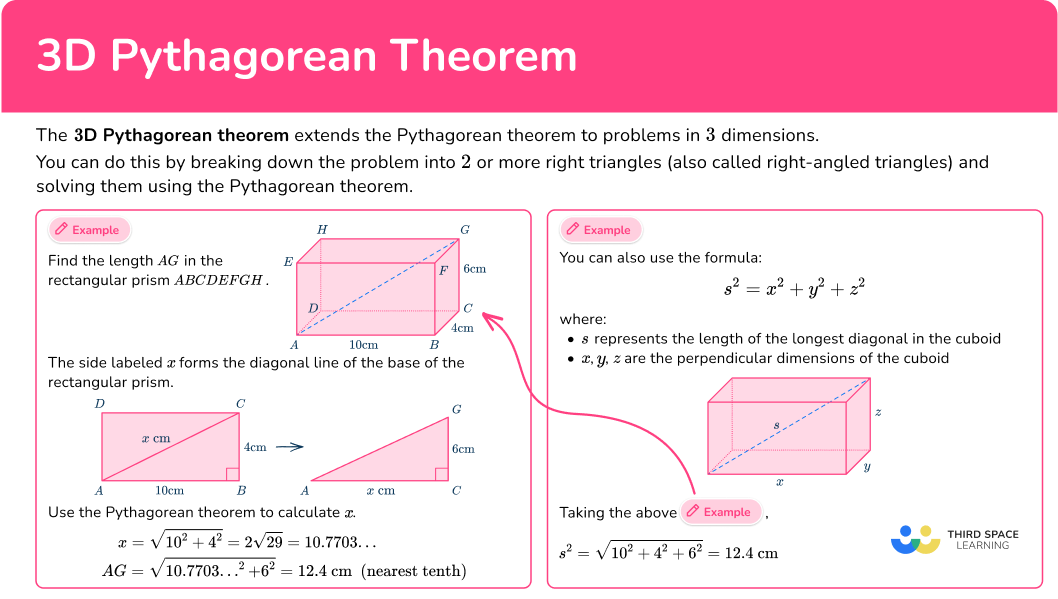
What is the 3D Pythagorean theorem?

The $3$ D Pythagorean theorem extends the Pythagorean theorem to problems in $3$ dimensions.

You can do this by breaking down the problem into $2$ or more right triangles (also called right-angled triangles) and solving them using the Pythagorean theorem.

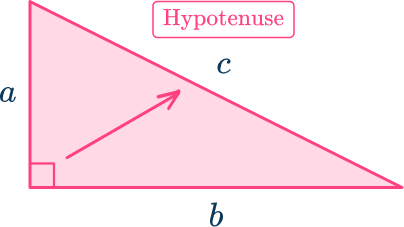
Remember the Pythagorean theorem is $a^2+b^2=c^2$ where $c$ is always the hypotenuse, and $a$ and $b$ are the two shorter, perpendicular sides.

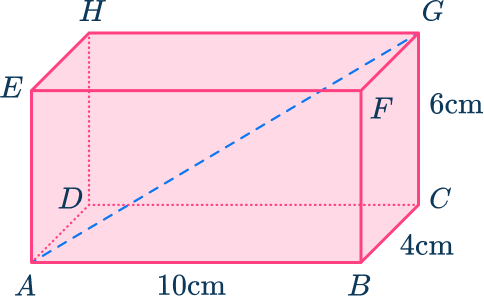
For example, find the length $AG$ in the rectangular prism $ABCDEFGH.$

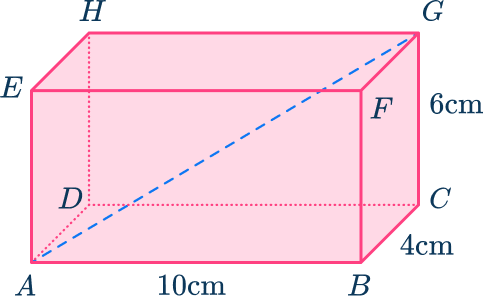
You can make a right triangle $ACG$ which you can use to work out $AG.$

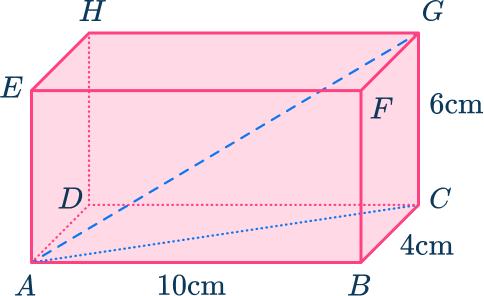
In order to use the Pythagorean theorem, you need to know two sides of the triangle. So in order to work out the longest side $AG,$ you first need to work out one of the shorter sides $AC$ $($ or $EG).$ Here we will look at $AC.$ Let’s call this side $x.$

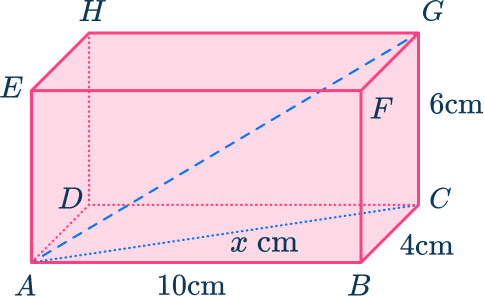
The side labeled $x$ forms the diagonal line of the base of the rectangular prism.

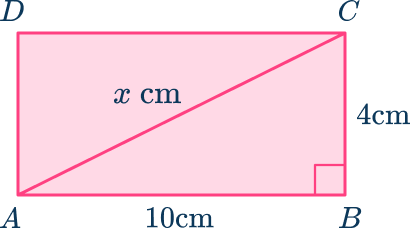
Isolating this triangle from the base of the rectangular prism, you have:

You can see that the triangle $ABC$ is a right triangle, so you can use the Pythagorean theorem to calculate missing side $x.$

x=\sqrt{10^2+4^2}=2\sqrt{29}=10.7703\dots

So, $AG=\sqrt{10.7703…^2+6^2}=\sqrt{152}=2\sqrt{38}=12.328\dots$

So the required length is $12.4\mathrm{~cm}$ (correct to the nearest tenth).

[FREE] Common Core Practice Tests (Grades 3 to 8)

Prepare for math tests in your state with these Grade 3 to Grade 8 practice assessments for Common Core and state equivalents. 40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

DOWNLOAD FREE

[FREE] Common Core Practice Tests (Grades 3 to 8)

DOWNLOAD FREE

3D Pythagorean theorem for rectangular prisms

You can also use a special 3D Pythagorean theorem for rectangular prisms (also known as cuboids) where $x, y, z$ are the sides of a rectangular prism and $s$ is the longest diagonal in the rectangular prism.

s^{2}=x^2+y^2+z^2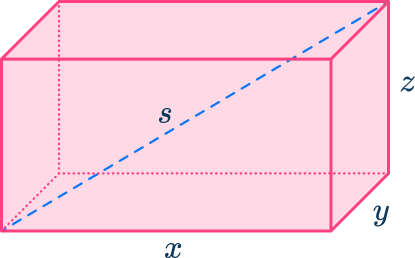

Taking the same example as before,

\begin{aligned} s^2&=10^2+4^2+6^2\\\\s&=\sqrt{10^2+4^2+6^2}\\\\s&=12.4\mathrm{~cm}\text{ (nearest tenth)}\end{aligned}

If angles and lengths are involved in the problem, you may also need to use trigonometry. (This would be seen at the high school level.)

What is the 3D Pythagorean theorem?

Common Core State Standards

How does this relate to $8$ th grade math?

Grade 8 – Geometry (8.G.B.7)
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.

How to solve problems using the 3D Pythagorean theorem

In order to solve problems in three dimensions using the Pythagorean theorem.

Identify the useful right triangle(s).
Apply the Pythagorean theorem.
Finalize your answer.

3D Pythagorean theorem examples

Example 1: cones

Find the slant length of the cone with height $10\mathrm{~cm}$ and radius $8\mathrm{~cm}.$ Give your answer correct to the nearest tenth.

Identify the useful right triangle(s).

You can draw a diagram of the cone and look for the right triangle. The slant length, $l,$ is the hypotenuse of the right triangle with the radius and the height being the adjacent sides to the right angle.

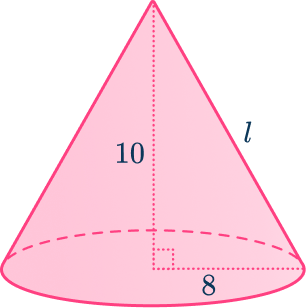
2Apply the Pythagorean theorem.

\begin{aligned}a^2+b^2&=c^2\\\\8^2+10^2&=l^2\\\\l^2&=8^2+10^2\\\\l^2&=64+100\\\\l^2&=164\\\\l&=\sqrt{164}\end{aligned}

3Finalize your answer.

l=\sqrt{164}=12.8062\dots

The slant length of the cone is $12.8\mathrm{~cm}$ (to the nearest tenth).

This is useful as you need the slant length in order to find the curved surface area of a cone.

Example 2: cones

Find the height of the cone with radius $12\mathrm{~cm}$ and slant length $17\mathrm{~cm}.$ Give your answer correct to the nearest tenth.

Identify the useful right triangle(s).

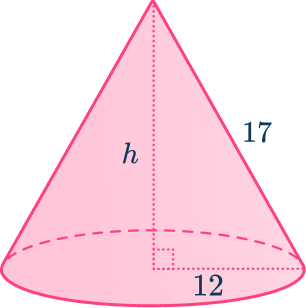
Apply the Pythagorean theorem.

\begin{aligned}a^2+b^2&=c^2\\\\h^2+12^2&=17^2\\\\h^2&=17^2-12^2\\\\h^2&=289-144\\\\h^2&=145\\\\h&=\sqrt{145}\end{aligned}

Finalize your answer.

h = \sqrt{145}=12.04159\dots

The height of the cone is $12.0\mathrm{~cm}$ (to the nearest tenth).

This is useful as you need the height in order to find the volume of a cone.

Example 3: rectangular prism

Here is a rectangular prism $ABCDEFGH.$ Find the length $AG.$ Give your answer correct to the nearest tenth.

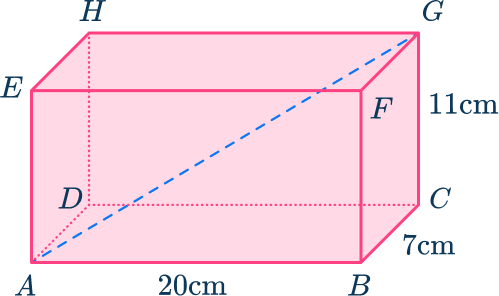
Identify the useful right triangle(s).

Here you need to find the length of $AG.$ As $ACG$ is a right triangle, and you can find the length of $AC$ using the right triangle $ABC,$ the rectangular prism can be broken down into the triangles:

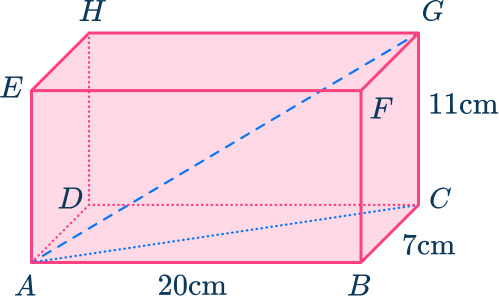
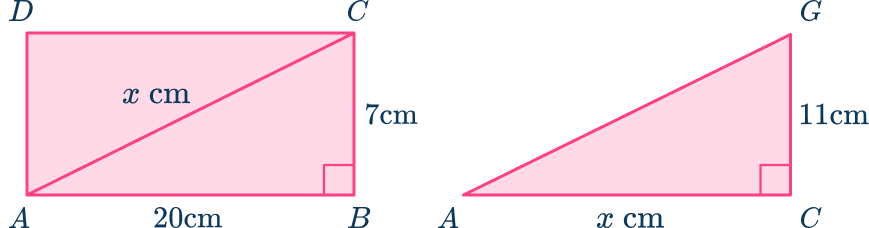
Apply the Pythagorean theorem.

AC=\sqrt{20^2+7^2}=\sqrt{449}=21.1896\dots

So,

$AG=\sqrt{21.1896…^2+11^2}=\sqrt{570}=23.87467\dots$

Finalize your answer.

$AG = \sqrt{570}=23.9\mathrm{~cm}$ (nearest tenth)

Alternatively, you could have done this in one step using $s^{2}=x^2+y^2+z^2:$

$AG=\sqrt{20^2+7^2+11^2}=\sqrt{570}=23.9\mathrm{~cm}$ (nearest tenth)

Example 4: rectangular prism

Here is a rectangular prism $ABCDEFGH.$ Find the length $BH.$ Give your answer correct to the nearest tenth.

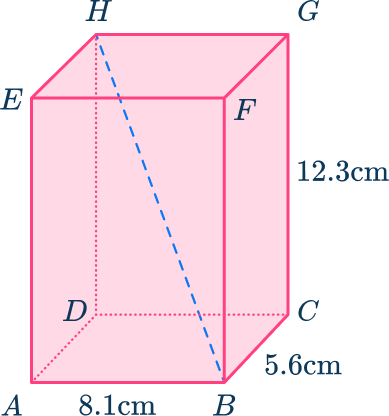
Identify the useful right triangle(s).

Here you need to find the length of $BH.$ As $BDH$ is a right triangle, and you can find the length of $BD$ using the right triangle $ABD,$ the rectangular prism can be broken down into the triangles:

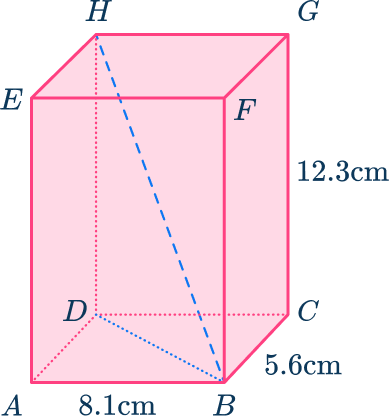
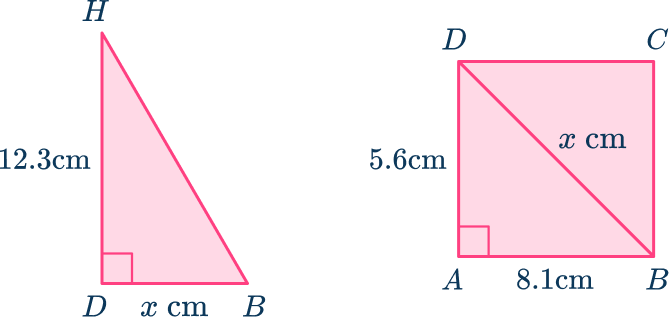
Apply the Pythagorean theorem.

BD=\sqrt{5.6^2+8.1^2} = 9.84733\dots

So,

$BH=\sqrt{9.84733…^2 + 12.3^2} = 15.75626\dots$

Finalize your answer.

$BH=15.8\mathrm{~cm}$ (nearest tenth)

Alternatively, you could have done this in one step:

$BH=\sqrt{8.1^2+5.6^2+12.3^2}=15.8\mathrm{~cm}$

Example 5: pyramids

The diagram shows a square-based pyramid $ABCDX.$

AB=BC=12\mathrm{~cm}

AX=BX=CX=DX=17\mathrm{~cm}

The point $M$ is the midpoint of $AB.$

Calculate the length $MX.$

Give your answer correct to the nearest tenth.

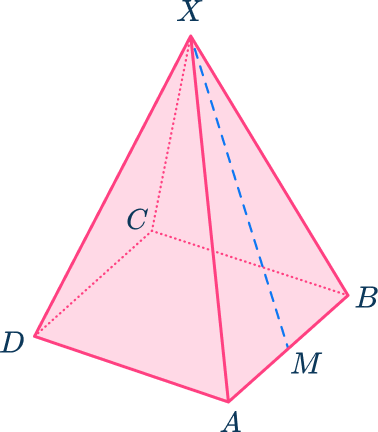
Identify the useful right triangle(s).

Triangle $ABX$ is an isosceles triangle. $MX$ and $AB$ are perpendicular. You can add on the lengths. Remember to halve the length of $AB$ to get the distance of $AM$ and $BM.$

Apply the Pythagorean theorem.

MX=\sqrt{17^2 - 6^2} = 15.90597\dots

Finalize your answer.

$MX=15.9\mathrm{~cm}$ (nearest tenth)

This is useful as you need the height of the triangles in order to find the surface area of a pyramid.

Example 6: pyramids

The diagram shows a square-based pyramid $ABCDX.$

AB=BC=20\mathrm{~cm}

AX=BX=CX=DX=30\mathrm{~cm}

$M$ is the center of the square base $ABCD.$

Calculate the length $MX.$

Give your answer correct to the nearest tenth.

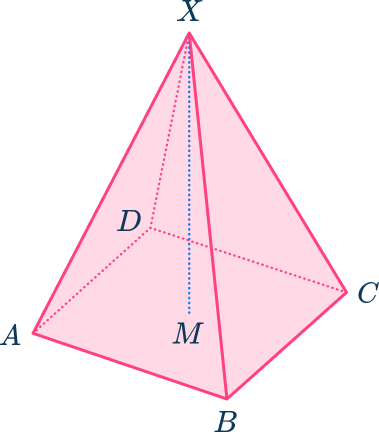
Identify the useful right triangle(s).

Here you need to find the length of $MX.$ As $AMX$ is a right triangle, and you can find the length of $AM$ using the right triangle $ABC,$ the pyramid can be broken down into the triangles:

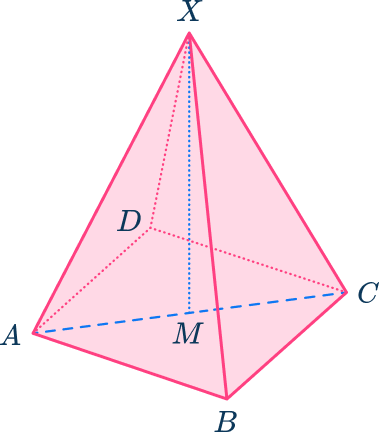
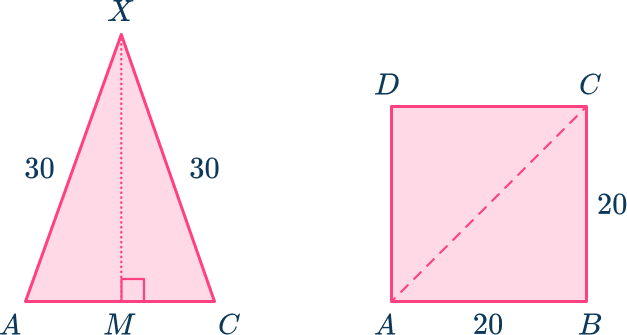
Apply the Pythagorean theorem.

AC=\sqrt{20^2+20^2}=\sqrt{800}=20\sqrt{2}=28.28427\dots

So,

AM=\cfrac{1}{2}AC=10\sqrt{2}=14.14213\dots

$MX=\sqrt{30^2 - 14.14213\dots^2} = 10\sqrt{7} = 26.45751\dots$

Finalize your answer.

$MX=10\sqrt{7}=26.5\mathrm{~cm}$ (nearest tenth)

This is useful as you need the height of the pyramid in order to find the volume of a pyramid.

Teaching tips for 3D Pythagorean theorem

Review the $2$ dimensional Pythagorean theorem. Connect the 2D concept to real-world examples like finding the length of the diagonal of a rectangle before using it with $3$ dimensional shapes.

Include word problems in worksheets that involve real-life scenarios, such as calculating the diagonal of a box, the distance between two points in 3D space, or the length of a ladder leaning against a building.

In worksheets, ask students to calculate unknown lengths of real-life objects, such as the diagonal of a room or a TV screen. Encourage them to recognize that these problems involve right triangles, where line segments represent the sides of a right triangle that form diagonals.

Easy mistakes to make

Thinking three dimensions can’t be difficult to visualize
It can be tricky to identify where right angles are on a 2D diagram of a 3D problem. You may find it useful to get a box to help you to visualize it, such as an old tissue box or a shoe box.

Thinking lengths of sides have to be whole numbers
Lengths can be decimals, fractions or even irrational numbers such as square roots $(\sqrt{2}).$

Rounding too early
If you need to use Pythagoras’ Theorem in a question with multiple steps, do not round until the very end of the question or you will lose accuracy.

Pythagorean theorem

Practice 3D Pythagorean theorem questions

18.1\mathrm{~cm}

11.2\mathrm{~cm}

11.1\mathrm{~cm}

18.0\mathrm{~cm}

3D Pythagorean theorem 22 US

$l=\sqrt{15^2 + 10^2}=18.0\mathrm{~cm}$ (nearest tenth)

12.9\mathrm{~cm}

13.0\mathrm{~cm}

29.8\mathrm{~cm}

29.9\mathrm{~cm}

3D Pythagorean theorem 23 US

$l=\sqrt{23^2 – 19^2}=13.0\mathrm{~cm}$ (nearest tenth)

13.1\mathrm{~cm}

12.4\mathrm{~cm}

13.2\mathrm{~cm}

12.5\mathrm{~cm}

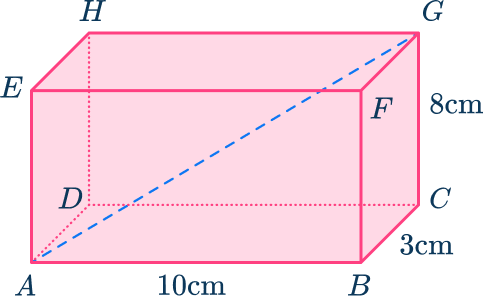
$AG=\sqrt{10^2 + 3^2 + 8^2}=\sqrt{173}=13.2\mathrm{~cm}$ (nearest tenth)

20.2 \mathrm{~cm}

20.3 \mathrm{~cm}

12.4 \mathrm{~cm}

12.5 \mathrm{~cm}

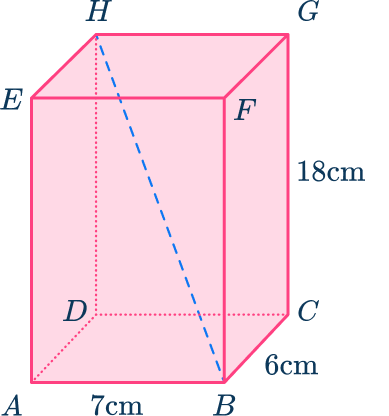
$BH=\sqrt{7^2 + 6^2 + 18^2}=\sqrt{409}=20.2\mathrm{~cm}$ (nearest tenth)

17.2\mathrm{~cm}

14.9\mathrm{~cm}

15.0\mathrm{~cm}

17.3\mathrm{~cm}

AM=AB\div{2}=10\div{2}=5

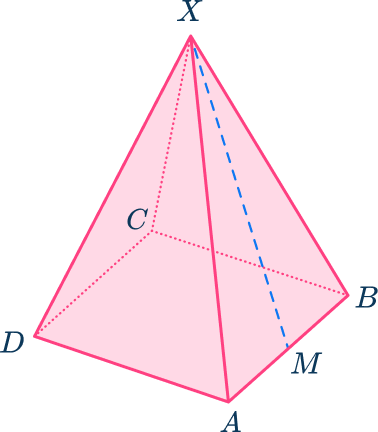
$MX=\sqrt{18^2 – 5^2}=\sqrt{299}=17.3\mathrm{~cm}$ (nearest tenth)

41.3\mathrm{~cm}

41.2\mathrm{~cm}

26.5\mathrm{~cm}

26.4\mathrm{~cm}

AC=\sqrt{40^2 + 40^2} =\sqrt{3200} = 40\sqrt{2}=56.56854\dots

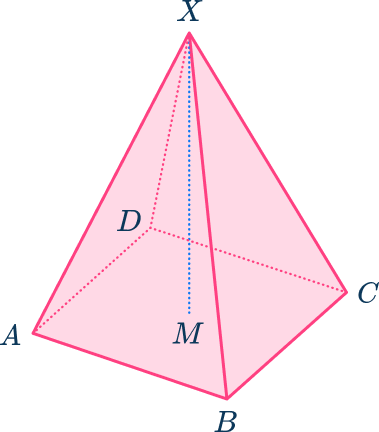
So,

AM=\cfrac{1}{2}AC=20\sqrt{2}=28.28427\dots

$MX=\sqrt{50^2 – 28.28427\dots^2} = 10\sqrt{17} = 41.2\mathrm{~cm}$ (nearest tenth)

3D Pythagorean theorem FAQs

What is the 3D Pythagorean theorem?

The 3D Pythagorean theorem is an extension of the 2D Pythagorean theorem that helps us find the diagonal length of a rectangular prism (a box) using its three dimensions (length, width, and height).

When do I use the 3D Pythagorean theorem?

You use it when you need to find the diagonal length of a rectangular prism or the distance between two points in 3D space.

Can I use the 3D Pythagorean theorem with other shapes?

While it is mainly used for rectangular prisms, you can also apply it to other shapes as long as you can break them down into right triangles or use the dimensions properly.

For example, in a triangular prism, you can apply the theorem to find the diagonal connecting opposite corners by breaking it down into right triangles formed by the height of the prism and the dimensions of the triangular base.

The next lessons are

Trigonometry
Circle math
Sectors arcs and segments

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.