Nonlinear System of Equations - Math Steps, Examples & More!

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Request a demo

In order to access this I need to be confident with:

Rearranging equations Expanding expressions Solving systems of equations by graphing Quadratic equations Quadratic formula

Math resources Algebra System of equations

Nonlinear system of equations

Here you will learn about a nonlinear system of equations, including what they are and how to solve them.

Students will first learn about a nonlinear system of equations as part of algebra in high school.

What is a nonlinear system of equations?

A nonlinear system of equations is two or more equations that form a system, where at least one equation is nonlinear.

One example of a nonlinear equation is a quadratic equation, which has variables that are raised to powers of $2,$ for example, $x^2$ and $y^2.$

There are other types of nonlinear equations, but this page will cover simple systems that involve a linear and a quadratic equation.

One key difference of a nonlinear system of equations compared to linear system of equations is that you can expect multiple answers. This is because of the way the graphs of linear and quadratic functions can intersect.

On the graph below, the straight line of the linear equation crosses the curved parabola of the quadratic equation at two points of intersection.

This means the system of equations has two valid answers.

This is an example of a nonlinear system of equations:

$y=x^{2}-4$ (quadratic)

$y=x+2$ (linear)

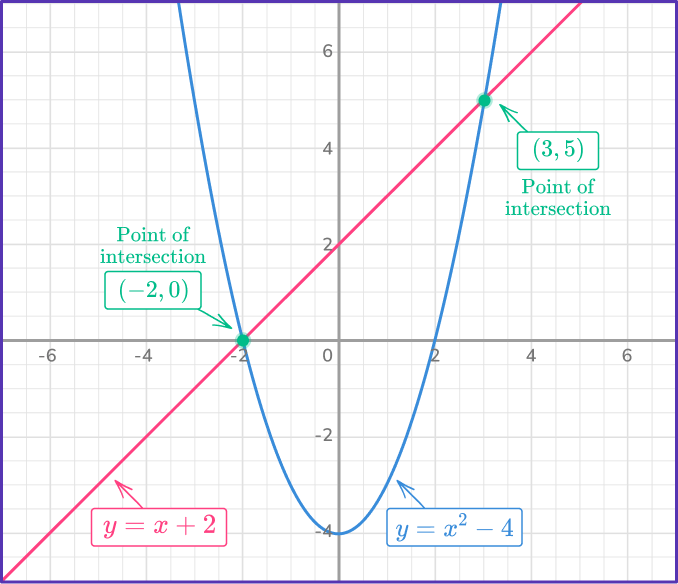
Nonlinear System of Equations Image 1 US

These points of intersection are the solutions to the system of equations. They are ordered pairs that satisfy all equations in the system.

Here, the solutions are $x=3, \, y=5$ and $x=- \, 2, \, y=0.$ This can also be written as a coordinate pair $(3, \, 5)$ and $(- \, 2, \, 0).$

What is a Nonlinear System of Equations?

Common Core State Standards

How does this relate to high school math?

Algebra – Reasoning with Equations and Inequalities (HS.A.REI.C.7)
Solve a simple system consisting of a linear equation and a quadratic equation in two variables algebraically and graphically. For example, find the points of intersection between the line $y=- \, 3x$ and the circle $x^{2}+y^{2}=3.$

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of algebra. 10+ questions with answers covering a range of 6th and 8th grade algebra topics to identify areas of strength and support!

DOWNLOAD FREE

[FREE] Algebra Check for Understanding Quiz (Grade 6 to 8)

DOWNLOAD FREE

How to solve nonlinear system of equations

To solve a set of system of equations you need to:

Use substitution to eliminate one of the variables.
Solve for the value(s) of one variable.
Use substitution to find the value(s) of the remaining variable.
Clearly state the final answer(s).
Check your answer by substituting both values into either of the original equations.

Nonlinear system of equations examples

Example 1: equation of a straight line and a quadratic (factor)

Solve:

\begin{aligned}y&=x+3 \\\\ y&=x^{2}+5x-2 \end{aligned}

Use substitution to eliminate one of the variables.

Use the fact that $y=x+3$ to substitute the value of $y$ into the second equation.

\begin{aligned}y&=x+3 \\\\ y&=x^{2}+5x-2 \end{aligned}

Therefore $x+3=x^{2}+5x-2.$

Another way to think about this is that as both equations are equal to $y,$ they must therefore be equal to one another.

2Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

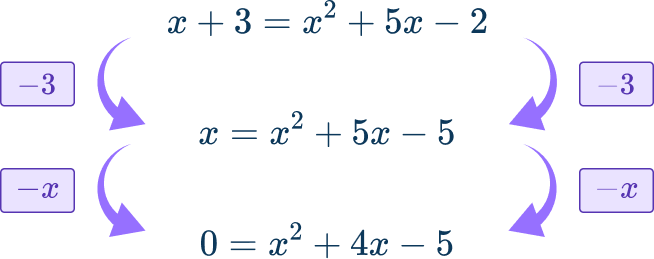
Nonlinear System of Equations Image 2 US

$x^{2}+4x-5=0$ can be factored:

(x+5)(x-1)=0

$x+5=0$ so $x=- \, 5$

$x-1=0$ so $x=1$

The two values of $x$ are $x=- \, 5$ and $x=1.$

3Use substitution to find the value(s) of the remaining variable.

The two values of $x$ can be substituted into one of the original equations to find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

As $y=x+3,$ when $x=- \, 5, \, y=- \, 5+3=- \, 2.$

As $y=x+3,$ when $x=1, \, y=1+3=4.$

4Clearly state the final answer(s).

$x=- \, 5, \, y=- \, 2$ and $x=1, \, y=4.$

5Check your answer by substituting both values into either of the original equations.

Let’s use the quadratic equation to check the answers.

As $y=x^{2}+5x-2,$ when $x=- \, 5,$

\begin{aligned}y&=(- \, 5)^{2}+5(- \, 5)-2 \\\\ &=25-25-2 \\\\ &=- \, 2 \end{aligned}

As $y=x^{2}+5x-2,$ when $x=1,$

\begin{aligned}y&=(1)^{2}+5(1)-2 \\\\ &=1+5-2 \\\\ &=4 \end{aligned}

Both are valid so the answers are correct.

Let’s look at the graph of the system.

\begin{aligned}y&=x+3 \\\\ y&=x^{2}+5x-2 \end{aligned}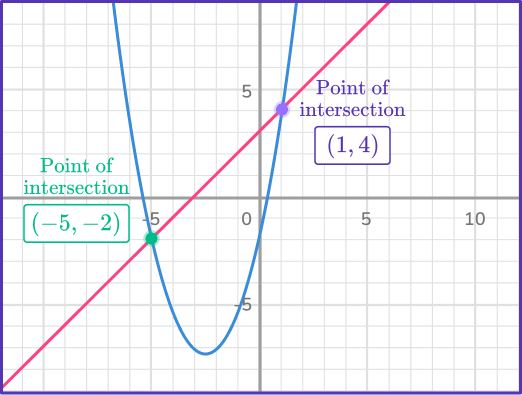

Nonlinear System of Equations Image 3 US

When graphed, these two equations intersect at $(– \, 5, \, – \, 2)$ and $(1, \, 4).$ So the solutions to the system of equations are:

x=- \, 5, \, y=- \, 2

and

x=1, \, y=4

Example 2: equation of a straight line and a quadratic (factor)

Solve:

\begin{aligned}y&=3x-12 \\\\ y&=x^{2}-2x-6 \end{aligned}

Use substitution to eliminate one of the variables.

Use the fact that $y=3x-12$ to substitute the value of $y$ into the second equation.

$\begin{aligned}y&=3x-12 \\\\ y&=x^{2}-2x-6 \end{aligned}$

Therefore $3x-12=x^{2}-2x-6.$

Another way to think about this is that as both equations are equal to $y,$ they must therefore be equal to one another.

Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

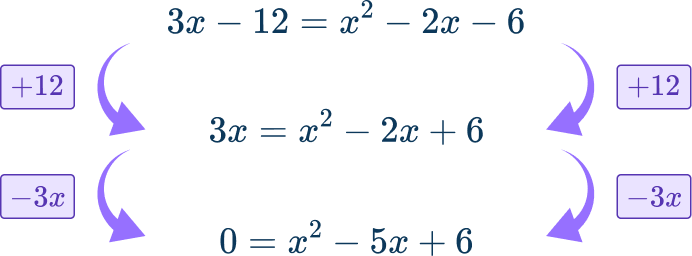
Nonlinear System of Equations Image 4 US

$x^{2}-5x+6=0$ can be factored:

$(x-3)(x-2)=0$

$x-3=0$ so $x=3$

$x-2=0$ so $x=2$

The two values of $x$ are $x=3$ and $x=2.$

Use substitution to find the value(s) of the remaining variable.

The two values of $x$ can be substituted into one of the original equations to find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

As $y=3x-12,$ when $x=3, \, y=3(3)-12=- \, 3.$

As $y=3x-12,$ when $x=2, \, y=3(2)-12=- \, 6.$

Clearly state the final answer(s).

$x=2, \, y=- \, 6$ and $x=3, \, y=- \, 3.$

Check your answer by substituting both values into either of the original equations.

Let’s use the quadratic equation to check the answers.

As $y=x^{2}-2x-6,$ when $x=3,$

$\begin{aligned}y&=(3)^{2}-2(3)-6 \\\\ &=9-6-6 \\\\ &=- \, 3 \end{aligned}$

As $y=x^{2}-2x-6,$ when $x=2,$

$\begin{aligned}y&=(2)^{2}-2(2)-6 \\\\ &=4-4-6 \\\\ &=- \, 6 \end{aligned}$

Both are valid so the answer is correct.

Let’s look at the graph of the system.

$\begin{aligned}y&=3x-12 \\\\ y&=x^{2}-2x-6 \end{aligned}$

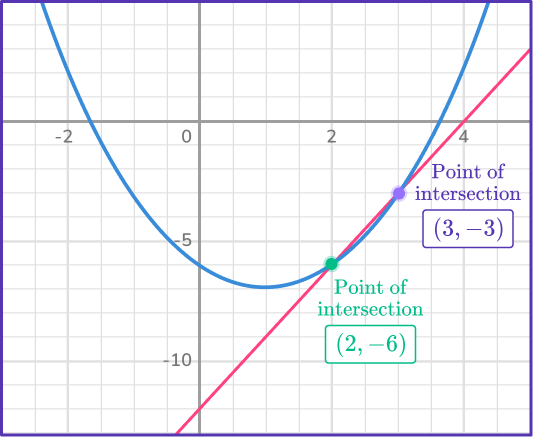
Nonlinear System of Equations Image 5 US

When graphed, these two equations intersect at $(2, \, – \, 6)$ and $(3, \, – \, 3).$ So the solutions to the system of equations are:

$x=2, \, y=- \, 6$ and $x=3, \, y=- \, 3.$

Example 3: equation of a straight line and a circle (factor)

Solve:

\begin{aligned}y^{2}+x^{2}&=29 \\\\ x+7&=y \end{aligned}

Use substitution to eliminate one of the variables.

Use $y=x+7$ to substitute the value of $y$ into the first equation:

$(x+7)^{2}+x^{2}=29$

Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

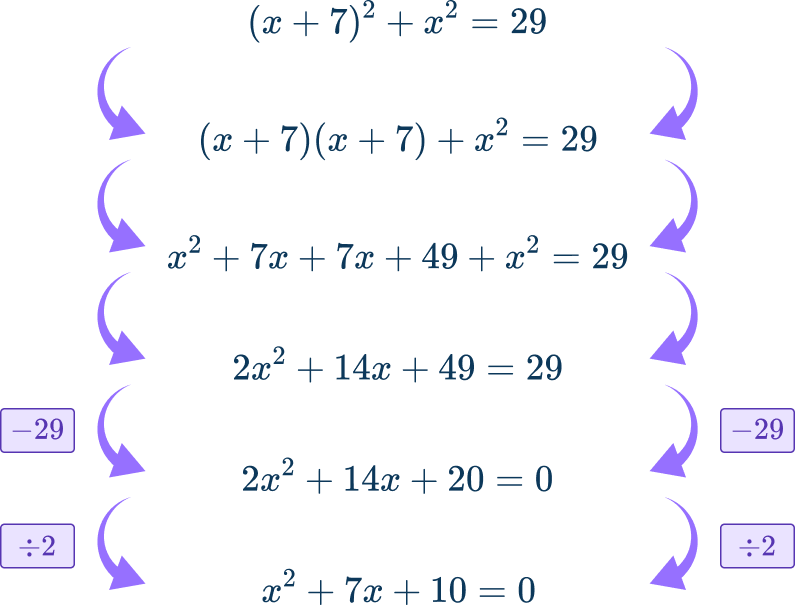
Nonlinear System of Equations Image 6 US

$x^{2}+7x+10=0$ can be factored:

$(x+5)(x+2)=0$

$x+5=0$ so $x=- \, 5$

$x+2=0$ so $x=- \, 2$

The two values of $x$ are $x=- \, 5$ and $x=- \, 2.$

Use substitution to find the value(s) of the remaining variable.

The two values of $x$ can be substituted into one of the original equations to find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

As $x+7=y,$ when $x=- \, 5, \, y=- \, 5+7=2.$

As $x+7=y,$ when $x=- \, 2, \, y=- \, 2+7=5.$

Clearly state the final answer(s).

$x=- \, 5, \, y=2$ and $x=- \, 2, \, y=5.$

Check your answer by substituting both values into either of the original equations.

Let’s use the equation of the circle to check the answers.

Substitute $x=- \, 5, \, y=2$ into $y^2+x^2=29\text{:}$

$2^{2}+(- \, 5)^{2}=4+25=29.$

Substitute $x=- \, 2, \, y=5$ into $y^2+x^2=29\text{:}$

$5^{2}+(- \, 2)^{2}=25+4=29.$

Both are valid so the answers are correct.

Let’s look at the graph of the system:

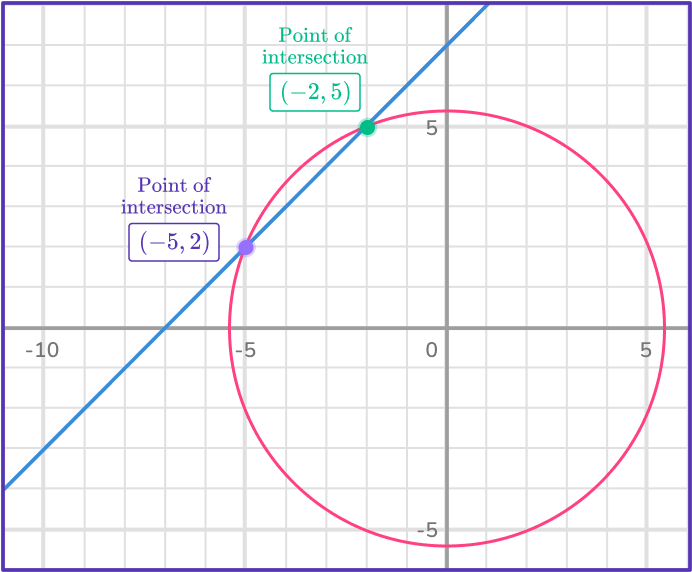
Nonlinear System of Equations Image 7 US

When graphed these two equations intersect at $(– \, 2, \, 5)$ and $(- \, 5, \, 2),$ so the solutions to the system of equations are:

$x=- \, 5, \, y=2$ and $x=- \, 2, \, y=5.$

Notice that the graph of $y^2+x^2=29$ is a circle!

Example 4: equation of a straight line and a circle (quadratic formula)

Solve:

\begin{aligned}y^2+x^2&=14 \\\\ x&=y+2 \end{aligned}

Use substitution to eliminate one of the variables.

Use $x=y+2$ to substitute the value of $x$ into the first equation:

$y^2+(y+2)^2=14$

Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

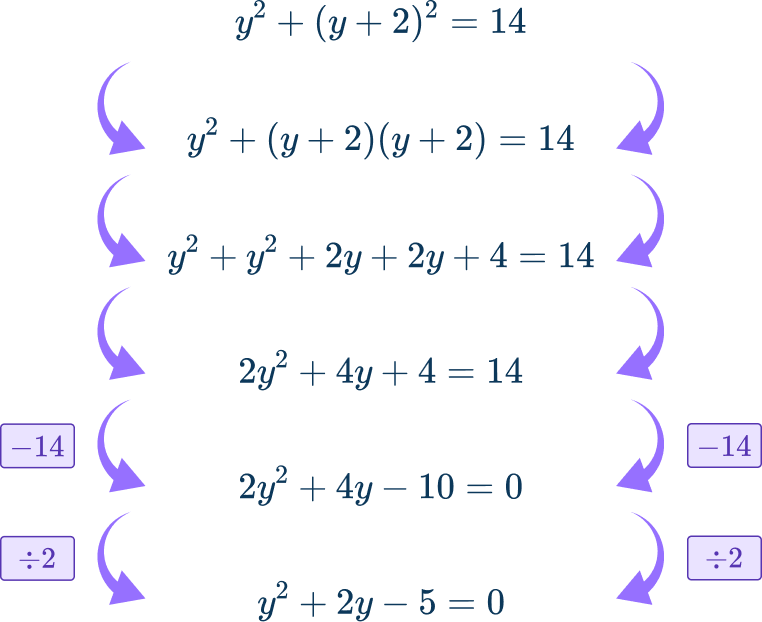
Nonlinear System of Equations Image 8 US

This equation does not factor, so use the quadratic formula to determine the value(s) of $x\text{:}$

$y^{2}+2y-5=0$ with $a=1, \, b=2, \, c=- \, 5$

$\begin{aligned}y&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, 2\pm\sqrt{2^{2}-4(1)(- \, 5)}}{2(1)} \\\\ &=\cfrac{- \, 2\pm\sqrt{4+20}}{2} \\\\ &=\cfrac{- \, 2\pm2\sqrt{6}}{2} \end{aligned}$

$y=- \, 1+\sqrt{6}$ or $y=- \, 1-\sqrt{6}$

Use substitution to find the value(s) of the remaining variable.

The two values of $y$ can be substituted into one of the original equations to find the two possible values of $x.$

Remember you can use either equation, so why not pick the easiest!

As $x=y+2,$ when $y=-1+\sqrt{6}\text{:}$

$x=- \, 1+\sqrt{6}+2=1+\sqrt{6}$

As $x=y+2,$ when $y=- \, 1-\sqrt{6}\text{:}$

$x=- \, 1-\sqrt{6}+2=1-\sqrt{6}$

Clearly state the final answer(s).

\begin{aligned} x&=1+\sqrt{6}, \, \, y=- \, 1+\sqrt{6} \\\\ x&=1-\sqrt{6}, \, \, y=- \, 1-\sqrt{6} \end{aligned}

Check your answer by substituting both values into either of the original equations.

Let’s use the equation of the circle to check the answers.

Substitute $x=1+\sqrt{6},~y=- \, 1+\sqrt{6}$ into $y^{2}+x^{2}=14\text{:}$

$\begin{aligned}&(- \, 1+\sqrt{6})^{2}+(1+\sqrt{6})^{2} \\\\ &=(- \, 1+\sqrt{6})(-1+\sqrt{6})+(1+\sqrt{6})(1+\sqrt{6}) \\\\ &=(1-\sqrt{6}-\sqrt{6}+6)+(1+\sqrt{6}+\sqrt{6}+6) \\\\ &=7-2\sqrt{6}+7+2\sqrt{6} \\\\ &=14. \end{aligned}$

Substitute $x=1-\sqrt{6},~y=- \, 1-\sqrt{6}$ into $y^{2}+x^{2}=14\text{:}$

$\begin{aligned}&(- \, 1-\sqrt{6})^{2}+(1-\sqrt{6})^{2} \\\\ &=(- \, 1-\sqrt{6})(-1-\sqrt{6})+(1-\sqrt{6})(1-\sqrt{6}) \\\\ &=(1+\sqrt{6}+\sqrt{6}+6)+(1-\sqrt{6}-\sqrt{6}+6) \\\\ &=7+2\sqrt{6}+7-2\sqrt{6} \\\\ &=14.\end{aligned}$

Both are valid so the answers are correct.

When graphed these two equations intersect at $(1+\sqrt{6}, \, - \, 1+\sqrt{6})$ and $(1-\sqrt{6}, \, - \, 1-\sqrt{6}),$ so the solutions to the system of equations are:

$x=1+\sqrt{6}, \, y=- \, 1+\sqrt{6}$ and $x=1-\sqrt{6}, \, y=- \,1-\sqrt{6}$

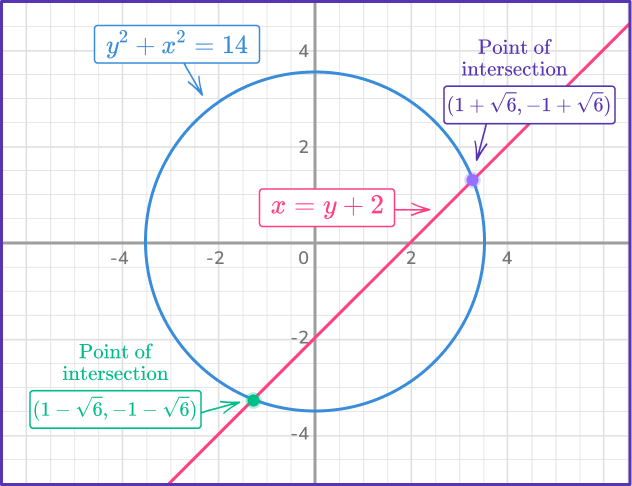
Nonlinear System of Equations Image 9 US

Notice that the graph of $y^2+x^2=14$ is a circle!

Example 5: equation of a straight line and a hyperbola (quadratic formula/factor)

Solve the system of equations:

\begin{aligned}2x^{2}-8y^{2}&=18 \\\\ 3x+4y&=7 \end{aligned}

Use substitution to eliminate one of the variables.

First, make $y$ the subject of the formula in the second equation.

$\begin{aligned}3x+4y&=7 \\\\ 4y&=7-3x \\\\ y&=\cfrac{7-3x}{4} \end{aligned}$

Then, use the fact that $y=\cfrac{7-3x}{4}$ to substitute the value of $y$ into the first equation:

$2x^{2}-8\left(\cfrac{7-3x}{4}\right)^{2}=18.$

Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to 0.

Then solve:

$\begin{aligned}2x^{2}-8\left(\cfrac{7-3x}{4}\right)^{2}&=18 \\\\ 2x^{2}-8\left(\cfrac{7-3x}{4}\right)\left(\cfrac{7-3x}{4}\right)&=18 \\\\ 2x^{2}-8\left(\cfrac{49-21x-21x+9x^{2}}{16}\right)&=18 \\\\ 2x^{2}-8\left(\cfrac{49-42x+9x^{2}}{16}\right)&=18 \\\\ 2x^{2}- \cfrac{49-42x+9x^{2}}{2}&=18 \\\\ 4x^{2}-\left(49-42x+9x^{2}\right)&=36 \\\\ 4x^{2}-49+42x-9x^{2}&=36 \\\\ - \, 49+42x-5x^{2}&=36 \\\\ 42x-5x^{2}&=85 \\\\ - \, 5x^{2}&=- \, 42x+85 \\\\ 0&=5x^{2}-42x+85 \end{aligned}$

This equation appears harder to factor, so use the quadratic formula:

$5x^{2}-42x+85=0$ where $a=5, \, b =- \, 42, \, c= 85$

$\begin{aligned}x&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, (- \, 42)\pm\sqrt{(- \, 42)^{2}-4(5)(85)}}{2(5)} \\\\ &=\cfrac{42\pm\sqrt{1764-1700}}{10} \\\\ &=\cfrac{42\pm\sqrt{64}}{10} \\\\ &=\cfrac{42\pm{8}}{10} \end{aligned}$

$x=3.4$ or $x=5$

Notice that the solutions can be decimals as well as integers.

Use substitution to find the value(s) of the remaining variable.

Since there are two values of $x,$ substitute both values into one of the original equations and find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

As $3x+4y=7,$ when $x=3.4,$

$\begin{aligned}3(3.4)+4y&=7 \\\\ 10.2+4y&=7 \\\\ 4y&=- \, 3.2 \\\\ y&=- \, 0.8 \end{aligned}$

As $3x+4y=7,$ when $x=5,$

$\begin{aligned}3(5)+4y&=7 \\\\ 15+4y&=7 \\\\ 4y&=- \, 8 \\\\ y&=- \, 2 \end{aligned}$

Clearly state the final answer(s).

$x=3.4, \, y=- \, 0.8$ and $x=5, \, y=- \, 2.$

Check your answer by substituting both values into either of the original equations.

As $2x^{2}-8y^{2}=18$ where $x=3.4, \, y=- \, 0.8,$

$2(3.4)^{2}-8(- \, 0.8)^{2}=23.12-5.12=18$

As $2x^{2}-8y^{2}=18$ where $x=5, \, y=- \, 2,$

$2(5)^{2}-8(- \, 2)^{2}=50-32=18$

Both are valid so the answers are correct.

Let’s look at part of the graph of the system.

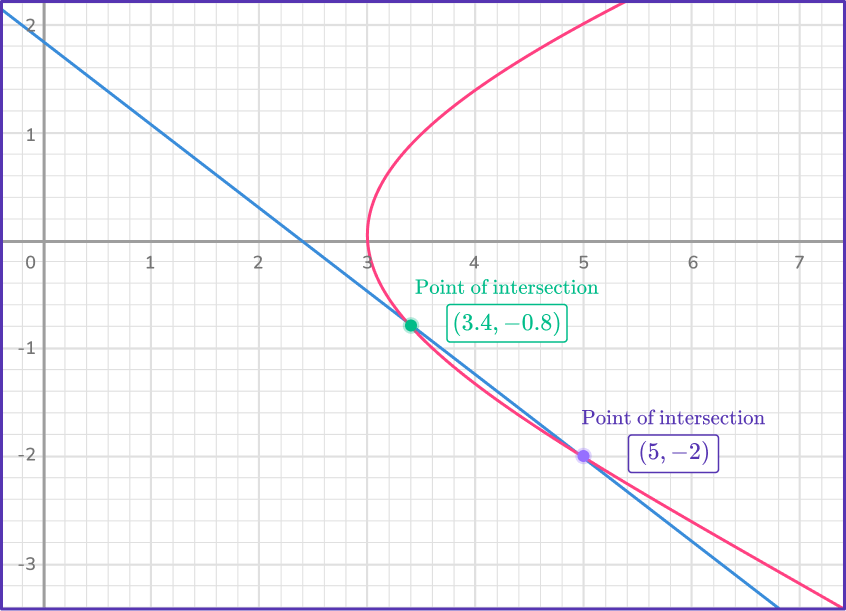
Nonlinear System of Equations Image 10 US

When graphed, these two equations intersect at $(3.4, \, – \,0.8)$ and $(5, \, – \, 2),$ so the solutions to the system of equations are:

$x=3.4, \, y=- \, 0.8$ and $x=5, \, y=- \, 2.$

Example 6: equation of a straight line and an ellipse (quadratic formula)

Solve:

\begin{aligned}x^{2}+8y^{2}&=20 \\\\ 7x+y&=28 \end{aligned}

Use substitution to eliminate one of the variables.

First, make $y$ the subject of the formula in the second equation.

$\begin{aligned}7x+y&=28 \\\\ y&=28-7x \end{aligned}$

Then, use the fact that $y=28-7x$ to substitute the value of $y$ into the first equation:

$x^{2}+8\left(28-7x\right)^{2}=20.$

Solve for the value(s) of one variable.

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

$\begin{aligned}x^{2}+8(28-7x)^{2}&=20 \\\\ x^{2}+8(28-7x)(28-7x)&=20 \\\\ x^{2}+8(784-196x-196x+49x^{2})&=20 \\\\ x^{2}+8(784-392x+49x^{2})&=20 \\\\ x^{2}+6272-3136x+392x^{2}&=20 \\\\ 393x^{2}-3136x+6272&=20 \\\\ 393x^{2}-3136x+6252=0 \end{aligned}$

This equation would be very hard to factor, so use the quadratic formula:

$393x^{2}-3136x+6252=0$ where $a=393, \, b=- \, 3136, \, c=6252$

$\begin{aligned}x&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, (- \, 3136)\pm\sqrt{(- \, 3136)^{2}-4(393)(6252)}}{2(393)} \\\\ &=\cfrac{3136\pm\sqrt{9834496-9828144}}{786} \\\\ &=\cfrac{3136\pm\sqrt{6352}}{786} \\\\ &=\cfrac{3136\pm4\sqrt{397}}{786} \end{aligned}$

$x=4.091220656\dots$ or $x=3.88842311\dots$

Notice that the solutions can be decimals as well as integers.

Use substitution to find the value(s) of the remaining variable.

Since there are two values of $x,$ substitute both values into one of the original equations and find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

As $7x+y=28,$ when $x=4.091 \, (3dp),$

$\begin{aligned}7(4.091)+y&=28. \\\\ 28.637+y&=28 \\\\ y&=- \, 0.637 \end{aligned}$

As $7x+y=28,$ when $x=3.888 \, (3dp),$

$\begin{aligned}7(3.888)+y&=28. \\\\ 27.216+y&=28 \\\\ y&=0.784 \end{aligned}$

Clearly state the final answer(s).

$x=4.091, \, y=- \, 0.637$ and $x=3.888, \, y=0.784.$

Check your answer by substituting both values into either of the original equations.

As $x^{2}+8y^{2}=20$ where $x=4.091, \, y=-0.637,$

$(4.091)^{2}+8(- \, 0.637)^{2}=16.736281+3.246152=20$ (nearest integer)

As $x^{2}+8y^{2}=20$ where $x=3.888, \, y=0.784,$

$(3.888)^{2}+8(0.784)^{2}=15.116544+4.917248=20$ (nearest integer)

Both are valid so the answers are correct.

Let’s look at part of the graph of the system.

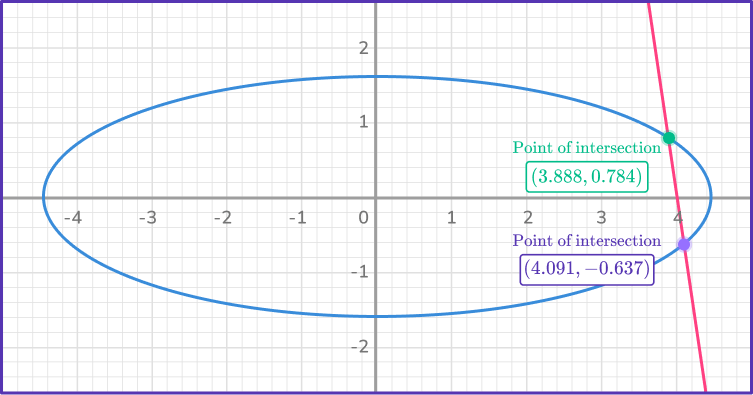
Nonlinear System of Equations Image 11 US

When graphed, these two equations intersect at $(4.091, \, - \, 0.637)$ and $(3.888, \, 0.784),$ so the solutions to the system of equations are:

$x=4.091, \, y=- \, 0.637$ and $x=3.888, \, y=0.784.$

Notice that the graph of $x^{2}+8y^{2}=20$ is an ellipse!

Teaching tips for nonlinear system of equations

Explore systems of linear equations before beginning this topic. It is also a good idea to review skills like changing the subject, operating with square roots and expanding quadratic equations, before asking students to solve systems of nonlinear equations.

Show students a variety of strategies, such as the substitution method or the elimination method, but never require students to solve in a certain way (unless necessary on an assessment). Letting students decide how to solve helps them understand the methods in their own time and allows them to develop analytical skills, such as thinking about which way to solve would be the most efficient.

For students to truly be proficient at solving nonlinear systems, they need to see equations of all kinds, not just equations in standard form.

Easy mistakes to make

Forgetting that squaring a negative number results in a positive
The product of two negative numbers is always positive. It is also important to use parentheses when solving with a calculator to prevent this mistake. See how a calculator solves differently for each type of equation.
For example,

$\begin{aligned}- \, 9^2&=- \, 81 \\\\ \left(- \, 9^2\right)&=81 \\\\ - \, \left(9^2\right)&=- \, 81 \end{aligned}$

Missing solutions
It is easy to forget that a nonlinear system of equations can have two pairs of solutions. Use substitution to find all of the possible solutions.

Substitute $\textbf{y}$ or $\textbf{x}$ incorrectly
A term from the second equation should be isolated, before being used to substitute. Additionally, if the term isolated is $y$ (as is common), then the expression it is equal to should be used as $y$ in the first equation. Not doing this correctly will lead to mistakes.
For example,
The following system $x^{2}-y^{2}=10$ and $y=4x+3$ should be substituted in this way:

$x^{2}-(4x+3)^{2}=10$

Not subtracting the entire term within the parentheses
If a term is being subtracted, all coefficients and constants in the term need to be subtracted.
For example,

$4x^2-\left(49-42x+9x^2\right)=4x^2-49+42x-9x^2$

Not simplifying algebraic fractions
When using algebraic fractions to remove the denominator make sure each term is carefully multiplied. It is much easier to make a mistake when operations involve algebraic fractions.
For example,

$\begin{aligned}&2x^{2}-\cfrac{49-42x+9x^{2}}{2} \\\\ &4x^{2}-(49-42x+9x^{2}) \end{aligned}$

Practice nonlinear system of equations questions

$x=- \, 1, \, y=- \, 2$ and $x=- \, 3, \, y=- \, 2$

$x=1, \, y=2$ and $x=3, \, y=2$

$x=1, \, y=2$ and $x=- \, 3, \, y=- \, 2$

$x=1, \, y=- \, 2$ and $x=3, \, y=- \, 2$

Use the fact that $y=x+1$ to substitute the value of $y$ into the second equation: $x+1=x^{2}+3x-2.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

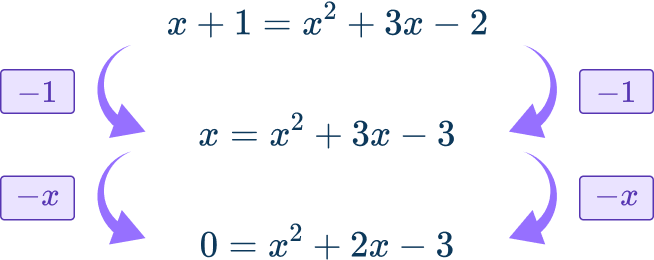
Nonlinear System of Equations Image 12 US

$x^{2}+2x-3=0$ can be factored.

(x+3)(x-1)=0

$x+3=0$ so $x=- \, 3$

$x-1=0$ so $x=1$

The two values of $x$ can be substituted into one of the original equations and find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

When $x=- \, 3, \, \, y=- \, 3+1=- \, 2$

When $x=1, \, y=1+1=2$

The two solutions are $x=- \, 3, \, y=- \, 2$ and $x=1, \, y=2.$

Note: Graph of the system for reference:

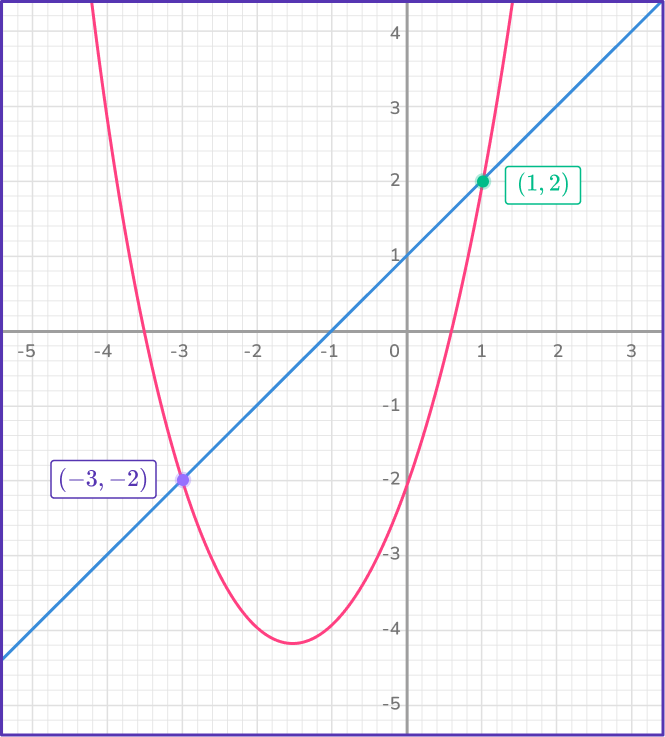
Nonlinear System of Equations Image 13 US

$x=- \, 3, \, y=0$ and $x=0, \, y=- \, 3$

x=3, \, y=0

x=0, \, y=- \, 3

x=- \, 3, \, y=0

Use the fact that $y=x+3$ to substitute the value of $y$ into the second equation: $x+3=x^{2}+7x+12.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

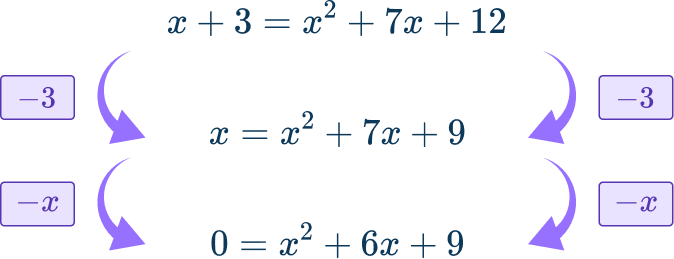
Nonlinear System of Equations Image 14 US

$x^{2}+6x+9=0$ can be factored.

(x+3)(x+3)=0

$x+3=0$ so $x=- \, 3$ only.

The value of $x$ can be substituted into one of the original equations and find the value of $y.$ Note, in this case there is only one solution.

Remember you can use either equation, so why not pick the easiest!

When $x=- \, 3, \, y=- \, 3+3=0$

The solution is $x=- \, 3, \, y=0.$

Note: Graph of the system for reference:

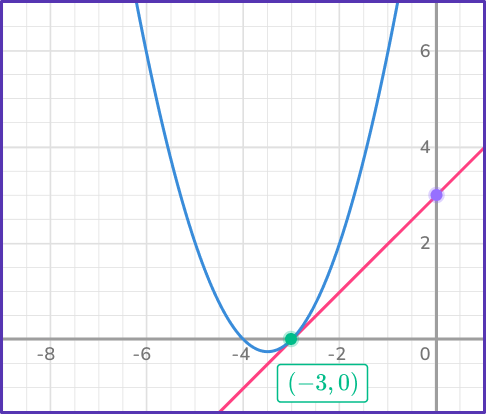
Nonlinear System of Equations Image 15 US

$x=5, \, y=9$ and $x=1, \, y=3$

$x=- \, 5, \, y=9$ and $x=1, \, y=3$

$x=- \, 5, \, y=9$ and $x=- \, 1, \, y=- \, 3$

$x=- \, 5, \, y=9$ and $x=1, \, y=- \, 3$

First, make $y$ the subject of the formula in the second equation.

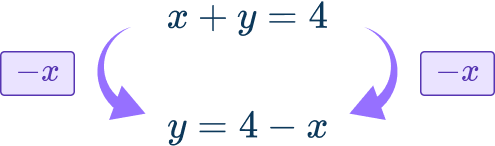
Nonlinear System of Equations Image 16 US

Use the fact that $y=4-x$ to substitute the value of $y$ into the second equation: $4-x=x^{2}+3x-1.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

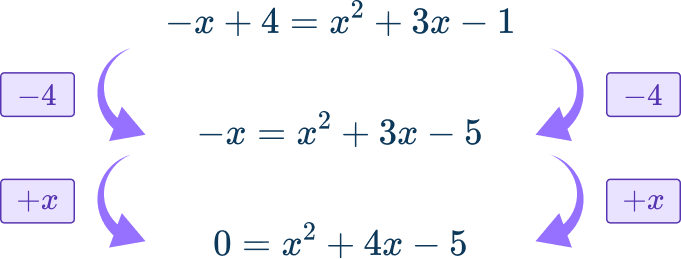
Nonlinear System of Equations Image 17 US

$x^{2}+4x-5=0$ can be factored.

(x+5)(x-1)=0

$x+5=0$ so $x=- \, 5$

$x-1=0$ so $x=1$

The two values of $x$ can be substituted into one of the original equations and find the two possible values of $y.$

When $x=- \, 5, \, – \, 5+y=4$ so $y=9$

When $x=1, \, 1+y=4$ so $y=3$

The two solutions are $x=- \, 5, \, y=9$ and $x=1, \, y=3.$

Note: Graph of the system for reference:

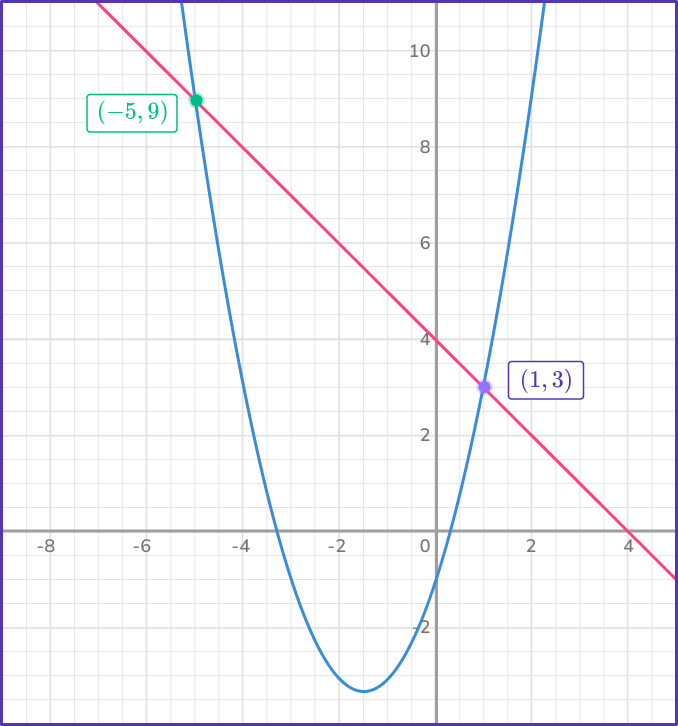
Nonlinear System of Equations Image 18 US

x=- \, \cfrac{1}{3},~y=- \, \cfrac{11}{3}

x=- \, \cfrac{1}{3},~y=\cfrac{11}{3}

x=\cfrac{1}{3},~y=\cfrac{1}{3}

x=\cfrac{1}{3},~y=1

First, make $y$ the subject of the formula in the second equation.

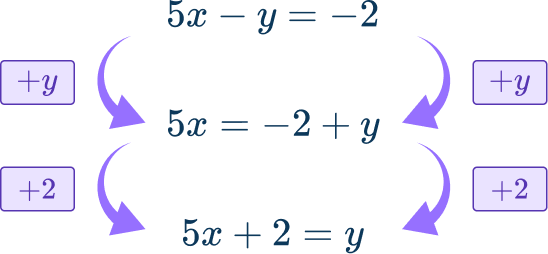
Nonlinear System of Equations Image 19 US

Use the fact that $y=2+5x$ to substitute the value of $y$ into the second equation: $2+5x=9x^2+11x+3.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

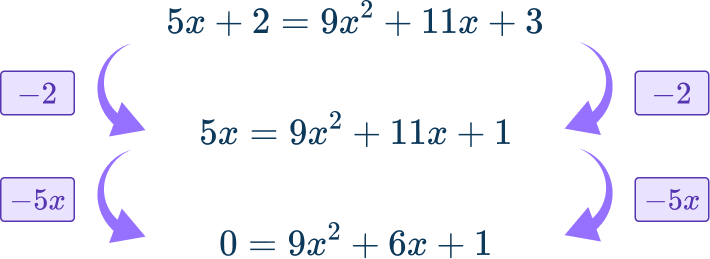
Nonlinear System of Equations Image 20 US

This equations appears harder to factor, so use the quadratic formula:

$9x^{2}+6x+1=0$ where $a=9, \, b=6, \, c=1$

\begin{aligned}x&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, (6)\pm\sqrt{(6)^{2}-4(9)(1)}}{2(9)} \\\\ &=\cfrac{- \, 6\pm\sqrt{36-36}}{18} \\\\ &=\cfrac{- \, 6\pm{0}}{18} \\\\ &=\cfrac{- \, 6}{18} \\\\ &=- \, \cfrac{1}{3} \end{aligned}

$x=- \, \cfrac{1}{3}$ only

The value of $x$ can be substituted into one of the original equations and find the value of $y.$ Note, in this case there is only one solution.

Remember you can use either equation, so why not pick the easiest!

When $x=- \, \cfrac{1}{3},$

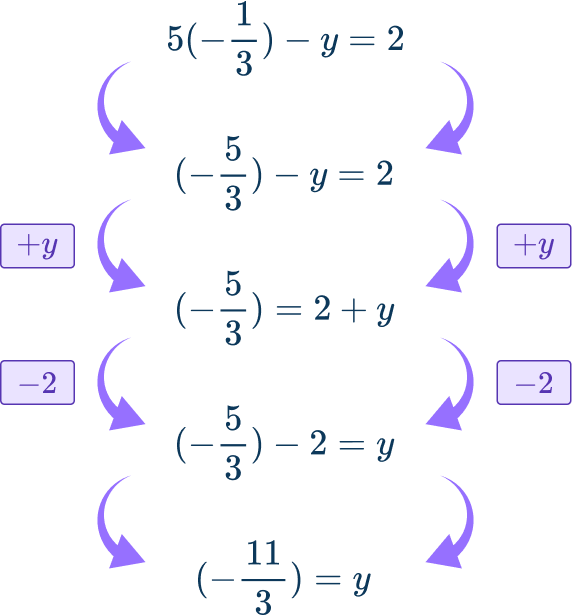
Nonlinear System of Equations Image 21 US

The one solution is $x=- \, \cfrac{1}{3},~y=- \, \cfrac{11}{3}.$

Note: Graph of the system for reference:

Nonlinear System of Equations Image 22 US

$x=1+2\sqrt{3},~y=3+2\sqrt{3}$ and $x=- \, 1+2\sqrt{3},~y=- \, 3+2\sqrt{3}$

$x=- \, 1-2\sqrt{3},~y=- \, 3-2\sqrt{3}$ and $x=1-2\sqrt{3},~y=3-2\sqrt{3}$

$x=1+2\sqrt{3},~y=- \, 3-2\sqrt{3}$ and $x=- \, 1+2\sqrt{3},~y=3-2\sqrt{3}$

$x=- \, 1-2\sqrt{3},~y=- \, 3-2\sqrt{3}$ and $x=- \, 1+2\sqrt{3},~y=- \, 3+2\sqrt{3}$

Use the fact that $y= x-2$ to substitute the value of $y$ into the second equation: $2x^{2}-x(x-2)=11.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

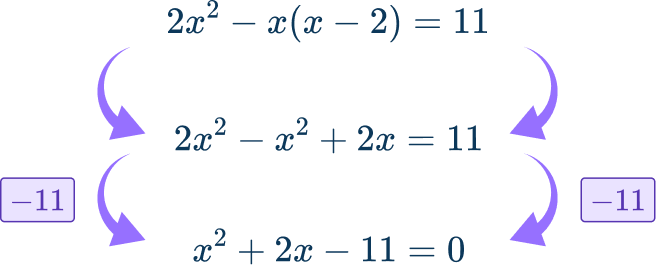
Nonlinear System of Equations Image 23 US

This equations appears harder to factor, so use the quadratic formula:

$x^{2}+2x-11=0$ with $a=1, \, b=2, \, c=- \, 11$

\begin{aligned}x&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, 2\pm\sqrt{2^{2}-4(1)(-11)}}{2(1)} \\\\ &=\cfrac{- \, 2\pm\sqrt{4+44}}{2} \\\\ &=\cfrac{- \, 2\pm\sqrt{48}}{2} \\\\ &=\cfrac{- \, 2\pm4\sqrt{3}}{2} \\\\ &=- \, 1\pm2\sqrt{3} \end{aligned}

$x=- \, 1+2\sqrt{3}$ or $x=- \, 1-2\sqrt{3}$

The two values of $x$ can be substituted into one of the original equations and find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

When $x=- \, 1+2\sqrt{3},$

$y=- \, 1+2\sqrt{3}-2$ so $y=- \, 3+2\sqrt{3}$

When $x=- \, 1-2\sqrt{3},$

$y=- \, 1-2\sqrt{3}-2$ so $y=- \, 3-2\sqrt{3}$

The two solutions are $x=- \, 1+2\sqrt{3},~y=- \, 3+2\sqrt{3}$ and $x=- \, 1-2\sqrt{3},~y=- \, 3-2\sqrt{3}.$

Note: Graph of the system for reference:

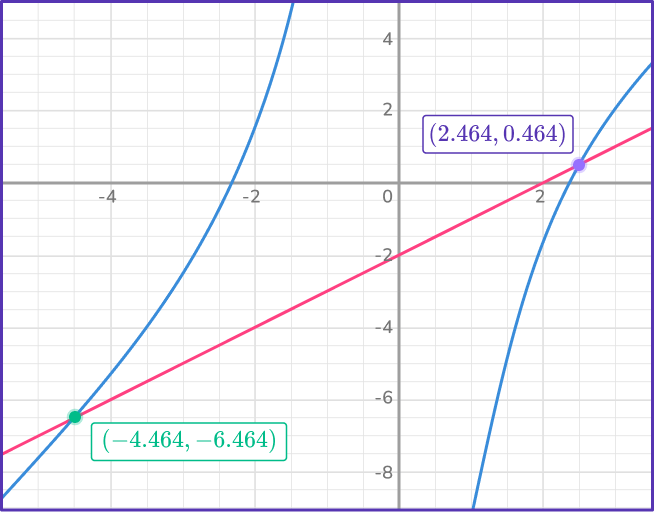
Nonlinear System of Equations Image 24 US

$x=0.5,~y=- \, 0.75$ and $x=- \, 2,~y=- \, 2$

$x=- \, 0.5,~y=- \, 0.75$ and $x=2,~y=- \, 2$

$x=0.5,~y=0.75$ and $x=2,~y=2$

$x=0.5,~y=- \, 0.75$ and $x=2,~y=- \, 2$

First, make $y$ the subject of the formula in the first equation.

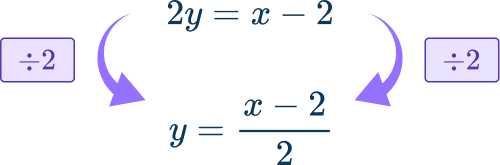
Nonlinear System of Equations Image 25 US

Use the fact that $\cfrac{x-2}{2}$ to substitute the value of $y$ into the second equation: $\cfrac{x-2}{2}=x^{2}+2x-2.$

Since the equation is now quadratic, rearrange so that the equation is equal to $0.$

Then solve:

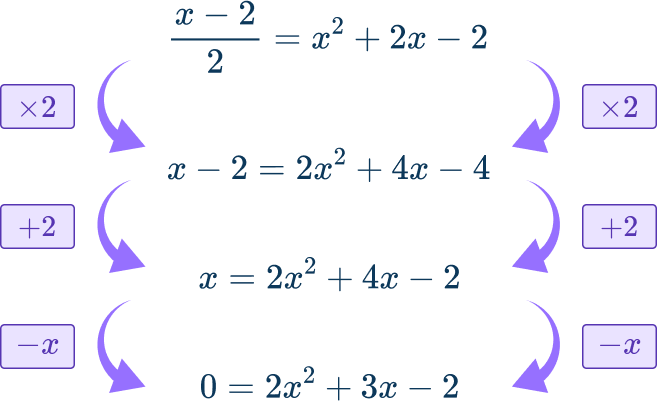
Nonlinear System of Equations Image 26 US

This equations appears harder to factor, so use the quadratic formula:

$2x^{2}+3x-2=0$ with $a=2, \, b=3, \, c=- \, 2$

\begin{aligned}x&=\cfrac{- \, b\pm\sqrt{b^{2}-4ac}}{2a} \\\\ &=\cfrac{- \, 3\pm\sqrt{3^{2}-4(2)(- \, 2)}}{2(2)} \\\\ &=\cfrac{- \, 3\pm\sqrt{9+16}}{4} \\\\ &=\cfrac{- \, 3\pm\sqrt{25}}{4} \\\\ &=\cfrac{- \, 3\pm{5}}{4} \end{aligned}

$x=\cfrac{- \, 3+5}{4}=\cfrac{1}{2}$ or $x=\cfrac{- \, 3-5}{4}=- \, 2$

The two values of $x$ can be substituted into one of the original equations and find the two possible values of $y.$

Remember you can use either equation, so why not pick the easiest!

When $x=\cfrac{1}{2},$

\begin{aligned}2y&=\cfrac{1}{2}-2 \\\\ &=- \, \cfrac{3}{2} \\\\ y&=- \, \cfrac{3}{2}\div{2} \\\\ &=- \, \cfrac{3}{4} \end{aligned}

When $x=- \, 2,$

\begin{aligned}2y&=- \, 2-2 \\\\ &=- \, 4 \\\\ y&=- \, 4\div{2} \\\\ &=- \, 2 \end{aligned}

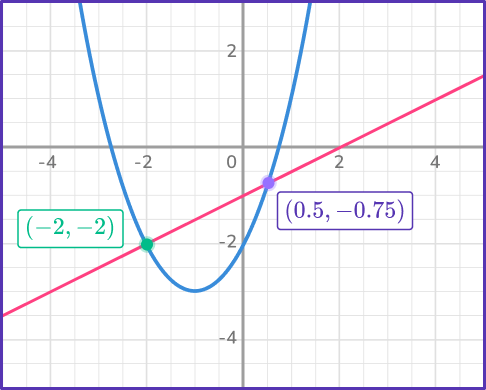
The two solutions are $x=\cfrac{1}{2},~y=- \, \cfrac{3}{4}$ and $x=- \, 2,~y=- \, 2.$

Note: Graph of the system for reference:

Nonlinear System of Equations Image 27 US

Nonlinear systems of equations FAQs

What are linear functions?

Functions that create straight line graphs.

Can exponential equations be part of a nonlinear system of equations?

Yes, any equation can be part of a nonlinear system of equation.

What are polynomials?

A mathematical expression that has variables, coefficients and exponents.

The next lessons are

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.